Type-Driven Development with Idris

Edwin Brady

Copyright

Để biết thông tin trực tuyến và đặt hàng cuốn sách này cũng như các cuốn sách khác của Manning, vui lòng truy cập www.manning.com. Nhà xuất bản cung cấp giảm giá cho cuốn sách này khi đặt hàng số lượng lớn. Để biết thêm thông tin, vui lòng liên hệ.

 Special Sales Department Manning Publications Co. 20 Baldwin Road PO Box 761 Shelter Island, NY 11964 Email: orders@manning.com

Không một phần nào của ấn phẩm này được phép sao chép, lưu trữ trong hệ thống truy xuất, hoặc truyền đạt, dưới bất kỳ hình thức nào hoặc bằng bất kỳ phương tiện nào như điện tử, cơ học, photocopy, hoặc bất kỳ hình thức nào khác, mà không có sự cho phép bằng văn bản trước của nhà xuất bản.

Nhiều trong số các tên gọi được các nhà sản xuất và người bán sử dụng để phân biệt sản phẩm của họ được tuyên bố là nhãn hiệu. Khi những tên gọi đó xuất hiện trong cuốn sách, và Manning Publications biết về một yêu cầu nhãn hiệu, các tên gọi đã được in chữ cái đầu tiên viết hoa hoặc in hoa toàn bộ.

Nhận thức được tầm quan trọng của việc bảo tồn những gì đã được viết, chính sách của Manning là in các cuốn sách chúng tôi xuất bản trên giấy không chua, và chúng tôi nỗ lực hết mình để đạt được mục tiêu đó. Cũng nhận thức được trách nhiệm của chúng tôi trong việc bảo tồn tài nguyên của hành tinh, sách Manning được in trên giấy có ít nhất 15% là giấy tái chế và được xử lý mà không sử dụng clo nguyên tố.

Manning Publications Co. 20 Baldwin Road PO Box 761 Shelter Island, NY 11964

Development editor: Dan Maharry Review editor: Aleksandar Dragosavljević Technical development editor: Andrew Gibson Project editor: Kevin Sullivan Copyeditor: Andy Carroll Proofreader: Katie Tennant Technical proofreaders: Arnaud Bailly, Nicolas Biri Typesetter: Dottie Marsico Cover designer: Marija Tudor

ISBN 9781617293023

In ấn tại Hoa Kỳ

1 2 3 4 5 6 7 8 9 10 – EBM – 22 21 20 19 18 17

Brief Table of Contents

Bản quyền

Mục lục ngắn gọn

Mục lục

Lời nói đầu

Lời cảm ơn

Về cuốn sách này

Về tác giả

Về hình minh họa bìa

1. Giới thiệu

Chương 1. Tổng quan

Chương 2. Bắt đầu với Idris

2. Idris cốt lõi

Chương 3. Phát triển tương tác với kiểu dữ liệu

Chương 4. Kiểu dữ liệu do người dùng định nghĩa

Chương 5. Chương trình tương tác: xử lý đầu vào và đầu ra

Chương 6. Lập trình với các kiểu hạng nhất

Chương 7. Giao diện: sử dụng kiểu tổng quát bị ràng buộc

Chương 8. Sự bình đẳng: biểu thị mối quan hệ giữa các dữ liệu

Chương 9. Các predicate: diễn đạt giả định và hợp đồng trong loại.

Chương 10. Quan điểm: mở rộng khớp mẫu

3. Idris và thế giới thực

Chương 11. Dòng dữ liệu và quy trình: làm việc với dữ liệu vô hạn

Chương 12. Viết chương trình với trạng thái

Chương 13. Máy trạng thái: xác minh giao thức trong kiểu dữ liệu

Chương 14. Các máy trạng thái phụ thuộc: xử lý phản hồi và lỗi

Chương 15. Lập trình đồng thời an toàn kiểu dữ liệu

Phụ lục A. Cài đặt Idris và chế độ chỉnh sửa

Phụ lục B. Các lệnh chỉnh sửa tương tác

Phụ lục C. Lệnh REPL

Phụ lục D. Tài liệu tham khảo thêm

Phụ lục

Phụ lục

Chỉ mục

Danh sách hình ảnh

Danh sách bảng

Danh sách niêm yết

Bản quyền

Mục lục ngắn gọn

Mục lục

Lời nói đầu

Lời cảm ơn

Về cuốn sách này

Về tác giả

Về minh họa bìa

1. Giới thiệu

Chương 1. Tổng quan

1.1. Kiểu là gì?

1.2. Giới thiệu phát triển dựa trên kiểu dữ liệu

1.2.1. Đại số ma trận

1.2.2. Một máy rút tiền tự động

1.2.3. Lập trình đồng thời

1.2.4. Loại, định nghĩa, tinh chỉnh: quy trình phát triển dựa trên kiểu dữ liệu

1.2.5. Kiểu phụ thuộc

1.3. Lập trình hàm thuần túy

1.3.1. Tính tinh khiết và tính trong suốt tham chiếu

1.3.2. Chương trình có tác dụng phụ

1.3.3. Hàm riêng phần và hàm toàn phần

1.4. Một chuyến tham quan nhanh về Idris

1.4.1. Môi trường tương tác

1.4.2. Kiểm tra kiểu dữ liệu

1.4.3. Biên dịch và chạy các chương trình Idris

1.4.4. Định nghĩa không đầy đủ: làm việc với những khoảng trống

1.4.5. Kiểu hạng nhất

1.5. Tóm tắt

Chương 2. Bắt đầu với Idris

2.1. Các loại cơ bản

2.1.1. Các kiểu và giá trị số

2.1.2. Chuyển đổi kiểu dữ liệu bằng cách sử dụng ép kiểu

2.1.3. Ký tự và chuỗi

2.1.4. Kiểu dữ liệu Boolean

2.2. Hàm: những khối xây dựng của các chương trình Idris

2.2.1. Các loại hàm và định nghĩa

2.2.2. Áp dụng một phần các hàm

2.2.3. Viết hàm tổng quát: biến trong kiểu dữ liệu

2.2.4. Viết các hàm tổng quát với kiểu dữ liệu ràng buộc

2.2.5. Các loại hàm bậc cao

2.2.6. Hàm ẩn danh

2.2.7. Định nghĩa cục bộ: let và where

2.3. Loại tổng hợp

2.3.1. Cặp giá trị

2.3.2. Danh sách

2.3.3. Hàm với danh sách

Một chương trình Idris hoàn chỉnh

2.4.1. Ý nghĩa của khoảng trắng: quy tắc bố cục

2.4.2. Bình luận tài liệu

2.4.3. Chương trình tương tác

2.5. Tóm tắt

2. Idris cốt lõi

Chương 3. Phát triển tương tác với kiểu dữ liệu

3.1. Chỉnh sửa tương tác trong Atom

3.1.1. Tóm tắt lệnh tương tác

3.1.2. Định nghĩa hàm bằng cách khớp mẫu

3.1.3. Các loại dữ liệu và mẫu

3.2. Thêm độ chính xác cho các kiểu: làm việc với các vectơ

3.2.1. Tinh chỉnh loại của allLengths

3.2.2. Tìm kiếm theo kiểu: tinh chỉnh tự động

3.2.3. Loại, định nghĩa, hoàn thiện: sắp xếp một vector

3.3. Ví dụ: phát triển dựa trên kiểu cho các hàm ma trận

3.3.1. Các phép toán ma trận và các loại của chúng

3.3.2. Chuyển vị một ma trận

3.4. Tham số ngầm định: biến cấp độ kiểu

3.4.1. Sự cần thiết của các tham số ngầm định

3.4.2. Ngụ ý ràng buộc và không ràng buộc

3.4.3. Sử dụng tham số ngầm trong các hàm

3.5. Tóm tắt

Chương 4. Các kiểu dữ liệu do người dùng xác định

4.1. Định nghĩa các kiểu dữ liệu

4.1.1. Liệt kê

4.1.2. Loại kết hợp

4.1.3. Các kiểu đệ quy

4.1.4. Các kiểu dữ liệu tổng quát

4.2. Định nghĩa các loại dữ liệu phụ thuộc

4.2.1. Một ví dụ đầu tiên: phân loại phương tiện theo nguồn năng lượng

4.2.2. Định nghĩa vector

4.2.3. Lập chỉ mục các vector bằng các số có giới hạn sử dụng Fin

4.3. Triển khai dựa trên kiểu cho một kho dữ liệu tương tác

4.3.1. Đại diện cho cửa hàng

4.3.2. Duy trì trạng thái tương tác trong hàm main

4.3.3. Lệnh: phân tích đầu vào của người dùng

4.3.4. Xử lý lệnh

4.4. Tóm tắt

Chương 5. Chương trình tương tác: xử lý đầu vào và đầu ra

5.1. Lập trình tương tác với IO

5.1.1. Đánh giá và thực hiện các chương trình tương tác

5.1.2. Hành động và tuần tự: toán tử >>=

5.1.3. Đường cú pháp cho việc xắp xếp với chú thích do

5.2. Chương trình tương tác và luồng điều khiển

5.2.1. Tạo ra các giá trị thuần khiếm trong các định nghĩa tương tác

5.2.2. Ràng buộc khớp mẫu

5.2.3. Viết định nghĩa tương tác với vòng lặp

5.3. Đọc và xác thực các loại phụ thuộc

5.3.1. Đọc một Vect từ bảng điều khiển

5.3.2. Đọc một Vect có chiều dài không xác định

5.3.3. Các cặp phụ thuộc

5.3.4. Xác thực độ dài của Vect

5.4. Tóm tắt

Chương 6. Lập trình với kiểu dữ liệu hạng nhất

6.1. Hàm cấp loại: tính toán kiểu

6.1.1. Từ đồng nghĩa kiểu: đặt tên thông tin cho các kiểu phức tạp

6.1.2. Hàm cấp độ kiểu với sự khớp mẫu

6.1.3. Sử dụng biểu thức case trong kiểu dữ liệu

6.2. Định nghĩa hàm với số lượng tham số biến đổi

6.2.1. Một hàm cộng

6.2.2. Đầu ra định dạng: một hàm printf an toàn kiểu dữ liệu

6.3. Cải thiện kho dữ liệu tương tác với các sơ đồ

6.3.1. Tinh chỉnh loại DataStore

6.3.2. Sử dụng một bản ghi cho DataStore

6.3.3. Sửa lỗi biên dịch bằng cách sử dụng lỗ hổng

6.3.4. Hiển thị các mục trong cửa hàng

6.3.5. Phân tích các mục theo schema

6.3.6. Cập nhật lược đồ

6.3.7. Xếp thứ tự các biểu thức với Maybe sử dụng cú pháp do

6.4. Tóm tắt

Chương 7. Giao diện: sử dụng kiểu tổng quát bị ràng buộc

7.1. So sánh tổng quát với Eq và Ord

7.1.1. Kiểm tra sự bằng nhau với Eq

7.1.2. Định nghĩa ràng buộc Eq bằng cách sử dụng giao diện và triển khai

7.1.3. Định nghĩa phương thức mặc định

7.1.4. Các triển khai bị ràng buộc

7.1.5. Giao diện bị ràng buộc: định nghĩa thứ tự với Ord

Các giao diện được định nghĩa trong Prelude

7.2.1. Chuyển đổi sang Chuỗi với Show

7.2.2. Định nghĩa các kiểu số

7.2.3. Chuyển đổi giữa các loại với Cast

7.3. Các giao diện tham số hóa bởi Kiểu -> Kiểu

7.3.1. Áp dụng một hàm cho một cấu trúc với Functor

7.3.2. Giảm cấu trúc bằng cách sử dụng Foldable

7.3.3. Cú pháp do tổng quát sử dụng Monad và Applicative

7.4. Tóm tắt

Chương 8. Sự bình đẳng: diễn tả mối quan hệ giữa các dữ liệu

8.1. Đảm bảo tính tương đương của dữ liệu với các kiểu tương đương

8.1.1. Thực hiện exactLength, nỗ lực đầu tiên

8.1.2. Biểu thị sự bình đẳng của Nats dưới dạng kiểu

8.1.3. Kiểm tra tính bằng nhau của Nats

8.1.4. Chức năng như là chứng minh: thao tác trên các đẳng thức

8.1.5. Triển khai exactLength, lần thử thứ hai

8.1.6. Đẳng thức nói chung: loại =

8.2. Bình đẳng trong thực tiễn: các loại và lý do

8.2.1. Đảo ngược một véc-tơ

Kiểm tra kiểu và đánh giá

8.2.3. Cấu trúc viết lại: viết lại một kiểu bằng cách sử dụng sự bằng nhau

8.2.4. Uỷ quyền chứng minh và viết lại vào các khoảng trống

8.2.5. Ghi chú các vector, xem lại

8.3. Kiểu rỗng và tính có thể quyết định

8.3.1. Void: một loại không có giá trị nào

8.3.2. Khả quyết: kiểm tra các thuộc tính với độ chính xác

8.3.3. DecEq: một giao diện cho sự bằng nhau có thể quyết định

8.4. Tóm tắt

Chương 9. Định đề: diễn tả giả định và hợp đồng trong kiểu dữ liệu

9.1. Kiểm tra thành viên: đại lượng Elem

9.1.1. Xóa một phần tử khỏi Vect

9.1.2. Loại Elem: đảm bảo một giá trị nằm trong một véc tơ

9.1.3. Loại bỏ một phần tử khỏi Vect: các loại như là hợp đồng

9.1.4. đối số tự động ngầm: tự động xây dựng chứng minh

9.1.5. Các toán tử có thể quyết định: quyết định thành viên của một vector

9.2. Biểu thị trạng thái chương trình bằng kiểu dữ liệu: một trò chơi đoán số

9.2.1. Đại diện cho trạng thái của trò chơi

Chức năng trò chơi cấp cao 9.2.2

9.2.3. Một phép đo để xác thực đầu vào của người dùng: ValidInput

Xử lý một dự đoán

9.2.5. Quyết định tính hợp lệ của đầu vào: kiểm tra ValidInput

9.2.6. Hoàn thành việc triển khai trò chơi cấp cao nhất

9.3. Tóm tắt

Chương 10. Các góc nhìn: mở rộng kiểm tra mẫu

10.1. Định nghĩa và sử dụng các chế độ xem

10.1.1. Khớp mục cuối cùng trong danh sách

10.1.2. Xây dựng các chế độ xem: chức năng bao phủ

10.1.3. với các khối: cú pháp cho việc khớp mẫu mở rộng

10.1.4. Ví dụ: đảo ngược một danh sách bằng cách sử dụng một view

10.1.5. Ví dụ: sắp xếp hợp nhất

10.2. Các view đệ quy: sự kết thúc và hiệu suất

10.2.1. “Snoc” danh sách: duyệt một danh sách theo chiều ngược lại

10.2.2. Các view đệ quy và cấu trúc with

10.2.3. Duyệt qua nhiều đối số: lồng với các khối

10.2.4. Nhiều lượt duyệt: Data.List.Views

10.3. Trừu tượng hóa dữ liệu: ẩn cấu trúc của dữ liệu bằng cách sử dụng các chế độ xem

10.3.1. Lạc đề: các mô-đun trong Idris

10.3.2. Kho dữ liệu, xem lại

10.3.3. Duyệt nội dung của cửa hàng bằng cách nhìn nhận

10.4. Tóm tắt

3. Idris và thế giới thực

Chương 11. Dòng dữ liệu và quy trình: làm việc với dữ liệu vô hạn

11.1. Dòng chảy: tạo và xử lý danh sách vô hạn

11.1.1. Ghi nhãn các phần tử trong danh sách

11.1.2. Sản xuất một danh sách vô hạn các số

11.1.3. Lạc đề: điều gì có nghĩa là một hàm là tổng quát?

11.1.4. Xử lý danh sách vô hạn

11.1.5. Kiểu dữ liệu Stream

11.1.6. Một bài kiểm tra toán học sử dụng luồng số ngẫu nhiên

11.2. Quy trình vô hạn: viết chương trình tổng thể tương tác

11.2.1. Mô tả các quá trình vô hạn

11.2.2. Thực thi các quy trình vô hạn

11.2.3. Thực thi các quá trình vô hạn như là các hàm tổng quát

11.2.4. Tạo cấu trúc vô hạn bằng cách sử dụng kiểu Lazy

11.2.5. Mở rộng cú pháp do cho InfIO

11.2.6. Một bài kiểm tra toán học tổng hợp

11.3. Các chương trình tương tác có kết thúc

11.3.1. Tinh chỉnh InfIO: giới thiệu việc kết thúc

11.3.2. Lệnh chuyên ngành

11.3.3. Sắp xếp các lệnh bằng cú pháp do

11.4. Tóm tắt

Chương 12. Viết chương trình với trạng thái

12.1. Làm việc với trạng thái có thể thay đổi

12.1.1. Ví dụ về duyệt cây

12.1.2. Biểu diễn trạng thái có thể thay đổi bằng cách sử dụng một cặp

12.1.3. Trạng thái, một loại để mô tả các hoạt động có trạng thái

12.1.4. Duyệt cây với Trạng thái

12.2. Một triển khai tùy chỉnh của State

12.2.1. Định nghĩa State và runState

12.2.2. Định nghĩa các triển khai Functor, Applicative và Monad cho State

12.3. Một chương trình hoàn chỉnh với trạng thái: làm việc với các bản ghi

12.3.1. Các chương trình tương tác có trạng thái: ôn tập quiz số học

12.3.2. Trạng thái phức tạp: xác định các bản ghi lồng nhau

Cập nhật giá trị trường bản ghi

Cập nhật các trường ghi theo cách áp dụng chức năng

12.3.5. Thực hiện bài quiz

12.3.6. Chạy các chương trình tương tác và có trạng thái: thực thi bài kiểm tra

12.4. Tóm tắt

Chương 13. Máy trạng thái: xác minh giao thức trong kiểu dữ liệu

13.1. Máy trạng thái: theo dõi trạng thái trong loại

13.1.1. Máy trạng thái hữu hạn: mô hình hóa một cánh cửa như một kiểu dữ liệu

13.1.2. Phát triển tương tác của chuỗi hoạt động cửa

13.1.3. Trạng thái vô hạn: mô hình hóa một cái máy bán hàng tự động

Mô tả máy bán hàng đã được xác minh 13.1.4.

13.2. Các kiểu phụ thuộc trong trạng thái: thực hiện một ngăn xếp

13.2.1. Đại diện cho các thao tác ngăn xếp trong một máy trạng thái

13.2.2. Triển khai ngăn xếp sử dụng Vect

13.2.3. Sử dụng ngăn xếp một cách tương tác: một máy tính dựa trên ngăn xếp

13.3. Tóm tắt

Chương 14. Máy trạng thái phụ thuộc: xử lý phản hồi và lỗi

14.1. Xử lý lỗi trong các trạng thái chuyển tiếp

14.1.1. Tinh chỉnh mô hình cửa: đại diện cho sự cố

Một mô tả giao thức cửa đã được xác minh và kiểm tra lỗi.

14.2. Tính chất bảo mật trong kiểu dữ liệu: mô hình hóa một máy ATM

14.2.1. Định nghĩa các trạng thái cho máy rút tiền tự động (ATM)

14.2.2. Định nghĩa một loại cho cây ATM

14.2.3. Mô phỏng một máy ATM tại bảng điều khiển: thực thi ATMCmd

14.2.4. Cải tiến các điều kiện tiên quyết bằng cách sử dụng tự động ngụ ý

14.3. Một trò chơi đoán đúng đã được xác minh: mô tả quy tắc bằng kiểu loại

14.3.1. Định nghĩa một trạng thái trò chơi trừu tượng và các thao tác

14.3.2. Định nghĩa một kiểu cho trạng thái trò chơi

14.3.3. Triển khai trò chơi

14.3.4. Định nghĩa trạng thái trò chơi cụ thể

14.3.5. Chạy trò chơi: thực thi GameLoop

14.4. Tóm tắt

Chương 15. Lập trình đồng thời an toàn kiểu dữ liệu

15.1. Nguyên thủy cho lập trình đồng thời trong Idris

15.1.1. Định nghĩa các quá trình đồng thời

Thư viện Channels: Truyền tin nguyên thủy

15.1.3. Vấn đề với các kênh: lỗi kiểu và tình trạng chặn

15.2. Định nghĩa một kiểu cho việc truyền tin an toàn

15.2.1. Mô tả các quá trình chuyển tiếp tin nhắn trong một kiểu

15.2.2. Tổng hợp các quy trình bằng cách sử dụng Inf

`15.2.3. Đảm bảo phản hồi bằng cách sử dụng máy trạng thái và Inf`

15.2.4. Các quy trình truyền tin tổng quát

15.2.5. Định nghĩa một mô-đun cho Quy trình

15.2.6. Ví dụ 1: Xử lý danh sách

15.2.7. Ví dụ 2: Một quy trình đếm từ

15.3. Tóm tắt

Phụ lục A. Cài đặt Idris và chế độ chỉnh sửa

Biên dịch viên và môi trường Idris

Hệ điều hành Mac

Cửa sổ

"Nền tảng giống Unix, cài đặt từ mã nguồn"

Chế độ biên tập

Nguyên tử

Các biên tập viên khác

Phụ lục B. Các lệnh chỉnh sửa tương tác

Phụ lục C. Lệnh REPL

Phụ lục D. Tài liệu tham khảo thêm

Lập trình hàm trong Haskell

Các ngôn ngữ và công cụ khác có hệ thống kiểu mạnh mẽ

Cơ sở lý thuyết

Lập trình hàm tổng quát

Các loại cho độ đồng thời

Phụ lục

Phụ lục

Mục lục

Danh sách hình ảnh

Danh sách bảng

Danh sách các mục hồ sơ

Preface

Máy tính có mặt ở khắp mọi nơi, và chúng ta phụ thuộc vào phần mềm hàng ngày. Ngoài việc điều khiển máy tính để bàn và máy tính xách tay, phần mềm còn kiểm soát các hoạt động liên lạc, ngân hàng, hạ tầng giao thông, và ngay cả các thiết bị gia dụng của chúng ta. Dù vậy, việc phần mềm không đáng tin cậy được coi là một điều hiển nhiên. Nếu một chiếc laptop hoặc điện thoại di động bị hỏng, chỉ đơn giản là bất tiện và yêu cầu khởi động lại (có thể kèm theo những lời mắng mỏ vì mất vài phút làm việc cuối cùng). Mặt khác, nếu phần mềm điều khiển một ứng dụng hoặc máy chủ thiết yếu cho doanh nghiệp bị hỏng, có thể mất rất nhiều thời gian và tiền bạc. Đối với các hệ thống quan trọng về an toàn, hậu quả có thể còn tồi tệ hơn.

Trong nhiều năm qua, do đó, các nhà nghiên cứu khoa học máy tính đã tìm kiếm các phương pháp để cải thiện độ bền vững và an toàn của phần mềm. Một trong những cách tiếp cận trong số nhiều cách là sử dụng kiểu dữ liệu để mô tả những gì một chương trình dự kiến sẽ thực hiện. Cụ thể, bằng cách sử dụng các kiểu dữ liệu phụ thuộc, bạn mô tả các thuộc tính chính xác của một chương trình. Ý tưởng là nếu bạn có thể diễn đạt ý định của một chương trình trong kiểu của nó, và chương trình đó kiểm tra kiểu thành công, thì chương trình đó phải hoạt động như mong muốn. Một mục tiêu quan trọng (nếu khá tham vọng và dài hạn) của ngôn ngữ lập trình Idris là làm cho kết quả của nghiên cứu này trở nên dễ tiếp cận đối với các nhà phát triển phần mềm nói chung, và do đó giảm khả năng xảy ra các lỗi phần mềm nghiêm trọng.

Ban đầu, trọng tâm của cuốn sách này là lập trình trong Idris: chỉ ra cách sử dụng hệ thống loại của nó để đảm bảo những thuộc tính quan trọng của các chương trình. Dưới sự hướng dẫn của biên tập viên phát triển Dan Maharry, và nhờ vào những nỗ lực của biên tập viên phát triển kỹ thuật Andrew Gibson, cuốn sách đã phát triển để trở thành một phần không kém về quy trình lập trình với các loại phụ thuộc như về cách các chương trình thu được hoạt động. Bạn sẽ học về những nguyên tắc cơ bản của các loại phụ thuộc, cách sử dụng loại để định nghĩa các chương trình một cách tương tác, và cách tinh chỉnh các chương trình và loại khi hiểu biết của bạn về một vấn đề phát triển. Bạn cũng sẽ tìm hiểu về một số ứng dụng thực tế của phát triển theo loại, đặc biệt là trong việc xử lý trạng thái, giao thức và tính đồng thời.

Idris ra đời từ việc nghiên cứu của tôi về xác minh chương trình và thiết kế ngôn ngữ với các loại phụ thuộc. Sau khi dành nhiều năm đắm chìm trong khái niệm lập trình với các loại phụ thuộc, tôi cảm thấy có một nhu cầu về một ngôn ngữ được thiết kế cho cả các nhà phát triển lẫn các nhà nghiên cứu. Tôi hy vọng bạn sẽ vui vẻ như tôi đã có khi phát triển nó trong việc tìm hiểu về phát triển dựa trên kiểu với Idris!

Acknowledgments

Nhiều người đã giúp đỡ trong việc viết cuốn sách này, và nó sẽ không tồn tại nếu không có họ. Đặc biệt, tôi cảm ơn Dan Maharry, người đã khuyến khích tôi làm rõ hơn các ý tưởng về phát triển dựa trên kiểu. Câu thần châm “kiểu, định nghĩa, tinh chỉnh,” mà xuất hiện xuyên suốt cuốn sách, là gợi ý của Dan. Tôi cũng xin cảm ơn Andrew Gibson, người đã làm việc một cách tỉ mỉ với tất cả các ví dụ và bài tập trong cuốn sách, đảm bảo rằng chúng hoạt động, kiểm tra rằng các bài tập là có thể giải được, và gợi ý nhiều cải tiến cho phần văn bản và các giải thích. Tổng thể, tôi muốn cảm ơn đội ngũ tại Manning Publications vì đã giúp biến cuốn sách này thành hiện thực.

Thiết kế của Idris chịu ảnh hưởng lớn từ vài thập kỷ nghiên cứu về lý thuyết kiểu, lập trình hàm và thiết kế ngôn ngữ. Tôi cảm ơn James McKinna và Conor McBride đặc biệt vì đã dạy tôi những nguyên tắc cơ bản của lý thuyết kiểu khi tôi là sinh viên cao học tại Đại học Durham, và vì sự tư vấn và khuyến khích liên tục của họ từ đó đến nay. Tôi cũng muốn cảm ơn các nhà nghiên cứu và phát triển có trách nhiệm với các ngôn ngữ và hệ thống đã truyền cảm hứng cho công việc của tôi, cụ thể là các công cụ như Haskell, Epigram, Agda và Coq. Idris không thể tồn tại nếu không có những công việc đã diễn ra trước đó, và tôi chỉ có thể hy vọng rằng nó, theo cách của nó, sẽ truyền cảm hứng cho những người khác trong tương lai. Xem phụ lục D để tham khảo một số công việc đã truyền cảm hứng cho Idris.

Nhiều đồng nghiệp và sinh viên tại Đại học St. Andrews và một số nơi khác đã cung cấp phản hồi hữu ích về các bản thảo trước đó của các chương và đã kiên nhẫn trong khi tôi làm việc với cuốn sách thay vì chú tâm vào những việc khác. Đặc biệt, tôi xin cảm ơn Ozgur Akgun, Nicola Botta, Sam Elliot, Simon Fowler, Nicolas Gagliani (người đã đóng góp mở rộng cho trình soạn thảo Atom mà bạn sẽ sử dụng trong suốt cuốn sách), Jan de Muijnck-Hughes, Markus Pfeiffer, Chris Schwaab và Matúš Tejiščák vì những nhận xét và gợi ý của họ. Tôi chân thành xin lỗi bất kỳ ai khác mà tôi đã quên không nêu tên!

Những độc giả đã mua quyền truy cập sớm và những người đánh giá các bản thảo trước đó đã đóng góp nhiều bình luận và gợi ý hữu ích. Những người đánh giá này bao gồm Alexander A. Myltsev, Álvaro Falquina, Arnaud Bailly, Carsten Jørgensen, Christine Koppelt, Giovanni Ruggiero, Ian Dees, Juan Gabriel Bono, Mattias Lundell, Phil de Joux, Rintcius Blok, Satadru Roy, Sergey Selyugin, Todd Fine và Vitaly Bragilevsky.

Tôi không thể tự triển khai Idris. Kể từ khi tôi bắt đầu phát triển phiên bản hiện tại vào cuối năm 2011, đã có nhiều cộng tác viên, nhưng hơn hết, tôi muốn cảm ơn David Christiansen, người chịu trách nhiệm cho nhiều sự tinh chỉnh trong Idris REPL và các công cụ chỉnh sửa tương tác; anh ấy cũng đã làm việc chăm chỉ để giúp đỡ những người mới tham gia dự án. Cũng cần gửi lời cảm ơn đến các cộng tác viên khác: Ozgur Akgun, Ahmad Salim Al-Sibahi, Edward Chadwick Amsden, Michael R. Bernstein, Jan Bessai, Nicola Botta, Vitaly Bragilevsky, Jakob Brünker, Alyssa Carter, Carter Charbonneau, Aaron Craelius, Jason Dagit, Adam Sandberg Eriksson, Guglielmo Fachini, Simon Fowler, Zack Grannan, Sean Hunt, Cezar Ionescu, Heath Johns, Irene Knapp, Paul Koerbitz, Niklas Larsson, Shea Levy, Mathnerd314, Hannes Mehnert, Mekeor Melire, Melissa Mozifian, Jan de Muijnck-Hughes, Dominic Mulligan, Echo Nolan, Tom Prince, raichoo, Philip Rasmussen, Aistis Raulinaitis, Reynir Reynisson, Seo Sanghyeon, Benjamin Saunders, Alexander Shabalin, Jeremy W. Sherman, Timo Petteri Sinnemäki, JP Smith, startling, Chetan T, Matúš Tejiščák, Dirk Ullrich, Leif Warner, Daniel Waterworth, Eric Weinstein, Jonas Westerlund, Björn Aili, và Zheng Jihui.

Cuối cùng, tôi xin cảm ơn cha mẹ tôi, việc mua một chiếc BBC Micro vào năm 1983 đã dẫn dắt tôi trên con đường này; và cảm ơn Emma, vì đã chờ đợi một cách kiên nhẫn để tôi hoàn thành điều này, và vì đã mang cho tôi cà phê để giúp tôi tiếp tục.

About this Book

Phát triển dựa trên kiểu với Idris là về việc làm cho các kiểu hoạt động hiệu quả cho bạn. Các kiểu thường được coi là công cụ để kiểm tra lỗi, với lập trình viên viết một chương trình hoàn chỉnh trước và sử dụng trình kiểm tra kiểu để phát hiện lỗi. Trong phát triển dựa trên kiểu, bạn sử dụng các kiểu như một công cụ để xây dựng chương trình, và trình kiểm tra kiểu như một trợ lý của bạn để hướng dẫn bạn đến một chương trình hoàn chỉnh và hoạt động.

Cuốn sách này bắt đầu bằng cách mô tả những gì bạn có thể diễn đạt với các kiểu; sau đó, nó giới thiệu các đặc điểm cốt lõi của ngôn ngữ lập trình Idris. Cuối cùng, nó mô tả một số ứng dụng thực tiễn hơn của phát triển dựa trên kiểu.

Who should read this book

Cuốn sách này nhằm vào các lập trình viên muốn tìm hiểu về những tiến bộ mới nhất trong việc sử dụng các hệ thống kiểu tinh vi để phát triển phần mềm đáng tin cậy. Nó hướng đến mục tiêu cung cấp một giới thiệu dễ tiếp cận về các kiểu phụ thuộc, và cho thấy cách các kỹ thuật dựa trên kiểu hiện đại có thể được áp dụng vào các vấn đề trong thế giới thực.

Người đọc lý tưởng sẽ đã quen thuộc với các khái niệm lập trình hàm như closure và hàm bậc cao, mặc dù cuốn sách sẽ giới thiệu những khái niệm này và các khái niệm khác khi cần thiết. Kiến thức về một ngôn ngữ lập trình hàm khác như Haskell, OCaml hoặc Scala sẽ đặc biệt hữu ích, mặc dù không có ngôn ngữ nào được giả định.

Roadmap

Cuốn sách này được chia thành ba phần. Phần 1 (các chương 1 và 2) giới thiệu các khái niệm và cung cấp cái nhìn tổng quan về ngôn ngữ lập trình Idris:

Chapter 1 introduces type-driven development and gets you started with the Idris environment.
Chapter 2 covers the basics of Idris programming, including primitive types and structuring Idris programs.

Phần 2 (các chương 3–10) giới thiệu các đặc điểm ngôn ngữ cốt lõi của Idris:

Chapter 3 discusses interactive development using the Atom editor and describes how using more-precise types means that the type checker can help you write programs.
Chapter 4 explains how to define your own data types and presents a first example of writing a larger interactive program in the type-driven style.
Chapter 5 describes interactive programs in more depth, including how to use types to help validate user inputs to interactive programs.
Chapter 6 introduces type-level programming, showing how to write functions that calculate types and how to use them in practice.
Chapter 7 describes how to use interfaces to write programs with generic types.
Chapter 8 explains how you can use types to express relationships between data, particularly to describe properties of data and to guarantee that functions behave a certain way.
Chapter 9 explains further how types can express contracts that functions must satisfy, including an example that shows how to use types to describe the state of a system.
Chapter 10 introduces views, which are alternative ways of inspecting and traversing data structures.

Phần 3 (các chương 11–15) mô tả một số ứng dụng của Idris trong phát triển phần mềm thực tế, đặc biệt là làm việc với trạng thái và các chương trình tương tác.

Chapter 11 describes how to work with potentially infinite data, such as streams, and how to write and reason about interactive programs that could run indefinitely.
Chapter 12 explains how to write programs with state and how to represent and manipulate complex state using records.
Chapter 13 shows how to express a state machine in an Idris type, and how to use the type to guarantee that programs follow protocols correctly.
Chapter 14 describes more-sophisticated state machines, how to handle errors and feedback from an environment, and how to represent security properties of a system in its type.
Chapter 15 concludes the book with a worked example: type-driven development of a small library for concurrent programming.

Nói chung, mỗi chương xây dựng dựa trên các khái niệm được giới thiệu trong các chương trước, vì vậy bạn nên đọc các chương theo thứ tự. Quan trọng nhất, cuốn sách mô tả quy trình phát triển dựa trên kiểu dữ liệu và xây dựng chương trình tương tác từ một kiểu. Do đó, tôi khuyến nghị mạnh mẽ rằng bạn nên làm theo các ví dụ trên máy tính khi bạn đọc. Hơn nữa, nếu bạn đang đọc eBook, hãy gõ các ví dụ - đừng chỉ sao chép và dán.

Có các bài tập trong suốt mỗi chương, vì vậy, khi bạn đọc, hãy chắc chắn rằng bạn hoàn thành các bài tập để củng cố sự hiểu biết của mình. Các giải pháp mẫu có sẵn trực tuyến từ trang web của cuốn sách tại www.manning.com/books/type-driven-development-with-idris.

Có bốn phụ lục: Phụ lục A mô tả cách cài đặt Idris và chế độ chỉnh sửa Atom, mà chúng ta sẽ sử dụng xuyên suốt cuốn sách. Phụ lục B tóm tắt các lệnh chỉnh sửa tương tác được hỗ trợ bởi Atom. Phụ lục C tóm tắt các lệnh bạn có thể sử dụng trong môi trường Idris. Cuối cùng, phụ lục D cung cấp tài liệu tham khảo về một số công trình đã truyền cảm hứng cho Idris, và nơi bạn có thể tìm hiểu thêm về nền tảng lý thuyết và các công cụ liên quan.

Code conventions and downloads

Cuốn sách này chứa nhiều ví dụ về mã nguồn, cả dưới dạng danh sách có số thứ tự và nội dung trong văn bản thông thường. Ở cả hai trường hợp, mã nguồn được định dạng bằng phông chữ cố định như thế này để tách biệt nó với văn bản thông thường.

Trong nhiều trường hợp, mã nguồn gốc đã được định dạng lại; tôi đã thêm xuống dòng và điều chỉnh lề để phù hợp với không gian trang có sẵn trong cuốn sách. Ngoài ra, các bình luận trong mã nguồn thường đã bị xóa khỏi danh sách khi mã được mô tả trong văn bản. Các chú thích mã đi kèm với nhiều danh sách, làm nổi bật các khái niệm quan trọng.

Tất cả mã nguồn trong cuốn sách này có sẵn trực tuyến từ trang web của cuốn sách (www.manning.com/books/type-driven-development-with-idris) và đã được thử nghiệm với Idris 1.0. Mã nguồn cũng có trên một kho Git tại đây: https://github.com/edwinb/TypeDD-Samples.

Author Online

Việc mua sách "Phát triển dựa trên kiểu với Idris" bao gồm quyền truy cập miễn phí vào một diễn đàn web riêng do Manning Publications điều hành, nơi bạn có thể đưa ra nhận xét về cuốn sách, đặt câu hỏi kỹ thuật và nhận trợ giúp từ tác giả cũng như từ những người dùng khác. Để truy cập và đăng ký vào diễn đàn, hãy mở trình duyệt web của bạn và truy cập www.manning.com/books/type-driven-development-with-idris. Trang này cung cấp thông tin về cách tham gia diễn đàn sau khi bạn đã đăng ký, loại trợ giúp nào có sẵn và các quy tắc ứng xử trên diễn đàn.

Cam kết của Manning đối với độc giả của chúng tôi là tạo ra một không gian nơi mà cuộc đối thoại ý nghĩa có thể diễn ra giữa các độc giả cá nhân và giữa độc giả với tác giả. Đây không phải là một cam kết đối với một mức độ tham gia cụ thể nào từ phía tác giả, người có đóng góp vào diễn đàn là tự nguyện (và không được trả tiền). Chúng tôi gợi ý bạn nên đặt ra những câu hỏi thách thức để giữ cho sự quan tâm của anh ấy không bị lạc hướng!

Diễn đàn Author Online và lưu trữ các cuộc thảo luận trước đây sẽ được truy cập từ trang web của nhà xuất bản miễn là cuốn sách còn in.

Other online resources

Nếu bạn muốn tìm hiểu thêm về Idris, bạn có thể tìm thêm tài nguyên trên trang web của Idris: http://idris-lang.org/. Bạn cũng có thể tìm sự trợ giúp ở một số nơi khác:

The idris-lang Google Group is an active group discussing all aspects of Idris. The group welcomes questions from beginners and more-advanced users alike.
There is an IRC channel, #idris on irc.freenode.net, which is similarly open to questions.
You can ask and answer questions using the Idris tag on Stack Overflow.

About the Author

EDWIN BRADY dẫn dắt việc thiết kế và triển khai ngôn ngữ lập trình Idris. Ông là giảng viên Khoa học Máy tính tại Đại học St. Andrews ở Scotland, và thường xuyên phát biểu tại các hội nghị. Khi không làm những việc đó, bạn có thể tìm thấy ông đang chơi một ván cờ Go, xem một trận cricket, hoặc ở đâu đó trên một ngọn đồi ở giữa Scotland.

About the Cover Illustration

Hình ảnh trên bìa cuốn Tư Duy Dựa Trên Kiểu với Idris được chú thích là "La Gasconne," hay "Một người phụ nữ từ Gascony." Minh họa này được lấy từ một bộ sưu tập các tác phẩm của nhiều nghệ sĩ, do Louis Curmer biên soạn và xuất bản tại Paris vào năm 1841. Tiêu đề của bộ sưu tập là Les Français peints par eux-mêmes, có thể dịch là Người Pháp được vẽ bởi chính họ. Mỗi minh họa đều được vẽ tinh xảo và tô màu bằng tay, và sự đa dạng phong phú của các bức tranh trong bộ sưu tập khiến chúng ta nhớ rõ ràng rằng các vùng, thị trấn, làng mạc và khu phố trên thế giới đã cách biệt văn hóa như thế nào chỉ cách đây 200 năm. Tách biệt khỏi nhau, mọi người đã nói những tiếng địa phương và ngôn ngữ khác nhau. Trên đường phố hoặc ở nông thôn, thật dễ dàng để nhận biết nơi họ sống và nghề nghiệp hoặc vị trí xã hội của họ chỉ bằng cách nhìn vào trang phục của họ.

Các quy tắc ăn mặc đã thay đổi kể từ đó, và sự đa dạng theo vùng, vốn phong phú vào thời điểm đó, đã phai nhạt. Hiện giờ thật khó để phân biệt cư dân của các châu lục khác nhau, chứ đừng nói đến các thành phố hoặc vùng khác nhau. Có lẽ chúng ta đã trao đổi sự đa dạng văn hóa để có một cuộc sống cá nhân phong phú hơn—chắc chắn là để có một cuộc sống công nghệ phong phú và nhanh chóng hơn.

Vào thời điểm mà thật khó để phân biệt một cuốn sách máy tính với cuốn sách khác, Manning kỷ niệm sự sáng tạo và sáng kiến của ngành công nghiệp máy tính với các bìa sách dựa trên sự đa dạng phong phú của đời sống khu vực cách đây hai thế kỷ, được hồi sinh bởi những hình ảnh từ các bộ sưu tập như bộ sưu tập này.

Part 1.
Introduction

Trong phần đầu này, bạn sẽ bắt đầu với Idris và tìm hiểu về những ý tưởng phía sau phát triển dựa trên kiểu dữ liệu. Tôi sẽ đưa bạn đi tham quan nhanh về môi trường Idris, và bạn sẽ viết một số chương trình đơn giản nhưng hoàn chỉnh.

Trong chương đầu tiên, tôi sẽ giải thích thêm về ý nghĩa của phát triển dựa trên kiểu (type-driven development). Quan trọng nhất, tôi sẽ định nghĩa điều tôi muốn nói đến khi nhắc đến “kiểu” và đưa ra một số ví dụ về cách bạn có thể sử dụng các kiểu biểu đạt để mô tả mục đích của các chương trình của bạn một cách chính xác hơn. Tôi cũng sẽ giới thiệu hai đặc điểm nổi bật nhất của ngôn ngữ Idris: các lỗ hổng, đại diện cho các phần của chương trình chưa được viết, và việc sử dụng kiểu như một cấu trúc ngôn ngữ bậc nhất.

Trước khi bạn đi quá sâu vào phát triển dựa trên kiểu trong Idris, điều quan trọng là phải nắm vững các kiến thức cơ bản về ngôn ngữ này. Do đó, trong chương 2, tôi sẽ thảo luận về một số cấu trúc ngôn ngữ cơ bản, nhiều trong số đó sẽ quen thuộc với bạn từ các ngôn ngữ khác, và chỉ ra cách xây dựng các chương trình hoàn chỉnh trong Idris.

Chapter 1.
Overview

Chương này đề cập đến

Introducing type-driven development
The essence of pure functional programming
First steps with Idris

Cuốn sách này dạy một phương pháp mới để xây dựng phần mềm mạnh mẽ, phát triển dựa trên loại, sử dụng ngôn ngữ lập trình Idris. Thông thường, các loại được coi là công cụ để kiểm tra lỗi, với lập trình viên viết một chương trình hoàn chỉnh trước và sử dụng trình biên dịch hoặc hệ thống thời gian chạy để phát hiện lỗi loại. Trong phát triển dựa trên loại, chúng tôi sử dụng các loại như là công cụ để xây dựng chương trình. Chúng tôi đặt loại lên hàng đầu, coi nó như một kế hoạch cho một chương trình, và sử dụng trình biên dịch và kiểm tra loại như là trợ lý của chúng tôi, hướng dẫn chúng tôi đến một chương trình hoàn chỉnh và hoạt động thỏa mãn loại. Càng nhiều đặc tả và chính xác chúng tôi đưa ra trước, chúng tôi càng có thể tự tin hơn rằng chương trình kết quả sẽ đúng.

Types and tests

Tên gọi “phát triển theo kiểu” gợi ý một phép ẩn dụ với phát triển theo kiểm thử. Có một sự tương đồng, ở chỗ việc viết các bài kiểm thử trước giúp xác định mục đích của chương trình và liệu nó có đáp ứng một số yêu cầu cơ bản hay không. Sự khác biệt là, khác với các bài kiểm thử, thường chỉ dùng để chỉ ra sự hiện diện của lỗi, kiểu (nếu được sử dụng một cách hợp lý) có thể chỉ ra sự vắng mặt của lỗi. Nhưng mặc dù kiểu giảm bớt nhu cầu về kiểm thử, chúng hiếm khi loại bỏ hoàn toàn nó.

Idris là một ngôn ngữ lập trình tương đối mới, được thiết kế từ đầu để hỗ trợ phát triển dựa trên kiểu. Một phiên bản thử nghiệm đầu tiên xuất hiện vào năm 2008, với việc phát triển phiên bản hiện tại bắt đầu vào năm 2011. Nó được xây dựng dựa trên hàng thập kỷ nghiên cứu về các nền tảng lý thuyết và thực tiễn của các ngôn ngữ lập trình và hệ thống kiểu.

Trong Idris, loại là một cấu trúc ngôn ngữ hạng nhất. Các loại có thể được thao tác, sử dụng, truyền làm đối số cho các hàm, và trả về từ các hàm giống như bất kỳ giá trị nào khác, chẳng hạn như số, chuỗi, hoặc danh sách. Đây là một ý tưởng đơn giản nhưng mạnh mẽ:

It allows relationships to be expressed between values; for example, that two lists have the same length.
It allows assumptions to be made explicit and checkable by the compiler. For example, if you assume that a list is non-empty, Idris can ensure this assumption always holds before the program is run.
If desired, it allows program behavior to be formally stated and proven correct.

Trong chương này, tôi sẽ giới thiệu ngôn ngữ lập trình Idris và cung cấp một cái nhìn tổng quan về các tính năng và môi trường của nó. Tôi cũng sẽ đưa ra một cái nhìn tổng quan về phát triển dựa trên kiểu dữ liệu, thảo luận về lý do tại sao kiểu dữ liệu lại quan trọng trong các ngôn ngữ lập trình và cách chúng có thể được sử dụng để hướng dẫn phát triển phần mềm. Nhưng trước tiên, điều quan trọng là phải hiểu chính xác cái mà chúng ta đề cập khi nói về “kiểu dữ liệu.”

1.1. What is a type?

Chúng ta được dạy từ khi còn nhỏ để nhận diện và phân biệt các loại đối tượng. Khi còn là một đứa trẻ, có thể bạn đã có một món đồ chơi phân loại hình dạng. Nó bao gồm một cái hộp với các lỗ hình dạng khác nhau ở trên (xem hình 1.1) và một số hình dạng có thể vừa qua các lỗ đó. Đôi khi chúng đi kèm với một cái búa nhỏ bằng nhựa. Ý tưởng là để vừa mỗi hình dạng (hãy coi đây là một "giá trị") vào lỗ phù hợp (hãy coi đây là một " loại"), có thể có sự tác động từ cái búa.

Figure 1.1.
The top of a shape-sorter toy. The shapes correspond to the types of objects that will fit through the holes.

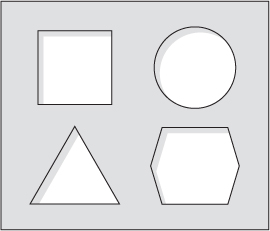
Trong lập trình, kiểu dữ liệu là một cách để phân loại giá trị. Chẳng hạn, các giá trị 94, "vật", và [1,2,3,4,5] có thể lần lượt được phân loại là một số nguyên, một chuỗi, và một danh sách các số nguyên. Cũng giống như bạn không thể đặt một hình vuông vào lỗ tròn trong bộ phân loại hình dạng, bạn không thể sử dụng một chuỗi như "vật" trong một phần của chương trình nơi bạn cần một số nguyên.

Tất cả các ngôn ngữ lập trình hiện đại phân loại các giá trị theo kiểu, mặc dù chúng khác nhau rất nhiều về thời điểm và cách thức thực hiện điều đó (ví dụ, liệu chúng có được kiểm tra tĩnh tại thời điểm biên dịch hay động tại thời điểm chạy, liệu các chuyển đổi giữa các kiểu có tự động hay không, và nhiều thứ khác).

Các loại đóng vai trò quan trọng trong nhiều lĩnh vực:

For a machine, types describe how bit patterns in memory are to be interpreted.
For a compiler or interpreter, types help ensure that bit patterns are interpreted consistently when a program runs.
For a programmer, types help name and organize concepts, aiding documentation and supporting interactive editing environments.

Từ quan điểm của chúng tôi trong cuốn sách này, mục đích quan trọng nhất của kiểu dữ liệu là cái thứ ba. Kiểu giúp lập trình viên theo nhiều cách:

By allowing for the naming and organization of concepts (such as Square, Circle, Triangle, and Hexagon)
By providing explicit documentation of the purposes of variables, functions, and programs
By driving code completion in an interactive editing environment

Như bạn sẽ thấy, phát triển dựa trên kiểu (type-driven development) tận dụng rất nhiều tính năng hoàn thành mã (code completion) đặc biệt. Mặc dù tất cả các ngôn ngữ lập trình tĩnh hiện đại đều hỗ trợ hoàn thành mã ở một mức độ nào đó, tính biểu đạt của hệ thống kiểu Idris dẫn đến việc tạo mã tự động mạnh mẽ.

1.2. Introducing type-driven development

Phát triển dựa trên kiểu là một phong cách lập trình trong đó chúng ta viết kiểu trước và sử dụng các kiểu đó để hướng dẫn việc định nghĩa các hàm. Quy trình tổng thể là viết các kiểu dữ liệu cần thiết, và sau đó, cho mỗi hàm, thực hiện các bước sau:

Write the input and output types.
Define the function, using the structure of the input types to guide the implementation.
Refine and edit the type and function definition as necessary.

Types as models

Khi bạn viết một chương trình, bạn thường sẽ có một mô hình khái niệm trong đầu (hoặc, nếu bạn có kỷ luật, thậm chí trên giấy) về cách nó dự kiến hoạt động, cách các thành phần tương tác và cách dữ liệu được tổ chức. Mô hình này có thể sẽ khá mơ hồ ban đầu và sẽ trở nên chính xác hơn khi chương trình phát triển và hiểu biết của bạn về khái niệm đó phát triển.

Các kiểu cho phép bạn làm cho các mô hình này trở nên rõ ràng trong mã và đảm bảo rằng việc triển khai của bạn khớp với mô hình mà bạn có trong đầu. Idris có một hệ thống kiểu biểu đạt cho phép bạn mô tả một mô hình một cách chính xác như bạn cần, và để tinh chỉnh mô hình đồng thời với việc phát triển việc triển khai.

Trong phát triển dựa trên kiểu, thay vì nghĩ về các kiểu theo cách kiểm tra, với trình kiểm tra kiểu chỉ trích bạn khi bạn mắc lỗi, bạn có thể nghĩ về các kiểu như một kế hoạch, với trình kiểm tra kiểu đóng vai trò là hướng dẫn của bạn, dẫn bạn đến một chương trình hoạt động, vững chắc. Bắt đầu với một kiểu và một thân hàm rỗng, bạn từ từ thêm chi tiết vào định nghĩa cho đến khi nó hoàn chỉnh, thường xuyên sử dụng trình biên dịch để kiểm tra rằng chương trình cho đến nay phù hợp với kiểu. Idris, như bạn sẽ sớm thấy, rất khuyến khích phong cách lập trình này bằng cách cho phép kiểm tra các định nghĩa hàm chưa hoàn chỉnh và cung cấp một ngôn ngữ diễn tả phong phú cho việc mô tả các kiểu.

Để minh họa thêm, trong phần này tôi sẽ trình bày một số ví dụ về cách bạn có thể sử dụng kiểu dữ liệu để mô tả chi tiết những gì một chương trình dự định thực hiện: phép toán ma trận, mô hình hóa một máy rút tiền tự động (ATM), và viết các chương trình đồng thời. Sau đó, tôi sẽ tóm tắt quy trình phát triển dựa trên kiểu dữ liệu và giới thiệu khái niệm về kiểu phụ thuộc, điều này sẽ cho phép bạn diễn đạt các thuộc tính chi tiết của các chương trình của bạn.

1.2.1.
Matrix arithmetic

Một ma trận là một lưới hình chữ nhật của các số, được sắp xếp thành hàng và cột. Chúng có nhiều ứng dụng khoa học, và trong lập trình, chúng có ứng dụng trong mật mã, đồ họa 3D, học máy và phân tích dữ liệu. Ví dụ, dưới đây là một ma trận 3 × 4:

Bạn có thể thực hiện các phép toán số học khác nhau trên ma trận, chẳng hạn như cộng và nhân. Để cộng hai ma trận, bạn cộng các phần tử tương ứng, như bạn thấy ở đây:

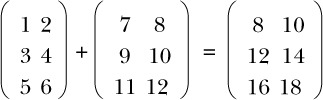
Khi lập trình với ma trận, nếu bạn bắt đầu bằng cách định nghĩa một kiểu dữ liệu Ma trận, thì phép cộng yêu cầu hai đầu vào có kiểu Ma trận và trả về một đầu ra có kiểu Ma trận. Nhưng vì việc cộng ma trận liên quan đến việc cộng các phần tử tương ứng của các đầu vào, điều gì sẽ xảy ra nếu hai đầu vào có kích thước khác nhau, như ở đây?

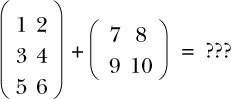
Có khả năng rằng nếu bạn đang cố gắng cộng các ma trận có kích thước khác nhau, thì bạn đã mắc phải một sai lầm ở đâu đó. Vì vậy, thay vì sử dụng loại Ma trận, bạn có thể tinh chỉnh loại này để bao gồm kích thước của ma trận và yêu cầu rằng hai ma trận đầu vào phải có cùng kích thước:

The first example of a 3 × 4 matrix now has type Matrix 3 4.
The first (correct) example of addition takes two inputs of type Matrix 3 2 and gives an output of type Matrix 3 2.

Bằng cách bao gồm các kích thước trong kiểu của một ma trận, bạn có thể mô tả các kiểu đầu vào và đầu ra của phép cộng theo cách mà việc cố gắng cộng các ma trận có kích thước khác nhau sẽ gây ra lỗi kiểu. Nếu bạn cố gắng cộng một Ma trận 3 2 và một Ma trận 2 2, chương trình của bạn sẽ không biên dịch được, huống chi là chạy.

Nếu bạn bao gồm kích thước của một ma trận trong kiểu dữ liệu của nó, thì bạn cần suy nghĩ về mối quan hệ giữa các kích thước của đầu vào và đầu ra cho mọi phép toán ma trận. Ví dụ, chuyển vị của một ma trận liên quan đến việc hoán đổi hàng thành cột và ngược lại, vì vậy nếu bạn chuyển vị một ma trận 3 × 2, bạn sẽ nhận được một ma trận 2 × 3.

Loại đầu vào của phép chuyển vị này là Ma trận 3 2, và loại đầu ra là Ma trận 2 3.

Nói chung, thay vì cung cấp kích thước chính xác trong loại, chúng tôi sẽ sử dụng biến để mô tả mối quan hệ giữa các kích thước của đầu vào và các kích thước của đầu ra. Bảng 1.1 cho thấy mối quan hệ giữa các kích thước của đầu vào và đầu ra cho ba phép toán ma trận: cộng, nhân, và chuyển vị.

Table 1.1.
Input and output types for matrix operations. The names `x`, `y`, and `z` describe, in general, how the dimensions of the inputs and outputs are related.

Hoạt động	Loại đầu vào	Loại đầu ra
Add	Matrix x y, Matrix x y	Matrix x y
Multiply	Matrix x y, Matrix y z	Matrix x z
Transpose	Matrix x y	Matrix y x

Chúng ta sẽ xem xét ma trận một cách sâu sắc trong chương 3, nơi chúng ta sẽ thực hiện một triển khai của phép chuyển vị ma trận một cách chi tiết.

1.2.2.
An automated teller machine

Ngoài việc sử dụng các kiểu để mô tả mối quan hệ giữa các đầu vào và đầu ra của các hàm, giống như trong các phép toán ma trận, bạn có thể mô tả chính xác khi nào các phép toán là hợp lệ. Ví dụ, nếu bạn đang triển khai phần mềm để điều khiển một máy ATM, bạn sẽ muốn đảm bảo rằng máy sẽ chỉ phát tiền sau khi người dùng đã đưa thẻ và xác thực mã số cá nhân (PIN) của họ.

Để hiểu cách hoạt động này, chúng ta cần xem xét các trạng thái possible mà một máy ATM có thể có:

Ready—The ATM is ready and waiting for a user to insert a card.
CardInserted—The ATM is waiting for a user, having inserted a card, to enter their PIN.
Session—A validated session is in progress, with the ATM, having validated the user’s PIN, ready to dispense cash.

Một máy ATM hỗ trợ một vài thao tác cơ bản, mỗi thao tác chỉ hợp lệ khi máy ở trong một trạng thái cụ thể, và mỗi thao tác có thể thay đổi trạng thái của máy, như được minh họa trong hình 1.2. Đây là những thao tác cơ bản:

InsertCard—Waits for the user to insert a card
EjectCard—Ejects a card from the machine
GetPIN—Prompts the user to enter a PIN
CheckPIN—Checks whether an entered PIN is correct
Dispense—Dispenses cash

Figure 1.2.
The states and valid operations on an ATM. Each operation is valid only in specific states and can change the state of the machine. `CheckPIN` changes the state only if the entered PIN is correct.

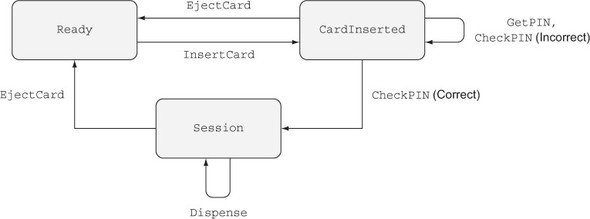
Việc một hoạt động có hợp lệ hay không phụ thuộc vào trạng thái của máy. Ví dụ, thao tác InsertCard chỉ hợp lệ trong trạng thái Ready, vì đó là trạng thái duy nhất mà không có thẻ nào đã được đưa vào máy. Ngoài ra, thao tác Dispense chỉ hợp lệ trong trạng thái Session, vì đó là trạng thái duy nhất có thẻ đã được xác thực trong máy.

Hơn nữa, việc thực hiện một trong những thao tác này có thể thay đổi trạng thái của máy. Ví dụ, InsertCard thay đổi trạng thái từ Ready sang CardInserted, và CheckPIN thay đổi trạng thái từ CardInserted sang Session, với điều kiện mã PIN nhập vào là chính xác.

State machines and types

Hình 1.2 minh họa một máy trạng thái, mô tả cách các thao tác ảnh hưởng đến trạng thái tổng thể của một hệ thống. Máy trạng thái thường hiện diện, một cách ngầm, trong các hệ thống thực tế. Ví dụ, khi bạn mở, đọc, và sau đó đóng một tệp, bạn thay đổi trạng thái của tệp bằng các thao tác mở và đóng. Như bạn sẽ thấy trong chương 13, các kiểu cho phép bạn làm cho những thay đổi trạng thái này trở nên rõ ràng, đảm bảo rằng bạn chỉ thực hiện các thao tác khi chúng hợp lệ, và giúp bạn sử dụng tài nguyên một cách chính xác.

Bằng cách định nghĩa các kiểu chính xác cho từng thao tác trên ATM, bạn có thể đảm bảo, thông qua việc kiểm tra kiểu, rằng ATM chỉ thực hiện các thao tác hợp lệ. Nếu, ví dụ, bạn cố gắng triển khai một chương trình phát tiền mặt mà không xác thực mã PIN, chương trình sẽ không biên dịch. Bằng cách định nghĩa các chuyển trạng thái hợp lệ một cách rõ ràng trong các kiểu, bạn nhận được các đảm bảo mạnh mẽ và có thể kiểm tra bởi máy móc về tính đúng đắn của việc triển khai của chúng. Chúng ta sẽ tìm hiểu về máy trạng thái trong chương 13, và sau đó triển khai ví dụ về ATM trong chương 14.

1.2.3.
Concurrent programming

Một chương trình đồng thời bao gồm nhiều tiến trình chạy cùng lúc và phối hợp với nhau. Các chương trình đồng thời có thể phản hồi và tiếp tục tương tác với người dùng trong khi một phép tính lớn đang được thực hiện. Ví dụ, người dùng có thể tiếp tục duyệt một trang web trong khi một tệp lớn đang được tải xuống. Hơn nữa, bằng cách viết các chương trình đồng thời, chúng ta có thể tận dụng tối đa sức mạnh của bộ xử lý của các CPU hiện đại, chia sẻ công việc giữa nhiều tiến trình trên các lõi CPU khác nhau.

Trong Idris, các tiến trình phối hợp với nhau bằng cách gửi và nhận tin nhắn. Hình 1.3 cho thấy một cách mà điều này có thể hoạt động, với hai tiến trình, main và adder. Tiến trình adder chờ yêu cầu cộng các số từ các tiến trình khác. Sau khi nhận được một tin nhắn từ main yêu cầu nó cộng hai số, nó gửi lại một phản hồi với kết quả.

Figure 1.3.
Two interacting concurrent processes, `main` and `adder`. The `main` process sends a request to `adder`, which then sends a response back to `main`.

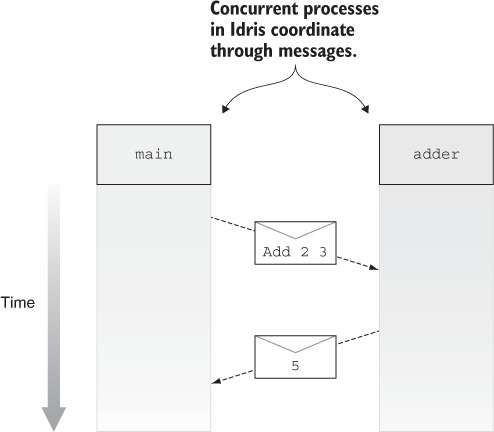
Tuy nhiên, bất chấp những lợi thế của nó, lập trình song song nổi tiếng là dễ mắc lỗi. Sự cần thiết cho các tiến trình tương tác với nhau có thể làm tăng đáng kể độ phức tạp của hệ thống. Đối với mỗi tiến trình, bạn cần đảm bảo rằng các tin nhắn mà nó gửi và nhận được phối hợp đúng cách với các tiến trình khác. Nếu, chẳng hạn, tiến trình chính và tiến trình cộng không được phối hợp đúng cách và mỗi tiến trình đều mong đợi nhận một tin nhắn từ tiến trình còn lại cùng một lúc, chúng sẽ rơi vào tình trạng khóa chết.

Types versus testing for concurrent programs

Kiểm tra một chương trình đồng thời là khó khăn vì, không giống như một chương trình tuần tự hoàn toàn, không có đảm bảo nào về thứ tự mà các phép toán từ các tiến trình khác nhau sẽ được thực hiện. Ngay cả khi hai tiến trình được phối hợp đúng cách khi bạn chạy thử nghiệm một lần, không có đảm bảo rằng chúng sẽ được phối hợp đúng cách khi bạn chạy thử nghiệm lần tiếp theo. Mặt khác, nếu bạn có thể diễn đạt sự phối hợp giữa các tiến trình bằng kiểu, bạn có thể chắc chắn rằng một chương trình đồng thời đã kiểm tra kiểu có các tiến trình được phối hợp đúng cách.

Khi bạn viết các chương trình đồng thời, bạn sẽ lý tưởng có một mô hình về cách các tiến trình nên tương tác. Bằng cách sử dụng kiểu dữ liệu, bạn có thể làm cho mô hình này trở nên rõ ràng trong mã. Sau đó, nếu một chương trình đồng thời được kiểm tra kiểu dữ liệu, bạn sẽ biết rằng nó tuân theo mô hình một cách chính xác. Cụ thể, bạn có thể làm hai điều:

Define an interface for adder that describes the form of messages it will handle.
Define a protocol that defines the order of message passing, ensuring that main will always send a message to adder and then receive a reply, and adder will always do the opposite.

Lập trình đồng thời là một chủ đề rộng lớn, và có nhiều cách mà bạn có thể sử dụng kiểu dữ liệu để mô hình hóa sự phối hợp giữa các tiến trình. Chúng ta sẽ xem xét một ví dụ về cách thực hiện điều này trong chương 15.

1.2.4.
Type, define, refine: the process of type-driven development

Trong từng ví dụ giới thiệu này, chúng ta đã thảo luận về cách chúng ta có thể mô hình hóa một hệ thống: bằng cách mô tả các hình thức hợp lệ của đầu vào và đầu ra cho các phép toán ma trận, các trạng thái hợp lệ của một hệ thống tương tác, hoặc thứ tự truyền tải của các thông điệp giữa các quá trình đồng thời. Trong mỗi trường hợp, để triển khai hệ thống, bạn bắt đầu bằng cách cố gắng tìm một kiểu dữ liệu phản ánh các chi tiết quan trọng của mô hình, và sau đó định nghĩa các hàm để làm việc với kiểu dữ liệu đó, tinh chỉnh kiểu dữ liệu khi cần thiết.

Nói ngắn gọn, bạn có thể mô tả phát triển dựa trên kiểu như một quá trình lặp đi lặp lại của kiểu, định nghĩa, tinh chỉnh: viết một kiểu, triển khai một hàm để thỏa mãn kiểu đó, và tinh chỉnh kiểu hoặc định nghĩa khi bạn hiểu thêm về vấn đề.

Với phép cộng ma trận, ví dụ, bạn thực hiện như sau:

Type— Write a Matrix data type, and use it as the input and output types for an addition function.
Define— Write an addition function that satisfies its input and output types.
Refine— Notice that the input and output types for your addition function allow you to give invalid inputs with different dimensions, and then make the type more precise by including the dimensions of the matrices.

Nói chung, bạn sẽ viết một kiểu để đại diện cho hệ thống mà bạn đang mô hình hóa, định nghĩa các hàm sử dụng kiểu đó, và sau đó tinh chỉnh kiểu và định nghĩa khi cần thiết để nắm bắt bất kỳ thuộc tính nào còn thiếu. Bạn sẽ thấy nhiều hơn về quy trình xác định-định nghĩa-tinh chỉnh này trong suốt cuốn sách này, cả ở quy mô nhỏ khi thực hiện các hàm riêng lẻ, và ở quy mô lớn hơn khi quyết định cách viết các kiểu hàm và dữ liệu.

1.2.5.
Dependent types

Trong ví dụ toán tử ma trận, chúng tôi bắt đầu với kiểu Ma trận và sau đó tinh chỉnh nó để bao gồm số hàng và cột. Điều này có nghĩa là, chẳng hạn, Ma trận 3 4 là kiểu của các ma trận 3 × 4. Trong kiểu này, 3 và 4 là các giá trị thông thường. Một kiểu phụ thuộc, như Ma trận, là một kiểu được tính toán từ một số giá trị khác. Nói cách khác, nó phụ thuộc vào các giá trị khác.

Bằng cách bao gồm các giá trị trong một kiểu như thế này, bạn có thể làm cho các kiểu chính xác như yêu cầu. Chẳng hạn, một số ngôn ngữ có kiểu danh sách đơn giản, mô tả danh sách các đối tượng. Bạn có thể làm cho điều này chính xác hơn bằng cách tham số hóa theo loại phần tử: một danh sách tổng quát các chuỗi chính xác hơn so với một danh sách đơn giản và khác với danh sách các số nguyên. Bạn có thể còn chính xác hơn nữa với kiểu phụ thuộc: một danh sách 4 chuỗi khác với một danh sách 3 chuỗi.

Bảng 1.2 minh họa cách các kiểu trong Idris có thể có các mức độ chính xác khác nhau ngay cả đối với các phép toán cơ bản như nối danh sách. Giả sử bạn có hai danh sách chuỗi cụ thể đầu vào:

["a", "b", "c", "d"] ["e", "f", "g"]

Table 1.2.
Appending specific typed lists. Unlike simple types, where there’s no difference between the input and output list types, dependent types allow the length to be encoded in the type.

	Nhập ["a", "b", "c", "d"]	Nhập ["e", "f", "g"]	Loại đầu ra
Simple	AnyList	AnyList	AnyList
Generic	List String	List String	List String
Dependent	Vect 4 String	Vect 3 String	Vect 7 String

Khi bạn ghép chúng lại, bạn sẽ mong đợi danh sách đầu ra sau:

["a", "b", "c", "d", "e", "f", "g"]

Sử dụng một kiểu đơn giản, cả hai danh sách đầu vào đều có kiểu AnyList, cũng như danh sách đầu ra. Sử dụng một kiểu tổng quát, bạn có thể chỉ ra rằng cả hai danh sách đầu vào đều là danh sách các chuỗi, cũng như danh sách đầu ra. Các kiểu chính xác hơn có nghĩa là, ví dụ, đầu ra rõ ràng có liên quan đến đầu vào ở chỗ kiểu phần tử không thay đổi. Cuối cùng, sử dụng một kiểu phụ thuộc, bạn có thể xác định kích thước của các danh sách đầu vào và đầu ra. Rõ ràng từ kiểu rằng độ dài của danh sách đầu ra là tổng của độ dài của các danh sách đầu vào. Nghĩa là, một danh sách gồm 3 chuỗi được nối với một danh sách gồm 4 chuỗi sẽ tạo ra một danh sách có 7 chuỗi.

Lists and vectors

Cú pháp cho các kiểu trong bảng 1.2 là cú pháp hợp lệ của Idris. Idris cung cấp nhiều cách để xây dựng các kiểu danh sách, với các mức độ chính xác khác nhau. Trong bảng, bạn có thể thấy hai trong số đó, List và Vect. AnyList được đưa vào bảng chỉ để minh họa và không được định nghĩa trong Idris. List mã hóa các danh sách tổng quát mà không có độ dài rõ ràng, trong khi Vect (viết tắt của "vector") mã hóa các danh sách với độ dài rõ ràng trong kiểu. Bạn sẽ thấy nhiều hơn về cả hai kiểu này trong suốt cuốn sách này.

Bảng 1.3 minh họa cách mà các kiểu đầu vào và đầu ra của một hàm thêm có thể được viết với các mức độ chính xác tăng dần trong Idris. Sử dụng các kiểu đơn giản, bạn có thể viết các kiểu đầu vào và đầu ra là AnyList, điều này gợi ý rằng bạn không quan tâm đến các kiểu của các phần tử trong danh sách. Sử dụng các kiểu tổng quát, bạn có thể viết các kiểu đầu vào và đầu ra là List elem. Ở đây, elem là một biến kiểu đứng cho các kiểu phần tử. Bởi vì biến kiểu là giống nhau cho cả hai đầu vào và đầu ra, các kiểu này chỉ định rằng cả các danh sách đầu vào và danh sách đầu ra đều có kiểu phần tử nhất quán. Nếu bạn nối hai danh sách số nguyên, các kiểu đảm bảo rằng đầu ra cũng sẽ là một danh sách số nguyên. Cuối cùng, sử dụng các kiểu phụ thuộc, bạn có thể viết các đầu vào là Vect n elem và Vect m elem, trong đó n và m là các biến đại diện cho độ dài của mỗi danh sách. Kiểu đầu ra chỉ định rằng độ dài kết quả sẽ là tổng của độ dài của các đầu vào.

Table 1.3.
Appending typed lists, in general. Type variables describe the relationships between the inputs and outputs, even though the exact inputs and outputs are unknown.

	Nhập loại 1	Nhập 2 loại	Loại đầu ra
Simple	AnyList	AnyList	AnyList
Generic	List elem	List elem	List elem
Dependent	Vect n elem	Vect m elem	Vect (n + m) elem

Type variables

Các kiểu thường chứa biến kiểu, như n, m và elem trong bảng 1.3. Chúng rất giống với các tham số của kiểu tổng quát trong Java hoặc C#, nhưng chúng phổ biến đến mức trong Idris, chúng có cú pháp rất nhẹ. Nói chung, tên kiểu cụ thể bắt đầu bằng một chữ cái in hoa, và tên biến kiểu bắt đầu bằng một chữ cái in thường.

Trong kiểu phụ thuộc cho hàm nối trong bảng 1.3, các tham số n và m là các giá trị số thông thường, và toán tử + là toán tử cộng bình thường. Tất cả những điều này có thể xuất hiện trong các chương trình giống như chúng đã xuất hiện ở đây trong các kiểu dữ liệu.

Introductory exercises

Trong suốt cuốn sách này, các bài tập sẽ giúp củng cố các khái niệm mà bạn đã học. Là một sự khởi động, hãy xem xét tập hợp các đặc tả hàm sau đây, được đưa ra hoàn toàn dưới dạng các loại đầu vào và đầu ra. Đối với mỗi đặc tả, hãy gợi ý các phép toán có thể thỏa mãn các loại đầu vào và đầu ra đã cho. Lưu ý rằng có thể có nhiều hơn một câu trả lời trong mỗi trường hợp.

Input type: Vect n elem Output type: Vect n elem
Input type: Vect n elem Output type: Vect (n * 2) elem
Input type: Vect (1 + n) elem Output type: Vect n elem
Assume that Bounded n represents a number between zero and n - 1. Input types: Bounded n, Vect n elem Output type: elem

1.3. Pure functional programming

Idris là một ngôn ngữ lập trình hàm tinh khiết, vì vậy trước khi chúng ta bắt đầu khám phá Idris một cách sâu sắc, chúng ta nên xem xét ý nghĩa của việc một ngôn ngữ là hàm và khái niệm thuần khiết. Thật không may, không có định nghĩa được đồng thuận rộng rãi về chính xác ý nghĩa của một ngôn ngữ lập trình là hàm, nhưng cho mục đích của chúng ta, chúng ta sẽ hiểu nó như sau:

Programs are composed of functions.
Program execution consists of the evaluation of functions.
Functions are a first-class language construct.

Điều này khác với ngôn ngữ lập trình mệnh lệnh chủ yếu ở chỗ lập trình hàm quan tâm đến việc đánh giá các hàm, chứ không phải thực thi các câu lệnh.

Trong một ngôn ngữ hàm thuần túy, các điều sau đây cũng đúng:

Functions don’t have side effects such as modifying global variables, throwing exceptions, or performing console input or output.
As a result, for any specific inputs, a function will always give the same result.

Bạn có thể tự hỏi, rất hợp lý, làm thế nào có thể viết phần mềm hữu ích nào dưới những ràng buộc này. Thực tế, hoàn toàn không làm cho việc viết các chương trình thực tế trở nên khó khăn hơn, lập trình hàm thuần túy cho phép bạn đối xử với những khái niệm khó khăn như trạng thái và ngoại lệ một cách nghiêm túc như chúng xứng đáng. Hãy cùng khám phá thêm.

1.3.1.
Purity and referential transparency

Tính chất chính của một hàm thuần túy là các đầu vào giống nhau luôn tạo ra kết quả giống nhau. Tính chất này được gọi là tính minh bạch tham chiếu. Một biểu thức (như một lời gọi hàm) trong một hàm được xem là minh bạch tham chiếu nếu nó có thể được thay thế bằng kết quả của nó mà không làm thay đổi hành vi của hàm. Nếu các hàm chỉ sản xuất kết quả, mà không có tác dụng phụ, thì tính chất này rõ ràng là đúng. Tính minh bạch tham chiếu là một khái niệm rất hữu ích trong phát triển dựa trên kiểu, vì nếu một hàm không có tác dụng phụ và hoàn toàn được xác định bởi các đầu vào và đầu ra của nó, thì bạn có thể xem xét các kiểu dữ liệu đầu vào và đầu ra của nó và có một ý tưởng rõ ràng về giới hạn của những gì hàm có thể làm.

Hình 1.4 cho thấy các ví dụ về đầu vào và đầu ra cho hàm append. Nó nhận hai đầu vào và tạo ra một kết quả, nhưng không có tương tác với người dùng, chẳng hạn như đọc từ bàn phím, và không có đầu ra thông tin, chẳng hạn như ghi log hay thanh tiến trình.

Figure 1.4.
A pure function, taking inputs and producing outputs with no observable side effects

Hình 1.5 cho thấy các hàm thuần túy một cách tổng quát. Không thể có bất kỳ tác động phụ nào có thể quan sát được khi chạy những chương trình này, ngoại trừ có thể làm cho máy tính ấm hơn một chút hoặc mất một khoảng thời gian khác nhau để chạy.

Figure 1.5.
Pure functions, in general, take only inputs and have no observable side effects.

Các hàm thuần túy rất phổ biến trong thực tế, đặc biệt là trong việc xây dựng và xử lý các cấu trúc dữ liệu. Có thể lý luận về hành vi của chúng vì hàm luôn trả về cùng một kết quả cho cùng một đầu vào; những hàm này là các thành phần quan trọng trong các chương trình lớn hơn. Hàm append trước đó là hàm thuần túy, và nó là một thành phần quý giá cho bất kỳ chương trình nào làm việc với danh sách. Nó tạo ra một danh sách như là kết quả, và vì nó là thuần túy, bạn biết rằng nó sẽ không yêu cầu bất kỳ đầu vào nào, không ghi bất kỳ thông tin nào, hoặc không thực hiện bất kỳ hành động phá hủy nào như xóa tệp.

1.3.2.
Side-effecting programs

Một cách thực tế, các chương trình cần phải có tác dụng phụ để có thể hữu ích, và bạn sẽ luôn phải đối mặt với những đầu vào không mong đợi hoặc sai lầm trong phần mềm thực tiễn. Ban đầu, điều này có vẻ không thể xảy ra trong một ngôn ngữ thuần khiết. Tuy nhiên, có một cách: các hàm thuần khiết có thể không thực hiện được tác dụng phụ, nhưng chúng có thể mô tả chúng.

Xem xét một hàm đọc hai danh sách từ một tệp, gộp chúng lại, in danh sách kết quả và trả về nó. Dưới đây là mô tả của hàm này bằng pseudocode theo phong cách mệnh lệnh, sử dụng các kiểu đơn giản.

Listing 1.1.
Appending lists read from a file (pseudocode)

List appendFromFile(File h) { list1 = readListFrom(h) list2 = readListFrom(h) result = append(list1, list2) print(result) return result }

Chương trình này nhận một tay điều khiển tệp làm đầu vào và trả về một danh sách với một số tác động phụ. Nó đọc hai danh sách từ tệp đã cho và in ra danh sách trước khi trả về. Hình 1.6 minh họa điều này cho trường hợp khi tệp chứa hai danh sách ["a", "b", "c", "d"] và ["e", "f", "g"].

Figure 1.6.
A side-effecting program, reading inputs from a file, printing the result, and returning the result

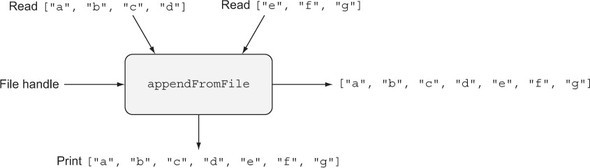
Hàm appendFromFile không thỏa mãn thuộc tính trong suốt tham chiếu. Trong suốt tham chiếu yêu cầu rằng một biểu thức có thể được thay thế bằng kết quả của nó mà không làm thay đổi hành vi của chương trình. Tuy nhiên, ở đây, việc thay thế một lời gọi đến appendFromFile bằng kết quả của nó có nghĩa là sẽ không có gì được đọc từ tệp và không có gì được xuất ra màn hình. Các kiểu đầu vào và đầu ra của hàm cho chúng ta biết rằng đầu vào là một tệp và đầu ra là một danh sách, nhưng không có gì trong kiểu này mô tả các hiệu ứng phụ mà hàm có thể thực hiện.

Trong lập trình hàm thuần túy nói chung, và Idris nói riêng, bạn có thể giải quyết vấn đề này bằng cách viết các hàm mô tả các hiệu ứng phụ, thay vì các hàm thực thi chúng, và ủy quyền chi tiết thực thi cho trình biên dịch và hệ thống thời gian chạy. Chúng ta sẽ khám phá điều này một cách chi tiết hơn trong chương 5; hiện tại, đủ để nhận ra rằng một chương trình có hiệu ứng phụ có một kiểu dữ liệu làm rõ điều này. Ví dụ, có sự phân biệt giữa các trường hợp sau:

String is the type of a program that results in a String and is guaranteed to perform no input or output as side effects.
IO String is the type of a program that describes a sequence of input and output operations that result in a String.

Phát triển dựa trên kiểu (Type-driven development) đã mở rộng ý tưởng này xa hơn nữa. Như bạn sẽ thấy từ chương 12 trở đi, bạn có thể định nghĩa các kiểu mà mô tả các tác dụng phụ cụ thể mà một chương trình có thể có, chẳng hạn như tương tác với console, đọc và ghi trạng thái toàn cục, hoặc khởi động các tiến trình đồng thời và gửi tin nhắn.

1.3.3.
Partial and total functions

Idris hỗ trợ một thuộc tính mạnh mẽ hơn cả tính thuần khiết cho các hàm, tạo ra sự phân biệt giữa hàm toàn phần và hàm từng phần. Hàm toàn phần được đảm bảo sẽ sản xuất một kết quả, có nghĩa là nó sẽ trả về một giá trị trong thời gian hữu hạn cho mọi đầu vào hợp kiểu có thể và được đảm bảo không ném ra bất kỳ ngoại lệ nào. Ngược lại, hàm từng phần có thể không trả về kết quả cho một số đầu vào. Dưới đây là một vài ví dụ:

The append function is total for finite lists, because it will always return a new list.
The function that returns the first element of a list is partial, because it’s not defined if the list is empty, and it will therefore crash.

Total functions and long-running programs

Một hàm tổng quát đảm bảo tạo ra một tiền tố hữu hạn của một kết quả có thể vô hạn. Như bạn sẽ thấy trong chương 11, bạn có thể viết các shell lệnh hoặc máy chủ dưới dạng các hàm tổng quát đảm bảo một phản hồi cho mỗi đầu vào của người dùng, vô thời hạn.

Sự phân biệt này rất quan trọng vì việc biết rằng một hàm là tổng thể cho phép bạn đưa ra nhiều tuyên bố mạnh mẽ hơn về hành vi của nó dựa trên loại của nó. Nếu bạn có một hàm với kiểu trả về là String, ví dụ, bạn có thể đưa ra những tuyên bố khác nhau tùy thuộc vào việc hàm đó là riêng lẻ hay tổng thể.

If it’s total— It will return a value of type String in finite time.
If it’s partial— If it doesn’t crash or enter an infinite loop, the value it returns will be a String.

Trong hầu hết các ngôn ngữ hiện đại, chúng ta phải giả định rằng các hàm là từng phần và do đó chỉ có thể đưa ra yêu cầu yếu hơn đó. Idris kiểm tra xem các hàm có toàn phần hay không, vì vậy chúng ta thường có thể đưa ra yêu cầu mạnh mẽ hơn đó.

Total functions and the halting problem

Vấn đề dừng (halting problem) là bài toán xác định xem một chương trình có kết thúc cho một đầu vào cụ thể hay không. Nhờ có Alan Turing, chúng ta biết rằng không thể viết một chương trình giải quyết vấn đề dừng một cách tổng quát. Với điều này, thật hợp lý khi tự hỏi làm thế nào Idris có thể xác định rằng một hàm là tổng quát, mà thực chất là kiểm tra xem hàm đó có kết thúc cho tất cả các đầu vào hay không.

Mặc dù nó không thể giải quyết vấn đề một cách tổng quát, Idris có thể xác định một lớp lớn các hàm chắc chắn là tổng quát. Bạn sẽ tìm hiểu thêm về cách nó thực hiện điều đó, cùng với một số kỹ thuật để viết các hàm tổng quát, trong các chương 10 và 11.

Một mẫu hữu ích trong phát triển dựa trên loại là viết một kiểu mà mô tả chính xác các trạng thái hợp lệ của một hệ thống (như máy ATM trong phần 1.2.2) và hạn chế các phép toán mà hệ thống được phép thực hiện. Một hàm tổng quát với kiểu đó sẽ được bộ kiểm tra kiểu đảm bảo thực hiện các phép toán đó một cách chính xác như kiểu yêu cầu.

1.4. A quick tour of Idris

Hệ thống Idris bao gồm một môi trường tương tác và một trình biên dịch chế độ hàng loạt. Trong môi trường tương tác, bạn có thể tải và kiểm tra kiểu của các tệp nguồn, đánh giá biểu thức, tìm kiếm thư viện, duyệt tài liệu, và biên dịch cũng như chạy các chương trình hoàn chỉnh. Chúng tôi sẽ sử dụng những tính năng này một cách rộng rãi trong suốt cuốn sách này.

Trong phần này, tôi sẽ giới thiệu ngắn gọn các tính năng quan trọng nhất của môi trường, đó là đánh giá và kiểm tra kiểu, và mô tả cách biên dịch và chạy các chương trình Idris. Tôi cũng sẽ giới thiệu hai tính năng đặc trưng nhất của ngôn ngữ Idris.

Holes, which stand for incomplete programs
The use of types as first-class language constructs

Như bạn sẽ thấy, bằng cách sử dụng các lỗ hổng, bạn có thể định nghĩa các hàm một cách từng bước, yêu cầu trình kiểm tra kiểu cung cấp thông tin ngữ cảnh để giúp hoàn thiện các định nghĩa. Bằng cách sử dụng các kiểu đầu tiên, bạn có thể rất chính xác về những gì một hàm dự định thực hiện, và thậm chí yêu cầu trình kiểm tra kiểu điền vào một số chi tiết của các hàm cho bạn.

1.4.1.
The interactive environment

Phần lớn tương tác của bạn với Idris sẽ thông qua một môi trường tương tác gọi là vòng lặp đọc-đánh giá-in, thường được viết tắt là REPL. Như tên gọi gợi ý, REPL sẽ đọc đầu vào từ người dùng, thường dưới dạng biểu thức, đánh giá biểu thức và sau đó in kết quả.

Khi Idris đã được cài đặt, bạn có thể bắt đầu REPL bằng cách gõ idris tại dấu nhắc shell. Bạn sẽ thấy một cái gì đó giống như sau:

 ____ __ _ / _/___/ /____(_)____ / // __ / ___/ / ___/ Version 1.0 _/ // /_/ / / / (__ ) http://www.idris-lang.org/ /___/\__,_/_/ /_/____/ Type :? for help Idris is free software with ABSOLUTELY NO WARRANTY. For details type :warranty. Idris>

Installing Idris

Bạn có thể tìm thấy hướng dẫn về cách tải xuống và cài đặt Idris cho Linux, OS X hoặc Windows trong phụ lục A.

Bạn có thể nhập các biểu thức để được đánh giá tại dấu nhắc Idris>. Ví dụ, các biểu thức số học hoạt động theo cách thông thường, với các quy tắc ưu tiên thường gặp (tức là, * và / có ưu tiên cao hơn + và -):

Idris> 2 + 2 4 : Integer Idris> 2.1 * 20 42.0 : Double Idris> 6 + 8 * 11 94 : Integer

Bạn cũng có thể thao tác với chuỗi. Toán tử ++ nối chuỗi, và hàm reverse đảo ngược một chuỗi:

Idris> "Hello" ++ " " ++ "World!" "Hello World!" : String Idris> reverse "abcdefg" "gfedcba" : String

Lưu ý rằng Idris không chỉ in kết quả của việc đánh giá biểu thức mà còn in cả kiểu của nó. Nói chung, nếu bạn thấy một cái gì đó có dạng x : T—một biểu thức x, một dấu hai chấm, và một biểu thức khác T—có thể đọc là “x có kiểu T.” Trong các ví dụ trước, bạn có những điều sau:

4 has type Integer.
42.0 has type Double.
"Hello World!" has type String.

1.4.2.
Checking types

REPL cung cấp một số lệnh, tất cả đều được bắt đầu bằng dấu hai chấm. Một trong những lệnh hữu ích nhất là :t, cho phép bạn kiểm tra các kiểu của biểu thức mà không cần đánh giá chúng:

Idris> :t 2 + 2 2 + 2 : Integer Idris> :t "Hello!" "Hello!" : String

Các kiểu, chẳng hạn như Integer và String, có thể được thao tác giống như bất kỳ giá trị nào khác, vì vậy bạn cũng có thể kiểm tra loại của chúng.

Idris> :t Integer Integer : Type Idris> :t String String : Type

Thật tự nhiên khi tự hỏi kiểu của Type bản thân có thể là gì. Trong thực tế, bạn sẽ không bao giờ cần phải lo lắng về điều này, nhưng vì lý do đầy đủ, hãy cùng xem xét:

Idris> :t Type Type : Type 1

Nói cách khác, Type có kiểu Type 1, Type 1 có kiểu Type 2, và cứ tiếp tục như vậy mãi mãi, theo như chúng tôi quan tâm. Tin tốt là Idris sẽ lo liệu các chi tiết cho bạn, và bạn luôn có thể viết Type một mình.

1.4.3.
Compiling and running Idris programs

Cũng như việc đánh giá biểu thức và kiểm tra loại của các hàm, bạn sẽ muốn có khả năng biên dịch và chạy các chương trình hoàn chỉnh. Danh sách sau đây cho thấy một chương trình Idris tối thiểu.

Listing 1.2.
Hello, Idris World! (Hello.idr)

Vào thời điểm này, bạn không cần quá lo lắng về cú pháp hay cách chương trình hoạt động. Hiện tại, bạn chỉ cần biết rằng các tệp nguồn Idris bao gồm một tiêu đề module và một tập hợp các định nghĩa hàm và kiểu dữ liệu. Chúng cũng có thể nhập khẩu các tệp nguồn khác.

Whitespace significance

Khoảng trắng là quan trọng trong Idris, vì vậy khi bạn gõ danh sách 1.2, hãy chắc chắn rằng không có khoảng trắng ở đầu mỗi dòng.

Ở đây, mô-đun được gọi là Main, và chỉ có một định nghĩa hàm, gọi là main. Điểm vào của bất kỳ chương trình Idris nào là hàm main trong mô-đun Main.

Để chạy chương trình, hãy làm theo các bước sau:

Create a file called Hello.idr in a text editor.^[1] Idris source files all have the extension .idr.

Sure, please provide the content you would like to have translated into Vietnamese.
I recommend Atom because it has a mode for interactive editing of Idris programs, which we’ll use in this book.
Enter the code in listing 1.2.
In the working directory where you saved Hello.idr, start up an Idris REPL with the command idris Hello.idr.
At the Idris prompt, type :exec.

Nếu mọi thứ ổn, bạn sẽ thấy một cái gì đó giống như sau:

$ idris Hello.idr ____ __ _ / _/___/ /____(_)____ / // __ / ___/ / ___/ Version 1.0 _/ // /_/ / / / (__ ) http://www.idris-lang.org/ /___/\__,_/_/ /_/____/ Type :? for help Idris is free software with ABSOLUTELY NO WARRANTY. For details type :warranty. Type checking ./Hello.idr *Hello> :exec Hello, Idris World

Ở đây, $ đại diện cho dấu nhắc shell của bạn. Ngoài ra, bạn có thể tạo một tệp thực thi độc lập bằng cách gọi lệnh idris với tùy chọn -o, như sau:

$ idris Hello.idr -o Hello $ ./Hello Hello, Idris World

The REPL prompt

Nhắc nhở REPL, theo mặc định, cho bạn biết tên của tệp hiện đang được tải. Nhắc nhở Idris> cho biết rằng chưa có tệp nào được tải, trong khi nhắc nhở *Hello> chỉ ra rằng tệp Hello.idr đã được tải.

1.4.4.
Incomplete definitions: working with holes

Trước đó, tôi đã so sánh việc làm việc với kiểu và giá trị giống như việc đưa các hình dạng vào một món đồ chơi phân loại hình. Cũng giống như hình vuông chỉ có thể lọt qua lỗ vuông, đối số "Hello, Idris World!" chỉ có thể fit vào một hàm ở nơi mà một kiểu String được mong đợi.

Các hàm Idris có thể chứa lỗ hổng, và một hàm có lỗ hổng là chưa hoàn chỉnh. Chỉ có giá trị của loại thích hợp mới phù hợp với lỗ hổng, giống như một hình vuông chỉ có thể vừa vặn vào một lỗ vuông trong bộ phân loại hình dạng. Dưới đây là một triển khai chưa hoàn chỉnh của chương trình "Xin chào, Thế giới Idris!"

Nếu bạn chỉnh sửa tệp Hello.idr để thay thế chuỗi "Hello, Idris World!" bằng ?greeting và tải nó vào REPL của Idris, bạn sẽ thấy một cái gì đó giống như sau:

Type checking ./Hello.idr Holes: Main.greeting *Hello>

Cú pháp ?greeting giới thiệu một lỗ hỏng, là một phần của chương trình chưa được viết. Bạn có thể kiểm tra kiểu của các chương trình có lỗ hỏng và đánh giá chúng tại REPL.

Ở đây, khi Idris gặp lỗ chào, nó tạo ra một tên mới, greeting, có kiểu nhưng không có định nghĩa. Bạn có thể kiểm tra kiểu bằng cách sử dụng :t tại REPL:

*Hello> :t greeting -------------------------------------- greeting : String

Nếu bạn cố gắng đánh giá nó, ngược lại, Idris sẽ cho bạn thấy đó là một cái lỗ:

*Hello> greeting ?greeting : String

Reloading

Thay vì thoát khỏi REPL và khởi động lại, bạn cũng có thể nạp lại Hello.idr bằng lệnh REPL :r như sau:

*Hello> :r Type checking ./Hello.idr Holes: Main.greeting *Hello>

Các lỗ hổng cho phép bạn phát triển chương trình một cách tuần tự, viết những phần bạn biết và nhờ máy giúp bạn xác định các kiểu cho những phần bạn không biết. Ví dụ, giả sử bạn muốn in một ký tự (có kiểu Char) thay vì một chuỗi String. Hàm putStrLn yêu cầu một đối số kiểu String, vì vậy bạn không thể đơn giản truyền một Char cho nó.

Listing 1.3.
A program with a type error

"Nếu bạn thử tải chương trình này vào REPL, Idris sẽ báo lỗi:"

Hello.idr:4:17:When checking right hand side of main: When checking an application of function Prelude.putStrLn: Type mismatch between Char (Type of 'x') and String (Expected type)

Bạn phải chuyển một ký tự thành chuỗi bằng cách nào đó. Ngay cả khi bạn không biết chính xác cách thực hiện điều này lúc đầu, bạn có thể bắt đầu bằng cách thêm một ô trống để thay thế cho việc chuyển đổi.

module Main main : IO () main = putStrLn (?convert 'x')

Sau đó, bạn có thể kiểm tra loại lỗ chuyển đổi:

Loại của lỗ, Char -> String, là loại của một hàm nhận vào một Char và trả ra một String. Chúng ta sẽ thảo luận về chuyển đổi kiểu một cách chi tiết hơn trong chương 2, nhưng một hàm phù hợp để hoàn thành định nghĩa này là cast:

main : IO () main = putStrLn (cast 'x')

1.4.5.
First-class types

Một cấu trúc ngôn ngữ hạng nhất là cấu trúc được coi là một giá trị, không có hạn chế cú pháp về nơi nó có thể được sử dụng. Nói cách khác, một cấu trúc hạng nhất có thể được truyền cho các hàm, trả về từ các hàm, lưu trữ trong các biến, và những thứ tương tự.

Trong hầu hết các ngôn ngữ kiểu tĩnh, có những hạn chế về nơi mà kiểu có thể được sử dụng, và có sự phân tách cú pháp nghiêm ngặt giữa kiểu và giá trị. Bạn không thể, ví dụ, nói x = int trong thân của một phương thức Java hoặc một hàm C. Trong Idris, không có những hạn chế như vậy, và kiểu là loại đầu tiên; không chỉ kiểu có thể được sử dụng theo cách giống như bất kỳ cấu trúc ngôn ngữ nào khác, mà bất kỳ cấu trúc nào cũng có thể xuất hiện như một phần của kiểu.

Điều này có nghĩa là bạn có thể viết các hàm tính toán kiểu, và kiểu trả về của một hàm có thể khác nhau tùy thuộc vào giá trị đầu vào của hàm. Ý tưởng này thường xuất hiện khi lập trình trong Idris, và có nhiều tình huống thực tế mà nó hữu ích:

A database schema determines the allowed forms of queries on a database.
A form on a web page determines the number and type of inputs expected.
A network protocol description determines the types of values that can be sent or received over a network.

Trong mỗi trường hợp này, một mảnh dữ liệu nói cho bạn biết về hình thức dự kiến của một số dữ liệu khác. Nếu bạn đã lập trình bằng C, bạn sẽ thấy một ý tưởng tương tự với hàm printf, trong đó một đối số là chuỗi định dạng mô tả số lượng và các kiểu dữ liệu dự kiến của những đối số còn lại. Hệ thống kiểu dữ liệu C không thể kiểm tra rằng chuỗi định dạng nhất quán với các đối số, vì vậy kiểm tra này thường được mã cứng vào các trình biên dịch C. Tuy nhiên, trong Idris, bạn có thể viết một hàm tương tự như printf trực tiếp, bằng cách tận dụng các kiểu dữ liệu như các cấu trúc hạng nhất. Bạn sẽ thấy ví dụ cụ thể này trong chương 6.

Danh sách sau minh họa khái niệm kiểu hạng nhất với một ví dụ nhỏ: tính toán một kiểu từ một đầu vào Boolean.

Listing 1.4.
Calculating a type, given a Boolean value (FCTypes.idr)

Function syntax

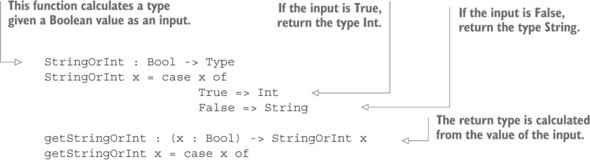
Chúng ta sẽ đi vào chi tiết hơn về cú pháp Idris trong các chương tới. Hiện tại, hãy chỉ ghi nhớ những điều sau:

A function type takes the form a -> b -> ... -> t, where a, b, and so on, are the input types, and t is the output type. Inputs may also be annotated with names, taking the form (x : a) -> (y : b) -> ... -> t.
name : type declares a new function, name, of type type.
Functions are defined by equations: square x = x * x

Điều này định nghĩa một hàm gọi là square mà nhân đầu vào của nó với chính nó.

Ở đây, StringOrInt là một hàm tính toán một kiểu dữ liệu. Liệt kê 1.4 sử dụng nó theo hai cách:

In getStringOrInt, StringOrInt calculates the return type. If the input is True, getStringOrInt returns an Int; otherwise it returns a String.
In valToString, StringOrInt calculates an argument type. If the first input is True, the second input must be an Int; otherwise it must be a String.

Bạn có thể thấy chi tiết những gì đang diễn ra bằng cách giới thiệu các lỗ hổng trong định nghĩa của valToString:

valToString : (x : Bool) -> StringOrInt x -> String valToString x val = case x of True => ?xtrueType False => ?xfalseType

Kiểm tra kiểu của một lỗ với :t không chỉ cung cấp kiểu của chính lỗ đó, mà còn cả kiểu của bất kỳ biến cục bộ nào trong phạm vi. Nếu bạn kiểm tra kiểu của xtrueType, bạn sẽ thấy kiểu của val, được tính toán khi x được biết là True:

*FCTypes> :t xtrueType x : Bool val : Int -------------------------------------- xtrueType : String

Vì vậy, nếu x là True, thì val phải là một Int, như được tính toán bởi hàm StringOrInt. Tương tự, bạn có thể kiểm tra kiểu của xfalseType để xem kiểu của val khi x được biết là False:

*FCTypes> :t xfalseType x : Bool val : String -------------------------------------- xfalseType : String

Đây là một ví dụ nhỏ, nhưng nó minh họa một khái niệm cơ bản của phát triển theo kiểu và lập trình với các kiểu phụ thuộc: ý tưởng rằng kiểu của một biến có thể được tính toán từ giá trị của một biến khác. Trong mỗi trường hợp, Idris đã sử dụng StringOrInt để tinh chỉnh kiểu của val, dựa trên những gì nó biết về giá trị của x.

1.5. Summary

Types are a means of classifying values. Programming languages use types to decide how to lay out data in memory, and to ensure that data is interpreted consistently.
A type can be viewed as a specification, so that a language implementation (specifically, its type checker) can check whether a program conforms to that specification.
Type-driven development is an iterative process of type, define, refine, creating a type to model a system, then defining functions, and finally refining the types as necessary.
In type-driven development, a type is viewed more like a plan, helping an interactive environment guide the programmer to a working program.
Dependent types allow you to give more-precise types to programs, and hence more informative plans to the machine.
In a functional programming language, program execution consists of evaluating functions.
In a purely functional programming language, additionally, functions have no side effects.
Instead of writing programs that perform side effects, you can write programs that describe side effects, with the side effects stated explicitly in a program’s type.
A total function is guaranteed to produce a result for any well-typed input in finite time.
Idris is a programming language that’s specifically designed to support type-driven development. It’s a purely functional programming language with first-class dependent types.
Idris allows programs to contain holes that stand for incomplete programs.
In Idris, types are first-class, meaning that they can be stored in variables, passed to functions, or returned from functions like any other value.

Chapter 2.
Getting started with Idris

Chương này đề cập đến

Using built-in types and functions
Defining functions
Structuring Idris programs

Khi học bất kỳ ngôn ngữ mới nào, việc nắm vững những kiến thức cơ bản trước khi chuyển sang các đặc điểm nổi bật hơn của ngôn ngữ là rất quan trọng. Với điều này trong tâm trí, trước khi chúng ta bắt đầu khám phá các loại phụ thuộc và phát triển dựa trên loại, chúng ta sẽ xem qua một số kiểu và giá trị mà bạn sẽ thấy quen thuộc từ các ngôn ngữ khác, và bạn sẽ thấy chúng hoạt động như thế nào trong Idris. Bạn cũng sẽ thấy cách định nghĩa hàm và kết hợp chúng lại để xây dựng một chương trình Idris hoàn chỉnh, mặc dù đơn giản.

Nếu bạn đã quen thuộc với một ngôn ngữ lập trình thuần chức năng, đặc biệt là Haskell, thì phần lớn chương này sẽ rất quen thuộc với bạn. Danh sách 2.1 trình bày một chương trình Idris đơn giản, nhưng tự chứa, yêu cầu nhập liệu từ console và sau đó hiển thị độ dài trung bình của các từ trong đầu vào. Nếu bạn đã thoải mái khi đọc chương trình này với sự trợ giúp của các chú thích, bạn có thể an tâm bỏ qua chương này, vì nó cố ý không giới thiệu bất kỳ đặc điểm ngôn ngữ nào cụ thể cho Idris. Dù vậy, tôi vẫn khuyên bạn nên lướt qua các mẹo và ghi chú trong chương này và đọc tóm tắt ở cuối để đảm bảo rằng không có chi tiết nhỏ nào bạn đã bỏ lỡ.

Please provide the text you would like to have translated into Vietnamese.
Comparing Idris to Haskell, the most important difference is that Idris doesn’t use lazy evaluation by default.

Nếu không, đừng lo lắng. Đến cuối chương này, chúng ta sẽ đề cập đến tất cả các tính năng cần thiết để bạn có thể tự thực hiện các chương trình tương tự.

Listing 2.1.
A complete Idris program to calculate average word length (Average.idr)

2.1. Basic types

Idris cung cấp một số kiểu cơ bản và hàm tiêu chuẩn để làm việc với các dạng, ký tự và chuỗi khác nhau. Trong phần này, tôi sẽ cung cấp cho bạn một cái nhìn tổng quan về những thứ này, kèm theo một số ví dụ. Những kiểu cơ bản này được định nghĩa trong Prelude, là một tập hợp các kiểu và hàm tiêu chuẩn được tự động nhập khẩu bởi mọi chương trình Idris.

Tôi sẽ cho bạn thấy một số biểu thức ví dụ trong phần này, và có thể bạn sẽ thấy khá rõ ràng chúng nên thực hiện những gì. Tuy nhiên, thay vì chỉ đọc chúng và gật đầu, tôi rất khuyên bạn nên gõ các ví dụ vào REPL của Idris. Bạn sẽ học cú pháp dễ dàng hơn nhiều bằng cách sử dụng nó hơn là chỉ đọc nó.

Trên đường đi, chúng ta cũng sẽ gặp một vài tính năng hữu ích của REPL cho phép chúng ta lưu trữ kết quả của các phép tính tại REPL.

The Prelude

Các loại và hàm mà tôi sẽ thảo luận được định nghĩa trong Prelude. Prelude là thư viện tiêu chuẩn của Idris, luôn có sẵn trong REPL và được tự động nhập bởi mọi chương trình Idris. Với ngoại lệ của một số loại nguyên thủy và thao tác, mọi thứ trong Prelude đều được viết bằng chính Idris.

2.1.1.
Numeric types and values

Idris cung cấp một số loại số cơ bản, bao gồm các loại sau:

Int—A fixed-width signed integer type. It’s guaranteed to be at least 31 bits wide, but the exact width is system dependent.
Integer—An unbounded signed integer type. Unlike Int, there’s no limit to the size of the numbers that can be represented, other than your machine’s memory, but this type is more expensive in terms of performance and memory usage.
Nat—An unbounded unsigned integer type. This is very often used for sizes and indexing of data structures, because they can never be negative. You’ll see much more of Nat later.
Double—A double-precision floating-point type.

Subtraction with Nats

Bởi vì Nat không bao giờ có thể âm, một Nat chỉ có thể được trừ từ một Nat lớn hơn.

Chúng ta có thể sử dụng các hằng số số chuẩn làm giá trị cho mỗi loại này. Ví dụ, hằng số 333 có thể thuộc loại Int, Integer, Nat hoặc Double. Hằng số 333.0 chỉ có thể thuộc loại Double, do có dấu chấm thập phân rõ ràng.

Bạn có thể thử một số phép tính đơn giản tại REPL:

Idris> 6 + 3 * 12 42 : Integer Idris> 6.0 + 3 * 12 42.0 : Double

Lưu ý rằng Idris sẽ coi một số là Integer theo mặc định, trừ khi có ngữ cảnh nào đó, và cả hai toán hạng phải cùng kiểu. Do đó, trong biểu thức thứ hai của hai biểu thức trước đó, hằng số 6.0 chỉ có thể là một Double, vì vậy toàn bộ biểu thức là một Double, và 3 và 12 cũng được coi là Doubles.

REPL results

Kết quả gần đây nhất tại REPL luôn có thể được truy xuất và sử dụng trong các phép tính tiếp theo bằng cách sử dụng giá trị đặc biệt it:

Idris> 6 + 3 * 12 42 : Integer Idris> it * 2 84 : Integer

Cũng có thể gán các biểu thức cho tên tại REPL bằng cách sử dụng lệnh :let:

Idris> :let x = 100 Idris> x 100 : Integer Idris> :let y = 200.0 Idris> y 200.0 : Double

Khi một biểu thức, chẳng hạn như 6 + 3 * 12, có thể thuộc một trong vài loại, bạn có thể làm cho loại đó rõ ràng bằng cách ghi chú theo cú pháp <loại><biểu thức>, để nói rằng loại đó là loại cần thiết của biểu thức:

Idris> 6 + 3 * 12 42 : Integer Idris> the Int (6 + 3 * 12) 42 : Int Idris> the Double (6 + 3 * 12) 42.0 : Double

“the” expressions

Cái này không phải là cú pháp tích hợp sẵn mà là một hàm thông thường trong Idris, được định nghĩa trong Prelude, tận dụng các kiểu dữ liệu đầu tiên.

2.1.2.
Type conversions using cast

Các toán tử số học hoạt động trên bất kỳ loại số nào, nhưng cả hai đầu vào và đầu ra phải có cùng một loại. Đôi khi, vì vậy, bạn sẽ cần chuyển đổi giữa các loại.

Giả sử bạn đã định nghĩa một số Nguyên và một số Double tại REPL:

Idris> :let integerval = 6 * 6 Idris> :let doubleval = 0.1 Idris> integerval 36 : Integer Idris> doubleval 0.1 : Double

Nếu bạn cố gắng thêm integerval và doubleval, Idris sẽ phàn nàn rằng chúng không cùng loại.

Idris> integerval + doubleval (input):1:8-9:When checking an application of function Prelude.Classes.+: Type mismatch between Double (Type of doubleval) and Integer (Expected type)

Để khắc phục điều này, bạn có thể sử dụng hàm cast, hàm này chuyển đổi đầu vào của nó sang kiểu cần thiết, miễn là việc chuyển đổi đó là hợp lệ. Ở đây, bạn có thể chuyển đổi Integer thành Double:

Idris> cast integerval + doubleval 36.1 : Double

Idris hỗ trợ việc chuyển đổi giữa tất cả các kiểu nguyên thủy, và có thể thêm các phép chuyển đổi tự định nghĩa, như bạn sẽ thấy trong chương 7. Lưu ý rằng một số phép chuyển đổi có thể mất thông tin, chẳng hạn như chuyển đổi từ Double sang Integer.

Specifying the target of a cast

Bạn cũng có thể sử dụng để chỉ rõ loại mà bạn muốn chuyển đổi sang, như trong các ví dụ sau:

Idris> the Integer (cast 9.9) 9 : Integer Idris> the Double (cast (4 + 4)) 8.0 : Double

2.1.3.
Characters and strings

Idris cũng cung cấp các ký tự và chuỗi Unicode dưới dạng kiểu nguyên thủy, cùng với một số hàm nguyên thủy hữu ích để thao tác với chúng.

Character literals (of type Char) are enclosed in single quotation marks, such as 'a'.
String literals (of type String) are enclosed in double quotation marks, such as "Hello world!"

Giống như nhiều ngôn ngữ khác, Idris hỗ trợ các ký tự đặc biệt trong các ký tự và chuỗi văn bản bằng cách sử dụng các chuỗi thoát, bắt đầu bằng dấu gạch chéo ngược. Ví dụ, một ký tự xuống dòng được chỉ định bằng cách sử dụng \n:

Idris> :t '\n' '\n' : Char Idris> :t "Hello world!\n" "Hello world!\n" : String

Đây là những chuỗi thoát phổ biến nhất:

\' for a literal single quote
\" for a literal double quote
\\ for a literal backslash
\n for a newline character
\t for a tab character

Prelude định nghĩa một số chức năng hữu ích để thao tác với Chuỗi. Bạn có thể thấy một số trong những chức năng này được sử dụng tại REPL:

Idris> length "Hello!" 6 : Nat Idris> reverse "drawer" "reward" : String Idris> substr 6 5 "Hello world" "world" : String Idris> "Hello" ++ " " ++ "World" "Hello World" : String

Dưới đây là một giải thích ngắn gọn về các chức năng này:

length—Gives the length of its argument as a Nat because a String can’t have a negative length
reverse—Returns a reversed version of its input
substr—Returns a substring of an input string, given a position to start at and the desired length of the substring
++—An operator that concatenates two Strings

Lưu ý cú pháp của các lệnh gọi hàm. Trong Idris, các hàm được tách biệt với các tham số bởi khoảng trắng. Nếu tham số là một biểu thức phức tạp, nó phải được đặt trong dấu ngoặc, như sau:

Idris> length ("Hello" ++ " " ++ "World") 11 : Nat

Function syntax

Gọi hàm bằng cách tách các đối số bằng dấu cách có thể trông lạ lùng lúc đầu. Tuy nhiên, có một lý do chính đáng cho điều đó, như bạn sẽ khám phá khi chúng ta xem xét các loại hàm ở phần sau của chương này. Tóm lại, điều này làm cho việc thao tác với các hàm trở nên linh hoạt hơn rất nhiều.

2.1.4.
Booleans

Idris cung cấp một loại Bool để biểu diễn giá trị chân lý. Một Bool có thể có giá trị True hoặc False. Các toán tử && và || lần lượt biểu diễn toán tử logic "và" và "hoặc":

Idris> True && False False : Bool Idris> True || False True : Bool

Các toán tử so sánh thông thường (<, <=, ==, /=, >, >=) có sẵn:

Idris> 3 > 2 True : Bool Idris> 100 == 99 False : Bool Idris> 100 /= 99 True : Bool

Inequality

Toán tử bất đẳng thức trong Idris là /=, theo cú pháp của Haskell, thay vì !=, theo cú pháp của các ngôn ngữ như C và Java.

Cũng có một cấu trúc if...then...else. Đây là một biểu thức, vì vậy nó luôn phải bao gồm cả nhánh then và nhánh else. Ví dụ, bạn có thể viết một biểu thức đánh giá thành một thông điệp khác nhau dưới dạng String, tùy thuộc vào độ dài của một từ:

Idris> :let word = "programming" Idris> if length word > 10 then "What a long word!" else "Short word" "What a long word!" : String

2.2. Functions: the building blocks of Idris programs

Bây giờ khi bạn đã thấy một số kiểu dữ liệu cơ bản và một cấu trúc điều khiển đơn giản, bạn có thể bắt đầu định nghĩa các hàm. Trong phần này, bạn sẽ viết một số hàm Idris sử dụng các kiểu dữ liệu cơ bản mà bạn đã thấy cho đến bây giờ, tải chúng vào hệ thống Idris và kiểm tra chúng tại REPL. Bạn cũng sẽ thấy cách lập trình hàm cho phép bạn viết các chương trình tổng quát hơn theo hai cách:

Using variables in function types, so that functions can be written to work with several different types
Using higher-order functions to capture common programming patterns

2.2.1.
Function types and definitions

Các loại hàm được cấu thành từ một hoặc nhiều loại đầu vào và một loại đầu ra. Ví dụ, một hàm nhận một Int làm đầu vào và trả về một Int khác sẽ được viết là Int -> Int. Danh sách dưới đây cho thấy một định nghĩa hàm đơn giản với kiểu này, hàm double.

Listing 2.2.
A function to double an `Int` (Double.idr)

Bạn có thể thử chức năng này bằng cách gõ nó vào một tệp, Double.idr; tải nó vào Idris REPL bằng cách gõ idris Double.idr tại dấu nhắc shell; và sau đó thử một số ví dụ tại REPL:

*Double> double 47 94 : Int *Double> double (double 15) 60 : Int

Hình 2.1 cho thấy các thành phần của định nghĩa hàm này. Tất cả các hàm trong Idris, như double, được giới thiệu với một khai báo kiểu và sau đó được định nghĩa bằng các phương trình với bên trái và bên phải.

Figure 2.1.
The components of a function definition

Một biểu thức được đánh giá bằng cách viết lại biểu thức theo những phương trình này cho đến khi không còn có thể viết lại được nữa. Do đó, các hàm định nghĩa các quy tắc mà theo đó các biểu thức có thể được viết lại. Ví dụ, hãy xem xét định nghĩa của hàm gấp đôi:

double x = x + x

Điều này có nghĩa là mỗi khi bộ đánh giá Idris gặp một biểu thức dưới dạng double x, với một số biểu thức đại diện cho x, nó nên được viết lại thành x + x.

Vậy, trong ví dụ double (double 15),

First, the inner double 15 is rewritten as 15 + 15.
15 + 15 is rewritten as 30.
double 30 is rewritten as 30 + 30.
30 + 30 is rewritten as 60.

Evaluation order

Bạn có thể đã nhận thấy rằng thay vì chọn đánh giá biểu thức trong cùng là double 15 trước, bạn có thể đã chọn biểu thức bên ngoài (double 15), điều này sẽ giảm xuống thành double 15 + double 15. Cả hai thứ tự đều khả thi, và mỗi cách đều dẫn đến cùng một kết quả. Theo mặc định, Idris sẽ đánh giá biểu thức ở bên trong cùng trước. Nói cách khác, nó sẽ đánh giá các đối số của hàm trước khi đánh giá các định nghĩa hàm.

Có những lợi ích và bất lợi cho cả hai lựa chọn, và kết quả là chủ đề này đã được bàn luận rất lâu! Bây giờ không phải là thời điểm để xem xét lại cuộc tranh luận này, nhưng nếu bạn quan tâm, bạn có thể tìm hiểu về đánh giá lười biếng. Idris hỗ trợ đánh giá lười biếng bằng cách sử dụng kiểu rõ ràng, như bạn sẽ thấy trong chương 11.

Tùy chọn, bạn có thể đặt tên rõ ràng trong các kiểu đầu vào của một hàm. Ví dụ, bạn có thể viết kiểu của hàm gấp đôi như sau:

double : (value : Int) -> Int

Điều này có ý nghĩa hoàn toàn giống với tuyên bố trước đó (double : Int -> Int). Có hai lý do tại sao bạn có thể làm cho tên của các tham số trở nên rõ ràng:

Naming the argument in the type can give the reader some information about the purpose of the argument.
Naming the argument means you can refer to it later.

Bạn sẽ thấy nhiều điều hơn về điều này trong chương 4 khi chúng ta bắt đầu khám phá các kiểu phụ thuộc một cách sâu sắc. Hiện tại, hãy nhớ ví dụ về các kiểu cấp một từ chương 1, nơi tôi đã đưa ra kiểu Idris sau cho getStringOrInt:

getStringOrInt : (x : Bool) -> StringOrInt x

Tham số đầu tiên, kiểu Bool, được đặt tên là x, và sau đó xuất hiện trong kiểu trả về.

Type declarations are required!

Các hàm trong Idris phải có khai báo kiểu rõ ràng, như double : Int -> Int ở đây. Một số ngôn ngữ hàm khác, đặc biệt là Haskell và ML, cho phép lập trình viên bỏ qua khai báo kiểu và để trình biên dịch suy luận kiểu. Tuy nhiên, trong một ngôn ngữ có kiểu đầu tiên, điều này thường là điều không thể. Trong bất kỳ trường hợp nào, việc bỏ qua khai báo kiểu trong phát triển dựa trên kiểu là điều không mong muốn. Triết lý của chúng tôi là sử dụng kiểu để giúp chúng tôi viết chương trình, thay vì sử dụng chương trình để giúp chúng tôi suy luận kiểu!

2.2.2.
Partially applying functions

Khi một hàm có nhiều hơn một tham số, bạn có thể tạo một phiên bản chuyên biệt của hàm bằng cách bỏ qua các tham số sau. Điều này được gọi là áp dụng một phần.

Ví dụ, giả sử bạn có một hàm cộng hai số nguyên, được định nghĩa như sau trong tệp Partial.idr:

add : Int -> Int -> Int add x y = x + y

Nếu bạn áp dụng hàm cho hai tham số, nó sẽ được đánh giá là một Int:

*Partial> add 2 3 5 : Int

Nếu ngược lại, bạn chỉ áp dụng hàm cho một đối số, bỏ qua đối số thứ hai, Idris sẽ trả về một hàm có kiểu Int -> Int:

*Partial> add 2 add 2 : Int -> Int

Bằng cách áp dụng hàm cộng chỉ cho một tham số, bạn đã tạo ra một hàm chuyên biệt mới, add 2, hàm này cộng 2 vào tham số của nó. Bạn có thể thấy điều này rõ ràng hơn bằng cách tạo một hàm mới với :let:

*Partial> :let addTwo = add 2 *Partial> :t addTwo addTwo : Int -> Int *Partial> addTwo 3 5 : Int

Cú pháp áp dụng hàm, áp dụng các hàm cho các đối số chỉ bằng cách tách hàm khỏi đối số bằng khoảng trắng, cung cấp một cú pháp đặc biệt ngắn gọn cho việc áp dụng một phần. Việc áp dụng một phần là rất phổ biến trong các chương trình Idris, và bạn sẽ thấy một số ví dụ về nó sắp tới, trong phần 2.2.5.

2.2.3.
Writing generic functions: variables in types

Cũng như các kiểu cụ thể, chẳng hạn như Int, String và Bool, các kiểu hàm có thể chứa biến. Biến trong một kiểu hàm có thể được khởi tạo với các giá trị khác nhau, giống như các biến trong chính các hàm.

Ví dụ, hãy xem xét hàm đồng nhất, hàm này trả về đầu vào của nó mà không thay đổi. Hàm đồng nhất trên kiểu số nguyên (Ints) được viết như sau:

identityInt : Int -> Int identityInt x = x

Tương tự, hàm đồng nhất trên chuỗi được viết như sau:

identityString : String -> String identityString x = x

Và đây là hàm đồng nhất trên các giá trị Boolean:

identityBool : Bool -> Bool identityBool x = x

Bạn có thể đã nhận thấy một mẫu ở đây. Trong mỗi trường hợp, định nghĩa giống nhau! Bạn không cần biết gì về x vì bạn trả về nó không thay đổi trong mỗi trường hợp. Vì vậy, thay vì viết một hàm đồng nhất cho mỗi loại riêng biệt, bạn có thể viết một hàm đồng nhất duy nhất sử dụng một biến, ty, ở cấp độ kiểu, thay cho một kiểu cụ thể:

identity : ty -> ty identity x = x

The id function

Trên thực tế, có một hàm đồng nhất trong Prelude được gọi là id, được định nghĩa theo cách giống hệt như hàm identity ở đây.

Biến ty trong kiểu danh tính là một biến, đại diện cho bất kỳ kiểu nào. Do đó, danh tính có thể được gọi với bất kỳ kiểu đầu vào nào và sẽ trả về đầu ra có cùng kiểu với đầu vào.

Variable names in types

Bất kỳ tên nào xuất hiện trong một khai báo kiểu, bắt đầu bằng chữ cái thường và không được định nghĩa rõ ràng sẽ được giả định là một biến. Lưu ý rằng tôi cẩn thận gọi những thứ này là biến, thay vì biến kiểu. Điều này là vì, với các loại phụ thuộc, các biến trong các kiểu không nhất thiết chỉ đứng cho các kiểu, như bạn sẽ thấy trong chương 3.

Bạn đã thấy một dạng của hàm đồng nhất khi làm việc với các kiểu số: đó là một hàm đồng nhất. Nó được định nghĩa trong Prelude như sau:

the : (ty : Type) -> ty -> ty the ty x = x

Nó nhận một loại rõ ràng làm đối số đầu tiên, được đặt tên rõ ràng là ty. Loại của đối số thứ hai được xác định bởi giá trị đầu vào của đối số đầu tiên. Đây là một ví dụ đơn giản về các loại phụ thuộc đang hoạt động, ở chỗ giá trị của một đối số trước đó xác định loại của một đối số sau đó. Bạn có thể thấy điều này một cách rõ ràng tại REPL, bằng cách áp dụng một phần chỉ cho một đối số.

Idris> :t the Int the Int : Int -> Int Idris> :t the String the String : String -> String Idris> :t the Bool the Bool : Bool -> Bool

2.2.4.
Writing generic functions with constrained types

Hàm đầu tiên bạn thấy trong phần 2.2.1, double, nhân đôi giá trị Int được cung cấp làm đầu vào:

double : Int -> Int double x = x + x

Nhưng còn các kiểu số khác thì sao? Ví dụ, bạn cũng có thể viết một hàm để gấp đôi một Nat hoặc một Integer:

doubleNat : Nat -> Nat doubleNat x = x + x doubleInteger : Integer -> Integer doubleInteger x = x + x

Như với danh tính, có lẽ bạn đã bắt đầu nhận thấy một mẫu ở đây, vì vậy hãy xem điều gì xảy ra nếu chúng ta cố gắng thay thế các loại đầu vào và đầu ra bằng một biến. Đưa đoạn sau vào một tệp có tên Generic.idr và tải nó vào Idris:

double : ty -> ty double x = x + x

Bạn sẽ thấy rằng Idris từ chối định nghĩa này, với thông báo lỗi như sau:

Generic.idr:2:8: When checking right hand side of double with expected type ty ty is not a numeric type

Vấn đề là, khác với identity, double cần biết một số thông tin về đầu vào x của nó, cụ thể là nó phải là kiểu số. Bạn chỉ có thể sử dụng các toán tử số học trên các kiểu số, vì vậy bạn cần giới hạn ty để nó chỉ đại diện cho các kiểu số. Danh sách sau đây cho thấy cách bạn có thể làm điều này.

Listing 2.3.
A generic type, constrained to numeric types (Generic.idr)

Loại Num ty => ty -> ty có thể được hiểu là “Một hàm nhận đầu vào với kiểu ty và trả ra kiểu ty với điều kiện rằng ty là một kiểu số.”

Type constraints

Các ràng buộc về kiểu tổng quát có thể được định nghĩa bởi người dùng bằng cách sử dụng giao diện, điều này sẽ được chúng tôi đề cập sâu hơn trong chương 7. Ở đây, Num là một giao diện được cung cấp bởi Idris. Giao diện có thể được cung cấp các triển khai cho các kiểu cụ thể, và giao diện Num có các triển khai cho các kiểu số.

Có lẽ đáng ngạc nhiên, các phép toán số học và so sánh không phải là các phép toán nguyên thủy trong Idris, mà thực ra là các hàm với kiểu dữ liệu tổng quát có ràng buộc. Các toán tử ở giữa như +, ==, và <= thực sự là các hàm có hai đối số, như bạn có thể thấy khi kiểm tra kiểu của chúng tại REPL:

Idris> :t (+) (+) : Num ty => ty -> ty -> ty Idris> :t (==) (==) : Eq ty => ty -> ty -> Bool Idris> :t (<=) (<=) : Ord ty => ty -> ty -> Bool

Cũng như Num cho các kiểu số, ở đây bạn có thể thấy hai ràng buộc khác được cung cấp bởi Idris:

Eq states that the type must support the equality and inequality operators, == and /=.
Ord states that the type must support the comparison operators <, <=, >, and >=.

Infix operators and operator sections

Các toán tử infix trong Idris không phải là phần nguyên thủy của cú pháp, mà được định nghĩa bởi các hàm. Việc đặt các toán tử trong dấu ngoặc, như với (+), (==), và (<=) trong ví dụ REPL, có nghĩa là chúng sẽ được xử lý như cú pháp hàm thông thường. Ví dụ, bạn có thể áp dụng (+) cho một đối số:

Idris> :t (+) 2 (+) 2 : Integer -> Integer

Các toán tử in-fix cũng có thể được áp dụng một phần bằng cách sử dụng các đoạn toán tử:

(< 3) gives a function that returns whether its input is less than 3.
(3 <) gives a function that returns whether 3 is less than its input.

Một toán tử trong dấu ngoặc với chỉ một đối số do đó được coi là một hàm mong đợi đối số còn thiếu khác.

2.2.5.
Higher-order function types

Không có giới hạn nào về việc loại đối số hoặc kiểu trả về của một hàm có thể là gì. Bạn đã thấy cách mà các hàm có nhiều đối số thực ra là các hàm trả về một cái gì đó với kiểu hàm. Tương tự, các hàm có thể nhận các hàm làm đối số. Các hàm như vậy được gọi là hàm bậc cao.

Các hàm bậc cao có thể được sử dụng để tạo ra các trừu tượng cho các mẫu lập trình lặp lại. Ví dụ, giả sử bạn đã định nghĩa một hàm quadruple mà nhân bốn giá trị đầu vào cho bất kỳ số nào, sử dụng hàm double:

quadruple : Num a => a -> a quadruple x = double (double x)

Hoặc nói bạn có một kiểu Shape đại diện cho bất kỳ hình dạng hình học nào, và một hàm rotate : Shape -> Shape được thực hiện thao tác xoay một hình qua 90 độ. Bạn có thể định nghĩa một hàm turn_around để xoay một hình qua 180 độ như sau:

turn_around : Shape -> Shape turn_around x = rotate (rotate x)

Mỗi chức năng trong số này có cùng một mẫu, nhưng chúng hoạt động trên các loại đầu vào khác nhau. Bạn có thể nắm bắt mẫu này bằng cách sử dụng một hàm bậc cao để áp dụng một hàm cho một đối số hai lần. Danh sách tiếp theo cung cấp định nghĩa của một hàm twice, cùng với các định nghĩa mới của hàm quadruple và rotate.

Listing 2.4.
Defining `quadruple` and `rotate` using a higher-order function (HOF.idr)

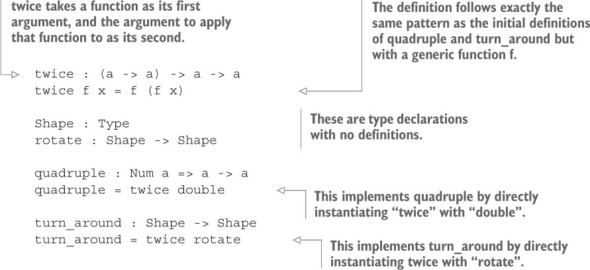
Trong chương 1, tôi đã giới thiệu khái niệm "lỗ", là những định nghĩa hàm chưa hoàn chỉnh. Các khai báo kiểu không có định nghĩa trong danh sách 2.4, Hình dạng và xoay, được coi là lỗ. Chúng cho phép bạn thử một ý tưởng (chẳng hạn như cách triển khai turn_around theo cách xoay) mà không cần định nghĩa đầy đủ các kiểu và hàm.

Partial application in definitions

Trong danh sách 2.4, quadruple và turn_around có kiểu hàm, Num a => a -> a và Shape -> Shape, tương ứng, nhưng trong định nghĩa của chúng, cả hai đều không có đối số.

Yêu cầu duy nhất khi kiểm tra một định nghĩa là cả hai bên của định nghĩa phải có cùng loại. Bạn có thể kiểm tra rằng điều này đúng bằng cách xem xét các loại của hai bên trái và phải của định nghĩa tại REPL. Bạn có định nghĩa sau đây:

turn_around = twice rotate

Bằng cách kiểm tra các kiểu tại REPL, bạn có thể thấy rằng cả turn_around và twice rotate đều có cùng kiểu:

Idris> :t turn_around turn_around : Shape -> Shape Idris> :t twice rotate twice rotate : Shape -> Shape

Các định nghĩa của quadruple và turn_around đều sử dụng ứng dụng một phần, như đã mô tả trong phần 2.2.2.

Một ứng dụng phổ biến khác của việc áp dụng một phần là trong việc xây dựng các đối số cho các hàm bậc cao. Hãy xem xét ví dụ này, sử dụng HOF.idr và thêm định nghĩa của hàm add từ phần 2.2.2:

*HOF> twice (add 5) 10 20 : Int

Điều này sử dụng một ứng dụng từng phần của hàm cộng để cộng 5 vào một số nguyên, hai lần. Bởi vì hàm twice yêu cầu một hàm nhận một tham số, trong khi hàm add nhận hai tham số, bạn có thể áp dụng hàm add cho một tham số để nó có thể sử dụng trong một ứng dụng của hàm twice.

Bạn cũng có thể sử dụng phần toán tử, như đã mô tả ở cuối phần 2.2.4:

*HOF> twice (5 +) 10 20 : Integer

Lưu ý rằng, trong trường hợp không có thông tin kiểu nào khác, Idris đã mặc định sang Integer, như được mô tả trong phần 2.1.1.

2.2.6.
Anonymous functions

Khi sử dụng các hàm bậc cao, thường thì việc truyền một hàm vô danh như một đối số là rất hữu ích. Một hàm vô danh thường là một hàm nhỏ mà bạn chỉ mong muốn sử dụng một lần, vì vậy không cần phải tạo một định nghĩa ở cấp độ cao hơn cho nó.

Ví dụ, bạn có thể truyền một hàm ẩn danh mà bình phương đầu vào của nó cho hàm twice:

*HOF> twice (\x => x * x) 2 16 : Integer

Các hàm ẩn danh được giới thiệu với một dấu gạch chéo ngược \ theo sau là danh sách các tham số. Nếu bạn kiểm tra loại của hàm ẩn danh trước đó, bạn sẽ thấy rằng nó có loại hàm.

*HOF> :t \x => x * x \x => x * x : Integer -> Integer

Hàm vô danh có thể nhận nhiều tham số, và các tham số có thể được chỉ định kiểu một cách tùy chọn.

*HOF> :t \x : Int, y : Int => x + y \x, y => x + y : Int -> Int -> Int

Lưu ý rằng đầu ra không hiển thị các loại một cách rõ ràng.

2.2.7.
Local definitions: let and where

Khi các hàm trở nên lớn hơn, thường là một ý tưởng tốt để chia chúng thành các định nghĩa nhỏ hơn. Idris cung cấp hai cấu trúc để định nghĩa biến và hàm cục bộ: let và where.

Hình 2.2 minh họa cú pháp cho các liên kết let, định nghĩa các biến cục bộ.

Nếu bạn đánh giá biểu thức này tại REPL, bạn sẽ thấy điều sau:

Idris> let x = 50 in x + x 100 : Integer

Figure 2.2.
A local variable definition: in the expression after the `in` keyword, `x` has the value `50`.

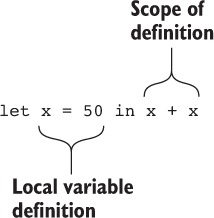
Danh sách tiếp theo hiển thị một ví dụ lớn hơn về let trong hành động. Nó định nghĩa một hàm, longer, nhận hai chuỗi và trả về độ dài của chuỗi lâu hơn. Nó sử dụng let để ghi lại độ dài của mỗi đầu vào.

Listing 2.5.
Local variables with `let` (Let_Where.idr)

Multiple lets

Có thể có nhiều định nghĩa trong một khối let. Trong danh sách 2.5, chẳng hạn, có hai biến cục bộ được định nghĩa trong khối let.

Trong khi các khối let chứa các định nghĩa biến cục bộ, các khối chứa các định nghĩa hàm cục bộ. Danh sách 2.6 cho thấy điều này đang hoạt động như thế nào. Nó định nghĩa một hàm để tính độ dài của cạnh huyền của một tam giác, sử dụng Định lý Pythagore và một hàm bình phương cục bộ.

Listing 2.6.
Local function definitions with `where` (Let_Where.idr)

Nói chung, let hữu ích cho việc chia nhỏ một biểu thức phức tạp thành các biểu thức con nhỏ hơn, trong khi where hữu ích cho việc định nghĩa các hàm phức tạp hơn chỉ có ý nghĩa trong ngữ cảnh cục bộ.

2.3. Composite types

Các kiểu hợp thành được tạo thành từ các kiểu khác. Trong phần này, chúng ta sẽ xem xét hai trong số các kiểu hợp thành phổ biến nhất được cung cấp bởi Idris: bộ và danh sách.

2.3.1.
Tuples

Một tuple là một tập hợp có kích thước cố định, trong đó mỗi giá trị trong tập hợp có thể có kiểu khác nhau. Ví dụ, một cặp bao gồm một số nguyên và một chuỗi có thể được viết như sau:

Idris> (94, "Pages") (94, "Pages") : (Integer, String)

Các tuple được viết dưới dạng danh sách các giá trị được phân cách bằng dấu phẩy và đặt trong dấu ngoặc. Lưu ý rằng kiểu của cặp (94, "Pages") là (Số nguyên, Chuỗi). Các kiểu tuple được viết bằng cú pháp giống như các giá trị tuple.

Các hàm fst và snd lần lượt trích xuất phần tử đầu tiên và thứ hai từ một cặp:

Idris> :let mypair = (94, "Pages") Idris> fst mypair 94 : Integer Idris> snd mypair "Pages" : String

Cả fst và snd đều có kiểu tổng quát, vì cặp có thể chứa bất kỳ kiểu nào. Bạn có thể kiểm tra kiểu của từng cái tại REPL:

Idris> :t fst fst : (a, b) -> a Idris> :t snd snd : (a, b) -> b

Bạn có thể đọc kiểu của fst, ví dụ, là “Cho một cặp a và b, trả về giá trị có kiểu a.” Trong những kiểu này, bạn biết rằng cả a và b đều là biến vì chúng bắt đầu bằng những chữ cái thường.

Hợp tuples có thể có bất kỳ số lượng thành phần nào, bao gồm cả số không.

Idris> ('x', 8, String) ('x', 8, String) : (Char, Integer, Type) Idris> () () : ()

Tuple rỗng, (), thường được gọi là “đơn vị” và kiểu của nó được gọi là “kiểu đơn vị.” Lưu ý rằng cú pháp này có thể bị quá tải, và Idris sẽ quyết định rằng () có nghĩa là đơn vị hay kiểu đơn vị từ ngữ cảnh.

Colors in the REPL

Bạn có thể đã nhận thấy rằng một số giá trị và kiểu trong REPL được tô màu khác nhau, đặc biệt khi đánh giá tuple rỗng (). Đây là đánh dấu ngữ nghĩa, và nó chỉ ra xem một biểu thức con là kiểu, giá trị, hàm hay biến. Theo mặc định, REPL hiển thị mỗi loại như sau:

Types are blue.
Values (more precisely, data constructors, as I’ll explain in chapter 3) are red.
Functions are green.
Variables are magenta.

Nếu những màu sắc này không phù hợp với sở thích của bạn hoặc khó phân biệt (ví dụ, nếu bạn bị mù màu), bạn có thể thay đổi cài đặt bằng lệnh :colour.

Các tuple cũng có thể được lồng ghép một cách tùy ý sâu.

Idris> (('x', 8), (String, 'y', 100), "Hello") (('x', 8), (String, 'y', 100), "Hello") : ((Char, Integer), (Type, Char, Integer), String)

Tuples and pairs

Bên trong, tất cả các tuple khác ngoài tuple rỗng được lưu trữ dưới dạng cặp lồng nhau. Điều này có nghĩa là nếu bạn viết (1, 2, 3, 4), Idris sẽ xử lý điều này theo cách tương tự như (1, (2, (3, 4))). REPL sẽ luôn hiển thị một tuple ở dạng không lồng nhau.

Idris> (1, (2, (3, 4))) (1, 2, 3, 4) : (Integer, Integer, Integer, Integer)

2.3.2.
Lists

Danh sách, giống như tuple, là các tập hợp giá trị. Khác với tuple, danh sách có thể có kích thước bất kỳ, nhưng mọi phần tử phải có cùng một kiểu. Danh sách được viết dưới dạng các giá trị phân tách bằng dấu phẩy trong ngoặc vuông, như sau.

Idris> [1, 2, 3, 4] [1, 2, 3, 4] : List Integer Idris> ["One", "Two", "Three", "Four"] ["One", "Two", "Three", "Four"] : List String

Loại của mỗi biểu thức này, Danh sách Số nguyên và Danh sách Chuỗi, chỉ ra loại phần tử mà Idris đã suy ra cho danh sách. Trong phát triển dựa trên kiểu, chúng ta thường cung cấp các kiểu trước, sau đó viết một giá trị hoặc hàm tương ứng thỏa mãn kiểu này. Tại REPL, sẽ rất bất tiện nếu làm điều này cho mỗi giá trị, vì vậy Idris sẽ cố gắng suy ra một kiểu cho giá trị đã cho. Thật không may, điều này không phải lúc nào cũng khả thi. Ví dụ, nếu bạn cung cấp cho nó một danh sách rỗng, Idris không biết loại phần tử nên là gì.

Idris> [] (input):Can't infer argument elem to []

Thông điệp lỗi này có nghĩa là Idris không thể xác định kiểu phần tử (mà được đặt tên là elem) cho danh sách rỗng []. Vấn đề này có thể được giải quyết trong trường hợp này bằng cách cung cấp một kiểu rõ ràng, sử dụng:

Idris> the (List Int) [] [] : List Int

Giống như chuỗi, danh sách có thể được nối với toán tử ++, với điều kiện rằng cả hai toán hạng đều có cùng loại phần tử.

Idris> [1, 2, 3] ++ [4, 5, 6, 7] [1, 2, 3, 4, 5, 6, 7] : List Integer

Bạn có thể thêm một phần tử vào đầu danh sách bằng cách sử dụng toán tử :: (đọc là “cons”):

Idris> 1 :: [2, 3, 4] [1, 2, 3, 4] : List Integer Idris> 1 :: 2 :: 3 :: 4 :: [] [1, 2, 3, 4] : List Integer

Syntactic sugar for lists

Toán tử :: là toán tử nguyên thuỷ để xây dựng các danh sách từ một phần tử đầu và một đuôi, và Nil là tên nguyên thuỷ cho danh sách rỗng. Do đó, một danh sách có thể ở một trong hai hình thức chuẩn sau:

Nil, the empty list
x :: xs, where x is an element, and xs is another list

Bởi vì điều này có thể trở nên khá dài dòng, Idris cung cấp cú pháp dễ chịu cho danh sách. Các hằng số danh sách bao gồm các phần tử ngăn cách bằng dấu phẩy bên trong dấu ngoặc vuông được biến đổi thành các dạng nguyên thủy này. Ví dụ, [] được biến đổi trực tiếp thành Nil, và [1, 2, 3] được biến đổi thành 1 :: (2 :: (3 :: Nil)).

Cũng có một ký hiệu ngắn gọn hơn cho các khoảng số. Dưới đây là một vài ví dụ:

[1..5] expands to the list [1, 2, 3, 4, 5].
[1,3..9] expands to the list [1, 3, 5, 7, 9].
[5,4..1] expands to the list [5, 4, 3, 2, 1].

Nói chung, [n..m] cho một danh sách tăng dần các số giữa n và m, và [n,m..p] cho một danh sách các số giữa n và p với bước nhảy được xác định bởi sự chênh lệch giữa n và m.

2.3.3.
Functions with lists

Chúng ta sẽ thảo luận về danh sách một cách sâu sắc hơn trong chương tiếp theo, bao gồm cách định nghĩa các hàm trên danh sách, nhưng có một số hàm hữu ích đã được định nghĩa trong Prelude. Hãy cùng xem xét một số hàm này.

Hàm `function`, có kiểu String -> List String, chuyển một chuỗi thành danh sách các thành phần được phân tách bằng khoảng trắng của chuỗi đó.

Sure, please provide the text you want to be translated into Vietnamese.
The words name comes from a similar function in the Haskell libraries. Many Idris function names follow Haskell terminology.

Idris> words "'Twas brillig, and the slithy toves" ["'Twas", "brillig,", "and", "the", "slithy", "toves"] : List String

Hàm unwords, có kiểu List String -> String, thực hiện ngược lại, chuyển đổi một danh sách các từ thành một chuỗi mà các từ được ngăn cách bằng một khoảng trống:

Idris> unwords ["One", "two", "three", "four!"] "One two three four!" : String

Bạn đã thấy một hàm độ dài để tính độ dài của chuỗi. Còn một hàm độ dài quá tải, kiểu List a -> Nat, cho biết độ dài của một danh sách:

Idris> length ["One", "two", "three", "four!"] 4 : Nat

Bạn có thể sử dụng độ dài và từ để viết một hàm đếm số từ cho chuỗi:

wordCount : String -> Nat wordCount str = length (words str)

Hàm map là một hàm bậc cao áp dụng một hàm cho mọi phần tử trong một danh sách. Nó có kiểu (a -> b) -> List a -> List b. Ví dụ này tìm độ dài của từng từ trong một danh sách:

Idris> map length (words "How long are these words?") [3, 4, 3, 5, 6] : List Nat

Bạn có thể sử dụng map và length để viết một hàm lấy độ dài của từng phần tử trong danh sách chuỗi.

allLengths : List String -> List Nat allLengths strs = map length strs

Type of map

Nếu bạn kiểm tra loại bản đồ tại REPL, bạn sẽ thấy điều gì đó hơi khác biệt:

Idris> :t map map : Functor f => (a -> b) -> f a -> f b

Lý do cho điều này là map có thể hoạt động trên nhiều cấu trúc khác nhau, không chỉ danh sách, vì vậy nó có một kiểu tổng quát hạn chế. Bạn sẽ tìm hiểu về Functor trong chương 7, nhưng trong thời điểm này, bạn có thể hiểu f như là List trong kiểu này.

Hàm lọc (filter) là một hàm bậc cao khác, dùng để lọc một danh sách theo một hàm Boolean. Nó có kiểu (a -> Bool) -> List a -> List a và trả về một danh sách mới chứa mọi phần tử trong danh sách đầu vào mà hàm trả về True. Ví dụ, đây là cách bạn tìm tất cả các số lớn hơn 10 trong một danh sách:

Idris> filter (> 10) [1,11,2,12,3,13,4,14] [11, 12, 13, 14] : List Integer

Overloading functions

Bạn đã thấy hàm length trên cả chuỗi và danh sách. Điều này hoạt động vì Idris cho phép các tên hàm được nạp chồng để hoạt động trên nhiều loại. Bạn có thể thấy điều gì đang xảy ra bằng cách kiểm tra kiểu của length tại REPL:

*lists> :t length Prelude.List.length : List a -> Nat Prelude.Strings.length : String -> Nat

Trên thực tế, có hai hàm gọi là length. Các tiền tố Prelude.List và Prelude.Strings là không gian tên mà các hàm này được định nghĩa. Idris xác định hàm length nào cần thiết từ ngữ cảnh mà nó được sử dụng.

Hàm sum, có kiểu Num a => List a -> a, tính tổng của một danh sách số.

Idris> sum [1..100] 5050 : Integer

Loại tổng cho biết mọi phần tử trong danh sách đầu vào phải có cùng một loại, a, và loại đó được giới hạn bởi Num.

Bạn bây giờ đã biết đủ để có thể định nghĩa một hàm có tên là average tính toán độ dài trung bình của các từ trong một chuỗi. Hàm này được định nghĩa trong danh sách tiếp theo, hiển thị tệp Idris hoàn chỉnh Average.idr.

Listing 2.7.
Calculating the average word length in a string (Average.idr)

Danh sách 2.7 cũng giới thiệu từ khóa mô-đun và xuất khẩu. Một khai báo mô-đun có thể được đặt tùy chọn ở đầu một tệp. Điều này khai báo một không gian tên trong đó mọi hàm được định nghĩa. Thông thường, tên mô-đun giống với tên tệp (không có phần mở rộng .idr). Từ khóa xuất khẩu cho phép hàm trung bình được sử dụng bởi các mô-đun khác nhập khẩu Average.idr.

Như thường lệ, bạn có thể thử điều này tại REPL bằng cách tải Average.idr vào Idris, và đánh giá như sau:

*Average> average "How long are these words?" 4.2 : Double

Modules and namespaces

Bằng cách thêm một khai báo mô-đun vào đầu file Average.idr, bạn khai báo một không gian tên cho các định nghĩa trong mô-đun. Ở đây, điều này có nghĩa là tên đầy đủ của hàm trung bình là Average.average. Một khai báo mô-đun phải là điều đầu tiên trong file. Nếu không có khai báo nào, Idris sẽ gọi mô-đun là Main.

Các mô-đun cho phép bạn chia nhỏ các chương trình Idris lớn một cách hợp lý thành nhiều tệp nguồn, mỗi tệp có mục đích riêng. Chúng có thể được nhập vào bằng câu lệnh import. Ví dụ:

import Average will import the definitions from Average.idr, provided that Average.idr is either in the current directory or in some other path that Idris can find.
import Utils.Average will import the definitions from Average.idr in a subdirectory called Utils, provided that the file and subdirectory exist.

Các mô-đun có thể được kết hợp thành các gói và phân phối riêng biệt. Về mặt kỹ thuật, Prelude được định nghĩa trong một mô-đun gọi là Prelude, mô-đun này tự nhập nhiều mô-đun khác, và là một phần của một gói gọi là prelude. Bạn có thể tìm hiểu thêm về các gói và cách tạo gói của riêng mình từ tài liệu gói của Idris tại http://idris-lang.org/documentation/packages.

2.4. A complete Idris program

Cho đến nay, bạn đã thấy cách viết hàm với các kiểu dữ liệu tích hợp và một số phép toán cơ bản trên các kiểu đó. Hàm là những khối xây dựng cơ bản của chương trình Idris, vì vậy bây giờ khi bạn đã viết một số hàm đơn giản, đã đến lúc xem cách kết hợp chúng để xây dựng một chương trình hoàn chỉnh.

2.4.1.
Whitespace significance: the layout rule

Khoảng trắng, đặc biệt là thụt lề, là rất quan trọng trong các chương trình Idris. Khác với một số ngôn ngữ khác, không có dấu ngoặc hoặc dấu chấm phẩy để chỉ ra nơi bắt đầu và kết thúc của các biểu thức, khai báo kiểu và định nghĩa. Thay vào đó, trong bất kỳ danh sách định nghĩa và khai báo nào, tất cả phải bắt đầu ở cùng một cột chính xác. Danh sách 2.8 minh họa nơi các định nghĩa và khai báo bắt đầu và kết thúc theo quy tắc này trong một tệp chứa định nghĩa trước đó của hàm trung bình.

Spaces and tabs

Một sự phức tạp với ý nghĩa khoảng trắng là kích thước tab có thể được cài đặt khác nhau trong các trình soạn thảo khác nhau, và Idris mong đợi rằng các tab và khoảng trắng được sử dụng một cách nhất quán. Để tránh bất kỳ sự nhầm lẫn nào với kích thước tab, tôi rất khuyến nghị bạn nên cài đặt trình soạn thảo của mình để thay thế tab bằng khoảng trắng!

Listing 2.8.
The layout rule applied to `average` (Average.idr)

Ví dụ, nếu allLengths được thụt vào thêm một khoảng trắng, như trong danh sách 2.9, nó sẽ được coi là một phần tiếp theo của định nghĩa trước đó về wordCount, và do đó sẽ không hợp lệ.

Listing 2.9.
The layout rule, applied incorrectly

2.4.2.
Documentation comments

Như với bất kỳ ngôn ngữ nào khác, việc bình luận các định nghĩa là một thói quen tốt để giúp người đọc mã hiểu mục đích của các hàm và tài liệu cách chúng hoạt động. Idris cung cấp ba loại chú thích:

Single-line comments, introduced with -- (two minus signs). These comments continue to the end of the line.
Multiline nested comments, introduced with {- and ending with -}.
Documentation comments, which are used to provide documentation for functions and types at the REPL.

Hai loại chú thích đầu tiên là thông thường, và chỉ đơn giản khiến phần được chú thích bị bỏ qua (cú pháp giống hệt cú pháp của các chú thích trong Haskell).

Tài liệu nhận xét, mặt khác, làm cho tài liệu có sẵn tại REPL, có thể truy cập bằng lệnh :doc. Bạn có thể xem tài liệu cho một số loại và chức năng mà chúng ta đã gặp cho đến nay. Ví dụ, :doc fst tạo ra đầu ra sau:

Idris> :doc fst Prelude.Basics.fst : (a, b) -> a Return the first element of a pair. The function is Total

Đầu ra này bao gồm tên đầy đủ của hàm fst, cho thấy nó được định nghĩa trong module Prelude.Basics, và chỉ ra rằng hàm này là tổng quát, có nghĩa là nó được đảm bảo sẽ sản xuất một kết quả cho tất cả các đầu vào.

Bạn cũng có thể tìm tài liệu cho các kiểu. Ví dụ, :doc List sẽ cho ra đầu ra sau:

Idris> :doc List Data type Prelude.List.List : Type -> Type Generic lists Constructors: Nil : List elem The empty list (::) : elem -> List elem -> List elem A non-empty list, consisting of a head element and the rest of the list. infixr 7

Một lần nữa, điều này cung cấp tên đầy đủ của kiểu Prelude.List.List. Nó cũng cung cấp các bộ tạo, là những cách nguyên thủy để xây dựng danh sách. Cuối cùng, đối với toán tử ::, nó cung cấp độ kết hợp, cho biết toán tử này có tính kết hợp phải (infixr) và có mức độ ưu tiên 7. Tôi sẽ mô tả mức độ ưu tiên và tính kết hợp của các toán tử chi tiết hơn trong chương 3.

Các chú thích tài liệu, tạo ra tài liệu này, được bắt đầu bằng ba dấu gạch đứng, |||. Ví dụ, bạn có thể tài liệu hóa biến trung bình như sau:

||| Calculate the average length of words in a string. average : String -> Double

Sau đó, :doc average sẽ tạo ra đầu ra như sau:

*Average> :doc average Average.average : (str : String) -> Double Calculate the average length of words in a string. The function is Total

Bạn có thể tham khảo lập luận trung bình bằng cách đặt tên cho nó là str, và đề cập đến tên đó trong chú thích với @str:

||| Calculate the average length of words in a string. ||| @str a string containing words separated by whitespace. average : (str : String) -> Double average str = let numWords = wordCount str totalLength = sum (allLengths (words str)) in cast totalLength / cast numWords

Điều này làm cho sản xuất trung bình của :doc có đầu ra thông tin chính xác hơn.

*Average> :doc average Main.average : (str : String) -> Double Calculate the average length of words in a string. Arguments: str : String -- a string containing words separated by whitespace. The function is Total

Totality checking

Lưu ý rằng: tài liệu trung bình báo cáo rằng trung bình là tổng. Idris kiểm tra từng định nghĩa về tính toàn vẹn. Kết quả của việc kiểm tra tính toàn vẹn có nhiều hệ quả thú vị trong phát triển dựa trên kiểu dữ liệu, mà chúng ta sẽ thảo luận trong suốt cuốn sách, đặc biệt là ở các chương 10 và 11.

2.4.3.
Interactive programs

Điểm nhập của một chương trình Idris đã biên dịch là hàm main, được định nghĩa trong module Main. Đó là hàm có tên hoàn chỉnh là Main.main. Nó phải có kiểu IO (), có nghĩa là nó trả về một hành động IO cung cấp một bộ tuple rỗng.

Bạn đã thấy chương trình "Xin chào, thế giới Idris!" rồi:

main : IO () main = putStrLn "Hello Idris World!"

Ở đây, putStrLn là một hàm có kiểu String -> IO () nhận một chuỗi làm đối số và trả về một hành động IO xuất chuỗi đó. Chúng ta sẽ thảo luận về các hành động IO một cách sâu sắc trong chương 5, nhưng ngay cả trước đó, bạn sẽ có thể viết các chương trình tương tác hoàn chỉnh bằng Idris sử dụng hàm repl (và một số biến thể của nó, như bạn sẽ thấy trong chương 4) được cung cấp bởi Prelude:

Idris> :doc repl Prelude.Interactive.repl : (prompt : String) -> A basic read-eval-print loop Arguments: prompt : String -- the prompt to show onInput : String -> String -- the function to run on reading input, returning a String to output

Điều này cho phép bạn viết các chương trình mà lặp đi lặp lại hiển thị một lời nhắc, đọc một số đầu vào và tạo ra một số đầu ra bằng cách chạy một hàm có kiểu String -> String trên nó. Ví dụ, danh sách tiếp theo là một chương trình mà lặp đi lặp lại đọc một chuỗi và sau đó in chuỗi đó theo chiều ngược lại.

Listing 2.10.
Reversing strings interactively (Reverse.idr)

module Main main : IO () main = repl "> " reverse

Bạn có thể biên dịch và chạy chương trình này tại REPL bằng lệnh :exec. Lưu ý rằng chương trình sẽ lặp vô hạn, nhưng bạn có thể thoát bằng cách ngắt chương trình bằng Ctrl-C:

*reverse> :exec > hello! !olleh> goodbye eybdoog>

Để kết thúc chương này, bạn sẽ viết một chương trình nhập mô-đun Average, đọc một chuỗi từ bảng điều khiển và hiển thị số chữ cái trung bình trong mỗi từ trong chuỗi. Một khó khăn là hàm average trả về một giá trị Double, nhưng repl yêu cầu một hàm loại String -> String, vì vậy bạn không thể sử dụng average trực tiếp. Nói chung, giá trị có thể được chuyển đổi thành String bằng cách sử dụng hàm show. Hãy cùng xem nó bằng cách sử dụng :doc:

Idris> :doc show Prelude.Show.show : Show ty => (x : ty) -> String Convert a value to its String representation.

Lưu ý rằng đây là một kiểu tổng quát bị ràng buộc, có nghĩa là kiểu ty phải hỗ trợ giao diện Show, điều này đúng với tất cả các kiểu trong Prelude.

Sử dụng điều này, bạn có thể viết một hàm showAverage sử dụng hàm average để lấy độ dài trung bình của từ và hiển thị nó trong một chuỗi được định dạng đẹp. Chương trình hoàn chỉnh được cung cấp trong danh sách dưới đây.

Listing 2.11.
Displaying average word lengths interactively (AveMain.idr)

Một lần nữa, bạn có thể sử dụng :exec để biên dịch và chạy điều này tại REPL, và sau đó thử một số đầu vào:

*AveMain> :exec Enter a string: The quick brown fox jumped over the lazy dog The average word length is: 4 Enter a string: The quick brown fox jumped over the lazy frog The average word length is: 4.11111 Enter a string:

Exercises

What are the types of the following values?
- (“A”, “B”, “C”)
- [“A”, “B”, “C”]
- (('A', “B”), 'C')
You can check your answers with :t at the REPL, but try to work them out yourself first.
Write a palindrome function, of type String -> Bool, that returns whether the input reads the same backwards as forwards. Hint: You may find the function reverse : String -> String useful. You can test your answer at the REPL as follows:
```
*ex_2> palindrome "racecar" True : Bool *ex_2> palindrome "race car" False : Bool
```
Modify the palindrome function so that it’s not case sensitive. Hint: You may find toLower : String -> String useful. You can test your answer at the REPL as follows:
```
*ex_2> palindrome "Racecar" True : Bool
```
Modify the palindrome function so that it only returns True for strings longer than 10 characters. You can test your answer at the REPL as follows:
```
*ex_2> palindrome "racecar" False : Bool *ex_2> palindrome "able was i ere i saw elba" True : Bool
```
Modify the palindrome function so that it only returns True for strings longer than some length given as an argument. Hint: Your new function should have type Nat -> String -> Bool. You can test your answer at the REPL as follows:
```
*ex_2> palindrome 10 "racecar" False : Bool *ex_2> palindrome 5 "racecar" True : Bool
```
Write a counts function of type String -> (Nat, Nat) that returns a pair of the number of words in the input and the number of characters in the input. You can test your answer at the REPL as follows:
```
*ex_2> counts "Hello, Idris world!" (3, 19) : (Nat, Nat)
```
Write a top_ten function of type Ord a => List a -> List a that returns the ten largest values in a list. You may find the following Prelude functions useful:
- take : Nat -> List a -> List a
- sort : Ord a => List a -> List a
Use :doc for further information about these functions if you need it. You can test your answer at the REPL as follows:
```
*ex_2> top_ten [1..100] [100, 99, 98, 97, 96, 95, 94, 93, 92, 91] : List Integer
```
Write an over_length function of type Nat -> List String -> Nat that returns the number of strings in the list longer than the given number of characters. You can test your answer at the REPL as follows:
```
*ex_2> over_length 3 ["One", "Two", "Three", "Four"] 2 : Nat
```
For each of palindrome and counts, write a complete program that prompts for an input, calls the function, and prints its output. You can test your answer using :exec at the REPL:
```
*ex_2_palindrome> :exec Enter a string: Able was I ere I saw Elba True Enter a string: Madam, I'm Adam False Enter a string:
```

2.5. Summary

The Prelude defines a number of basic types and functions and is imported automatically by all Idris programs.
Idris provides basic numeric types, Int, Integer, Nat, and Double, as well as a Boolean type, Bool, a character type, Char, and a string type, String.
Values can be converted between compatible types using the cast function, and can be given explicit types with the the function.
Tuples are fixed-size collections where each element can be a different type.
Lists are variable size collections where each element has the same type.
Function types have one or more input types and one output type.
Function types can be generic, meaning that they can contain variables. These variables can be constrained to allow a smaller set of types.
Higher-order functions are functions in which one of the arguments is itself a function.
Functions consist of a required type declaration and a definition. Function definitions are equations defining rewrite rules to be used during evaluation.
Whitespace is significant in Idris programs. Each definition in a block must begin in exactly the same column.
Function documentation can be accessed at the REPL with the :doc command.
Idris programs can be divided into separate source files called modules.
The entry point to an Idris program is the main function, which must have type IO (), and be defined in the module Main. Simple interactive programs can be written by applying the repl function from main.

Part 2.
Core Idris

Bây giờ bạn đã có một số kinh nghiệm viết chương trình bằng Idris, đã đến lúc bắt đầu khám phá phát triển dựa trên kiểu một cách sâu sắc. Trong phần này, bạn sẽ tìm hiểu về các tính năng cốt lõi của Idris và có được một số kinh nghiệm trong quá trình phát triển dựa trên kiểu. Thay vì chỉ cho bạn các chương trình hoàn chỉnh ngay từ đầu, tôi sẽ chỉ cho bạn cách xây dựng các chương trình một cách tương tác, thông qua quá trình xác định kiểu, định nghĩa, tinh chỉnh:

Type— Write a type for a function.
Define— Create an initial definition for the function, possibly containing holes.
Refine— Complete the definition by filling in holes, possibly modifying the type as your understanding of the problem develops.

Trong chương 3, bạn sẽ học những điều cơ bản về phát triển tương tác; sau đó, trong chương 4, bạn sẽ học cách định nghĩa các kiểu dữ liệu riêng của mình và xây dựng các chương trình lớn hơn xung quanh chúng. Chương 5 chỉ ra cách bạn có thể viết các chương trình tương tác với thế giới bên ngoài, sử dụng các kiểu để tách biệt việc đánh giá và thực thi. Các chương sau giới thiệu những khái niệm nâng cao hơn trong phát triển dựa trên kiểu, bao gồm tính toán cấp kiểu trong chương 6, làm việc với các kiểu tổng quát có ràng buộc trong chương 7, mô tả và chứng minh các thuộc tính của các chương trình trong các chương 8 và 9, và định nghĩa các cách duyệt thay thế các cấu trúc dữ liệu bằng cách sử dụng các chế độ xem trong chương 10.

Đến cuối phần 2, bạn sẽ đã tìm hiểu về tất cả các tính năng cốt lõi của Idris.

Chapter 3.
Interactive development with types

Chương này đề cập đến

Defining functions by pattern matching
Type-driven interactive editing in Atom
Adding precision to function types
Practical programming with vectors

Bạn đã thấy cách định nghĩa các hàm đơn giản và cách cấu trúc chúng thành các chương trình hoàn chỉnh. Trong chương này, chúng ta sẽ bắt đầu khám phá sâu hơn về phát triển dựa trên kiểu. Đầu tiên, chúng ta sẽ xem cách viết các hàm phức tạp hơn với các kiểu có sẵn từ Prelude, chẳng hạn như danh sách. Sau đó, chúng ta sẽ xem xét việc sử dụng hệ thống kiểu của Idris để cung cấp cho các hàm các kiểu chính xác hơn.

Trong phát triển dựa trên kiểu, chúng ta thực hiện quy trình "gõ, định nghĩa, tinh chỉnh." Bạn sẽ thấy quy trình này trong suốt chương này khi bạn đầu tiên viết các kiểu và, trong khả năng có thể, luôn có một định nghĩa đúng kiểu, mặc dù có thể chưa hoàn chỉnh, của một hàm và tinh chỉnh nó từng bước cho đến khi hoàn thành. Mỗi bước sẽ được mô tả rộng rãi là một trong ba cái sau:

Type— Either write a type to begin the process, or inspect the type of a hole to decide how to continue the process.
Define—
Create the structure of a function definition either by creating an outline of a definition or breaking it down into smaller components.
Refine— Improve an existing definition either by filling in a hole or making its type more precise.

Trong chương này, tôi sẽ giới thiệu việc phát triển tương tác trong trình soạn thảo văn bản Atom, hỗ trợ quá trình này. Atom cung cấp chế độ chỉnh sửa tương tác giao tiếp với hệ thống Idris đang chạy và sử dụng các kiểu để giúp chỉ đạo phát triển hàm. Atom cũng cung cấp một số tính năng chỉnh sửa cấu trúc và thông tin ngữ cảnh về các hàm còn thiếu, và khi các kiểu đủ chính xác, thậm chí hoàn thành một phần lớn của các hàm cho bạn. Do đó, tôi sẽ bắt đầu chương này bằng cách giới thiệu chế độ chỉnh sửa tương tác trong Atom.

Editor modes

Mặc dù chúng ta sẽ sử dụng Atom để chỉnh sửa các chương trình Idris, nhưng các tính năng tương tác mà chúng ta sẽ sử dụng được cung cấp bởi chính Idris. Việc tích hợp Atom hoạt động bằng cách giao tiếp với một tiến trình Idris chạy ở chế độ nền. Tiến trình này được chạy như một tiến trình con của trình chỉnh sửa, vì vậy nó độc lập với bất kỳ REPL nào bạn có thể đang chạy. Do đó, việc thêm hỗ trợ Idris vào các trình chỉnh sửa văn bản khác là khá đơn giản, và các chế độ chỉnh sửa tương tự hiện có cho Emacs và Vim. Trong cuốn sách này, chúng ta sẽ giữ nguyên việc sử dụng Atom để đảm bảo tính nhất quán, nhưng mỗi lệnh sẽ tương ứng với các lệnh tương tự trong các trình chỉnh sửa khác.

3.1. Interactive editing in Atom

Bạn đã thấy trong chương 1 rằng các chương trình Idris có thể chứa các lỗ hổng, đại diện cho các phần của định nghĩa hàm chưa được viết. Đây là một trong những cách mà chương trình có thể được phát triển một cách tương tác: bạn viết một định nghĩa chưa hoàn chỉnh chứa lỗ hổng, kiểm tra kiểu của các lỗ hổng để xem Idris mong đợi gì ở mỗi lỗ hổng, và sau đó tiếp tục điền vào các lỗ hổng bằng mã thêm. Có vài cách bổ sung mà Idris có thể giúp bạn bằng cách tích hợp các tính năng phát triển tương tác với trình soạn thảo văn bản:

Add definitions— Given a type declaration, Idris can add a skeleton definition of a function that satisfies that type.
Case analysis— Given a skeleton function definition with arguments, Idris can use the types of those arguments to help define the function by pattern matching.
Expression search— Given a hole with a precise enough type, Idris can try to find an expression that satisfies the hole’s type, refining the definition.

Trong phần này, chúng ta sẽ bắt đầu viết một số hàm Idris phức tạp hơn, sử dụng các tính năng chỉnh sửa tương tác để phát triển những hàm đó, từng bước một, theo cách hướng theo kiểu. Chúng ta sẽ sử dụng trình soạn thảo văn bản Atom, vì có một tiện ích mở rộng có sẵn để chỉnh sửa các chương trình Idris, có thể được cài đặt trực tiếp từ bản phân phối mặc định của Atom. Phần còn lại của chương này giả định rằng bạn đã khởi động và chạy chế độ Idris tương tác. Nếu không, hãy làm theo hướng dẫn trong phụ lục A để cài đặt Atom và chế độ Idris.

3.1.1.
Interactive command summary

Chỉnh sửa tương tác trong Atom liên quan đến một số lệnh bàn phím trong trình biên tập, được tóm tắt trong bảng 3.1.

Command mnemonics

Đối với mỗi lệnh, phím tắt trong Atom là nhấn Ctrl, Alt và chữ cái đầu tiên của lệnh.

Table 3.1.
Interactive editing commands in Atom

Phím tắt	Lệnh	Mô tả
Ctrl-Alt-A	Add definition	Adds a skeleton definition for the name under the cursor
Ctrl-Alt-C	Case split	Splits a definition into pattern-matching clauses for the name under the cursor
Ctrl-Alt-D	Documentation	Displays documentation for the name under the cursor
Ctrl-Alt-L	Lift hole	Lifts a hole to the top level as a new function declaration
Ctrl-Alt-M	Match	Replaces a hole with a case expression that matches on an intermediate result
Ctrl-Alt-R	Reload	Reloads and type-checks the current buffer
Ctrl-Alt-S	Search	Searches for an expression that satisfies the type of the hole name under the cursor
Ctrl-Alt-T	Type-check name	Displays the type of the name under the cursor

3.1.2.
Defining functions by pattern matching

Tất cả các định nghĩa hàm mà chúng ta đã xem cho đến nay đều liên quan đến một phương trình duy nhất để xác định hành vi của hàm đó. Ví dụ, trong chương trước, bạn đã viết một hàm để tính độ dài của từng từ trong một danh sách:

allLengths : List String -> List Nat allLengths strs = map length strs

Ở đây, bạn đã sử dụng các hàm được định nghĩa trong Prelude (map và length) để kiểm tra danh sách. Tuy nhiên, đến một lúc nào đó, bạn sẽ cần một cách trực tiếp hơn để kiểm tra các giá trị. Cuối cùng, các hàm như map và length cũng cần được định nghĩa bằng một cách nào đó!

Nói chung, bạn định nghĩa các hàm bằng cách khớp mẫu với các giá trị có thể của đầu vào cho một hàm. Ví dụ, bạn có thể định nghĩa một hàm để đảo ngược giá trị của một Bool như sau:

invert : Bool -> Bool invert False = True invert True = False

Các đầu vào có thể của loại Bool là True và False, do đó ở đây bạn thực hiện phép đảo bằng cách liệt kê các đầu vào có thể và đưa ra các đầu ra tương ứng. Các mẫu cũng có thể chứa các biến, như được minh họa bởi hàm sau, hàm này trả về "Trống" nếu nhận được một danh sách trống hoặc "Không trống" theo sau là giá trị của đuôi nếu nhận được một danh sách không trống:

describeList : List Int -> String describeList [] = "Empty" describeList (x :: xs) = "Non-empty, tail = " ++ show xs

Hình 3.1 minh họa cách các mẫu được so khớp trong describeList cho các đầu vào [1] (được coi là cú pháp ngắn gọn cho 1 :: []) và [2,3,4,5] (được coi là cú pháp ngắn gọn cho 2 :: 3 :: 4 :: 5 :: []).

Figure 3.1.
Matching the pattern `(x :: xs)` for inputs `[1]` and `[2,3,4,5]`

Naming conventions for lists

Thông thường, khi làm việc với danh sách và các cấu trúc giống danh sách, các lập trình viên Idris sử dụng một tên kết thúc bằng “s” (để gợi ý về số nhiều), và sau đó sử dụng hình thức số đơn để tham chiếu đến các phần tử riêng lẻ. Vì vậy, nếu bạn có một danh sách gọi là things, bạn có thể tham chiếu đến một phần tử của danh sách là thing.

Một định nghĩa hàm bao gồm một hoặc nhiều phương trình khớp với các đầu vào có thể cho hàm đó. Bạn có thể thấy cách điều này hoạt động cho danh sách nếu bạn triển khai allLengths bằng cách kiểm tra danh sách trực tiếp, thay vì sử dụng map.

Listing 3.1.
Calculating word lengths by pattern matching on the list (WordLength.idr)

Để xem chi tiết cách xây dựng định nghĩa này, bạn sẽ xây dựng nó một cách tương tác trong Atom. Mỗi bước có thể được phân loại một cách rộng rãi là Loại (tạo ra hoặc kiểm tra một loại), Định nghĩa (tạo một định nghĩa hoặc phân tách nó thành các điều khoản riêng biệt), hoặc Cải thiện (nâng cao một định nghĩa bằng cách bổ sung một chỗ trống hoặc làm cho loại của nó chính xác hơn).

Type— First, start up Atom and create a WordLength.idr file containing the type declaration for allLengths. That’s only the following:

allLengths : List String -> List Nat

You should also start up an Idris REPL in a separate terminal so that you can type-check and test your definition:

$ idris WordLength.idr ____ __ _ / _/___/ /____(_)____ / // __ / ___/ / ___/ Version 1.0 _/ // /_/ / / / (__ ) http://www.idris-lang.org/ /___/\__,_/_/ /_/____/ Type :? for help Idris is free software with ABSOLUTELY NO WARRANTY. For details type :warranty. Holes: Main.allLengths *WordLength>

Define— In Atom, move the cursor over the name allLengths and press Ctrl-Alt-A. This will add a skeleton definition, and your editor buffer should now contain the following:
```
allLengths : List String -> List Nat allLengths xs = ?allLengths_rhs
```
The skeleton definition is always a clause with the appropriate number of arguments listed on the left side of the =, and with a hole on the right side. Idris uses various heuristics to choose initial names for the arguments. By convention, Idris chooses default names of xs, ys, or zs for Lists.
Type— You can check the types of holes in Atom by pressing Ctrl-Alt-T with the cursor over the hole you want to check. If you check the type of the allLengths_rhs hole, you should see this:
```
 xs : List String -------------------------------------- allLengths_rhs : List Nat
```
Define— You’ll write this definition by inspecting the list argument, named xs, directly. This means that for every form the list can take, you need to explain how to measure word lengths when it’s in that form. To tell the editor that you want to inspect the first argument, press Ctrl-Alt-C in Atom with the cursor over the variable xs in the first argument position. This expands the definition to give the two forms that the argument xs could take:
```
allLengths : List String -> List Nat allLengths [] = ?allLengths_rhs_1 allLengths (x :: xs) = ?allLengths_rhs_2
```
These are the two canonical forms of a list. That is, every list must be in one of these two forms: it can either be empty (in the form []), or it can be non-empty, containing a head element and the rest of the list (in the form (x :: xs)). It’s a good idea at this point to rename x and xs to something more meaningful than these default names:
```
allLengths : List String -> List Nat allLengths [] = ?allLengths_rhs_1 allLengths (word :: words) = ?allLengths_rhs_2
```
In each case, there’s a new hole on the right side to fill in. You can check the types of these holes; type checking gives the expected return type and the types of any local variables. For example, if you check the type of allLengths_rhs_2, you’ll see the types of the local variables word and words, as well as the expected return type:
```
 word : String words : List String -------------------------------------- allLengths_rhs_2 : List Nat
```
Refine— Idris has now told you which patterns are needed. Your job is to complete the definition by filling in the holes on the right side. In the case where the input is the empty list, the output is also the empty list, because there are no words for which to measure the length:
```
allLengths [] = []
```
Refine— In the case where the input is non-empty, there’s a word as the first element (word) followed by the remainder of the list (words). You need to return a list with the length of word as its first element. For the moment, you can add a new hole (?rest) for the remainder of the list:
```
allLengths : List String -> List Nat allLengths [] = [] allLengths (word :: words) = length word :: ?rest
```
You can even test this incomplete definition at the REPL. Note that the REPL doesn’t reload files automatically, because it runs independently of the interactive editing in Atom, so you’ll need to reload explicitly using the :r command:
```
*WordLength> :r Type Checking ./WordLength.idr Holes: Main.rest *WordLength> allLengths ["Hello", "Interactive", "Editors"] 5 :: ?rest : List Nat
```
For the hole rest, you need to calculate the lengths of the words in words. You can do this with a recursive call to allLengths, to complete the definition:
```
allLengths : List String -> List Nat allLengths [] = [] allLengths (word :: words) = length word :: allLengths words
```

Bạn bây giờ có một định nghĩa hoàn chỉnh, mà bạn có thể kiểm tra tại REPL sau khi tải lại:

*WordLength> :r Type Checking ./WordLength.idr *WordLength> allLengths ["Hello", "Interactive", "Editors"] [5, 11, 7] : List Nat

Cũng là một ý tưởng hay để kiểm tra xem Idris có tin rằng định nghĩa này là tổng quát hay không.

*WordLength> :total allLengths Main.allLengths is Total

Totality checking

Khi Idris đã kiểm tra kiểu của một hàm thành công, nó cũng kiểm tra xem nó có tin rằng hàm đó là toàn phần hay không. Nếu một hàm là toàn phần, nó được đảm bảo sẽ tạo ra kết quả cho bất kỳ đầu vào nào có kiểu hợp lệ, trong thời gian hữu hạn. Nhờ vào bài toán dừng, mà chúng ta đã thảo luận trong chương 1, Idris không thể quyết định một cách tổng quát xem một hàm có phải là toàn phần hay không, nhưng bằng cách phân tích cú pháp của một hàm, nó có thể quyết định rằng một hàm là toàn phần trong nhiều trường hợp cụ thể.

Chúng ta sẽ thảo luận về việc kiểm tra toàn bộ chi tiết hơn nhiều trong chương 10 và 11. Trong thời gian này, điều quan trọng là biết rằng Idris sẽ coi một hàm là toàn bộ nếu

It has clauses that cover all possible well-typed inputs
All recursive calls converge on a base case

Như bạn sẽ thấy trong chương 11, định nghĩa về tính toàn vẹn cũng cho phép các chương trình tương tác chạy vô thời hạn, chẳng hạn như máy chủ và vòng lặp tương tác, với điều kiện chúng tiếp tục tạo ra kết quả trung gian trong khoảng thời gian hữu hạn.

Idris tin rằng allLengths là tổng quát vì có các điều khoản cho tất cả các đầu vào đúng kiểu có thể, và đối số cho cuộc gọi đệ quy đến allLengths nhỏ hơn (nghĩa là, gần với trường hợp cơ bản) so với đầu vào.

3.1.3.
Data types and patterns

Khi bạn nhấn Ctrl-Alt-C trong Atom với con trỏ ở phía bên trái của một định nghĩa biến, nó thực hiện một phép chia trường hợp trên biến đó, cung cấp các mẫu khả dĩ mà biến có thể khớp. Nhưng những mẫu này đến từ đâu?

Mỗi kiểu dữ liệu có một hoặc nhiều hàm khởi tạo, là những cách cơ bản để xây dựng giá trị trong kiểu dữ liệu đó và cung cấp các mẫu có thể được khớp cho kiểu dữ liệu đó. Đối với List, có hai:

Nil, which constructs an empty list
::, an infix operator that constructs a list from a head element and a tail

Ngoài ra, như bạn đã thấy trong chương 2, có công thức cú pháp dễ hiểu cho danh sách cho phép danh sách được viết dưới dạng danh sách các giá trị ngăn cách bằng dấu phẩy trong dấu ngoặc vuông. Do đó, Nil cũng có thể được viết là [].

Đối với bất kỳ kiểu dữ liệu nào, bạn có thể tìm thấy các bộ tạo và do đó các mẫu để khớp bằng cách sử dụng :doc tại dấu nhắc REPL:

Idris> :doc List Data type Prelude.List.List : (elem : Type) -> Type Generic lists Constructors: Nil : List elem Empty list (::) : (x : elem) -> (xs : List elem) -> List elem A non-empty list, consisting of a head element and the rest of the list. infixr 7

Documentation in Atom

Bạn có thể lấy tài liệu trực tiếp trong Atom bằng cách nhấn Ctrl-Alt-D, với con trỏ chuột ở tên mà bạn muốn tham khảo tài liệu.

Đối với Bool, ví dụ như :doc cho biết rằng các nhà xây dựng là False và True:

Idris> :doc Bool Data type Prelude.Bool.Bool : Type Boolean Data Type Constructors: False : Bool True : Bool

Vì vậy, nếu bạn viết một hàm nhận một giá trị Bool làm đầu vào, bạn có thể cung cấp các trường hợp rõ ràng cho các đầu vào False và True.

Ví dụ, để viết toán tử XOR, bạn có thể làm theo các bước sau:

Type— Start by giving a type:
```
xor : Bool -> Bool -> Bool
```
Define— Press Ctrl-Alt-A with the cursor over xor to add a skeleton definition:
```
xor : Bool -> Bool -> Bool xor x y = ?xor_rhs
```

Define— Press Ctrl-Alt-C over the x to give the two possible cases for x:

xor : Bool -> Bool -> Bool xor False y = ?xor_rhs_1 xor True y = ?xor_rhs_2

Refine— Complete the definition by filling in the right sides:
```
xor : Bool -> Bool -> Bool xor False y = y xor True y = not y
```

Type checking in Atom

Khi phát triển một hàm, đặc biệt là khi viết các điều khoản bằng tay thay vì sử dụng các tính năng chỉnh sửa tương tác, việc kiểm tra loại dữ liệu những gì bạn đã có cho đến nay có thể là một ý tưởng hay. Lệnh Ctrl-Alt-R sẽ kiểm tra lại bộ đệm hiện tại bằng cách sử dụng quá trình Idris đang chạy. Nếu nó tải thành công, thanh trạng thái của Atom sẽ báo cáo “Tệp đã được tải thành công.”

Kiểu Nat, đại diện cho các số nguyên không âm không giới hạn, cũng được định nghĩa bằng các bộ tạo nguyên thủy. Trong Idris, một số tự nhiên được định nghĩa là bằng không, hoặc nhiều hơn một (tức là, số kế tiếp của) một số tự nhiên khác.

Idris> :doc Nat Data type Prelude.Nat.Nat : Type Natural numbers: unbounded, unsigned integers which can be pattern matched. Constructors: Z : Nat Zero S : Nat -> Nat Successor

Data types and constructors

Các kiểu dữ liệu được định nghĩa theo các bộ dựng của chúng, như bạn sẽ thấy chi tiết trong chương 4. Các bộ dựng của một kiểu dữ liệu là những cách cơ bản để xây dựng kiểu dữ liệu đó, vì vậy trong trường hợp của Nat, mọi giá trị của kiểu Nat phải là hoặc số không hoặc là người kế tiếp của một Nat khác. Số 3, ví dụ, được viết dưới dạng nguyên thủy là S (S (S Z)). Tức là, nó là người kế tiếp (S) của 2 (được viết là S (S Z)).

Do đó, nếu bạn viết một hàm nhận vào một số tự nhiên (Nat) làm đầu vào, bạn có thể cung cấp các trường hợp rõ ràng cho số không (Z) hoặc một số lớn hơn không (S k, trong đó k là bất kỳ số không âm nào). Ví dụ, để viết một hàm isEven trả về True nếu một số tự nhiên đầu vào chia hết cho 2, và trả về False nếu không, bạn có thể định nghĩa nó một cách đệ quy (nếu không hiệu quả) như sau:

Type— Start by giving a type:
```
isEven : Nat -> Bool
```
Define— Press Ctrl-Alt-A to add a skeleton definition:
```
isEven : Nat -> Bool isEven k = ?isEven_rhs
```
Naming conventions

Là một quy tắc đặt tên, Idris chọn k theo mặc định cho các biến có kiểu Nat. Các quy tắc đặt tên có thể được lập trình viên thiết lập khi định nghĩa các kiểu dữ liệu, và bạn sẽ thấy cách làm này trong chương 4. Trong mọi trường hợp, thường là một ý tưởng hay để đổi tên các biến này thành những tên mang tính thông tin hơn.
Define— Press Ctrl-Alt-C over the k to give the two possible cases for k:
```
isEven : Nat -> Bool isEven Z = ?isEven_rhs_1 isEven (S k) = ?isEven_rhs_2
```
To complete the definition, you have to explain what to return when the input is zero (Z) or when the input is non-zero (if the input takes the form S k, then k is a variable standing for a number that’s one smaller than the input).
Refine— Complete the definition by filling in the right sides:
```
isEven : Nat -> Bool isEven Z = True isEven (S k) = not (isEven k)
```
You’ve defined this recursively. Zero is an even number, so you return True for the input Z. If a number is even, its successor is odd, and vice versa, so you return not (isEven k) for the input S k.

Mutually defined functions

Idris xử lý các tệp đầu vào từ trên xuống dưới và yêu cầu các kiểu và hàm phải được định nghĩa trước khi sử dụng. Điều này là cần thiết do những phức tạp phát sinh với các kiểu phụ thuộc, nơi mà việc định nghĩa một hàm có thể ảnh hưởng đến một kiểu.

Tuy nhiên, đôi khi có thể hữu ích để định nghĩa hai hoặc nhiều hàm dựa trên nhau. Điều này có thể đạt được trong một khối hỗn hợp. Ví dụ, bạn có thể định nghĩa isEven dựa trên hàm isOdd, và ngược lại:

mutual isEven : Nat -> Bool isEven Z = True isEven (S k) = isOdd k isOdd : Nat -> Bool isOdd Z = False isOdd (S k) = isEven k

3.2. Adding precision to types: working with vectors

Trong chương 1, chúng ta đã thảo luận về cách việc có kiểu dữ liệu như một cấu trúc ngôn ngữ cấp một cho phép chúng ta định nghĩa các kiểu chính xác hơn. Là một ví dụ, bạn đã thấy cách mà danh sách có thể được đưa ra các kiểu chính xác hơn bằng cách bao gồm số lượng phần tử trong danh sách vào kiểu của nó, cũng như kiểu của các phần tử. Trong Idris, một danh sách bao gồm cả số lượng và kiểu của các phần tử trong kiểu của nó được gọi là vector, được định nghĩa là kiểu dữ liệu Vect. Dưới đây là một số vector ví dụ.

Listing 3.2.
Vectors: lists with lengths encoded in the type (Vectors.idr)

Vect không được định nghĩa trong Prelude, nhưng có thể được làm sẵn có bằng cách nhập mô-đun thư viện Data.Vect. Các mô-đun được nhập bằng một câu lệnh import ở đầu tệp nguồn:

import Data.Vect

Packages: prelude and base

Các mô-đun Idris có thể được kết hợp thành các gói, từ đó các mô-đun riêng lẻ có thể được nhập vào. Prelude được định nghĩa trong một gói gọi là prelude, từ đó tất cả các mô-đun được nhập tự động. Các chương trình Idris cũng có quyền truy cập vào một gói gọi là base, định nghĩa một số cấu trúc dữ liệu và thuật toán thường hữu ích, bao gồm Vect, nhưng các mô-đun từ gói này phải được nhập một cách rõ ràng. Tài liệu cập nhật cho các gói phân phối cùng với Idris có sẵn tại www.idris-lang.org/documentation.

3.2.1.
Refining the type of allLengths

Để xem cách Vect hoạt động, bạn có thể hoàn thiện kiểu của hàm allLengths từ phần 3.1.2 để sử dụng Vect thay vì List, và định nghĩa lại hàm này.

Để làm điều đó, hãy tạo một tệp nguồn mới có tên là WordLength_vec.idr chỉ chứa dòng import Data.Vect, và tải nó vào REPL. Bạn sau đó có thể kiểm tra tài liệu cho Vect:

*WordLength_vec> :doc Vect Data type Data.Vect.Vect : Nat -> Type -> Type Vectors: Generic lists with explicit length in the type Constructors: Nil : Vect 0 a Empty vector (::) : (x : a) -> (xs : Vect k a) -> Vect (S k) a A non-empty vector of length S k, consisting of a head element and the rest of the list, of length k. infixr 7

Lưu ý rằng nó có cùng các hàm tạo như List, nhưng chúng có các kiểu khác nhau để đưa ra chiều dài rõ ràng. Chiều dài được cho dưới dạng Nat, vì chúng không thể âm.

The type of Nil explicitly states that the length is Z (displayed as the numeric literal 0 here).
The type of :: explicitly states that the length is S k, given an element and a tail of length k.

Cũng giống như với List, cú pháp đặc biệt này áp dụng cho một danh sách các giá trị có dấu ngoặc như [1, 2, 3] được dịch sang một chuỗi gồm các ký hiệu :: và Nil: 1 :: 2 :: 3 :: Nil, trong trường hợp này. Thật vậy, cú pháp đặc biệt này áp dụng cho bất kỳ kiểu dữ liệu nào có các bộ tạo được gọi là Nil và ::.

Overloading names

Tên của các hàm khởi tạo cho cả List và Vect là giống nhau, là Nil và ::. Tên có thể được quá tải, với điều kiện rằng các đối tượng khác nhau có cùng tên được định nghĩa trong các không gian tên riêng biệt, điều này thường có nghĩa là các module riêng biệt trong thực tế. Idris sẽ suy luận không gian tên phù hợp từ ngữ cảnh mà tên được sử dụng.

Bạn có thể chỉ định một cách rõ ràng danh sách nào hoặc Vect là cần thiết bằng cách sử dụng:

Idris> the (List _) ["Hello", "There"] ["Hello", "There"] : List String Idris> the (Vect _ _) ["Hello", "There"] ["Hello", "There"] : Vect 2 String

Dấu gạch dưới (_) trong các biểu thức trước đó cho Idris biết rằng bạn muốn nó suy diễn một giá trị cho tham số đó. Bạn có thể sử dụng _ trong một biểu thức bất cứ khi nào có chỉ một giá trị hợp lệ thay cho biểu thức đó. Bạn sẽ tìm hiểu thêm về điều này trong phần 3.4.

Để định nghĩa allLengths bằng cách sử dụng Vect, bạn có thể thực hiện một quy trình tương tự như khi định nghĩa nó bằng List. Sự khác biệt là bạn phải xem xét cách mà độ dài của đầu vào và đầu ra có liên quan đến nhau.

Hình 3.2 cho thấy, trong danh sách đầu ra, luôn có một mục tương ứng với một mục trong danh sách đầu vào. Do đó, bạn có thể chỉ rõ trong kiểu rằng vector đầu ra có độ dài giống như vector đầu vào.

allLengths : Vect len String -> Vect len Nat

Figure 3.2.
Calculating the lengths of words in a list. Notice that each input has a corresponding output, so the length of the output vector is always the same as the length of the input vector.

Độ dài (len) xuất hiện trong đầu vào là một biến ở cấp độ kiểu, đại diện cho độ dài của đầu vào. Bởi vì đầu ra sử dụng cùng một biến ở cấp độ kiểu, nên điều này rõ ràng trong kiểu rằng đầu ra có cùng độ dài với đầu vào. Dưới đây là cách bạn có thể viết hàm:

Type— Create an Atom buffer with the following contents to import Data.Vect and give the type of allLengths:
```
import Data.Vect allLengths : Vect len String -> Vect len Nat
```

Define— As before, create a skeleton definition with Ctrl-Alt-A:

allLengths : Vect len String -> Vect len Nat allLengths xs = ?allLengths_rhs

Define— As before, press Ctrl-Alt-C over the xs to tell Idris that you’d like to define the function by pattern matching on xs:

allLengths : Vect len String -> Vect len Nat allLengths [] = ?allLengths_rhs_1 allLengths (x :: xs) = ?allLengths_rhs_2

As before, it’s a good idea at this point to rename the variables x and xs to something more meaningful:

allLengths : Vect len String -> Vect len Nat allLengths [] = ?allLengths_rhs_1 allLengths (word :: words) = ?allLengths_rhs_2

Type— If you now inspect the types of the holes allLengths_rhs_1 and allLengths_rhs_2, you’ll see more information than in the List version, because the types are more precise. For example, in allLengths_rhs_1 you can see that the only valid result is a vector with zero elements:
```
-------------------------------------- allLengths_rhs_1 : Vect 0 Nat
```
In allLengths_rhs_2 you can see how the lengths of the pattern variables and output relate to each other, given some natural number n:
```
 word : String k : Nat words : Vect k String -------------------------------------- allLengths_rhs_2 : Vect (S k) Nat
```
That is, in the pattern (word :: words), word is a String, words is a vector of kStrings, and for the output you need to provide a vector of Nat of length 1 + k, represented as S k.
Refine— For allLengths_rhs_1, there’s only one vector that has length zero, which is the empty vector, so there’s only one value you can use to refine the definition by filling in the hole:
```
allLengths : Vect len String -> Vect len Nat allLengths [] = [] allLengths (word :: words) = ?allLengths_rhs_2
```
Refine— For allLengths_rhs_2, the required type is Vect (S k) Nat, so the result must be a non-empty vector (using ::). Also, you can make a value of type Vect k Nat by calling allLengths recursively. You can leave a hole for the first element in the resulting list, refining the definition by hand as follows:
```
allLengths : Vect len String -> Vect len Nat allLengths [] = [] allLengths (word :: words) = ?wordlen :: allLengths words
```
You still have one hole in this result, ?wordlen, which will be the length of the first word:
```
 word : String k : Nat words : Vect k String -------------------------------------- wordlen : Nat
```

Refine— To complete the definition, fill in the remaining hole by calculating the length of the word x:

allLengths : Vect len String -> Vect len Nat allLengths [] = [] allLengths (word :: words) = length word :: allLengths words

Loại chính xác hơn, mô tả cách mà độ dài của đầu vào và đầu ra liên quan đến nhau, có nghĩa là chế độ chỉnh sửa tương tác có thể cho bạn biết nhiều hơn về các biểu thức bạn đang tìm kiếm. Bạn cũng có thể tự tin hơn rằng chương trình hoạt động như mong muốn bằng cách loại trừ bất kỳ chương trình nào không bảo toàn độ dài thông qua kiểm tra kiểu.

Nat and data structures

Bạn có thể nhận thấy một sự tương ứng trực tiếp giữa các constructor của Vect và các constructor của Nat. Khi bạn thêm một phần tử vào một Vect bằng ::, bạn thêm một constructor S vào độ dài của nó. Trên thực tế, việc nắm bắt kích thước của các cấu trúc dữ liệu như thế này là một việc làm rất phổ biến của Nat.

Để minh họa cách các quy tắc kiểu chính xác loại trừ một số chương trình không chính xác, hãy xem xét việc triển khai sau của allLengths, sử dụng List thay vì Vect:

allLengths : List String -> List Nat allLengths xs = []

Điều này được kiểu hóa tốt và sẽ được Idris chấp nhận, nhưng nó sẽ không hoạt động như dự định vì không có đảm bảo rằng danh sách đầu ra có một mục tương ứng với mỗi mục trong đầu vào. Mặt khác, chương trình sau với kiểu chính xác hơn không được kiểu hóa tốt và sẽ không được Idris chấp nhận:

allLengths : Vect n String -> Vect n Nat allLengths xs = []

Điều này dẫn đến loại lỗi sau, trong đó nói rằng một vector rỗng đã được cung cấp khi một vector có độ dài n là cần thiết:

WordLength_vec.idr:4:14:When checking right hand side of allLengths: Type mismatch between Vect 0 Nat (Type of []) and Vect n Nat (Expected type)

Giống như với phiên bản dựa trên danh sách trước đó của allLengths, bạn có thể kiểm tra rằng định nghĩa mới của bạn là tổng quát tại REPL:

*WordLength_vec> :total allLengths Main.allLengths is Total

Nếu, ví dụ, bạn loại bỏ trường hợp cho danh sách rỗng, bạn sẽ có một định nghĩa kiểu tốt nhưng không đầy đủ:

allLengths : Vect len String -> Vect len Nat allLengths (word :: words) = length word :: allLengths words

Khi bạn kiểm tra điều này cho tính toàn vẹn, bạn sẽ thấy điều này:

*WordLength_vec> :total allLengths Main.allLengths is not total as there are missing cases

Totality annotations

Để tăng cường sự tự tin về độ chính xác của một hàm, bạn có thể chú thích trong mã nguồn rằng một hàm phải là tổng quát. Ví dụ, bạn có thể viết như sau:

total allLengths : Vect len String -> Vect len Nat allLengths [] = [] allLengths (word :: words) = length word :: allLengths words

Từ khóa "total" trước phần khai báo kiểu có nghĩa là Idris sẽ báo lỗi nếu định nghĩa không phải là tổng quát. Ví dụ, nếu bạn loại bỏ trường hợp allLengths [] thì đây là thông báo mà Idris sẽ hiển thị:

WordLength_vec.idr:5:1: Main.allLengths is not total as there are missing cases

3.2.2.
Type-directed search: automatic refining

Sau bước 3 ở phần trước, bạn đã có các mẫu cho allLengths và holes cho các mặt bên phải, mà bạn đã cung cấp bằng cách tinh chỉnh trực tiếp:

allLengths : Vect n String -> Vect n Nat allLengths [] = ?allLengths_rhs_1 allLengths (word :: words) = ?allLengths_rhs_2

Hãy xem xét lại các loại và các biến cục bộ cho các lỗ allLengths_rhs_1 và allLengths_rhs_2:

-------------------------------------- allLengths_rhs_1 : Vect 0 Nat word : String k : Nat words : Vect k String -------------------------------------- allLengths_rhs_2 : Vect (S k) Nat

Bằng cách nhìn kỹ vào các kiểu, bạn có thể thấy cách để xây dựng các giá trị lấp đầy những khoảng trống này. Nhưng không chỉ bạn có nhiều thông tin hơn ở đây, mà Idris cũng vậy!

Nếu có đủ thông tin trong kiểu, Idris có thể tìm kiếm một biểu thức hợp lệ thỏa mãn kiểu đó. Trong Atom, hãy nhấn Ctrl-Alt-S trên lỗ allLengths_rhs_1, và bạn sẽ thấy rằng định nghĩa đã thay đổi:

allLengths : Vect n String -> Vect n Nat allLengths [] = [] allLengths (word :: words) = ?allLengths_rhs_2

Bởi vì chỉ có một giá trị duy nhất cho một vector có độ dài bằng không, Idris đã tự động tinh chỉnh điều này.

Bạn cũng có thể thử tìm kiếm biểu thức trên lỗ allLengths_rhs_2. Nhấn Ctrl-Alt-S khi con trỏ ở trên allLengths_rhs_2, và bạn sẽ thấy điều này:

allLengths : Vect n String -> Vect n Nat allLengths [] = [] allLengths (word :: words) = 0 :: allLengths words

Loại yêu cầu là Vect (S k) Nat, vì vậy, như trước đây, Idris đã nhận ra rằng kết quả duy nhất có thể là một vector không rỗng. Nó cũng nhận ra rằng nó có thể tìm thấy một giá trị có kiểu Vect k Nat bằng cách gọi đệ quy allLengths trên các từ.

Đối với Nat ở đầu của vector, Idris đã tìm thấy giá trị đầu tiên thỏa mãn kiểu, 0, nhưng điều này không hoàn toàn là thứ bạn muốn, vì vậy bạn có thể thay thế nó bằng một khoảng trống—?vecthead:

allLengths : Vect n String -> Vect n Nat allLengths [] = [] allLengths (word :: words) = ?vecthead :: allLengths words

Kiểm tra loại của ?vecthead xác nhận rằng bạn đang tìm kiếm một Nat:

 word : String k : Nat words : Vect k String -------------------------------------- vecthead : Nat

Như trước đây, bạn có thể hoàn thành định nghĩa bằng cách điền từ có độ dài vào khoảng trống này. Vì vậy, không chỉ loại chính xác hơn mang lại cho bạn nhiều sự tự tin hơn về độ chính xác của chương trình và cung cấp cho bạn nhiều thông tin hơn khi viết chương trình, mà nó còn cung cấp cho Idris một số thông tin, cho phép nó viết một phần lớn của chương trình cho bạn.

3.2.3.
Type, define, refine: sorting a vector

Đối với tất cả các hàm bạn đã viết cho đến nay trong chương này, bạn đã tuân theo quy trình này:

Write a type.
Create a skeleton definition.
Pattern match on an argument.
Fill in the holes on the right side with a combination of type-driven expression search and refining holes by hand.

Thường thì sẽ có một chút công việc thêm, tuy nhiên. Ví dụ, bạn có thể thấy cần tạo thêm các hàm trợ giúp, kiểm tra các kết quả trung gian, hoặc tinh chỉnh kiểu dữ liệu mà bạn đã cung cấp ban đầu cho một hàm.

Bạn có thể thấy điều này trong thực tiễn bằng cách tạo một hàm trả về phiên bản đã sắp xếp của một vector đầu vào. Bạn có thể sử dụng thuật toán sắp xếp chèn, đây là một thuật toán sắp xếp đơn giản dễ dàng được triển khai theo phong cách hàm, được mô tả một cách không chính thức như sau:

Given an empty vector, return an empty vector.
Given the head and tail of a vector, sort the tail of the vector and then insert the head into the sorted tail such that the result remains sorted.

Bạn có thể viết điều này một cách tương tác, bắt đầu với định nghĩa khung được hiển thị trong danh sách 3.3. Mở một bộ đệm Atom và đặt mã này vào một tệp có tên là VecSort.idr. Hãy nhớ rằng bạn có thể tạo định nghĩa khung của insSort từ loại bằng cách nhấn Ctrl-Alt-A.

Listing 3.3.
A skeleton definition of `insSort` on vectors with an initial type (VecSort.idr)

Khi bạn làm việc qua quá trình này, tôi khuyên bạn nên kiểm tra các loại của từng lỗ hổng xuất hiện bằng cách sử dụng Ctrl-Alt-T, và đảm bảo rằng bạn hiểu các loại của các biến và lỗ hổng.

Development workflow

Thường thì việc mở một cửa sổ Atom để chỉnh sửa tệp một cách tương tác và một cửa sổ terminal với REPL để kiểm tra, đánh giá, tra cứu tài liệu, v.v. là rất hữu ích.

Sau khi đã viết kiểu cho hàm này, hãy triển khai nó bằng cách làm theo các bước sau:

Define— Case-split on xs with Ctrl-Alt-C, leading to this:

insSort : Vect n elem -> Vect n elem insSort [] = ?insSort_rhs_1 insSort (x :: xs) = ?insSort_rhs_2

Refine— Try an expression search on ?insSort_rhs_1, leading to this:
```
insSort : Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = ?insSort_rhs_2
```
A sorted empty vector is itself an empty vector, as expected.
Refine— Trying an expression search on ?insSort_rhs_2 is, unfortunately, less effective:
```
insSort : Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = x :: xs
```
Although Idris knows how long the vector should be, and it has local variables of the correct types, the overall type of insSort isn’t precise enough for Idris to fill in the hole with the program you intend.

Expression search

Như ví dụ này chứng minh, mặc dù tìm kiếm biểu thức thường có thể dẫn bạn đến một hàm hợp lệ, nhưng nó không thể thay thế cho việc hiểu cách chương trình hoạt động! Bạn cần phải hiểu thuật toán, nhưng bạn có thể sử dụng tìm kiếm biểu thức để giúp điền vào các chi tiết.
Define— When you’re writing a function over a recursive data type, it’s often effective to make recursive calls to the recursive parts of the structure. Here, you can sort the tail with a recursive call to insSort xs and bind the result to a locally defined variable:
```
insSort : Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = let xsSorted = insSort xs in ?insSort_rhs_2
```
Type— In ?insSort_rhs_2 you’re going to insert the head x into the sorted tail, xsSorted. Because this is going to be a little more complex, you can lift the hole to a top-level definition by pressing Ctrl-Alt-L with the cursor over ?-insSort_rhs_2, which leads to the following:
```
insSort_rhs_2 : (x : elem) -> (xs : Vect k elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insSort : Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = let xsSorted = insSort xs in insSort_rhs_2 x xs xsSorted
```
This has created a new top-level function with a new type but no implementation, and it has replaced the hole with a call to the new function. The arguments to the new function are the local variables that were in scope in the hole ?insSort_rhs_2.
Refine— Once you realize that the job of the new function is to insert x into the xsSorted vector, you can edit the name and type of insSort_rhs_2 to reflect this. You can remove the arguments that you aren’t going to need:
```
insert : (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insSort : Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = let xsSorted = insSort xs in insert x xsSorted
```
Lifting Definitions

Khi nâng cấp một định nghĩa bằng Ctrl-Alt-L, Idris sẽ tạo ra một định nghĩa mới với cùng tên như lỗ hổng, sử dụng tất cả các biến cục bộ trong kiểu được tạo ra. Trong trường hợp này, bạn biết rằng bạn sẽ không cần tất cả chúng, vì vậy bạn có thể chỉnh sửa để bỏ đi đối số xs không cần thiết.

Define— You now have to define insert. Again, create a skeleton definition:

insert : (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x xsSorted = ?insert_rhs

Then case-split on xsSorted, leading to this:

insert : (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = ?insert_rhs_1 insert x (y :: xs) = ?insert_rhs_2

Refine— An expression search on insert_rhs_1 leads to the following:
```
insert : (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = ?insert_rhs_2
```
This works because Idris knows it’s looking for a vector with one element of type elem, and the only thing available with type elem is x.
Refine— For the (y :: xs) case, with the hole ?insert_rhs_2, you have a problem. There are two cases to consider:
- If x < y, the result should be x :: y :: xs, because the result won’t be ordered if x is inserted after y.
- Otherwise, the result should begin with y, and then have x inserted into the tail xs.
Your problem is that you know nothing about the element type elem. You need to constrain it so that you know you can compare elements of type elem. You can refine the type of insert (and correspondingly insSort) so that you can do the necessary comparison:
```
insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = ?insert_rhs_2 insSort : Ord elem => Vect n elem -> Vect n elem insSort [] = [] insSort (x :: xs) = let xsSorted = insSort xs in insert x xsSorted
```
Remember from chapter 2 that you constrain generic types by placing constraints such as Ord elem before => in the type. You’ll see more about this in chapter 7.
Define— You now need to check x < y and act on the result. One way to do this is with an if...then...else construct:
```
insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = if x < y then x :: y :: xs else y :: insert x xs
```
Alternatively, you can use interactive editing to give more structure to the definition, and insert a case construct to match on an intermediate result. Press Ctrl-Alt-M with the cursor over ?insert_rhs_2. This introduces a new case expression with a placeholder for the value to be inspected (so the function won’t type-check yet):
```
insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = case _ of case_val => ?insert_rhs_2
```
The _ stands for an expression you need to provide in order for the function to type-check successfully. You’ll need to fill in the _ with the expression you want to match:
```
insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = case x < y of case_val => ?insert_rhs_2
```

Define— You can now case-split on case_val in the usual way, with Ctrl-Alt-C, leading to this:

insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = case x < y of False => ?insert_rhs_1 True => ?insert_rhs_3

Refine— Finally, you complete the implementation by filling in the new holes insert_rhs_1 and insert_rhs_3. Unfortunately, expression search won’t help you much here because there’s not enough information in the type, so you need to fill these in by hand:
```
insert : Ord elem => (x : elem) -> (xsSorted : Vect k elem) -> Vect (S k) elem insert x [] = [x] insert x (y :: xs) = case x < y of False => y :: insert x xs True => x :: y :: xs
```

Khi định nghĩa hoàn tất, bạn có thể kiểm tra nó tại REPL, như thế này:

*VecSort> insSort [1,3,2,9,7,6,4,5,8] [1, 2, 3, 4, 5, 6, 7, 8, 9] : Vect 9 Integer

Remember totality checking!

“Đừng quên kiểm tra rằng insSort là tổng: ”

*VecSort> :total insSort Main.insSort is Total

Đó là một thói quen tốt để kiểm tra rằng các hàm bạn định nghĩa là tổng quát. Nếu một hàm đúng kiểu nhưng không tổng quát, nó có thể vẫn hoạt động khi bạn kiểm tra, nhưng vẫn có thể có một lỗi tinh vi nào đó với một số đầu vào bất thường, chẳng hạn như thiếu mẫu hoặc khả năng không kết thúc.

Tóm lại, sau quá trình xác định kiểu và tinh chỉnh, bạn đã thực hiện các bước sau:

Written a type for insSort.
Tried to define insSort until you encountered the need to insert, which you lifted to a new top-level definition with its own type.
Tried to define insert until you encountered the need to compare, at which point you refined the types to support the ordering constraint on elem.
Continued to define insert using the refined type, and hence completed the implementation of insSort.

Exercises

Để kết luận phần này, đây là một số bài tập để kiểm tra sự hiểu biết của bạn về chế độ chỉnh sửa tương tác và khớp mẫu trên List và Vect.

Các hàm sau đây, hoặc một biến thể nào đó của chúng, được định nghĩa trong Prelude hoặc trong Data.Vect:

length : List a -> Nat
reverse : List a -> List a
map : (a -> b) -> List a -> List b
map : (a -> b) -> Vect n a -> Vect n b

Đối với mỗi cái trong số chúng, hãy định nghĩa phiên bản của riêng bạn bằng cách sử dụng chỉnh sửa tương tác trong Atom. Lưu ý rằng bạn sẽ cần sử dụng những cái tên khác nhau (chẳng hạn như my_length, my_reverse, my_map) để tránh xung đột với các tên trong Prelude. Bạn có thể kiểm tra các câu trả lời của mình tại REPL như sau:

*ex_3_2> my_length [1..10] 10 : Nat *ex_3_2> my_reverse [1..10] [10, 9, 8, 7, 6, 5, 4, 3, 2, 1] : List Integer *ex_3_2> my_map (* 2) [1..10] [2, 4, 6, 8, 10, 12, 14, 16, 18, 20] : List Integer *ex_3_2> my_vect_map length ["Hot", "Dog", "Jumping", "Frog"] [3, 3, 7, 4] : Vect 4 Nat

Đừng quên kiểm tra rằng các định nghĩa của bạn là toàn phần!

3.3. Example: type-driven development of matrix functions

Lý do chính bạn có thể sử dụng vector, với độ dài được chỉ rõ trong kiểu dữ liệu, thay vì sử dụng danh sách, là để có được độ dài của các vector giúp hướng dẫn bạn đến một hàm làm việc nhanh hơn. Điều này đặc biệt hữu ích khi bạn làm việc với các vector hai chứ danh. Những cái này, lại có thể hữu ích cho việc thực hiện các phép toán trên ma trận, có nhiều ứng dụng trong lập trình, chẳng hạn như đồ họa 3D.

Ma trận, trong toán học, là một mảng hình chữ nhật của các số được sắp xếp theo hàng và cột. Hình 3.3 cho thấy một ví dụ về ma trận 3 × 4 dưới dạng ký hiệu toán học và trong ký hiệu Idris dưới dạng vector của các vector. Lưu ý rằng khi đại diện một ma trận dưới dạng các vector lồng nhau, kích thước của ma trận trở nên rõ ràng trong kiểu dữ liệu.

Figure 3.3.
Representation of a matrix as two-dimensional vectors. On the left, the matrix is in mathematical notation. The same matrix is represented in Idris on the right.

3.3.1.
Matrix operations and their types

Khi thực hiện các phép toán trên ma trận, chẳng hạn như cộng và nhân, việc kiểm tra rằng kích thước của các vectơ bạn đang làm việc là phù hợp với các phép toán là rất quan trọng. Ví dụ:

When adding matrices, each matrix must have exactly the same dimensions. Addition works by adding corresponding elements in each matrix. For example, you can add two 3 × 2 matrices as follows:
The following addition of a 2 × 2 matrix to a 3 × 2 matrix is invalid because there are no corresponding elements in the third row: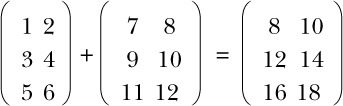
So, the type of matrix addition could be as follows: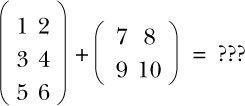
```
addMatrix : Num numType => Vect rows (Vect cols numType) -> Vect rows (Vect cols numType) -> Vect rows (Vect cols numType)
```
In other words, for some numeric type numType, adding a rows × cols matrix to a rows × cols matrix results in a rows × cols matrix.
When multiplying matrices, the number of columns in the left matrix must be the same as the number of rows in the right matrix. Then, multiplication works as follows:

Here, multiplying a 3 × 2 matrix by a 2 × 4 matrix results in a 3 × 4 matrix. The value in row x, column y in the result is the sum of the product of corresponding elements in row x of the left input, and column y of the right input. So the type of matrix multiplication could be as follows:
```
multMatrix : Num numType => Vect n (Vect m numType) -> Vect m (Vect p numType) -> Vect n (Vect p numType)
```
In other words, for some numeric type numType, multiplying an n × m matrix by an m × p matrix results in an n × p matrix.

3.3.2.
Transposing a matrix

Một phép toán hữu ích khi thao tác với ma trận là phép chuyển vị, biến các hàng thành các cột và ngược lại. Ví dụ, một ma trận 3 × 2 trở thành ma trận 2 × 3:

Bạn có thể viết một hàm transposeMat mà, nói chung, chuyển đổi một ma trận m × n thành một ma trận n × m, đại diện cho các ma trận dưới dạng các vector lồng nhau. Như thường lệ, bạn có thể viết hàm một cách tương tác, trong đó mỗi bước được mô tả chung là một trong các loại: kiểu, xác định hoặc tinh chỉnh. Từ điểm này, tôi sẽ giả định rằng bạn cảm thấy thoải mái với các lệnh tương tác trong Atom, và tôi sẽ mô tả quy trình tổng thể dựa trên kiểu thay vì các chi tiết cụ thể về việc xây dựng hàm.

Type— Begin by giving a type for transposeMat:
```
transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem)
```
For matrix arithmetic, in the types of addMatrix and multMatrix, you need to constrain the element type to be numeric. Here, though, the element type of the matrix, elem, could be anything. You’re not going to inspect it or use it at any point in the implementation of transposeMat; you merely change the rows to columns and columns to rows.

Define— Create a skeleton definition, and then case-split on the input vector:

transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem) transposeMat [] = ?transposeMat_rhs_1 transposeMat (x :: xs) = ?transposeMat_rhs_2

Type— When Idris creates new holes, either from a case split or an incomplete result of an expression search, it’s always a good idea to inspect the types of those holes to get some insight into how to proceed. First, take a look at the type of ?transposeMat_rhs_1:
```
 elem : Type n : Nat -------------------------------------- transposeMat_rhs_1 : Vect n (Vect 0 elem)
```
Here, you’re trying to convert a 0 × n vector into an n × 0 vector, so you need to create n copies of an empty vector. We’ll return to this case later; for now, you can rename the hole to createEmpties and lift it to a top-level function with Ctrl-Alt-L:
```
createEmpties : Vect n (Vect 0 elem) transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem) transposeMat [] = createEmpties transposeMat (x :: xs) = ?transposeMat_rhs_2
```

Type— Look at the type of ?transposeMat_rhs_2:

 elem : Type n : Nat x : Vect n elem k : Nat xs : Vect k (Vect n elem) -------------------------------------- transposeMat_rhs_2 : Vect n (Vect (S k) elem)

You have xs, which is a k × n matrix, and you need to make an n × (S k) matrix.

Define— One insight you need here is that it’s likely easier to build an n × (S k) matrix from an n × k matrix, because at least one of the dimensions is correct. You can create such a matrix by transposing xs:
```
transposeMat (x :: xs) = let xsTrans = transposeMat xs in ?transposeMat_rhs_2
```
Type— You can also lift ?transposeMat_rhs_2 to a top-level function, renaming it transposeHelper. This results in the following:
```
transposeHelper : (x : Vect n elem) -> (xs : Vect k (Vect n elem)) -> (xsTrans : Vect n (Vect k elem)) -> Vect n (Vect (S k) elem)
```
The type for transposeHelper is generated from the types of the local variables you have access to: x, xs, and xsTrans. It will take these variables as inputs, and produce a Vect n (Vect (S k) elem) as output.
Type— At this stage, it’s good to look more closely at the types of the variables x, xs, and xsTrans and try to use these types to visualize what you need to do to complete transposeMat. For the sake of visualization, let’s take n = 4 and k = 2. Figure 3.4 shows an original two-dimensional vector, of the form (x :: xs), where x is the first row and xs is the rest of the rows, built with these dimensions. It identifies the components x and xs, and it shows the result of transposing xs and the expected result of the whole operation.
Figure 3.4.
The components of the vector you’re transposing (x and xs), along with the result of transposing xs, and the expected overall result

What you need to do, therefore, is add each element of x to the vector in the corresponding element of xsTrans; you won’t need xs in transposeHelper. If you delete this by hand in the type of transposeHelper and the application in transposeMat, you get this: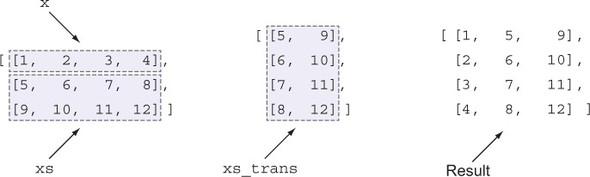
```
transposeHelper : (x : Vect n elem) -> (xsTrans : Vect n (Vect k elem)) -> Vect n (Vect (S k) elem) transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem) transposeMat [] = createEmpties transposeMat (x :: xs) = let xsTrans = transposeMat xs in transposeHelper x xsTrans
```
Define— To implement transposeHelper, you can add a skeleton definition, pattern match on x and xsTrans, and then use expression search to complete the definition. There’s enough information for Idris to fill in the details itself:
```
transposeHelper : (x : Vect n elem) -> (xsTrans : Vect n (Vect k elem)) -> Vect n (Vect (S k) elem) transposeHelper [] [] = [] transposeHelper (x :: xs) (y :: ys) = (x :: y) :: transposeHelper xs ys
```
Rather than typing this in directly, try to build it using the interactive commands. It’s possible to write this function from the type using only Ctrl-Alt-A, Ctrl-Alt-C, Ctrl-Alt-S, and cursor movements.

Case splitting on vectors

Nếu bạn chia trường hợp trên x và sau đó chia trường hợp trên xsTrans, hãy lưu ý rằng Idris chỉ đưa ra một mẫu khả thi cho xsTrans. Điều này là bởi vì kiểu của x và xsTrans cho thấy cả hai phải có cùng độ dài.
Define— All that remains is to implement createEmpties. You can implement this using a library function, replicate:
```
*transpose> :doc Vect.replicate Data.Vect.replicate : (n : Nat) -> (x : a) -> Vect n a Repeat some value n times Arguments: n : Nat -- the number of times to repeat it x : a -- the value to repeat
```
If you create a skeleton definition of createEmpties from its type, you’ll see the following:
```
createEmpties : Vect n (Vect 0 elem) createEmpties = ?createEmpties_rhs
```
You need to call replicate to build a vector of n empty lists. Unfortunately, because there are no local variables available from the patterns on the left side, the natural definition results in an error message:
```
createEmpties : Vect n (Vect 0 elem) createEmpties = replicate n [] -- "No such variable n"
```
The problem is that n is a type-level variable, and not accessible to the definition of createEmpties. Shortly, in section 3.4, you’ll see how to handle type-level variables in general, and how you might write createEmpties directly. For the moment, because the type dictates that there’s only one valid value for the length argument to replicate, you can use an underscore instead:
```
createEmpties : Vect n (Vect 0 elem) createEmpties = replicate _ []
```

Việc triển khai transposeMat đã hoàn tất. Để tham khảo, định nghĩa đầy đủ được cung cấp trong danh sách 3.4. Bạn có thể kiểm tra nó tại REPL:

*transpose> transposeMat [[1,2], [3,4], [5,6]] [[1, 3, 5], [2, 4, 6]] : Vect 2 (Vect 3 Integer)

Listing 3.4.
Complete definition of matrix transposition (Matrix.idr)

createEmpties : Vect n (Vect 0 elem) createEmpties = replicate _ [] transposeHelper : (x : Vect n elem) -> (xsTrans : Vect n (Vect k elem)) -> Vect n (Vect (S k) elem) transposeHelper [] [] = [] transposeHelper (x :: xs) (y :: ys) = (x :: y) :: transposeHelper xs ys transposeMat : Vect m (Vect n elem) -> Vect n (Vect m elem) transposeMat [] = createEmpties transposeMat (x :: xs) = let xsTrans = transposeMat xs in transposeHelper x xsTrans

Code reuse

Khi xây dựng một định nghĩa một cách tương tác bằng quy trình xác định - tinh chỉnh kiểu, tốt nên chú ý đến các phần của định nghĩa có thể được làm cho tổng quát hơn, hoặc có thể được thực hiện bằng cách sử dụng các hàm thư viện hiện có.

Ví dụ, transposeHelper có cấu trúc rất giống với hàm thư viện zipWith, hàm này áp dụng một hàm cho các phần tử tương ứng trong hai vector và được định nghĩa như sau:

zipWith : (a -> b -> c) -> Vect n a -> Vect n b -> Vect n c zipWith f [] [] = [] zipWith f (x :: xs) (y :: ys) = f x y :: zipWith f xs ys

Exercises

Reimplement transposeMat using zipWith instead of transposeHelper. You can test your answer at the REPL as follows:
```
*ex_3_3_3> transposeMat [[1,2], [3,4], [5,6]] [[1, 3, 5], [2, 4, 6]] : Vect 2 (Vect 3 Integer)
```
Implement addMatrix : Num a => Vect n (Vect m a) -> Vect n (Vect m a) -> Vect n (Vect m a). You can test your answer at the REPL as follows:
```
*ex_3_3_3> addMatrix [[1,2], [3,4]] [[5,6], [7,8]] [[6, 8], [10, 12]] : Vect 2 (Vect 2 Integer)
```
Implement a function for multiplying matrices, following the description given in section 3.3.1. Hint: This definition is quite tricky and involves multiple steps. Consider the following:
- You have a left matrix of dimensions n × m, and a right matrix of dimensions m × p. A good start is to use transposeMat on the right matrix.
- Remember that you can use Ctrl-Alt-L to lift holes to top-level functions.
- Remember to pay close attention to the types of the local variables and the types of the holes.
- Remember to use Ctrl-Alt-S to search for expressions, and pay close attention to the types of any resulting holes.
You can test your answer at the REPL as follows:
```
*ex_3_3_3> multMatrix [[1,2], [3,4], [5,6]] [[7,8,9,10], [11,12,13,14]] [[29, 32, 35, 38], [65, 72, 79, 86], [101, 112, 123, 134]] : Vect 3 (Vect 4 Integer)
```

3.4. Implicit arguments: type-level variables

Bạn đã thấy một số định nghĩa với các biến ở cấp độ kiểu có thể đại diện cho kiểu hoặc giá trị. Ví dụ:

reverse : List elem -> List elem

Ở đây, elem là một biến ở cấp độ kiểu đại diện cho kiểu của phần tử trong danh sách. Nó xuất hiện hai lần, trong kiểu đầu vào và kiểu trả về, vì vậy kiểu phần tử của mỗi cái phải giống nhau.

append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Ở đây, elem lại là một biến cấp độ kiểu đại diện cho loại phần tử của các vector. n và m là các biến cấp độ kiểu đại diện cho độ dài của các vector đầu vào, và chúng lại được sử dụng trong đầu ra để mô tả cách độ dài của đầu ra liên quan đến độ dài của các đầu vào.

Các biến cấp độ kiểu này không được khai báo ở bất kỳ đâu khác. Bởi vì các kiểu là cấp một, các biến cấp độ kiểu cũng có thể được đưa vào phạm vi và sử dụng trong các định nghĩa. Những biến cấp độ kiểu này được gọi là các tham số ngầm (implicit arguments) của các hàm reverse và append. Trong phần này, bạn sẽ thấy cách các tham số ngầm hoạt động và cách sử dụng chúng trong các định nghĩa.

3.4.1.
The need for implicit arguments

Để minh họa nhu cầu về các tham số ngụ ý, hãy xem xét cách bạn có thể định nghĩa hàm append mà không có chúng. Bạn có thể làm cho các tham số elem, n và m của hàm append trở nên rõ ràng, dẫn đến định nghĩa sau:

append : (elem : Type) -> (n : Nat) -> (m : Nat) -> Vect n elem -> Vect m elem -> Vect (n + m) elem append elem Z m [] ys = ys append elem (S k) m (x :: xs) ys = x :: append elem k m xs ys

Nhưng nếu bạn làm như vậy, bạn cũng sẽ phải chỉ định rõ ràng về kiểu phần tử và độ dài khi gọi append:

*Append_expl> append Char 2 2 ['a','b'] ['c','d'] ['a', 'b', 'c', 'd'] : Vect 4 Char

Xem xét các kiểu của các đối số ['a', 'b'] và ['c', 'd'], chỉ có một giá trị khả thi cho mỗi đối số elem (phải là một Char), n (phải là 2, từ độ dài của ['a', 'b']), và m (cũng phải là 2, từ độ dài của ['c', 'd']). Bất kỳ giá trị nào khác cho bất kỳ đối số nào trong số này sẽ không được kiểu hợp lệ.

Bởi vì có đủ thông tin trong các kiểu của các đối số vector, Idris có thể suy ra giá trị cho các đối số a, n và m. Do đó, bạn có thể viết như sau:

*Append> append _ _ _ ['a','b'] ['c','d'] ['a', 'b', 'c', 'd'] : Vect 4 Char

Implicit values

Một dấu gạch dưới (_) trong một lời gọi hàm có nghĩa là bạn muốn Idris tự động xác định một giá trị ngầm định cho tham số, dựa trên thông tin trong phần còn lại của biểu thức.

*Append> append _ _ _ ['a','b'] ['c','d'] ['a', 'b', 'c', 'd'] : Vect 4 Char

Idris sẽ báo lỗi nếu nó không thể:

*Append> append _ _ _ _ ['c','d'] (input):Can't infer argument n to append, Can't infer explicit argument to append

Ở đây, Idris báo cáo rằng nó không thể xác định độ dài của vector đầu tiên, hoặc chính vector đầu tiên. Khác với dấu chấm, đại diện cho các phần của biểu thức chưa được viết, dấu gạch dưới đại diện cho các phần của biểu thức mà chỉ có một giá trị hợp lệ. Đây là lỗi nếu Idris không thể suy ra một giá trị duy nhất cho một dấu gạch dưới.

Việc sử dụng các tham số ngầm giúp tránh việc phải viết chi tiết một cách rõ ràng mà Idris có thể suy luận được. Việc làm elem, n và m trở thành ngầm trong kiểu của hàm append có nghĩa là bạn có thể tham chiếu đến chúng trực tiếp trong kiểu khi cần thiết, mà không cần phải cung cấp giá trị rõ ràng khi gọi hàm.

3.4.2.
Bound and unbound implicits

Hãy xem lại các loại reverse và append với các tham số ngầm:

reverse : List elem -> List elem append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Các tên elem, n và m được gọi là các ẩn số không ràng buộc. Điều này là vì tên của chúng được sử dụng trực tiếp, mà không được khai báo (hay ràng buộc) ở bất kỳ đâu khác. Bạn cũng có thể viết các loại này như sau:

reverse : {elem : Type} -> List elem -> List elem append : {elem : Type} -> {n : Nat} -> {m : Nat} -> Vect n elem -> Vect m elem -> Vect (n + m) elem

Ở đây, các đối số ngầm định đã được ràng buộc rõ ràng trong kiểu. Ký hiệu {x : S} -> T biểu thị một kiểu hàm nơi đối số dự kiến sẽ được Idris suy ra, chứ không phải được lập trình viên viết trực tiếp.

Khi bạn viết một kiểu với các tham số ngầm không ràng buộc, Idris sẽ tìm kiếm các tên chưa xác định trong kiểu và biến chúng thành các tham số ngầm có ràng buộc. Hãy xem xét ví dụ này:

append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Đầu tiên, Idris xác định rằng elem, n và m chưa được định nghĩa, vì vậy nó tự động viết lại kiểu như sau:

append : {elem : _} -> {n : _} -> {m : _} -> Vect n elem -> Vect m elem -> Vect (n + m) elem

Lưu ý rằng nó đã không cố gắng điền các kiểu cho các đối số mới, mà thay vào đó đã đưa chúng dưới dạng dấu gạch dưới với hy vọng rằng nó sẽ có thể suy luận chúng từ một số thông tin khác trong phần còn lại của kiểu. Ở đây, điều này dẫn đến kết quả sau:

append : {elem : Type} -> {n : Nat} -> {m : Nat} -> Vect n elem -> Vect m elem -> Vect (n + m) elem

Unbound implicit names

Trên thực tế, Idris sẽ không coi mọi tên không được định nghĩa là một biến ngầm không ràng buộc — chỉ những tên bắt đầu bằng chữ cái thường và xuất hiện một mình hoặc ở vị trí tham số hàm. Cho các trường hợp sau,

test : f m a -> b -> a

m xuất hiện ở vị trí đối số, như a. b xuất hiện một mình, và f chỉ xuất hiện ở vị trí hàm. Do đó, m, a và b được coi là các tham số ẩn không được ràng buộc. f không được coi là một tham số ẩn không được ràng buộc, có nghĩa là nó phải được định nghĩa ở nơi khác để kiểu này là hợp lệ.

Thông thường, để ngắn gọn, bạn để các tham số ngầm hiểu không ràng buộc, nhưng trong một số tình huống, sẽ hữu ích khi sử dụng các tham số ngầm hiểu đã ràng buộc.

For clarity and readability, it can be useful to give explicit types to implicit arguments.
If there’s a dependency between an implicit argument and some other argument, you may need to use a bound implicit to make this clear to Idris.

3.4.3.
Using implicit arguments in functions

Về mặt nội bộ, Idris xử lý các tham số ẩn giống như bất kỳ tham số nào khác, nhưng với sự tiện lợi trong ký hiệu rằng lập trình viên không cần phải cung cấp chúng một cách rõ ràng. Do đó, bạn có thể tham chiếu đến các tham số ẩn bên trong định nghĩa hàm và thậm chí thực hiện phân tích trường hợp trên chúng.

Ví dụ, làm thế nào bạn có thể tìm độ dài của một vector? Bạn có thể làm điều này bằng cách phân chia các trường hợp trên chính vector đó:

length : Vect n elem -> Nat length [] = Z length (x :: xs) = 1 + length xs

Bởi vì độ dài là một phần của kiểu, bạn cũng có thể tham chiếu trực tiếp đến nó:

length : Vect n elem -> Nat length {n} xs = n

Ký hiệu {n} trong một mẫu đưa đối số ngụ ý n vào phạm vi, cho phép bạn sử dụng nó trực tiếp.

Nói chung, bạn có thể cung cấp các giá trị rõ ràng cho các đối số ẩn bằng cách sử dụng ký hiệu {n = giá trị}, trong đó n là tên của một đối số ẩn.

*Append> append {elem = Char} {n = 2} {m = 3} append : Vect 2 Char -> Vect 3 Char -> Vect 5 Char

Ở đây, bạn đã áp dụng một phần hàm append cho các tham số ngầm định của nó, tạo ra một hàm chuyên biệt để nối một vector gồm hai ký tự Char với một vector gồm ba ký tự Char.

Ký hiệu này cũng có thể được sử dụng ở phía bên trái của một định nghĩa để phân tách trường hợp trên một tham số ngầm định. Ví dụ, để thực hiện createEmpties trong phần 3.3.2, bạn có thể đã viết nó trực tiếp bằng cách phân tách trường hợp dựa trên độ dài n sau khi đưa nó vào phạm vi:

createEmpties : Vect n (Vect 0 a) createEmpties {n} = ?createEmpties_rhs

"Nếu bạn chia trường hợp trên n trong Atom, bạn sẽ thấy điều này:"

createEmpties : Vect n (Vect 0 a) createEmpties {n = Z} = ?createEmpties_rhs_1 createEmpties {n = (S k)} = ?createEmpties_rhs_2

Cuối cùng, bạn có thể hoàn thành định nghĩa với một tìm kiếm biểu thức cho cả hai lỗ còn lại:

createEmpties : Vect n (Vect 0 a) createEmpties {n = Z} = [] createEmpties {n = (S k)} = [] :: createEmpties

Lưu ý rằng trong cuộc gọi đệ quy, createEmpties là đủ. Không cần cung cấp một giá trị rõ ràng cho chiều dài vì chỉ có một giá trị (k) sẽ kiểm tra kiểu. Mặt khác, nếu bạn thử ở REPL mà không có giá trị cho chiều dài, Idris sẽ báo lỗi:

*transpose> createEmpties (input):Can't infer argument n to createEmpties, Can't infer argument a to createEmpties

Bạn có thể giải quyết điều này bằng cách cung cấp các giá trị rõ ràng cho n và elem, hoặc đưa ra một kiểu mục tiêu cho biểu thức:

*transpose> createEmpties {a=Int} {n=4} [[], [], [], []] : Vect 4 (Vect 0 Int) *transpose> the (Vect 4 (Vect 0 Int)) createEmpties [[], [], [], []] : Vect 4 (Vect 0 Int)

Type and argument erasure

Bởi vì các tham số ngầm định thường được xử lý giống như bất kỳ tham số nào khác, bạn có thể thắc mắc điều gì xảy ra tại thời điểm chạy. Thông thường, bạn sử dụng các tham số ngầm định để cung cấp kiểu chính xác cho các chương trình, vậy điều này có nghĩa là thông tin kiểu phải được biên dịch và có mặt tại thời điểm chạy không?

Thật may mắn, trình biên dịch Idris nhận thức được vấn đề này. Nó sẽ phân tích một chương trình trước khi biên dịch để đảm bảo rằng bất kỳ tham số nào chỉ được sử dụng để kiểm tra kiểu sẽ không có mặt tại thời gian chạy.

3.5. Summary

Functions in Idris are defined by collections of pattern-matching equations.
Patterns arise from the constructors of a data type.
The Atom text editor provides an interactive editing mode that uses the type to help direct function implementation. Similar modes are available for Emacs and Vim.
Interactive editing commands provide natural tools for following the process of type, define, refine.
Interactive editing provides a command for searching for a valid expression that satisfies the type of a hole.
More-precise types, such as Vect, give more information to the compiler both to help check that a function is correct, and to help constrain expression searches.
Matrices are two-dimensional vectors, with the dimensions encoded in the type. Operations on matrices such as addition and multiplication can be given types that precisely describe how the operations affect the dimensions.
The type-define-refine process helps you to implement matrix operations with precise types by using the type to direct the implementation of each subexpression and create appropriate helper functions.
Type-level variables are implicit arguments to functions, which can be brought into scope and used like any other arguments by enclosing them in braces {}.

Chapter 4.
User-defined data types

Chương này đề cập đến

Defining your own data types
Understanding different forms of data types
Writing larger interactive programs in the type-driven style

Phát triển dựa trên kiểu không chỉ liên quan đến việc gán kiểu chính xác cho các hàm, như bạn đã thấy cho đến nay, mà còn phải suy nghĩ về cách thức dữ liệu được cấu trúc. Theo một cách nào đó, lập trình (đặc biệt là lập trình hàm thuần túy) là về việc biến đổi dữ liệu từ dạng này sang dạng khác. Các kiểu cho phép chúng ta mô tả hình thức của dữ liệu đó, và càng chính xác hơn chúng ta làm những mô tả này, thì ngôn ngữ có thể cung cấp càng nhiều hướng dẫn trong việc thực hiện các biến đổi trên dữ liệu đó.

Nhiều kiểu dữ liệu hữu ích được phân phối như một phần của thư viện Idris, nhiều trong số đó mà chúng ta đã sử dụng cho đến nay, chẳng hạn như List, Bool và Vect. Ngoài việc được định nghĩa trực tiếp trong Idris, không có gì đặc biệt về những kiểu dữ liệu này. Trong bất kỳ chương trình thực tế nào, bạn sẽ cần định nghĩa các kiểu dữ liệu riêng của mình để nắm bắt các yêu cầu cụ thể của vấn đề mà bạn đang giải quyết và các dạng dữ liệu cụ thể mà bạn đang làm việc. Không chỉ vậy, mà việc suy nghĩ cẩn thận về thiết kế các kiểu dữ liệu mang lại lợi ích đáng kể: càng chính xác các kiểu dữ liệu nắm bắt các yêu cầu của một vấn đề, bạn sẽ càng nhận được nhiều lợi ích từ việc chỉnh sửa theo hướng dẫn của kiểu dữ liệu tương tác.

Trong chương này, chúng ta sẽ xem cách định nghĩa các loại dữ liệu mới. Bạn sẽ thấy các hình thức khác nhau của các loại dữ liệu trong một số hàm ví dụ nhỏ. Chúng ta cũng sẽ bắt đầu làm việc với một ví dụ lớn hơn, một kho dữ liệu tương tác, mà chúng ta sẽ mở rộng trong các chương tiếp theo. Ban đầu, chúng ta sẽ chỉ lưu trữ các chuỗi, truy cập chúng bằng chỉ số số nguyên, nhưng ngay cả trong ví dụ nhỏ này, bạn sẽ thấy làm thế nào các loại do người dùng định nghĩa và các loại phụ thuộc có thể giúp xây dựng một giao diện tương tác, xử lý an toàn với các lỗi có thể xảy ra tại runtime.

4.1. Defining data types

Các kiểu dữ liệu được định nghĩa bởi một bộ xây dựng kiểu và một hoặc nhiều bộ xây dựng dữ liệu. Thực ra, bạn đã thấy những điều này khi bạn sử dụng :doc để xem chi tiết về một kiểu dữ liệu. Ví dụ, danh sách dưới đây hiển thị đầu ra của :doc List, được chú thích để làm nổi bật các bộ xây dựng kiểu và dữ liệu.

Listing 4.1.
Type and data constructors from `:doc`

Việc sử dụng các bộ tạo dữ liệu là cách chuẩn để xây dựng các loại được cung cấp bởi bộ tạo loại. Trong trường hợp của List, điều này có nghĩa là mọi giá trị có kiểu dạng List elem đều là Nil hoặc có dạng x :: xs cho một phần tử x và phần còn lại của danh sách, xs.

Chúng tôi sẽ phân loại các loại thành năm nhóm cơ bản, mặc dù chúng đều được định nghĩa với cùng một cú pháp.

Enumerated types— Types defined by giving the possible values directly
Union types— Enumerated types that carry additional data with each value
Recursive types— Union types that are defined in terms of themselves
Generic types— Types that are parameterized over some other types
Dependent types— Types that are computed from some other value

Trong phần này, bạn sẽ thấy cách định nghĩa các kiểu liệt kê, kiểu union, kiểu đệ quy và kiểu tổng quát; chúng ta sẽ bàn về các kiểu phụ thuộc trong phần tiếp theo. Nếu bạn đã lập trình trong một ngôn ngữ hàm trước đây, hoặc trong bất kỳ ngôn ngữ nào cho phép bạn định nghĩa các kiểu tổng quát, thì các kiểu mà chúng ta sẽ thảo luận trong phần này sẽ khá quen thuộc, ngay cả khi ký hiệu là mới.

Naming conventions

Theo quy ước, tôi sẽ sử dụng chữ cái viết hoa cho cả các bộ tạo kiểu và bộ tạo dữ liệu, và chữ cái viết thường cho các hàm. Không có yêu cầu phải làm như vậy, nhưng điều này cung cấp một chỉ dẫn hình ảnh hữu ích cho người đọc mã.

4.1.1.
Enumerations

Một kiểu số đếm được định nghĩa trực tiếp bằng cách đưa ra các giá trị hợp lệ cho kiểu đó. Ví dụ đơn giản nhất là Bool, được định nghĩa như sau trong Prelude:

data Bool = False | True

Để định nghĩa một kiểu dữ liệu liệt kê, bạn sử dụng từ khóa dữ liệu để giới thiệu khai báo, sau đó đưa ra tên của bộ tạo kiểu (trong trường hợp này là Bool) và liệt kê tên của các bộ tạo dữ liệu (trong trường hợp này là True và False).

Hình 4.1 cho thấy một ví dụ khác, định nghĩa một kiểu liệt kê để đại diện cho bốn phương hướng chính trên la bàn.

Figure 4.1.
Defining a `Direction` data type (Direction.idr)

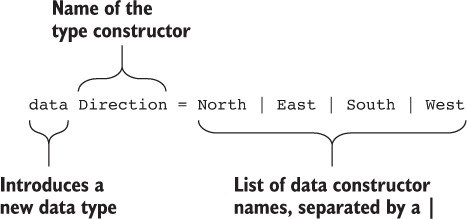
Tên các bộ tạo dữ liệu được phân tách bằng một dấu gạch đứng, |, và không có bất kỳ hạn chế nào về cách bố trí tuyên bố (ngoài quy tắc bố trí thông thường rằng tất cả các tuyên bố phải bắt đầu ở cùng một cột). Ví dụ, chúng có thể nằm ở mỗi dòng khác nhau:

data Direction = North | East | South | West

Một khi bạn đã xác định một kiểu dữ liệu, bạn có thể sử dụng nó để định nghĩa các hàm tương tác. Ví dụ, bạn có thể định nghĩa một hàm turnClockwise như sau, với quy trình thông thường là kiểu, định nghĩa, tinh chỉnh:

Type— Write a function type with Direction as the input and output, and then create a skeleton definition:
```
turnClockwise : Direction -> Direction turnClockwise x = ?turnClockwise_rhs
```

Define— Define the function by case splitting on x:

turnClockwise : Direction -> Direction turnClockwise North = ?turnClockwise_rhs_1 turnClockwise East = ?turnClockwise_rhs_2 turnClockwise South = ?turnClockwise_rhs_3 turnClockwise West = ?turnClockwise_rhs_4

Refine—

Fill in the holes on the right sides:

turnClockwise : Direction -> Direction turnClockwise North = East turnClockwise East = South turnClockwise South = West turnClockwise West = North

4.1.2.
Union types

Một kiểu union là một sự mở rộng của kiểu liệt kê trong đó các nhà xây dựng của kiểu có thể mang dữ liệu. Ví dụ, bạn có thể tạo một kiểu liệt kê cho các hình dạng:

data Shape = Triangle | Rectangle | Circle

Bạn có thể muốn lưu trữ thêm thông tin với một hình dạng, để bạn có thể vẽ nó, chẳng hạn, hoặc tính diện tích của nó. Thông tin này sẽ khác nhau tùy thuộc vào hình dạng:

For a triangle, you might want to know the length of its base and its height.
For a rectangle, you might want to know its length and height.
For a circle, you might want to know its radius.

Để biểu diễn thông tin này, mỗi một cấu trúc dữ liệu, Tam giác, Hình chữ nhật và Hình tròn, có thể được cung cấp các loại đối số mang theo dữ liệu này sử dụng số thực để biểu thị kích thước. Hình 4.2 cho thấy một số hình dạng mẫu và các biểu diễn của chúng.

Figure 4.2.
Example shapes represented as a union type. `Triangle` takes two `Doubles`, for base and height; `Rectangle` takes two `Doubles`, for width and height; `Circle` takes a `Double` for radius.

Bạn có thể biểu diễn các hình dạng dưới dạng kiểu dữ liệu Idris như sau:

data Shape = Triangle Double Double | Rectangle Double Double | Circle Double

Danh sách 4.2 cho thấy cách bạn có thể định nghĩa một hàm diện tích tính diện tích của một hình dạng cho mỗi khả năng này. Như một bài tập, thay vì gõ trực tiếp hàm này, hãy cố gắng xây dựng nó bằng các công cụ chỉnh sửa tương tác trong Atom.

Listing 4.2.
Defining a `Shape` type and calculating its area (Shape.idr)

Nếu bạn kiểm tra tài liệu cho Shape bằng :doc, bạn có thể thấy cách khai báo dữ liệu này chuyển đổi thành kiểu và bộ xây dựng dữ liệu:

*Shape> :doc Shape Data type Main.Shape : Type Constructors: Triangle : Double -> Double -> Shape Rectangle : Double -> Double -> Shape Circle : Double -> Shape

Khi bạn định nghĩa các kiểu dữ liệu mới, cũng là một ý tưởng hay để cung cấp tài liệu sẽ được hiển thị với :doc, sử dụng các chú thích tài liệu. Trong trường hợp này, nó giúp chỉ ra mục đích của từng Double. Các chú thích tài liệu được bố trí trong các khai báo dữ liệu bằng cách đặt chú thích trước mỗi bộ khởi tạo:

||| Represents shapes data Shape = ||| A triangle, with its base length and height Triangle Double Double | ||| A rectangle, with its length and height Rectangle Double Double | ||| A circle, with its radius Circle Double

Điều này được hiển thị như sau với :doc:

*Shape> :doc Shape Data type Main.Shape : Type Represents shapes Constructors: Triangle : Double -> Double -> Shape A triangle, with its base length and height Rectangle : Double -> Double -> Shape A rectangle, with its length and height Circle : Double -> Shape A circle, with its radius

Data type syntax

Có hai hình thức khai báo dữ liệu. Trong một hình thức mà bạn đã thấy, bạn liệt kê các bộ dữ liệu và kiểu của các đối số của chúng:

data Shape = Triangle Double Double | Rectangle Double Double | Circle Double

Cũng có thể định nghĩa kiểu dữ liệu bằng cách chỉ định kiểu và các bộ tạo dữ liệu của chúng trực tiếp, theo dạng như trong tài liệu. Bạn có thể định nghĩa Shape như sau:

data Shape : Type where Triangle : Double -> Double -> Shape Rectangle : Double -> Double -> Shape Circle : Double -> Shape

Điều này giống hệt như tuyên bố trước đó. Trong trường hợp này, nó hơi dài dòng hơn một chút, nhưng cú pháp này thì tổng quát và linh hoạt hơn. Bạn sẽ thấy nhiều hơn về điều này sắp tới khi chúng ta định nghĩa các loại phụ thuộc.

Tôi sẽ sử dụng cả hai cách cú pháp trong suốt cuốn sách. Nói chung, tôi sẽ sử dụng dạng ngắn gọn, trừ khi tôi cần linh hoạt hơn.

4.1.3.
Recursive types

Các kiểu dữ liệu cũng có thể đệ quy, tức là được định nghĩa theo chính chúng. Ví dụ, Nat được định nghĩa đệ quy trong Prelude như sau:

data Nat = Z | S Nat

Prelude cũng định nghĩa các hàm và ký hiệu để cho phép Nat được sử dụng như bất kỳ kiểu số nào khác, vì vậy thay vì viết S (S (S (S Z))), bạn chỉ cần viết 4. Tuy nhiên, trong hình thức nguyên thuỷ, nó được định nghĩa bằng các bộ tạo dữ liệu.

Nat and efficiency

Sẽ là hợp lý khi lo ngại về hiệu suất của Nat vì nó được định nghĩa dựa trên các bộ tạo. Tuy nhiên, không cần phải lo lắng, vì ba lý do sau:

In practice, Nat is primarily used structurally, to describe the size of a data structure such as Vect in its type, so the size of a Nat corresponds to the size of the data structure itself.
When a program is compiled, types are erased, so a Nat that appears at the type level, such as in the length of a Vect, is erased.
Internally, the compiler optimizes the representation of Nat so that it’s really stored as a machine integer.

Bạn có thể sử dụng một kiểu đệ quy để mở rộng ví dụ về Hình dạng từ phần trước để đại diện cho những bức tranh lớn hơn. Chúng tôi sẽ định nghĩa một bức tranh là một trong những điều sau đây:

A primitive shape
A combination of two other pictures
A picture rotated through an angle
A picture translated to a different location

Lưu ý rằng ba trong số này được định nghĩa dựa trên chính các bức tranh. Bạn có thể định nghĩa một loại bức tranh theo mô tả không chính thức trước đó, như được trình bày bên dưới.

Listing 4.3.
Defining a `Picture` type recursively, consisting of `Shape`s and smaller `Picture`s (Picture.idr)

Hình 4.3 cho thấy một ví dụ về loại hình ảnh mà bạn có thể đại diện bằng kiểu dữ liệu này. Đối với mỗi hình dạng nguyên thủy, chúng tôi sẽ coi vị trí của nó là góc trên bên trái của một hộp tưởng tượng bao quanh hình dạng.

Figure 4.3.
An example picture combining three shapes translated to different positions

Chúng ta biết rằng có ba hình ảnh phụ, vì vậy để đại diện điều này trong mã, bạn có thể bắt đầu (định nghĩa) bằng cách sử dụng Combine để kết hợp ba hình ảnh phụ lại với nhau:

testPicture : Picture testPicture = Combine ?pic1 (Combine ?pic2 ?pic3)

Để tiếp tục, bạn biết rằng mỗi hình phụ được dịch đến một vị trí cụ thể, vì vậy bạn có thể điền vào các chi tiết đó (tinh chỉnh), để lại khoảng trống cho các hình dạng nguyên thủy.

testPicture : Picture testPicture = Combine (Translate 5 5 ?rectangle) (Combine (Translate 35 5 ?circle) (Translate 15 25 ?triangle))

Cuối cùng, bạn có thể điền vào (tinh chỉnh) các chi tiết của các hình dạng nguyên thủy riêng lẻ. Một cách để làm điều này là sử dụng Ctrl-Alt-L trong Atom để nâng các lỗ lên cấp độ cao nhất (kiểu), và sau đó điền vào định nghĩa, dẫn đến định nghĩa cuối cùng như sau.

Listing 4.4.
The picture from figure 4.3 represented in code (Picture.idr)

Như thường lệ, bạn viết các hàm trên kiểu dữ liệu Hình ảnh bằng cách phân tách trường hợp. Để viết một hàm tính diện tích của mỗi hình dạng nguyên thủy trong một bức tranh, bạn có thể bắt đầu bằng cách viết một kiểu:

pictureArea : Picture -> Double

Sau đó, tạo một định nghĩa khung và phân chia trường hợp theo đối số của nó. Bạn nên đạt được điều sau:

pictureArea : Picture -> Double pictureArea (Primitive x) = ?pictureArea_rhs_1 pictureArea (Combine x y) = ?pictureArea_rhs_2 pictureArea (Rotate x y) = ?pictureArea_rhs_3 pictureArea (Translate x y z) = ?pictureArea_rhs_4

Điều này đã cho bạn một định nghĩa tổng quát, cho thấy các hình thức mà đầu vào có thể có và để lại khoảng trống ở bên phải.

Các tên của các biến x, y và z, được Idris chọn khi tạo các mẫu cho pictureArea, không đặc biệt mang tính thông tin. Bạn có thể chỉ cho Idris cách chọn tên mặc định tốt hơn bằng cách sử dụng chỉ thị %name:

%name Shape shape, shape1, shape2 %name Picture pic, pic1, pic2

Bây giờ, khi Idris cần chọn một tên biến cho một biến có kiểu Shape, nó sẽ chọn shape theo mặc định, tiếp theo là shape1 nếu shape đã có trong phạm vi, tiếp theo là shape2. Tương tự, nó sẽ chọn pic, pic1 hoặc pic2 cho các biến có kiểu Picture.

Sau khi thêm các chỉ thị %name, việc phân chia trường hợp trên tham số sẽ dẫn đến các mẫu với tên biến thông tin hơn:

pictureArea : Picture -> Double pictureArea (Primitive shape) = ?pictureArea_rhs_1 pictureArea (Combine pic pic1) = ?pictureArea_rhs_2 pictureArea (Rotate x pic) = ?pictureArea_rhs_3 pictureArea (Translate x y pic) = ?pictureArea_rhs_4

Định nghĩa hoàn chỉnh được nêu trong danh sách 4.5. Đối với mỗi Hình ảnh mà bạn gặp trong cấu trúc, bạn gọi đệ quy hàm pictureArea, và khi bạn gặp một Hình dạng, bạn gọi hàm area đã được định nghĩa trước đó.

Listing 4.5.
Calculating the total area of all shapes in a `Picture` (Picture.idr)

Luôn là một ý tưởng hay để kiểm tra định nghĩa kết quả tại REPL.

*Picture> pictureArea testPicture 328.5398163397473 : Double

Infinitely recursive types

Các kiểu dữ liệu đệ quy, giống như các hàm đệ quy, cần ít nhất một trường hợp không đệ quy để có thể hữu ích, vì vậy ít nhất một trong các bộ xây dựng cần có một đối số không đệ quy. Nếu bạn không làm như vậy, bạn sẽ không bao giờ có thể xây dựng một phần tử của kiểu đó. Ví dụ:

data Infinite = Forever Infinite

Tuy nhiên, có thể làm việc với các luồng dữ liệu vô hạn bằng cách sử dụng một kiểu Inf tổng quát, mà chúng ta sẽ khám phá trong chương 11.

4.1.4.
Generic data types

Một kiểu dữ liệu tổng quát là một kiểu được tham số hóa dựa trên một kiểu khác. Giống như các kiểu hàm tổng quát, mà bạn đã thấy trong chương 2, các kiểu dữ liệu tổng quát cho phép bạn nắm bắt các mẫu dữ liệu chung.

Để minh họa nhu cầu của các kiểu dữ liệu tổng quát, hãy xem xét một hàm trả về diện tích của tam giác lớn nhất trong một Bức tranh, như đã được định nghĩa trong phần trước. Ban đầu, bạn có thể viết kiểu sau:

biggestTriangle : Picture -> Double

Nhưng nó nên trả về gì nếu trong hình không có tam giác nào? Bạn có thể trả về một giá trị sentinel nào đó, như kích thước âm, nhưng điều này sẽ đi ngược lại với tinh thần phát triển dựa trên kiểu vì bạn sẽ sử dụng Double để đại diện cho điều gì đó không thực sự là một số. Idris cũng không có giá trị null. Thay vào đó, bạn có thể tinh chỉnh kiểu của biggestTriangle, giới thiệu một kiểu union mới để nắm bắt khả năng rằng không có tam giác nào.

data Biggest = NoTriangle | Size Double biggestTriangle : Picture -> Biggest

Tôi sẽ để định nghĩa của biggestTriangle như một bài tập.

Bạn cũng có thể muốn viết một kiểu dữ liệu đại diện cho khả năng thất bại. Ví dụ, bạn có thể viết một hàm chia an toàn cho Double mà trả về lỗi nếu chia cho zero:

data DivResult = DivByZero | Result Double safeDivide : Double -> Double -> DivResult safeDivide x y = if y == 0 then DivByZero else Result (x / y)

Cả Biggest và DivResult đều có cấu trúc giống nhau! Thay vì định nghĩa nhiều loại cho dạng này, bạn có thể định nghĩa một loại tổng quát duy nhất. Thực tế, loại tổng quát như vậy đã tồn tại trong Prelude, gọi là Maybe. Danh sách sau đây cho thấy định nghĩa của Maybe.

Listing 4.6.
A generic type, `Maybe`, that captures the possibility of failure

Trong một kiểu tổng quát, chúng ta sử dụng các biến kiểu như valtype ở đây để đại diện cho các kiểu cụ thể. Bây giờ bạn có thể định nghĩa safeDivide sử dụng Maybe Double thay vì DivResult, với valtype được khởi tạo với Double:

safeDivide : Double -> Double -> Maybe Double safeDivide x y = if y == 0 then Nothing else Just (x / y)

Definition of List

Chúng tôi đã viết một số hàm với kiểu tổng quát, List, được định nghĩa trong Prelude như sau:

data List elem = Nil | (::) elem (List elem)

Các kiểu dữ liệu tổng quát có thể có nhiều hơn một tham số, như được minh họa trong hình 4.4 cho Either, được định nghĩa trong Prelude và đại diện cho một sự lựa chọn giữa hai kiểu thay thế.

Figure 4.4.
Defining the `Either` data type

Generic types and terminology

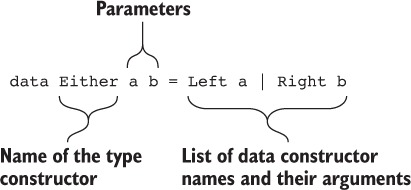
Bạn có thể nghe mọi người không chính thức nói đến “kiểu List” hoặc “kiểu Maybe.” Tuy nhiên, điều này không hoàn toàn chính xác. List tự nó không phải là một kiểu, như bạn có thể xác nhận tại REPL:

Idris> :t List List : Type -> Type

Về mặt kỹ thuật, List có một kiểu hàm mà nhận một Type như một tham số và trả về một Type. Mặc dù List Int là một kiểu vì nó đã được áp dụng cho một tham số cụ thể, nhưng chính List thì không phải. Thay vào đó, chúng ta sẽ không chính thức gọi List là một kiểu tổng quát.

Một ví dụ hữu ích về kiểu tổng quát là cấu trúc cây nhị phân. Danh sách sau đây hiển thị định nghĩa của cây nhị phân, sử dụng chỉ thị %name để cung cấp gợi ý tên cho việc xây dựng các định nghĩa một cách tương tác.

Listing 4.7.
Defining binary trees (Tree.idr)

Cây nhị phân thường được sử dụng để lưu trữ thông tin có thứ tự, trong đó mọi thứ trong cây con bên trái của một nút thì nhỏ hơn giá trị tại nút đó, và mọi thứ trong cây con bên phải của một nút thì lớn hơn giá trị tại nút đó.

Cây như vậy được gọi là cây tìm kiếm nhị phân, và bạn có thể viết một hàm để chèn một giá trị vào cây đó, với điều kiện là bạn có thể sắp xếp những giá trị đó.

insert : Ord elem => elem -> Tree elem -> Tree elem insert x tree = ?insert_rhs

Để viết hàm này, hãy tạo một tệp Tree.idr chứa định nghĩa trong danh sách 4.7 và thực hiện các bước sau:

Define— Case-split on the tree, giving the cases where the tree is Empty and where the tree is a Node:
```
insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = ?insert_rhs_1 insert x (Node tree y tree1) = ?insert_rhs_2
```
Even with the %name directive, the names tree, y, and tree1 aren’t especially informative, so let’s rename them to indicate that they’re the left subtree, the value at the node, and the right subtree, respectively:
```
insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = ?insert_rhs_1 insert x (Node left val right) = ?insert_rhs_2
```

Refine— For ?insert_rhs_1, you create a new tree node with empty subtrees:

insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = Node Empty x Empty insert x (Node left val right) = ?insert_rhs_2

Define— For ?insert_rhs_2, you need to compare the value you’re inserting, x, with the value at the node, val. If x is smaller than val, you insert it into the left subtree. If it’s equal, it’s already in the tree, so you return the tree unchanged. If it’s greater than val, you insert it into the right subtree. To do this, you can use the compare function from the Prelude, which returns an element of an Ordering enumeration:
```
data Ordering = LT | EQ | GT compare : Ord a => a -> a -> Ordering
```
You’ll perform a match on the intermediate result of compare x val. Press Ctrl-Alt-M over insert_rhs_2:
```
insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = Node Empty x Empty insert x (Node left val right) = case _ of case_val => ?insert_rhs_2
```

Define— The case expression won’t type-check until the _ is replaced with an expression to test, so replace it with compare x val:

insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = Node Empty x Empty insert x (Node left val right) = case compare x val of case_val => ?insert_rhs_2

Define— If you now case-split on case_val, you’ll get the patterns for LT, EQ, and GT:

insert : Ord elem => elem -> Tree elem -> Tree elem insert x Empty = Node Empty x Empty insert x (Node left val right) = case compare x val of LT => ?insert_rhs_1 EQ => ?insert_rhs_3 GT => ?insert_rhs_4

Danh sách sau đây hiển thị định nghĩa hoàn chỉnh của hàm này, sau khi hoàn thiện các chỗ trống còn lại.

Listing 4.8.
Inserting a value into a binary search tree (Tree.idr)

@ patterns

Trong phần chèn, bạn có thể đã nhận thấy rằng trong nhánh EQ, giá trị bạn trả về hoàn toàn giống với mẫu ở bên trái. Như một sự tiện lợi về ký hiệu, bạn cũng có thể đặt tên cho các mẫu:

insert x orig@(Node left val right) = case compare x val of LT => Node (insert x left) val right EQ => orig GT => Node left val (insert x right)

Ký hiệu orig@(Node left val right) gán tên orig cho mẫu Node left val right. Nó không làm thay đổi ý nghĩa của việc so khớp mẫu, nhưng có nghĩa là bạn có thể sử dụng tên orig ở phía bên phải thay vì lặp lại mẫu.

Cần có một ràng buộc Ord trên biến tổng quát elem trong kiểu của hàm insert, vì nếu không thì bạn sẽ không thể sử dụng compare. Một cách tiếp cận thay thế là nắm bắt ràng buộc Ord trong chính kiểu cây, làm tinh chỉnh kiểu để bao gồm sự chính xác thêm này. Danh sách sau đây cho thấy cách làm điều này bằng cách chỉ định trực tiếp kiểu và các bộ dữ liệu.

Listing 4.9.
A binary search tree with the ordering constraint in the type (BSTree.idr)

Precision and reuse

Việc đặt một ràng buộc trong cấu trúc cây tự nó làm cho kiểu dữ liệu chính xác hơn, vì bây giờ nó chỉ có thể lưu trữ các giá trị có thể so sánh tại các nút, nhưng đồng thời làm cho nó kém tái sử dụng hơn. Đây là một sự đánh đổi mà bạn sẽ thường phải xem xét khi định nghĩa các kiểu dữ liệu mới. Có nhiều cách để quản lý sự đánh đổi này, chẳng hạn như kết hợp dữ liệu với các tiêu đề mô tả hình thức của dữ liệu đó, như bạn sẽ thấy trong chương 9.

Exercises

Write a function, listToTree : Ord a => List a -> Tree a, that inserts every element of a list into a binary search tree. You can test this at the REPL as follows:
```
*ex_4_1> listToTree [1,4,3,5,2] Node (Node Empty 1 Empty) 2 (Node (Node Empty 3 (Node Empty 4 Empty)) 5 Empty) : Tree Integer
```
Write a corresponding function, treeToList : Tree a -> List a, that flattens a tree into a list using in-order traversal (that is, all the values in the left subtree of a node should be added to the list before the value at the node, which should be added before the values in the right subtree). If you have the correct answers to exercises 1 and 2, you should be able to run this:
```
*ex_4_1> treeToList (listToTree [4,1,8,7,2,3,9,5,6]) [1, 2, 3, 4, 5, 6, 7, 8, 9] : List Integer
```
An integer arithmetic expression can take one of the following forms:
- A single integer
- Addition of an expression to an expression
- Subtraction of an expression from an expression
- Multiplication of an expression with an expression
Define a recursive data type, Expr, that can be used to represent such expressions. Hint: Look at the Picture data type and see how the informal description mapped to the data declaration.
Write a function, evaluate : Expr -> Int, that evaluates an integer arithmetic expression. If you have correct answers to 3 and 4, you should be able to try something like the following at the REPL:
```
*ex_4_1> evaluate (Mult (Val 10) (Add (Val 6) (Val 3))) 90 : Int
```
Write a function, maxMaybe : Ord a => Maybe a -> Maybe a -> Maybe a, that returns the larger of the two inputs, or Nothing if both inputs are Nothing. For example:
```
*ex_4_1> maxMaybe (Just 4) (Just 5) Just 5 : Maybe Integer *ex_4_1> maxMaybe (Just 4) Nothing Just 4 : Maybe Integer
```

Write a function, biggestTriangle : Picture -> Maybe Double, that returns the area of the biggest triangle in a picture, or Nothing if there are no triangles. For example, you can define the following pictures:

testPic1 : Picture testPic1 = Combine (Primitive (Triangle 2 3)) (Primitive (Triangle 2 4)) testPic2 : Picture testPic2 = Combine (Primitive (Rectangle 1 3)) (Primitive (Circle 4))

Then, test biggestTriangle at the REPL as follows:

*ex_4_1> biggestTriangle testPic1 Just 4.0 : Maybe Double *ex_4_1> biggestTriangle testPic2 Nothing : Maybe Double

4.2. Defining dependent data types

Một kiểu dữ liệu phụ thuộc là một kiểu được tính toán từ một giá trị khác. Bạn đã thấy một kiểu phụ thuộc, Vect, nơi kiểu chính xác được tính toán từ độ dài của vector.

Vect : Nat -> Type -> Type

Nói cách khác, loại của Vect phụ thuộc vào độ dài của nó. Điều này mang lại cho chúng ta thêm độ chính xác trong loại, mà chúng tôi đã sử dụng để giúp hướng dẫn lập trình của mình thông qua quá trình loại, định nghĩa, tinh chỉnh. Trong phần này, bạn sẽ thấy cách định nghĩa các loại phụ thuộc như Vect. Cốt lõi của ý tưởng là, vì không có sự phân biệt cú pháp giữa các loại và các biểu thức, các loại có thể được tính toán từ bất kỳ biểu thức nào.

Chúng ta sẽ bắt đầu với một ví dụ đơn giản để minh họa cách thức hoạt động của điều này, định nghĩa một kiểu để đại diện cho các phương tiện và các thuộc tính của chúng, tùy thuộc vào nguồn năng lượng của chúng, và bạn sẽ thấy cách sử dụng điều này để hạn chế các đầu vào hợp lệ cho một hàm chỉ là những cái có ý nghĩa. Bạn sẽ thấy cách định nghĩa Vect cùng với một số phép toán hữu ích trên nó.

4.2.1.
A first example: classifying vehicles by power source

Các loại phụ thuộc cho phép bạn cung cấp thông tin chính xác hơn về các trình tạo dữ liệu của một loại, bằng cách thêm nhiều tham số hơn vào trình tạo loại. Ví dụ, bạn có thể có một kiểu dữ liệu để đại diện cho các phương tiện (chẳng hạn như xe đạp, ô tô và xe buýt), nhưng một số phép toán không có ý nghĩa trên tất cả các giá trị trong loại (chẳng hạn như tiếp nhiên liệu cho xe đạp sẽ không hoạt động vì không có bình nhiên liệu). Do đó, chúng tôi sẽ phân loại các phương tiện thành những phương tiện chạy bằng bàn đạp và những phương tiện chạy bằng xăng, và diễn đạt điều này trong kiểu dữ liệu.

Danh sách dưới đây cho thấy cách bạn có thể diễn đạt điều này trong Idris.

Listing 4.10.
Defining a dependent type for vehicles, with their power source in the type (vehicle.idr)

Bạn có thể viết các hàm sẽ hoạt động trên tất cả các phương tiện bằng cách sử dụng một biến kiểu để đại diện cho nguồn năng lượng. Chẳng hạn, tất cả các phương tiện đều có một số bánh xe. Ngược lại, không phải tất cả các phương tiện đều mang nhiên liệu, vì vậy chỉ có ý nghĩa khi tiếp nhiên liệu cho một phương tiện có loại biểu thị nó được cung cấp năng lượng bằng xăng. Cả hai khái niệm này đều được minh họa trong danh sách dưới đây.

Listing 4.11.
Reading and updating properties of `Vehicle`

Asserting that inputs are impossible

Nếu bạn cố gắng thêm một trường hợp để nạp nhiên liệu cho một chiếc Xe đạp, Idris sẽ báo lỗi kiểu, vì kiểu đầu vào bị giới hạn cho các phương tiện được chạy bằng xăng. Nếu bạn sử dụng các công cụ tương tác, Idris thậm chí sẽ không đưa ra trường hợp cho Xe đạp sau khi thực hiện chia trường hợp với Ctrl-Alt-C. Tuy nhiên, đôi khi nó có thể giúp cải thiện khả năng đọc nếu bạn làm rõ rằng bạn biết trường hợp Xe đạp là không thể. Bạn có thể viết như sau:

refuel : Vehicle Petrol -> Vehicle Petrol refuel (Car fuel) = Car 100 refuel (Bus fuel) = Bus 200 refuel Bicycle impossible

Nếu bạn làm điều này, Idris sẽ kiểm tra rằng trường hợp bạn đã đánh dấu là không thể xảy ra sẽ gây ra lỗi kiểu.

Tương tự, nếu bạn khẳng định một trường hợp là không thể nhưng Idris tin rằng nó hợp lệ, nó sẽ báo lỗi:

refuel : Vehicle Petrol -> Vehicle Petrol refuel (Car fuel) = Car 100 refuel (Bus fuel) impossible

Ở đây, Idris sẽ báo cáo những điều sau:

vehicle.idr:15:8:refuel (Bus fuel) is a valid case

Nói chung, bạn nên định nghĩa các kiểu phụ thuộc bằng cách cung cấp trực tiếp bộ tạo kiểu và các bộ tạo dữ liệu. Điều này mang lại cho bạn rất nhiều sự linh hoạt trong hình thức mà các bộ tạo có thể có. Ở đây, nó đã cho phép bạn định nghĩa các kiểu mà các bộ tạo dữ liệu có thể nhận các đối số khác nhau. Bạn có thể viết các hàm hoạt động trên tất cả các phương tiện (như bánh xe) hoặc các hàm chỉ hoạt động trên một tập hợp con nào đó của các phương tiện (như đổ xăng).

Defining families of types

Đối với Xe cộ, bạn thực sự đã định nghĩa hai loại trong một khai báo (cụ thể là Xe đạp và Xe xăng). Các kiểu dữ liệu phụ thuộc như Xe cộ do đó đôi khi được gọi là các gia đình kiểu, vì bạn đang định nghĩa nhiều kiểu liên quan cùng một lúc. Nguồn năng lượng là một chỉ số của gia đình Xe cộ. Chỉ số cho bạn biết chính xác loại Xe cộ mà bạn đang nói đến.

4.2.2.
Defining vectors

Trong chương 3, chúng ta đã xem xét những cách mà chúng ta có thể sử dụng thông tin chiều dài trong kiểu để giúp thúc đẩy việc phát triển các hàm trên vectơ. Trong phần này, chúng ta sẽ xem xét cách định nghĩa Vect, cùng với một số phép toán trên nó.

Nó được định nghĩa trong module Data.Vect, như được chỉ ra trong danh sách 4.12. Bộ xây dựng kiểu, Vect, nhận một độ dài và một kiểu phần tử làm tham số, vì vậy khi bạn định nghĩa các bộ dữ liệu, bạn nêu rõ trong loại của chúng độ dài là gì.

Listing 4.12.
Defining vectors (Vect.idr)

Thư viện Data.Vect bao gồm một số hàm tiện ích trên Vect, bao gồm nối, tra cứu giá trị theo vị trí của chúng trong vector, và các hàm bậc cao khác, chẳng hạn như map. Tuy nhiên, thay vì nhập khẩu thư viện này, chúng ta sẽ sử dụng định nghĩa riêng của mình về Vect và thử viết một số hàm bằng tay. Để bắt đầu, hãy tạo một tệp Vect.idr chỉ chứa định nghĩa của Vect trong danh sách 4.12.

Bởi vì Vect bao gồm chiều dài một cách rõ ràng trong kiểu của nó, bất kỳ hàm nào sử dụng một thể hiện nào đó của Vect sẽ mô tả các thuộc tính chiều dài của nó một cách rõ ràng trong kiểu của nó. Ví dụ, nếu bạn định nghĩa một hàm nối trên Vect, kiểu của nó sẽ thể hiện cách các chiều dài của các đầu vào và đầu ra liên quan đến nhau.

append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Type-level expressions

Biểu thức n + m trong kiểu trả về ở đây là một biểu thức thông thường với loại Nat, sử dụng toán tử + thông thường. Bởi vì tham số đầu tiên của Vect có loại Nat, bạn nên mong đợi có thể sử dụng bất kỳ biểu thức nào có loại Nat. Hãy nhớ rằng, kiểu là hạng nhất, vì vậy kiểu và biểu thức đều là một phần của cùng một ngôn ngữ.

Sau khi đã viết kiểu đầu tiên, như mọi khi, bạn có thể định nghĩa hàm append bằng cách phân tách trường hợp theo tham số đầu tiên. Bạn thực hiện điều này một cách tương tác như sau:

Define— Begin by creating a skeleton definition and then case splitting on the first argument xs:

append : Vect n elem -> Vect m elem -> Vect (n + m) elem append [] ys = ?append_rhs_1 append (x :: xs) ys = ?append_rhs_2

Refine— Idris has enough information in the type to complete this definition by an expression search on each of the holes, resulting in this:
```
append : Vect n elem -> Vect m elem -> Vect (n + m) elem append [] ys = ys append (x :: xs) ys = x :: append xs ys
```

Terminology: parameters and indices

Vect xác định một họ các kiểu, và chúng tôi nói rằng một Vect được chỉ mục theo độ dài và tham số hóa bởi một kiểu phần tử. Sự phân biệt giữa tham số và chỉ mục như sau:

A parameter is unchanged across the entire structure. In this case, every element of the vector has the same type.
An index may change across a structure. In this case, every subvector has a different length.

Sự phân biệt này rất hữu ích khi xem xét loại của một hàm: bạn có thể chắc chắn rằng giá trị cụ thể của một tham số không thể tham gia vào định nghĩa của hàm. Tuy nhiên, chỉ số có thể, như bạn đã thấy trong chương 3 khi định nghĩa độ dài cho các vector bằng cách xem xét chỉ số độ dài, và khi định nghĩa createEmpties để xây dựng một vector chứa các vector rỗng.

Một phép toán phổ biến khác trên các vector là zip, kết hợp các phần tử tương ứng trong hai vector, như được minh họa trong hình 4.5.

Figure 4.5.
Pairing corresponding elements of `[1,2,3,4]` and `["one","two","three","four"]` using `zip`

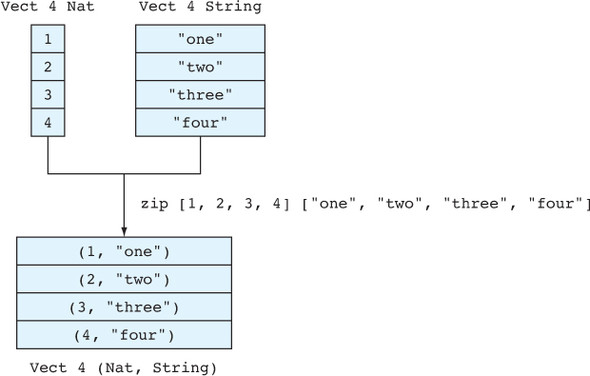
Tên zip được nhằm gợi ý đến cách hoạt động của một khóa kéo, kết nối hai bên của một chiếc túi hoặc áo khoác lại với nhau. Vì độ dài của mỗi Vect đầu vào nằm trong kiểu, bạn cần suy nghĩ về cách độ dài của các đầu vào và đầu ra sẽ tương ứng như thế nào. Một lựa chọn hợp lý cho điều này là yêu cầu độ dài của cả hai đầu vào phải giống nhau.

zip : Vect n a -> Vect n b -> Vect n (a, b)

Việc có một kiểu chính xác hơn cho Vect, nắm bắt độ dài trong kiểu, có nghĩa là bạn cần phải quyết định trước cách mà độ dài của các đầu vào cho hàm zip liên quan đến nhau và thể hiện quyết định này trong kiểu. Ngoài ra, điều này có nghĩa là bạn có thể yên tâm rằng hàm zip chỉ bao giờ được gọi với các danh sách có độ dài bằng nhau, vì nếu giả định này bị vi phạm, Idris sẽ báo lỗi kiểu.

Bạn có thể định nghĩa zip, như thường lệ, từng bước một:

Define— Again, you can begin to define this by a case split on the first argument:

zip : Vect n a -> Vect n b -> Vect n (a, b) zip [] ys = ?zip_rhs_1 zip (x :: xs) ys = ?zip_rhs_2

Refine— You can fill in ?zip_rhs_1 with an expression search, because the only well-typed result is an empty vector:
```
zip : Vect n a -> Vect n b -> Vect n (a, b) zip [] ys = [] zip (x :: xs) ys = ?zip_rhs_2
```
Refine— For the second case, ?zip_rhs_2, take a look at the type of the hole and see if that gives you further information about what to do:
```
 b : Type a : Type x : a k : Nat xs : Vect k a ys : Vect (S k) b -------------------------------------- zip_rhs_2 : Vect (S k) (a, b)
```
Notice that ys has length S k, meaning that there must be at least one element. If you case-split on ys, Idris won’t give you a pattern for the empty list, because it wouldn’t be a well-typed value:
```
zip : Vect n a -> Vect n b -> Vect n (a, b) zip [] ys = [] zip (x :: xs) (y :: ys) = ?zip_rhs_1
```
After the case split, Idris has created a new hole, so let’s take a look at the types of the local variables:
```
 b : Type a : Type x : a k : Nat xs : Vect k a y : b ys : Vect k b -------------------------------------- zip_rhs_1 : Vect (S k) (a, b)
```
Again, there’s enough information to complete the definition with an expression search:
```
zip : Vect n a -> Vect n b -> Vect n (a, b) zip [] ys = [] zip (x :: xs) (y :: ys) = (x, y) :: zip xs ys
```
Idris has noticed that it needs to build a vector of length S k, that it can create the appropriate vector of length k with a recursive call, and that it can create the appropriate first element by pairing x and y.

Deconstructing expression searches

Để hiểu những gì tìm kiếm biểu thức đã thực hiện, có thể hữu ích để loại bỏ một phần của kết quả và thay thế nó bằng một khoảng trống, để xem loại biểu thức nào mà việc tìm kiếm đang làm việc tại thời điểm đó. Ví dụ, bạn có thể loại bỏ phần (x, y):

zip : Vect n a -> Vect n b -> Vect n (a, b) zip [] ys = [] zip (x :: xs) (y :: ys) = ?element :: zip xs ys

Sau đó, kiểm tra loại của phần tử ?hole, bạn sẽ thấy rằng vào thời điểm này, Idris đang tìm kiếm một cặp a và b:

 b : Type a : Type x : a k : Nat xs : Vect k a y : b ys : Vect k b -------------------------------------- element : (a, b)

Cách duy nhất để tạo ra một cặp a và b vào thời điểm này là sử dụng x và y, vì vậy đây là những gì Idris đã sử dụng để xây dựng cặp này.

4.2.3.
Indexing vectors with bounded numbers using Fin

Bởi vì Vect mang chiều dài của chúng như một phần của kiểu dữ liệu, trình kiểm tra loại có thêm thông tin mà nó có thể sử dụng để kiểm tra rằng các thao tác được thực hiện và sử dụng đúng cách. Một ví dụ là nếu bạn muốn tìm một phần tử trong một Vect theo vị trí của nó trong vector, bạn có thể biết tại thời điểm biên dịch rằng vị trí đó sẽ không thể vượt quá giới hạn khi chương trình được chạy.

Hàm chỉ mục, được định nghĩa trong Data.Vect, là một hàm tra cứu an toàn biên có kiểu bảo đảm rằng nó sẽ không bao giờ truy cập vào một vị trí nằm ngoài giới hạn của một vectơ.

index : Fin n -> Vect n a -> a

Tham số đầu tiên, loại Fin n, là một số không âm có giới hạn trên không bao gồm n. Tên gọi Fin gợi ý rằng số này có giới hạn hữu hạn. Vì vậy, ví dụ, khi bạn tra cứu một phần tử theo vị trí, bạn có thể sử dụng một số trong phạm vi của vector:

Idris> :module Data.Vect *Data/Vect> Vect.index 3 [1,2,3,4,5]

Importing modules at the REPL

Trong ví dụ tìm kiếm phần tử, bạn nhập Data.Vect tại REPL bằng lệnh :module để truy cập vào hàm index. Có một số hàm trong Prelude được gọi là index để lập chỉ mục cho các cấu trúc giống danh sách khác nhau, vì vậy bạn phải làm rõ một cách rõ ràng với Vect.index ở đây.

Nhưng nếu bạn cố gắng sử dụng một số nằm ngoài giới hạn, bạn sẽ nhận được lỗi kiểu.

*Data/Vect> Vect.index 7 [1,2,3,4,5] (input):1:14:When checking argument prf to function Data.Fin.fromInteger: When using 7 as a literal for a Fin 5 7 is not strictly less than 5

Integer literal notation

Giống như với Nat, bạn có thể sử dụng hằng số số nguyên cho Fin, với điều kiện là trình biên dịch có thể chắc chắn rằng hằng số đó nằm trong các giới hạn được nêu trong kiểu dữ liệu.

Nếu bạn đang đọc một số từ đầu vào của người dùng mà sẽ được sử dụng để lập chỉ mục cho một Vect, số đó sẽ không phải lúc nào cũng nằm trong giới hạn của Vect. Thực tế, bạn thường cần phải chuyển đổi từ một số nguyên có kích thước tùy ý sang một Fin có giới hạn.

Nhập Data.Vect cung cấp cho bạn quyền truy cập vào hàm integerToFin, hàm này chuyển đổi một Integer thành một Fin với một số giới hạn, miễn là Integer nằm trong giới hạn. Nó có kiểu sau:

integerToFin : Integer -> (n : Nat) -> Maybe (Fin n)

Tham số đầu tiên là số nguyên cần chuyển đổi, và tham số thứ hai là giới hạn trên của Fin. Hãy nhớ rằng một kiểu Fin upper, với một giá trị của upper, đại diện cho các số đến nhưng không bao gồm upper, vì vậy 5 không phải là một Fin 5 hợp lệ, nhưng 4 thì có. Dưới đây là một vài ví dụ:

*Data/Vect> integerToFin 2 5 Just (FS (FS FZ)) : Maybe (Fin 5) *Data/Vect> integerToFin 6 5 Nothing : Maybe (Fin 5)

Fin constructors

FZ và FS là các trình tạo của Fin, tương ứng với Z và S như các trình tạo của Nat. Thông thường, bạn có thể sử dụng các số nguyên, giống như với Nat.

Sử dụng integerToFin, bạn có thể viết một hàm tryIndex để tra cứu một giá trị trong Vect bằng chỉ số Integer, sử dụng Maybe trong kiểu để nắm bắt khả năng rằng kết quả có thể vượt quá phạm vi. Bắt đầu bằng cách tạo một tệp TryIndex.idr nhập khẩu Data.Vect. Sau đó, thực hiện theo các bước sau:

Type— As ever, start by giving a type:
```
tryIndex : Integer -> Vect n a -> Maybe a
```
Note that this type gives no relationship between the input Integer and the length of the Vect.
Define— You can write the definition by using integerToFin to check whether the input is within range:
```
tryIndex : Integer -> Vect n a -> Maybe a tryIndex {n} i xs = case integerToFin i n of case_val => ?tryIndex_rhs
```
Note that you need to bring n into scope so that you can pass it to integerToFin as the desired bound of the Fin.
Define— Now, define the function by case splitting on case_val. If integerToFin returns Nothing, the input was out of bounds, so you return Nothing:
```
tryIndex : Integer -> Vect n a -> Maybe a tryIndex {n} i xs = case integerToFin i n of Nothing => Nothing Just idx => ?tryIndex_rhs_2
```
Type— If you inspect the type of tryIndex_rhs_2, you’ll see that you now have a Fin n and a Vect n a, so you can safely use index:
```
 n : Nat idx : Fin n a : Type i : Integer xs : Vect n a -------------------------------------- tryIndex_rhs_2 : Maybe a
```

Kết quả cuối cùng như sau:

tryIndex : Integer -> Vect n a -> Maybe a tryIndex {n} i xs = case integerToFin i n of Nothing => Nothing Just idx => Just (index idx xs)

Đây là một mẫu phổ biến trong lập trình kiểu phụ thuộc, mà bạn sẽ thấy thường xuyên hơn trong các chương tiếp theo. Kiểu của chỉ số cho bạn biết khi nào thì an toàn để gọi nó, vì vậy nếu bạn có một đầu vào có thể không an toàn, bạn cần phải kiểm tra. Khi bạn đã chuyển đổi Integer thành Fin n, bạn biết rằng số đó phải nằm trong giới hạn, vì vậy bạn không cần phải kiểm tra lại.

Exercises

Extend the Vehicle data type so that it supports unicycles and motorcycles, and update wheels and refuel accordingly.
Extend the PowerSource and Vehicle data types to support electric vehicles (such as trams or electric cars).
The take function, on List, has type Nat -> List a -> List a. What’s an appropriate type for the corresponding vectTake function on Vect? Hint: How do the lengths of the input and output relate? It shouldn’t be valid to take more elements than there are in the Vect. Also, remember that you can have any expression in a type.

Implement vectTake. If you’ve implemented it correctly, with the correct type, you can test your answer at the REPL as follows:

*ex_4_2> vectTake 3 [1,2,3,4,5,6,7] [1, 2, 3] : Vect 3 Integer

You should also get a type error if you try to take too many elements:

*ex_4_2> vectTake 8 [1,2,3,4,5,6,7] (input):1:14:When checking argument xs to constructor Main.::: Type mismatch between Vect 0 a1 (Type of []) and Vect (S m) a (Expected type)

Write a sumEntries function with the following type:
```
sumEntries : Num a => (pos : Integer) -> Vect n a -> Vect n a -> Maybe a
```
It should return the sum of the entries at position pos in each of the inputs if pos is within bounds, or Nothing otherwise. For example:
```
*ex_4_2> sumEntries 2 [1,2,3,4] [5,6,7,8] Just 10 : Maybe Integer *ex_4_2> sumEntries 4 [1,2,3,4] [5,6,7,8] Nothing : Maybe Integer
```
Hint: You’ll need to call integerToFin, but you’ll only need to do it once.

4.3. Type-driven implementation of an interactive data store

Để đưa những ý tưởng mà bạn đã học được vào thực tiễn, hãy cùng xem xét một ví dụ chương trình lớn hơn, một kho dữ liệu tương tác. Trong phần này, chúng ta sẽ thiết lập cơ sở hạ tầng cơ bản. Chúng ta sẽ xem xét lại chương trình này trong chương 6, khi bạn học thêm về Idris, để hỗ trợ các cặp khóa-giá trị, với các sơ đồ mô tả hình thức của dữ liệu.

Trong triển khai ban đầu của chúng tôi, chúng tôi chỉ hỗ trợ lưu trữ dữ liệu dưới dạng Chuỗi, trong bộ nhớ, được truy cập bằng một định danh số. Nó sẽ có một dòng lệnh và hỗ trợ các lệnh sau:

add [String] adds a string to the document store and responds by printing an identifier by which you can refer to the string.
get [Identifier] retrieves and prints the string with the given identifier, assuming the identifier exists, or an error message otherwise.
quit exits the program.

Một phiên ngắn có thể diễn ra như sau:

$ ./datastore Command: add Even Old New York ID 0 Command: add Was Once New Amsterdam ID 1 Command: get 1 Was Once New Amsterdam Command: get 2 Out of range Command: add Why They Changed It I Can't Say ID 2 Command: get 2 Why They Changed It I Can't Say Command: quit

Chúng ta sẽ sử dụng hệ thống kiểu để đảm bảo rằng tất cả các truy cập vào kho dữ liệu đều sử dụng các định danh hợp lệ, và tất cả các hàm của chúng ta sẽ là tổng quát để chúng ta chắc chắn rằng chương trình sẽ không bị ngắt do đầu vào không mong đợi.

Cách tiếp cận tổng thể mà chúng tôi sẽ thực hiện, ở mức độ cao, lại tuân theo quy trình loại, định nghĩa, tinh chỉnh:

Type— Design a new data type for the representation of the data store. In type-driven development, even at the highest level, types come first. Before we can implement any part of a data store program, we need to know how we’re representing and working with the data.
Define— Implement as much of a main program as we can, leaving holes for parts we can’t write immediately, lifting these holes to top-level functions.
Refine— As we go deeper into the implementation and improve our understanding of the problem, we’ll refine the implementation and types as necessary.

Để bắt đầu, hãy tạo một phác thảo của file DataStore.idr chứa một tiêu đề module, một câu lệnh nhập cho Data.Vect và một hàm main trống, như sau.

Listing 4.13.
Outline implementation of the data store (DataStore.idr)

Chúng ta sẽ bắt đầu bằng cách định nghĩa một kiểu để đại diện cho cửa hàng, sau đó chúng ta sẽ viết một hàm chính để đọc dữ liệu đầu vào từ người dùng và cập nhật cửa hàng theo các lệnh của người dùng. Khi chúng ta tiến hành thực hiện, chúng ta sẽ thêm các kiểu và hàm mới khi cần thiết, luôn được hướng dẫn bởi bộ kiểm tra kiểu của Idris.

4.3.1.
Representing the store

Kho dữ liệu tự nó, ban đầu, là một tập hợp các chuỗi. Chúng ta sẽ bắt đầu bằng cách định nghĩa một kiểu cho kho, bao gồm kích thước của kho (tức là số lượng món đồ đã lưu), một cách rõ ràng và sử dụng Vect cho các món đồ, như được trình bày trong danh sách sau. Bạn có thể thêm điều này vào DataStore.idr, trên định nghĩa rỗng ban đầu của main.

Listing 4.14.
A data type for representing the data store (DataStore.idr)

Bạn có thể truy cập kích thước và nội dung của một kho dữ liệu bằng cách viết các hàm mẫu kết hợp với kho dữ liệu và trích xuất các trường thích hợp. Những điều này được hiển thị trong danh sách sau.

Listing 4.15.
Projecting out the size and content of a data store (DataStore.idr)

Trong danh sách này, độ dài của Vect trong loại mặt hàng được tính toán bởi một hàm, size.

Records

Một kiểu dữ liệu có một bộ dựng như DataStore về cơ bản là một bản ghi với các trường cho dữ liệu của nó. Trong chương 6, bạn sẽ thấy một cú pháp ngắn gọn hơn cho các bản ghi, giúp tránh việc phải viết các hàm chiếu rõ ràng như size và items.

Bạn cũng cần thêm các mục dữ liệu mới vào cửa hàng, như trong danh sách 4.16. Điều này sẽ thêm các mục vào cuối cửa hàng, thay vì tại đầu bằng cách sử dụng :: trực tiếp. Lý do cho điều này là vì chúng tôi dự định truy cập các mục theo chỉ số nguyên của chúng; nếu bạn thêm các mục ở đầu, thì các mục mới sẽ luôn có chỉ số là không, và mọi thứ khác sẽ bị dịch chuyển sang một vị trí.

Listing 4.16.
Adding a new entry to the data store (DataStore.idr)

Interactive editing in where blocks

Các công cụ chỉnh sửa tương tác hoạt động hiệu quả giống như ở cấp độ cao nhất. Ví dụ, hãy thử triển khai addToStore bắt đầu từ điểm này:

addToStore : DataStore -> String -> DataStore addToStore (MkData size items) newitem = MkData _ (addToData items) where addToData : Vect old String -> Vect (S old) String

Bạn có thể sử dụng Ctrl-Alt-A để thêm một định nghĩa cho addToData, và tìm kiếm biểu thức với Ctrl-Alt-S nhận biết rằng newitem nằm trong phạm vi.

4.3.2.
Interactively maintaining state in main

Khi bạn triển khai hàm chính cho kho dữ liệu của mình, bạn sẽ cần đọc đầu vào từ người dùng, duy trì trạng thái của kho dữ liệu và cho phép người dùng thoát. Trong chương trước, chúng ta đã sử dụng hàm Prelude repl để viết một chương trình tương tác đơn giản mà liên tục đọc đầu vào, thực hiện một hàm trên đó và hiển thị kết quả.

repl : String -> (String -> String) -> IO ()

Rất tiếc, điều này chỉ cho phép những tương tác đơn giản lặp đi lặp lại mãi mãi.

Đối với các chương trình phức tạp hơn giữ trạng thái, Prelude cung cấp một hàm khác, replWith, thực hiện một vòng lặp đọc-đánh giá-in mà mang theo một số trạng thái. :doc mô tả nó như sau:

Idris> :doc replWith Prelude.Interactive.replWith : (state : a) -> (prompt : String) -> (onInput : a -> String -> Maybe (String, a)) -> IO () A basic read-eval-print loop, maintaining a state Arguments: state : a -- the input state prompt : String -- the prompt to show onInput : a -> String -> Maybe (String, a) -- the function to run on reading input, returning a String to output and a new state. Returns Nothing if the repl should exit

Trên mỗi lần lặp qua vòng lặp, nó gọi đối số onInput, mà chính nó nhận hai đối số:

The current state, of some generic type a
The String entered at the prompt

Giá trị mà hàm onInput cần trả về có kiểu Maybe (String, a), có nghĩa là nó có thể ở một trong các dạng sau:

Nothing, if it wants the loop to exit
Just (output, newState), if it wants to print some output and update the state to newState for the next iteration

Bảng liệt kê tiếp theo cho thấy một ví dụ đơn giản về điều này đang hoạt động: một chương trình tương tác đọc một số nguyên từ bảng điều khiển và hiển thị tổng của các đầu vào. Nếu nó đọc một giá trị âm, nó sẽ thoát.

Listing 4.17.
Interactive program to sum input values until a negative value is read (SumInputs.idr)

Bạn có thể sử dụng replWith để tinh chỉnh hàm chính trong kho dữ liệu. Ở giai đoạn này bạn có

A type for the data store (DataStore)
A way of accessing the items in the store (items)
A way of updating the store with new items (addToStore)

Khi bạn gọi replWith, bạn cần truyền dữ liệu ban đầu, một thông điệp, và một hàm để xử lý đầu vào như các đối số. Bạn có thể truyền một kho dữ liệu trống đã được khởi tạo và một chuỗi thông điệp, nhưng bạn vẫn chưa có một hàm để xử lý đầu vào của người dùng. Tuy nhiên, bạn có thể tinh chỉnh định nghĩa của hàm chính thành dạng sau, để lại một khoảng trống cho hàm xử lý đầu vào:

main : IO () main = replWith (MkData _ []) "Command: " ?processInput

Quá trình nâng cao đầu vào cho biết loại bạn phải làm việc với:

processInput : DataStore -> String -> Maybe (String, DataStore) main : IO () main = replWith (MkData _ []) "Command: " processInput

Theo cách tiếp cận dựa trên kiểu, khi bạn tinh chỉnh định nghĩa của hàm main với một ứng dụng của replWith, Idris đã có thể xác định kiểu chuyên biệt cần thiết cho processInput.

4.3.3.
Commands: parsing user input

Để xử lý chuỗi đầu vào, bạn cần phải tìm ra lệnh nào trong các lệnh add, get hoặc quit đã được nhập. Thay vì xử lý trực tiếp chuỗi đầu vào, thường thì việc định nghĩa một kiểu dữ liệu mới đại diện cho các lệnh có thể là cách làm sạch hơn. Bằng cách này, bạn có thể tách biệt một cách rõ ràng việc phân tích các lệnh với việc xử lý chúng.

Do đó, bạn sẽ định nghĩa một kiểu dữ liệu Command, là một kiểu union đại diện cho các lệnh có thể và các tham số của chúng. Đặt định nghĩa sau vào DataStore.idr trên processInput:

data Command = Add String | Get Integer | Quit

Avoid using strings for data representation

Người dùng nhập một Chuỗi, nhưng chỉ một số lượng nhất định của các Chuỗi là lệnh đầu vào hợp lệ. Việc giới thiệu loại Lệnh làm cho việc biểu diễn các lệnh chính xác hơn vì chỉ những lệnh hợp lệ mới có thể được biểu diễn. Nếu người dùng nhập một Chuỗi không thể chuyển đổi thành một Lệnh, thì các loại buộc bạn phải suy nghĩ về cách xử lý lỗi. Ban đầu, bạn có thể để lại một khoảng trống trong chương trình để xử lý lỗi, nhưng cuối cùng, việc tạo ra một loại chính xác dẫn đến một triển khai mạnh mẽ hơn.

Bạn cần chuyển đổi chuỗi được nhập bởi người dùng thành một Lệnh. Tuy nhiên, đầu vào có thể không hợp lệ, vì vậy loại hàm để phân tích lệnh sẽ phản ánh khả năng này trong kiểu của nó:

parse : (input : String) -> Maybe Command

Bạn có thể viết một trình phân tích cú pháp đơn giản cho các lệnh đầu vào bằng cách tìm khoảng trắng đầu tiên trong đầu vào sử dụng hàm span để xác định phần nào của đầu vào là lệnh và phần nào là đối số. Hàm span hoạt động như sau:

Idris> :t Strings.span span : (Char -> Bool) -> String -> (String, String) Idris> span (/= ' ') "Hello world, here is a string" ("Hello", " world, here is a string") : (String, String)

Giá trị đầu tiên, (/= ' '), là một phép kiểm tra trả về một giá trị Bool. Phép kiểm tra này trả về True cho bất kỳ ký tự nào không bằng một khoảng trống. Giá trị thứ hai là một chuỗi đầu vào, và hàm span sẽ chia chuỗi thành hai phần:

The first part is the prefix of the input string, where all characters satisfy the test.
The second part is the remainder of the string. If all characters in the string satisfy the test, this will be empty.

Bạn có thể định nghĩa phân tích với Ctrl-Alt-A và sau đó tinh chỉnh định nghĩa của nó như sau:

parse : (input : String) -> Maybe Command parse input = case span (/= ' ') input of (cmd, args) => ?parseCommand

Bạn có thể nâng parseCommand lên thành một hàm cấp cao với kiểu thích hợp, sử dụng Ctrl-Alt-L:

parseCommand : (cmd : String) -> (args : String) -> (input : String) -> Maybe Command parse : (input : String) -> Maybe Command parse input = case span (/= ' ') input of (cmd, args) => parseCommand cmd args input

Bạn sẽ không cần tham số đầu vào vì bạn sẽ phân tích đầu vào từ cmd và args một mình, mặc dù Idris đã thêm nó vì đầu vào nằm trong phạm vi. Do đó, bạn có thể chỉnh sửa kiểu:

parseCommand : (cmd : String) -> (args : String) -> Maybe Command parse : (input : String) -> Maybe Command parse input = case span (/= ' ') input of (cmd, args) => parseCommand cmd args

Ngoài ra, bạn có thể thấy rằng args, nếu không rỗng, sẽ có một khoảng cách ở đầu, vì ký tự đầu tiên mà span gặp phải không thỏa mãn điều kiện sẽ là một khoảng trắng. Bạn có thể loại bỏ các khoảng trắng ở đầu bằng hàm ltrim : String -> String, hàm này trả về đầu vào của nó với các ký tự trắng ở đầu bị loại bỏ:

parseCommand : (cmd : String) -> (args : String) -> Maybe Command parse : (input : String) -> Maybe Command parse input = case span (/= ' ') input of (cmd, args) => parseCommand cmd (ltrim args)

Bạn bây giờ có thể viết hàm parseCommand bằng cách kiểm tra các đối số cmd và args. Bạn sẽ cần một số hàm trong Prelude để hoàn thành định nghĩa của parseCommand:

unpack : String -> List Char converts a String into a list of characters.
isDigit : Char -> Bool returns whether a Char is one of the digits 0–9.
all : (a -> Bool) -> List a -> Bool returns whether every entry in a list satisfies a test.

Vì vậy, biểu thức all isDigit (unpack val) sẽ trả về xem chuỗi val hoàn toàn bao gồm các chữ số hay không.

Documentation and Prelude functions

Nói chung, hãy nhớ rằng bạn có thể sử dụng :doc tại REPL, hoặc Ctrl-Alt-D trong Atom, để kiểm tra tài liệu cho bất kỳ tên nào, cho dù chúng là các trình xây dựng kiểu, trình xây dựng dữ liệu hay hàm.

Danh sách 4.18 cho thấy cách phân tích cú pháp đầu vào hoạt động. Đặc biệt, hãy lưu ý rằng việc khớp mẫu rất tổng quát; chỉ cần các mẫu được cấu thành từ những cách nguyên thủy để xây dựng một kiểu (các trình tạo dữ liệu và các giá trị nguyên thủy), chúng là hợp lệ. Một dấu gạch dưới là một mẫu khớp mọi thứ.

Listing 4.18.
Parsing a command and argument string into a `Command` (DataStore.idr)

Bây giờ bạn có thể phân tích một chuỗi thành một Lệnh, bạn có thể tiến xa hơn với processInput, gọi parse. Nếu nó thất bại, bạn hiển thị một thông báo lỗi và giữ nguyên cửa hàng như hiện tại. Nếu không, bạn thêm một lỗ cho việc xử lý Lệnh:

processInput : DataStore -> String -> Maybe (String, DataStore) processInput store inp = case parse inp of Nothing => Just ("Invalid command\n", store) Just cmd => ?processCommand

4.3.4.
Processing commands

Một cách để tiến hành triển khai processInput của bạn là phân tách theo cmd và xử lý các lệnh trực tiếp:

processInput : DataStore -> String -> Maybe (String, DataStore) processInput store inp = case parse inp of Nothing => Just ("Invalid command\n", store) Just (Add item) => ?processCommand_1 Just (Get pos) => ?processCommand_2 Just Quit => ?processCommand_3

Bạn có thể hoàn thiện việc triển khai bằng cách lấp đầy các lỗ hổng dễ hơn, trong các trường hợp Thêm mục và Thoát. Danh sách tiếp theo cho thấy cách các lỗ hổng này được hoàn thiện, để lại processCommand_2 tạm thời.

Listing 4.19.
Processing the inputs `Add item` and `Quit` (DataStore.idr)

Luôn là một ý tưởng hay để kiểm tra các loại lỗ hổng mà Idris đã tạo ra để xem bạn có những biến nào, loại của chúng là gì và bạn cần loại nào để xây dựng. Đối với ?processCommand_2, bạn có điều này:

 pos : Integer store : DataStore input : String -------------------------------------- processCommand_2 : Maybe (String, DataStore)

Điều này sẽ phức tạp hơn một chút so với các trường hợp khác. Bạn cần thực hiện các bước sau:

Get the items from the store.
Ensure that the position, pos, is in range.
If it is, extract the item from the specified pos and return it along with the store itself.

Quá trình xác định-định nghĩa-tinh chỉnh khuyến khích bạn viết các phần của định nghĩa, từng bước một, liên tục kiểm tra loại khi bạn tiến hành, và liên tục xem xét các loại của các chỗ trống.

Bởi vì có một vài chi tiết liên quan đến việc điền vào lỗ ?processCommand_2, chúng tôi sẽ đổi tên nó thành ?getEntry và nâng nó lên thành một hàm cấp cao trước khi triển khai nó từng bước.

Type— Lift getEntry to a new top-level function:

getEntry : (pos : Integer) -> (store : DataStore) -> (input : String) -> Maybe (String, DataStore)

Define— Create a new skeleton definition:
```
getEntry pos store input = ?getEntry_rhs
```

Define— You’ll need the items in the store, so define a new local variable for these:

getEntry pos store input = let store_items = items store in ?getEntry_rhs

Inspecting the type of getEntry_rhs tells you the type of store_items:

 pos : Integer store : DataStore input : String store_items : Vect (size store) String -------------------------------------- getEntry_rhs : Maybe (String, DataStore)

Refine— To retrieve an entry from a Vect, you can use index as you’ve previously seen:
```
index : Fin n -> Vect n a -> a
```
To extract an entry from store_items, which has type Vect (size store), you’ll need a Fin (size store). Unfortunately, all you have available at the moment is an Integer. Using integerToFin, as described in section 4.2.3, you can refine the definition. If integerToFin returns Nothing, the input was out of bounds.
```
getEntry : (pos : Integer) -> (store : DataStore) -> (input : String) -> Maybe (String, DataStore) getEntry pos store input = let store_items = items store in case integerToFin pos (size store) of Nothing => Just ("Out of range\n", store) Just id => ?getEntry_rhs_2
```

Refine— If you inspect the type of getEntry_rhs_2 now, you’ll see that you have the Fin (size store) you need:

 store : DataStore id : Fin (size store) pos : Integer input : String store_items : Vect (size store) String -------------------------------------- getEntry_rhs_2 : Maybe (String, DataStore)

You can now refine to a complete definition:

getEntry : (pos : Integer) -> (store : DataStore) -> (input : String) Maybe (String, DataStore) getEntry pos store input = let store_items = items store in case integerToFin pos (size store) of Nothing => Just ("Out of range\n", store) Just id => Just (index id store_items ++ "\n", store)

Refine— As a final refinement, observe that input is never used, so you can remove this argument. Don’t forget to remove it from the application of get-Entry in processInput too.

getEntry : (pos : Integer) -> (store : DataStore) -> Maybe (String, DataStore) getEntry pos store = let store_items = items store in case integerToFin pos (size store) of Nothing => Just ("Out of range\n", store) Just id => Just (index id store_items ++ "\n", store)

Bằng cách sử dụng một Vect cho cửa hàng, với kích thước là một phần của kiểu, hệ thống kiểu có thể đảm bảo rằng bất kỳ truy cập nào vào cửa hàng thông qua chỉ số sẽ nằm trong giới hạn, vì bạn phải chứng minh rằng chỉ số có cùng giới hạn trên như độ dài của Vect.

Để tham khảo, việc triển khai hoàn chỉnh của kho dữ liệu được cung cấp trong danh sách dưới đây, với tất cả các chức năng mà chúng ta vừa làm việc qua.

Listing 4.20.
Complete implementation of a simple data store (DataStore.idr)

module Main import Data.Vect data DataStore : Type where MkData : (size : Nat) -> (items : Vect size String) -> DataStore size : DataStore -> Nat size (MkData size' items') = size' items : (store : DataStore) -> Vect (size store) String items (MkData size' items') = items' addToStore : DataStore -> String -> DataStore addToStore (MkData size store) newitem = MkData _ (addToData store) where addToData : Vect oldsize String -> Vect (S oldsize) String addToData [] = [newitem] addToData (x :: xs) = x :: addToData xs data Command = Add String | Get Integer | Quit parseCommand : String -> String -> Maybe Command parseCommand "add" str = Just (Add str) parseCommand "get" val = case all isDigit (unpack val) of False => Nothing True => Just (Get (cast val)) parseCommand "quit" "" = Just Quit parseCommand _ _ = Nothing parse : (input : String) -> Maybe Command parse input = case span (/= ' ') input of (cmd, args) => parseCommand cmd (ltrim args) getEntry : (pos : Integer) -> (store : DataStore) -> Maybe (String, DataStore) getEntry pos store = let store_items = items store in case integerToFin pos (size store) of Nothing => Just ("Out of range\n", store) Just id => Just (index id (items store) ++ "\n", store) processInput : DataStore -> String -> Maybe (String, DataStore) processInput store input = case parse input of Nothing => Just ("Invalid command\n", store) Just (Add item) => Just ("ID " ++ show (size store) ++ "\n", addToStore store item) Just (Get pos) => getEntry pos store Just Quit => Nothing main : IO () main = replWith (MkData _ []) "Command: " processInput

Exercises

Add a size command that displays the number of entries in the store.
Add a search command that displays all the entries in the store containing a given substring. Hint: Use Strings.isInfixOf.

Extend search to print the location of each result, as well as the string. You can test your solution at the REPL as follows:

*ex_4_3> :exec Command: add Shearer ID 0 Command: add Milburn ID 1 Command: add White ID 2 Command: size 3 Command: search Mil 1: Milburn

4.4. Summary

Data types are defined in terms of a type constructor and data constructors.
Enumeration types are defined by listing the data constructors of the type.
Union types are defined by listing the data constructors of the type, each of which may carry additional information.
Generic types are parameterized over some other type. In a generic type definition, variables stand in place of concrete types.
Dependent types can be indexed over any other value.
Using dependent types, you can classify a larger family of types (such as vehicles) into smaller subgroups (such as vehicles powered by petrol and those powered by pedal) in the same declaration.
Dependent types allow safety checks to be guaranteed at compile time, such as guaranteeing that all vector accesses are within the bounds of the vector.
You can write larger programs in the type-driven style, creating new data types where appropriate to help describe components of the system.
Interactive programs that involve state can be written using the replWith function.

Chapter 5.
Interactive programs: input and output processing

Chương này đề cập đến

Writing interactive console programs
Distinguishing evaluation and execution
Validating user inputs to dependently typed functions

Idris là một ngôn ngữ thuần túy, có nghĩa là các hàm không có tác dụng phụ, chẳng hạn như cập nhật các biến toàn cục, ném ngoại lệ, hoặc thực hiện việc nhập hoặc xuất ra console. Tuy nhiên, khi chúng ta kết hợp các hàm lại với nhau để tạo ra các chương trình hoàn chỉnh, chúng ta sẽ cần tương tác với người dùng bằng cách nào đó.

Trong các chương trước, chúng ta đã sử dụng các hàm repl và replWith để viết các chương trình tương tác đơn giản, lặp đi lặp lại mà chúng ta có thể biên dịch và thực thi mà không cần quá lo lắng về cách chúng hoạt động. Tuy nhiên, đối với tất cả các chương trình không đơn giản, cách tiếp cận này là rất hạn chế. Trong chương này, bạn sẽ thấy cách mà các chương trình tương tác hoạt động trong Idris một cách tổng quát hơn. Bạn sẽ thấy cách xử lý và xác thực đầu vào của người dùng, và cách bạn có thể viết các chương trình tương tác hoạt động với các loại phụ thuộc.

Ý tưởng chính cho phép chúng ta viết các chương trình tương tác trong Idris, mặc dù đây là một ngôn ngữ thuần túy, là chúng ta phân biệt giữa đánh giá và thực thi. Chúng ta viết các chương trình tương tác bằng cách sử dụng một kiểu tổng quát IO, mô tả các chuỗi hành động sau đó được thực thi bởi hệ thống thời gian chạy của Idris.

5.1. Interactive programming with IO

Mặc dù bạn không thể viết các hàm tương tác trực tiếp với người dùng, nhưng bạn có thể viết các hàm mô tả các chuỗi tương tác. Khi bạn có một mô tả về chuỗi tương tác, bạn có thể truyền nó cho môi trường runtime của Idris, nơi sẽ thực thi các hành động đó.

Prelude cung cấp một kiểu tổng quát, IO, cho phép bạn mô tả các chương trình tương tác trả về một giá trị:

Idris> :doc IO IO : (res : Type) -> Type Interactive programs, describing I/O actions and returning a value. Arguments: res : Type -- The result type of the program

Do đó, bạn phân biệt trong loại giữa các hàm mô tả tương tác với người dùng và các hàm trả về giá trị trực tiếp.

Ví dụ, hãy xem xét sự khác biệt giữa các loại hàm String -> Int và String -> IO Int:

String -> Int is the type of a function that takes a String as an input and returns an Int without any user interaction or side effects.
String -> IO Int is the type of a function that takes a String as an input and returns a description of an interactive program that produces an Int.

Dưới đây là một vài ví dụ về các hàm với các loại này:

length : String -> Int, which is defined in the Prelude, returns the length of the input String.
readAndGetLength : String -> IO Int returns a description of interactive actions that display the input String as a prompt, reads another String from the console, and then returns the length of that String.

Như bạn đã thấy trong các chương trước, điểm vào của một ứng dụng Idris là main : IO (), và chúng ta đã sử dụng điều này để viết các vòng lặp tương tác đơn giản bằng cách sử dụng các chức năng repl và replWith mà không quá lo lắng về chi tiết cách mà những chức năng này hoạt động. Giờ là lúc để xem xét IO một cách chi tiết hơn, và học cách viết các chương trình tương tác phức tạp hơn.

Danh sách 5.1 cho thấy một ví dụ về một chương trình tương tác trả về mô tả các hành động để hiển thị một lời nhắc, đọc tên người dùng và sau đó hiển thị một lời chào. Chúng ta sẽ xem xét các chi tiết của cú pháp trong suốt phần này, nhưng bây giờ, hãy chú ý đến kiểu của main : IO (). Kiểu này cho biết rằng main không nhận đầu vào và trả về một mô tả về các hành động tương tác tạo ra một bộ rỗng.

Listing 5.1.
A simple interactive program, reading a user’s name and displaying a greeting (Hello.idr)

IO in Haskell and Idris

Nếu bạn đã quen thuộc với Haskell, bạn sẽ thấy rằng lập trình với IO trong Idris rất giống với việc viết các chương trình tương tác trong Haskell. Nếu bạn hiểu danh sách 5.1, bạn có thể an tâm chuyển sang phần 5.3, nơi bạn sẽ thấy cách xác thực đầu vào của người dùng và xử lý lỗi trong các chương trình Idris tương tác. Bạn cũng có thể muốn xem phần 5.2.2, bàn về giới hạn kiểu theo mẫu.

Trong phần này, bạn sẽ học cách viết các chương trình tương tác như thế này sử dụng IO trong Idris và khám phá sự khác biệt giữa việc đánh giá các biểu thức và thực thi các chương trình, điều này cho phép chúng ta viết các chương trình tương tác mà không làm tổn hại đến tính thuần khiết.

5.1.1.
Evaluating and executing interactive programs

Các hàm trả về kiểu IO vẫn được coi là thuần khiết, vì chúng chỉ mô tả các hành động tương tác. Ví dụ, hàm putStrLn được định nghĩa trong Prelude và trả về các hành động xuất một chuỗi String đã cho, cộng với một ký tự xuống dòng, ra màn hình console:

Idris> :t putStrLn putStrLn : String -> IO ()

Khi bạn nhập một biểu thức tại REPL, Idris sẽ đánh giá biểu thức đó. Nếu biểu thức đó là mô tả các hành động tương tác, thì để thực hiện những hành động đó cần một bước bổ sung, đó là thực thi.

Hình 5.1 minh họa điều gì xảy ra khi biểu thức putStrLn (show (47 * 2)) được thực thi. Trước tiên, Idris tính toán rằng hành động tương tác là hiển thị "94\n" trên bảng điều khiển (tức là, bộ đánh giá tính toán chuỗi chính xác sẽ được hiển thị), và sau đó nó chuyển hành động đó đến môi trường thời gian thực.

Figure 5.1.
Evaluating the expression `putStrLn (show (47 * 2))` and then executing the resulting actions

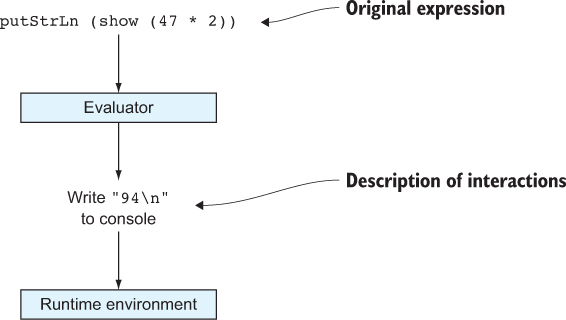
Bạn có thể thấy điều gì xảy ra bằng cách đánh giá biểu thức putStrLn (show (47 * 2)) tại REPL. Điều này chỉ đơn thuần cho thấy một mô tả về các hành động mà một môi trường runtime có thể thực hiện. Không cần phải xem xét kỹ hình thức chính xác của kết quả ở đây, nhưng bạn có thể ít nhất thấy rằng việc đánh giá tạo ra một biểu thức có kiểu IO ().

Idris> putStrLn (show (47 * 2)) io_bind (prim_write "94\n") (\__bindx => io_return ()) : IO ()

Nếu bạn muốn thực hiện các hành động kết quả, bạn sẽ cần truyền mô tả này đến môi trường thực thi Idris. Bạn có thể đạt được điều này bằng cách sử dụng lệnh :exec trong REPL:

Idris> :exec putStrLn (show (47 * 2)) 94

Nói chung, lệnh :exec, khi nhận một biểu thức loại IO (), có thể được hiểu là thực hiện các thao tác sau:

Evaluate the expression, producing a description of the interactive actions to execute. In figure 5.1, evaluating the expression produces a description of an action: Write the string "94\n" to the console.
Pass the resulting actions to the runtime environment, which executes them. In figure 5.1, executing the actions writes the string "94\n" to the console.

Cũng có thể biên dịch thành một tệp thực thi độc lập bằng cách sử dụng lệnh :c tại REPL, lệnh này nhận tên tệp thực thi làm tham số và tạo ra một chương trình thực hiện các hành động được mô tả trong hàm main. Ví dụ, hãy quay lại danh sách 5.1, được lặp lại ở đây:

module Main main : IO () main = do putStr "Enter your name: " x <- getLine putStrLn ("Hello " ++ x ++ "!")

Nếu bạn lưu điều này trong một tệp, Hello.idr, và tải nó trong REPL, bạn có thể tạo ra một tệp thực thi như sau:

*Hello> :c hello

Điều này dẫn đến một tệp thực thi có tên là hello (hoặc, trên các hệ thống Windows, hello.exe) mà có thể được chạy trực tiếp từ shell. Ví dụ:

$ ./hello Enter your name: Edwin Hello Edwin!

Ở đây, hàm main không chỉ mô tả một hành động mà là một chuỗi các hành động. Nói chung, trong các chương trình tương tác, bạn cần có khả năng sắp xếp các hành động và các lệnh phải phản ứng với đầu vào của người dùng. Do đó, Idris cung cấp các phương tiện để kết hợp các chương trình tương tác nhỏ hơn thành những chương trình lớn hơn. Chúng ta sẽ bắt đầu bằng cách xem xét cách thực hiện điều này bằng một hàm Prelude, (>>=), và sau đó chúng ta sẽ xem xét cú pháp cao cấp mà chúng ta đã sử dụng trước đó trong danh sách 5.1, ký hiệu do.

5.1.2.
Actions and sequencing: the >>= operator

Trong ví dụ ngắn ở danh sách 5.1, chúng tôi đã sử dụng ba hành động IO:

putStr : String -> IO (), which is an action to display a String on the console
putStrLn : String -> IO (), which is an action to display a String followed by a newline on the console
getLine : IO String, which is an action to read a String from the console

Để viết các chương trình thực tế, bạn sẽ cần làm nhiều hơn là chỉ thực hiện các hành động. Bạn cần có khả năng sắp xếp các hành động và bạn cũng cần có khả năng xử lý kết quả của các hành động đó.

Giả sử, ví dụ như, bạn muốn đọc một chuỗi từ console và sau đó xuất ra độ dài của nó. Có một hàm length trong Prelude, có kiểu String -> Int, mà bạn có thể sử dụng để tính toán độ dài của một chuỗi, nhưng getLine trả về một giá trị có kiểu IO String, chứ không phải String. Kiểu IO String là một mô tả về một hành động tạo ra một String, không phải là chính String đó.

Nói cách khác, bạn có thể truy cập vào chuỗi được đọc từ màn hình khi các hành động bắt nguồn từ hàm được thực thi, nhưng bạn chưa có quyền truy cập vào nó khi hàm được đánh giá. Không có hàm nào có kiểu IO String -> String. Nếu hàm như vậy tồn tại, điều đó có nghĩa là có thể biết được chuỗi nào đã được đọc từ màn hình mà không thực sự đọc bất kỳ chuỗi nào từ màn hình!

Prelude cung cấp một hàm gọi là >>= (dự định được sử dụng như một toán tử giữa) cho phép sắp xếp các hành động IO, cung cấp kết quả của một hành động làm đầu vào cho hành động tiếp theo. Nó có kiểu sau:

(>>=) : IO a -> (a -> IO b) -> IO b

Hình 5.2 cho thấy một ứng dụng ví dụ của >>= để nối hai hành động, sử dụng đầu ra của hành động đầu tiên, getLine, làm đầu vào cho hành động thứ hai, putStrLn. Bởi vì getLine trả về một giá trị có kiểu IO String, Idris mong đợi rằng putStrLn nhận một String làm đối số của nó.

Figure 5.2.
An interactive operation to read a `String` and then echo its contents using the `>>=` operator. The types of each subexpression are indicated.

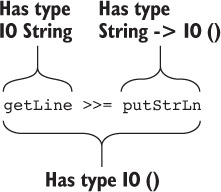
Bạn có thể thực hiện bất kỳ chuỗi hành động nào có kiểu IO () tại REPL bằng cách sử dụng lệnh :exec, vì vậy bạn có thể thực hiện các thao tác trong hình 5.2 như sau:

Để minh họa thêm, hãy thử sử dụng >>= để viết một hàm printLength đọc một chuỗi từ bảng điều khiển và sau đó xuất độ dài của nó. Để làm điều này, hãy thực hiện các bước sau:

Type— Our printLength function takes no input and returns a description of IO actions, so give it the following type:
```
printLength : IO ()
```
Define— The function has a skeleton definition that takes no arguments:
```
printLength : IO () printLength = ?printLength_rhs
```
Refine— Refine the printLength_rhs hole to call getLine for a description of an action that reads from the console, and use >>= to pass the value produced by getLine when it’s executed to the next action. Leave a hole in place of the next action for the moment:
```
printLength : IO () printLength = getLine >>= ?printLength_rhs
```
Type— If you inspect the type of ?printLength_rhs, you’ll see that it has a function type:
```
-------------------------------------- printLength_rhs : String -> IO ()
```
The String in the function type here is the value that will be produced by executing getLine. This string will be available when the action is executed, and you can use it to compute the remaining IO actions.
Refine— An expression search on ?printLength_rhs will give you an anonymous function:
```
printLength : IO () printLength = getLine >>= \result => ?printLength_rhs1
```
The variable result is the String produced by the getLine action. Rename this to something more informative, like input:
```
printLength : IO () printLength = getLine >>= \input => ?printLength_rhs1
```
Refine— Because input is a String, you can use length to calculate its length as a Nat. Use a let binding to store this in a local variable:
```
printLength : IO () printLength = getLine >>= \input => let len = length input in ?printLength_rhs1
```
Refine—
Finally, complete the definition using show to convert len to a String, and putStrLn to give an action that displays the result:
```
printLength : IO () printLength = getLine >>= \input => let len = length input in putStrLn (show len)
```

Bạn có thể thử định nghĩa này tại REPL với :exec printLength, cho Idris biết rằng bạn muốn thực thi các hành động kết quả thay vì chỉ đơn giản đánh giá biểu thức.

Danh sách 5.2 hiển thị định nghĩa hoàn chỉnh, được làm tinh tế hơn bằng cách hiển thị một thông báo. Bố cục cũng đã được điều chỉnh trong định nghĩa này để làm nổi bật trình tự các hành động.

Listing 5.2.
A function to display a prompt, read a string, and then display its length, using `>>=` to sequence `IO` actions (PrintLength.idr)

The type of >>=

Nếu bạn kiểm tra kiểu của >>= tại REPL, bạn sẽ thấy một kiểu tổng quát bị ràng buộc:

Idris> :t (>>=) (>>=) : Monad m => m a -> (a -> m b) -> m b

Trên thực tế, điều này có nghĩa là mẫu này áp dụng rộng rãi hơn so với IO, và bạn sẽ thấy nhiều hơn về điều này sau. Hiện tại, chỉ cần đọc biến kiểu m ở đây là IO.

Về nguyên tắc, bạn luôn có thể sử dụng >>= để tuần tự hóa các hành động IO, truyền đầu ra của một hành động làm đầu vào cho hành động tiếp theo. Tuy nhiên, các định nghĩa thu được có phần xấu xí, và việc tuần tự hóa các hành động là rất phổ biến. Đó là lý do tại sao Idris cung cấp một cú pháp thay thế cho việc tuần tự hóa các hành động IO, đó là cú pháp do.

5.1.3.
Syntactic sugar for sequencing with do notation

Các chương trình tương tác thường mang tính mệnh lệnh theo cách tự nhiên, với một chuỗi các lệnh, mỗi lệnh đều tạo ra một giá trị có thể được sử dụng sau này. Hàm >>= nắm bắt ý tưởng này, nhưng các định nghĩa kết quả có thể khó đọc.

Thay vào đó, bạn có thể sắp xếp các hành động IO bên trong các khối do, cho phép bạn liệt kê các hành động sẽ được thực hiện khi một khối được thực thi. Ví dụ, để in hai thứ liên tiếp, bạn sẽ làm điều gì đó như sau:

printTwoThings : IO () printTwoThings = do putStrLn "Hello" putStrLn "World"

Idris chuyển đổi cú pháp do thành các phép gọi của >>=. Hình 5.3 cho thấy cách mà điều này hoạt động trong trường hợp đơn giản nhất, nơi một hành động được thực thi, tiếp theo là các hành động khác.

Figure 5.3.
Transforming `do` notation to an expression using the `>>=` operator when sequencing actions. The value produced by the action, of type `ty`, is ignored, as indicated by the underscore.

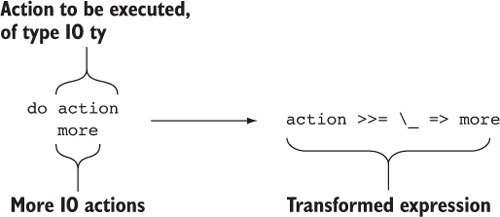
Kết quả của một hành động có thể được gán cho một biến. Ví dụ, để gán kết quả của việc đọc từ bảng điều khiển với getLine cho biến x và sau đó in kết quả, bạn có thể viết như sau:

printInput : IO () printInput = do x <- getLine putStrLn x

Ký hiệu x <- getLine cho biết rằng kết quả của hành động getLine (tức là, chuỗi được tạo ra bởi hành động có kiểu IO String) sẽ được lưu trữ trong biến x, mà bạn có thể sử dụng trong phần còn lại của khối do. Việc sắp xếp các hành động và ràng buộc một biến như thế này bằng cách sử dụng ký hiệu do sẽ được dịch trực tiếp thành các phép gọi của >>=, như được minh họa trong hình 5.4.

Figure 5.4.
Transforming `do` notation to an expression using the `>>=` operator, when binding a variable and sequencing actions

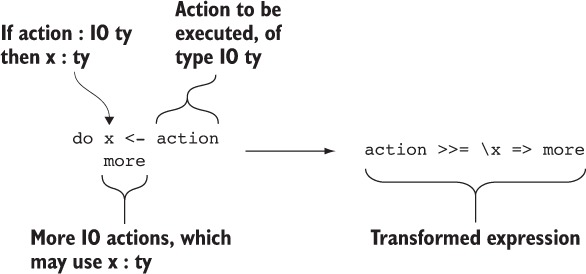
Bạn cũng có thể sử dụng let bên trong các khối do để gán một biểu thức thuần cho một biến. Danh sách sau cho thấy cách mà printLength có thể được viết bằng cách sử dụng ký hiệu do thay vì sử dụng >>= trực tiếp.

Listing 5.3.
A function to display a prompt, read a string, and then display its length using `do` notation to sequence `IO` actions (PrintLength.idr)

let and <- in do blocks

Hàm printLength trong danh sách 5.3 sử dụng hai dạng khác nhau để gán cho các biến: sử dụng let và sử dụng <-. Có một sự khác biệt quan trọng giữa hai cách này, dựa trên sự phân biệt giữa đánh giá và thực thi:

Use let x = expression to assign the result of the evaluation of an expression to a variable.
Use x <- action to assign the result of the execution of an action to a variable.

Trong danh sách 5.3, getLine mô tả một hành động, vì vậy nó cần phải được thực thi và kết quả được gán bằng <-, nhưng độ dài input thì không, nên nó được gán bằng let.

Hầu hết các định nghĩa tương tác trong Idris được viết bằng cách sử dụng cú pháp do để kiểm soát thứ tự thực hiện. Trong các chương trình lớn hơn, bạn cũng sẽ cần phải phản hồi lại đầu vào của người dùng và điều hướng luồng chương trình. Ở phần tiếp theo, chúng ta sẽ xem xét các phương pháp khác nhau để đọc và phản hồi đối với đầu vào của người dùng, cũng như cách thực hiện vòng lặp và các hình thức kiểm soát luồng khác trong các chương trình tương tác.

Exercises

Using do notation, write a printLonger program that reads two strings and then displays the length of the longer string.
Write the same program using >>= instead of do notation. You can test your answers at the REPL as follows:
```
*ex_5_1> :exec printLonger First string: short Second string: longer 6
```

5.2. Interactive programs and control flow

Bạn đã thấy cách viết các chương trình tương tác cơ bản bằng cách sắp xếp các hành động hiện có, chẳng hạn như getLine để đọc đầu vào từ bảng điều khiển và putStrLn để hiển thị văn bản trên bảng điều khiển. Nhưng khi các chương trình trở nên lớn hơn, bạn sẽ cần nhiều kiểm soát hơn: bạn sẽ cần có khả năng xác thực và phản hồi lại đầu vào của người dùng, và bạn sẽ cần diễn đạt vòng lặp cũng như các hình thức kiểm soát khác.

Nói chung, luồng điều khiển trong các hàm mô tả các hành động tương tác hoạt động chính xác giống như luồng điều khiển trong các hàm thuần túy, thông qua việc khớp mẫu và đệ quy. Cuối cùng, các hàm mô tả các hành động tương tác cũng là các hàm thuần túy, chỉ đơn thuần mô tả các hành động sẽ được thực hiện sau.

Trong phần này, chúng ta sẽ xem xét một số mẫu phổ biến mà thường gặp trong các chương trình tương tác: sản xuất các giá trị thuần khiết bằng cách kết hợp các kết quả của các hành động tương tác, khớp mẫu trên các kết quả của các hành động tương tác, và cuối cùng, kết hợp mọi thứ lại trong một chương trình tương tác với các vòng lặp.

5.2.1.
Producing pure values in interactive definitions

Ngoài việc mô tả các hành động để thực hiện bởi hệ thống thực thi, bạn thường muốn tạo ra kết quả từ các chương trình tương tác. Bạn đã thấy getLine, ví dụ:

getLine : IO String

Kiểu IO String nói rằng đây là một hàm mô tả các hành động tạo ra một String như là kết quả.

Thường thì bạn sẽ muốn viết một hàm sử dụng một hành động IO như getLine và sau đó thao tác với kết quả của nó trước khi trả về. Ví dụ, bạn có thể muốn viết một hàm readNumber mà đọc một chuỗi từ console và chuyển đổi nó thành Nat nếu đầu vào hoàn toàn là chữ số. Nó trả về một giá trị thuộc kiểu Maybe Nat:

If the input consists entirely of digits representing the number i, it produces Just i. For example, on reading the string "1234", it produces Just 1234.
Otherwise, it produces Nothing.

Danh sách 5.4 cho thấy cách định nghĩa readNumber. Sau khi đọc một đầu vào bằng cách sử dụng getLine, nó kiểm tra xem mọi ký tự trong đầu vào có phải là chữ số hay không. Nếu đúng, nó chuyển đổi đầu vào thành một Nat, tạo ra kết quả bằng cách sử dụng Just; nếu không, nó sẽ sản xuất Nothing.

Listing 5.4.
Reading and validating a number (ReadNum.idr)

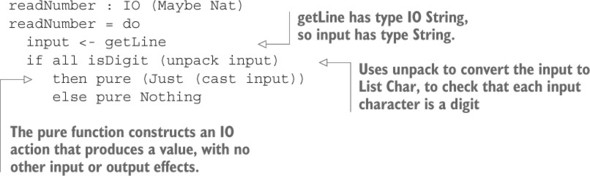
Hàm thuần khiết được sử dụng để tạo ra một giá trị trong một chương trình tương tác mà không có bất kỳ ảnh hưởng đầu vào hoặc đầu ra nào khi nó được thực thi. Mục đích của nó là cho phép các giá trị thuần khiết được xây dựng bởi các chương trình tương tác, như được thể hiện bởi kiểu của nó:

pure : a -> IO a

Để hiểu nhu cầu về pure trong readNumber, bạn có thể thay thế các nhánh then và else của câu lệnh if bằng các khoảng trống, và kiểm tra các kiểu của chúng:

readNumber : IO (Maybe Nat) readNumber = do input <- getLine if all isDigit (unpack input) then ?numberOK else ?numberBad

"Nếu bạn nhìn vào kiểu của ?numberOK, bạn sẽ thấy rằng bạn cần một giá trị của kiểu IO (Có thể Nat):"

 input : String -------------------------------------- numberOK : IO (Maybe Nat)

Bạn có thể tinh chỉnh các lỗ ?numberOK và ?numberBad bằng cách sử dụng pure:

readNumber : IO (Maybe Nat) readNumber = do input <- getLine if all isDigit (unpack input) then pure ?numberOK else pure ?numberBad

Bây giờ, nếu bạn nhìn vào loại của ?numberOK, bạn sẽ thấy rằng bạn cần một giá trị có kiểu Maybe Nat thay vào đó, không có lớp bọc IO.

 input : String -------------------------------------- numberOK : Maybe Nat

Type of pure

Giống như với >>=, nếu bạn kiểm tra kiểu của pure tại REPL, bạn sẽ thấy một kiểu tổng quát bị ràng buộc, chứ không phải là một kiểu sử dụng cụ thể IO:

Idris> :t pure pure : Applicative f => a -> f a

Bạn có thể đọc f ở đây như IO. Chúng ta sẽ đi đến nghĩa chính xác của Applicative và Monad ở chương 7; bạn không cần phải hiểu các chi tiết để viết chương trình tương tác.

Bạn có thể thử đọc số tại REPL bằng cách thực thi nó và chuyển kết quả cho printLn (được mô tả trong thanh bên, “Hiển thị giá trị với printLn”):

Trong trường hợp đầu tiên, đầu vào hợp lệ, vì vậy Idris trả về kết quả Just 100. Trong trường hợp thứ hai, đầu vào có ký tự không phải là chữ số, vì vậy Idris trả về Nothing.

Displaying values with printLn

`printLn là sự kết hợp của putStrLn và show, và nó rất tiện lợi để hiển thị giá trị trực tiếp trên console. Nó được định nghĩa trong Prelude:`

printLn : Show a => a -> IO () printLn x = putStrLn (show x)

5.2.2.
Pattern-matching bindings

Khi một hành động tương tác tạo ra một giá trị của một kiểu dữ liệu phức tạp nào đó, chẳng hạn như readNumber, cái mà tạo ra một giá trị kiểu Maybe Nat, bạn thường muốn thực hiện việc phân tích mẫu trên kết quả trung gian. Bạn có thể làm điều này bằng cách sử dụng biểu thức case, nhưng điều này có thể dẫn đến các định nghĩa lồng nhau sâu. Ví dụ, danh sách sau đây cho thấy một hàm đọc hai số từ bảng điều khiển bằng cách sử dụng readNumber, và tạo ra một cặp các số đó nếu cả hai là đầu vào hợp lệ, hoặc Nothing nếu không.

Listing 5.5.
Reading and validating a pair of numbers from the console (ReadNum.idr)

Điều này chỉ càng trở nên tồi tệ hơn khi các hàm trở nên dài hơn và có nhiều điều kiện lỗi hơn cần xử lý. Để giúp giải quyết vấn đề này, Idris cung cấp cú pháp ngắn gọn để khớp với các giá trị trung gian trong cú pháp do. Đầu tiên, chúng ta sẽ xem xét một ví dụ đơn giản, đọc một cặp chuỗi từ bảng điều khiển, sau đó chúng ta sẽ quay lại hàm readNumbers và xem cách nó có thể được làm ngắn gọn hơn.

Bạn có thể viết một hàm đọc hai chuỗi và tạo ra một cặp như sau, sử dụng pure để kết hợp hai đầu vào:

readPair : IO (String, String) readPair = do str1 <- getLine str2 <- getLine pure (str1, str2)

Khi bạn sử dụng kết quả được tạo ra bởi readPair, bạn sẽ cần phải thực hiện thao tác khớp mẫu để trích xuất đầu vào đầu tiên và thứ hai. Ví dụ, để đọc một cặp chuỗi sử dụng readPair và sau đó hiển thị cả hai, bạn sẽ làm như sau:

usePair : IO () usePair = do pair <- readPair case pair of (str1, str2) => putStrLn ("You entered " ++ str1 ++ " and " ++ str2)

Để làm cho các chương trình này ngắn gọn hơn, Idris cho phép kết hợp việc khớp mẫu và gán giá trị trên một dòng trong một phép gán khớp mẫu. Chương trình sau đây có hành vi hoàn toàn giống với chương trình trước:

usePair : IO () usePair = do (str1, str2) <- readPair putStrLn ("You entered " ++ str1 ++ " and " ++ str2)

Một ý tưởng tương tự áp dụng cho readNumbers. Bạn có thể khớp mẫu trực tiếp trên kết quả của readNumber để kiểm tra tính hợp lệ của kết quả đó:

readNumbers : IO (Maybe (Nat, Nat)) readNumbers = do Just num1_ok <- readNumber Just num2_ok <- readNumber pure (Just (num1_ok, num2_ok))

Điều này hoạt động như bạn muốn khi người dùng nhập các số hợp lệ:

Tuy nhiên, thật không may, nó không xử lý trường hợp mà readNumber trả về Nothing, và do đó gặp sự cố khi thực thi:

Idris đã nhận thấy điều này khi kiểm tra readNumbers để đảm bảo tính toàn vẹn.

*ReadNum> :total readNumbers_v2 Main.readNumbers is possibly not total due to: Main.case block in readNumbers at ReadNum.idr:26:22, which is not total as there are missing cases

Remember to check totality!

Định nghĩa chưa hoàn chỉnh của hàm readNumbers minh họa tại sao việc kiểm tra rằng các hàm là toàn phần là quan trọng. Mặc dù readNumbers đã kiểm tra kiểu thành công, nhưng nó vẫn có thể thất bại ở thời gian chạy do thiếu các trường hợp.

Danh sách 5.6 cho thấy cách bạn có thể xử lý các khả năng khác trong một phép gán theo mẫu. Ngoài phép gán chính, bạn cung cấp các phép so sánh thay thế sau một dấu gạch đứng, cho thấy cách phần còn lại của hàm nên tiến hành nếu phép so sánh mặc định với Just num1_ok hoặc Just num2_ok không thành công. Hàm này có hành vi hoàn toàn giống với hàm trước đó trong danh sách 5.5.

Listing 5.6.
Reading and validating a pair of numbers from the console, concisely (ReadNum.idr)

Các ràng buộc khớp mẫu theo hình thức này cho phép bạn diễn đạt hành vi hợp lệ mong đợi của một hàm trong các trường hợp mặc định (Just num1_ok và Just num2_ok trong danh sách 5.6), xử lý các trường hợp lỗi trong các trường hợp thay thế.

5.2.3.
Writing interactive definitions with loops

Bây giờ bạn có thể đọc, xác thực và phản hồi đầu vào của người dùng, hãy kết hợp mọi thứ lại và viết các định nghĩa tương tác với vòng lặp.

Bạn có thể viết vòng lặp bằng cách viết các định nghĩa đệ quy. Danh sách tiếp theo, chẳng hạn, hiển thị một hàm đếm ngược tính toán một chuỗi các hành động để hiển thị một đếm ngược, với khoảng dừng một giây giữa mỗi số được hiển thị.

Listing 5.7.
Display a countdown, pausing one second between each iteration (Loops.idr)

Nếu bạn thử thực thi điều này tại REPL bằng :exec, bạn sẽ thấy một bộ đếm ngược được hiển thị:

*Loops> :exec countdown 5 5 4 3 2 1 Lift off!

Bạn cũng có thể kiểm tra xem hàm này có phải là tổng quát, tức là đảm bảo sản xuất kết quả trong thời gian hữu hạn cho tất cả các đầu vào khả thi hay không:

*Loops> :total countdown Main.countdown is Total

Nói chung, bạn có thể viết một hàm tương tác mô tả một vòng lặp bằng cách gọi đệ quy hàm với hành động cuối cùng của nó. Trong countdown, miễn là tham số đầu vào không phải là Z, chương trình khi được thực thi sẽ in ra tham số và chờ một giây trước khi thực hiện gọi đệ quy cho số nhỏ hơn tiếp theo. Số lần lặp của vòng lặp do đầu vào ban đầu xác định. Bởi vì điều này là hữu hạn, countdown chắc chắn phải kết thúc, vì vậy Idris cho biết rằng nó là tổng quát.

Totality and interactive programs

Kiểm tra tổng quát dựa trên đánh giá, không phải thực thi. Kết quả của việc kiểm tra tổng quát một chương trình IO, do đó, cho bạn biết liệu Idris sẽ tạo ra một chuỗi hành động hữu hạn hay không, nhưng không nói gì về hành vi thời gian chạy của những hành động đó.

Đôi khi, số lượng lần lặp lại được xác định bởi đầu vào của người dùng. Ví dụ, bạn có thể viết một hàm để tiếp tục thực hiện đếm ngược cho đến khi người dùng muốn dừng, như được thể hiện dưới đây.

Listing 5.8.
Keep running `countdown` until the user doesn’t want to run it any more (Loops.idr)

Chức năng này không đầy đủ, vì không có đảm bảo rằng người dùng sẽ bao giờ nhập bất kỳ thứ gì khác ngoài y, hoặc thậm chí cung cấp bất kỳ đầu vào hợp lệ nào.

*Loops> :total countdowns Main.countdowns is possibly not total due to recursive path: Main.countdowns

Các chương trình tương tác có thể chạy mãi mãi, chẳng hạn như đếm ngược (hoặc, một cách thực tế hơn, các máy chủ hoặc hệ điều hành), không phải là tổng quát, ít nhất là nếu chúng ta giới hạn định nghĩa cho các chương trình kết thúc. Chính xác hơn, một hàm tổng quát phải hoặc kết thúc hoặc được đảm bảo sẽ sản sinh một tiền tố hữu hạn của một đầu vào vô hạn, trong khoảng thời gian hữu hạn. Chúng ta sẽ thảo luận thêm về điều này trong chương 11.

Exercises

Write a function that implements a simple “guess the number” game. It should have the following type:
```
guess : (target : Nat) -> IO ()
```
Here, target is the number to be guessed, and guess should behave as follows:
- Repeatedly ask the user to guess a number, and display whether the guess is too high, too low, or correct.
- When the guess is correct, exit.
Ideally, guess will also report an error message if the input is invalid (for example, if it contains characters that are not digits or are out of range).
Implement a main function that chooses a random number between 1 and 100 and then calls guess. Hint: As a source of random numbers, you could use time : IO Integer, defined in the System module.
Extend guess so that it counts the number of guesses the user has taken and displays that number before the input is read. Hint: Refine the type of guess to the following:
```
guess : (target : Nat) -> (guesses : Nat) -> IO ()
```
Implement your own versions of repl and replWith. Remember that you’ll need to use different names to avoid clashing with the names defined in the Prelude.

5.3. Reading and validating dependent types

Trong các chương trước, bạn đã thấy một số hàm với các kiểu phụ thuộc, đặc biệt là sử dụng Vect để biểu diễn độ dài của các vectơ trong kiểu của chúng. Điều này cho phép bạn tuyên bố các giả định về hình thức của đầu vào cho một hàm trong kiểu của nó và đảm bảo về hình thức đầu ra của nó. Ví dụ, bạn đã thấy hàm zip, hàm này kết hợp các phần tử tương ứng của các vectơ.

zip : Vect n a -> Vect n b -> Vect n (a, b)

Loại này biểu thị những điều sau:

Assumption— Both input vectors have the same length, n.
Guarantee— The output vector will have the same length as the input vectors.
Guarantee—
The output vector will consist of pairs of the element type of the first input vector and the element type of the second input vector.

Idris kiểm tra rằng bất cứ khi nào hàm được gọi, các tham số thỏa mãn giả định và định nghĩa của hàm thỏa mãn đảm bảo.

Cho đến nay, chúng tôi đã thử nghiệm các hàm như zip tại REPL. Tuy nhiên, một cách thực tế, đầu vào cho các hàm không đến từ một môi trường được kiểm soát cẩn thận như nơi có trình kiểm tra kiểu Idris. Trong thực tế, khi một chương trình hoàn chỉnh được biên dịch và thực thi, đầu vào cho các hàm sẽ đến từ một nguồn bên ngoài: có thể là một trường trên trang web, hoặc đầu vào của người dùng tại bảng điều khiển.

Khi một chương trình đọc dữ liệu từ một nguồn bên ngoài, nó không thể đưa ra bất kỳ giả định nào về hình thức của dữ liệu đó. Thay vào đó, chương trình phải kiểm tra rằng dữ liệu ở dạng cần thiết. Kiểu của một hàm cho bạn biết chính xác những gì bạn cần kiểm tra để đánh giá nó một cách an toàn.

Trong phần này, chúng ta sẽ viết một chương trình đọc hai vectơ từ bảng điều khiển, sử dụng hàm zip để ghép các phần tử tương ứng nếu các vectơ có cùng độ dài, và sau đó hiển thị kết quả. Mặc dù đây là một mục tiêu đơn giản, nó thể hiện một số khía cạnh quan trọng trong việc làm việc với các kiểu phụ thuộc trong các chương trình tương tác, và bạn sẽ thấy nhiều ví dụ hơn về hình thức này sau trong cuốn sách này. Bạn sẽ thấy, một cách ngắn gọn, cách mà các kiểu của các phần thuần túy của chương trình cho bạn biết những gì bạn cần kiểm tra trong các phần tương tác, và cách mà hệ thống kiểu dẫn dắt bạn đến các phần mà kiểm tra lỗi là cần thiết.

5.3.1.
Reading a Vect from the console

Là bước đầu tiên, bạn cần có khả năng đọc một vector từ console. Bởi vì vector thể hiện chiều dài của chúng trong kiểu dữ liệu, bạn sẽ cần một cách nào đó để mô tả chiều dài của vector mà bạn dự định đọc. Một cách là lấy chiều dài như một đầu vào, chẳng hạn như trong kiểu sau:

readVectLen : (len : Nat) -> IO (Vect len String)

Loại này cho biết readVectLen nhận một chiều dài dự kiến làm đầu vào và trả về chuỗi các hành động đọc một vector của các chuỗi có độ dài đó. Danh sách dưới đây cho thấy một cách bạn có thể triển khai hàm này.

Listing 5.9.
Reading a `Vect` of known length from the console (ReadVect.idr)

Bạn có thể thử readVectLen tại REPL bằng cách thực thi nó với một độ dài cụ thể, và sau đó in kết quả bằng printLn:

Một vấn đề với cách tiếp cận này là bạn cần biết trước độ dài của vector sẽ là bao nhiêu, vì độ dài được đưa ra như một đầu vào. Vậy nếu, thay vào đó, bạn muốn đọc chuỗi cho đến khi người dùng nhập một dòng trống? Bạn không thể biết trước người dùng sẽ nhập bao nhiêu chuỗi, vì vậy thay vào đó, bạn sẽ cần trả về độ dài cùng với một vector có độ dài đó.

5.3.2.
Reading a Vect of unknown length

Nếu bạn đọc một vector từ console, kết thúc bằng một dòng trắng, bạn không thể biết số lượng phần tử sẽ có trong vector kết quả. Trong tình huống này, bạn có thể định nghĩa một kiểu dữ liệu mới bao gồm không chỉ vector mà còn cả độ dài của nó:

data VectUnknown : Type -> Type where MkVect : (len : Nat) -> Vect len a -> VectUnknown a

Trong phát triển dựa trên kiểu, chúng ta nhằm mục đích diễn đạt những gì chúng ta biết về dữ liệu trong kiểu của nó; nếu chúng ta không thể biết điều gì đó về dữ liệu, chúng ta cũng cần phải diễn đạt điều này theo một cách nào đó. Điều này là mục đích của VectUnknown; nó chứa cả vector và chiều dài của nó, có nghĩa là chiều dài không cần phải được biết trong kiểu.

Bạn có thể xây dựng một ví dụ tại REPL:

*ReadVect> MkVect 4 ["John", "Paul", "George", "Ringo"] MkVect 4 ["John", "Paul", "George", "Ringo"] : VectUnknown String

Trên thực tế, bạn có thể để một dấu gạch dưới trong biểu thức thay vì chỉ định độ dài, 4, một cách rõ ràng, vì Idris có thể suy luận điều này từ độ dài của vector đã cho:

*ReadVect> MkVect _ ["John", "Paul", "George", "Ringo"] MkVect 4 ["John", "Paul", "George", "Ringo"] : VectUnknown String

Sau khi định nghĩa VectUnknown, thay vì viết một hàm trả về IO (Vect len String), bạn có thể viết một hàm trả về IO (VectUnknown String). Điều đó có nghĩa là nó không chỉ trả về véc tơ mà còn cả chiều dài của nó:

readVect : IO (VectUnknown String)

Loại này cho biết readVect là một chuỗi các hành động tương tác tạo ra một vectơ có độ dài không xác định, sẽ được xác định trong thời gian thực. Danh sách sau đây cho thấy một triển khai khả thi.

Listing 5.10.
Reading a `Vect` of unknown length from the console (ReadVect.idr)

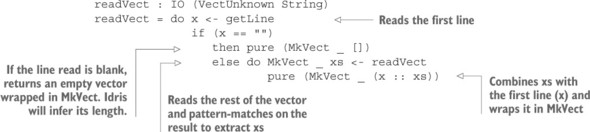
Để thử điều này, bạn có thể định nghĩa một hàm tiện ích, printVect, hiển thị nội dung và độ dài của một VectUnknown trên console:

printVect : Show a => VectUnknown a -> IO () printVect (MkVect len xs) = putStrLn (show xs ++ " (length " ++ show len ++ ")")

Sau đó, bạn có thể thử đọc một số đầu vào tại REPL:

Khi làm việc với đầu vào của người dùng, thường có một số thuộc tính của dữ liệu mà bạn không thể biết cho đến khi chạy chương trình. Độ dài của một vector là một ví dụ: khi bạn đã đọc vector, bạn biết độ dài của nó, và từ đó bạn có thể kiểm tra và lý luận về cách nó liên quan đến các dữ liệu khác. Nhưng bạn có thể gặp phải vấn đề tương tự với bất kỳ kiểu dữ liệu phụ thuộc nào được đọc từ đầu vào của người dùng, và sẽ tốt hơn nếu không định nghĩa một kiểu mới (như VectUnknown) mỗi khi điều này xảy ra. Thay vào đó, Idris cung cấp một giải pháp tổng quát hơn, đó là các cặp phụ thuộc.

5.3.3.
Dependent pairs

Bạn đã thấy tuples, được giới thiệu trong chương 2, cho phép bạn kết hợp các giá trị của các kiểu khác nhau, như trong ví dụ này:

mypair : (Int, String) mypair = (94, "Pages")

Một cặp phụ thuộc là một dạng biểu đạt phong phú hơn của cấu trúc này, trong đó kiểu của phần tử thứ hai trong một cặp có thể được tính toán từ giá trị của phần tử thứ nhất. Ví dụ:

anyVect : (n : Nat ** Vect n String) anyVect = (3 ** ["Rod", "Jane", "Freddy"])

Các cặp phụ thuộc được viết với các phần tử được phân tách bằng **. Các kiểu của chúng được viết bằng cú pháp giống như các giá trị của chúng, ngoại trừ việc phần tử đầu tiên được đặt tên rõ ràng (n trong ví dụ trước). Hình 5.5 minh họa cú pháp cho các kiểu cặp phụ thuộc.

Figure 5.5.
Dependent pair syntax. Notice that the first element is given a name that can be used in the type of the second element.

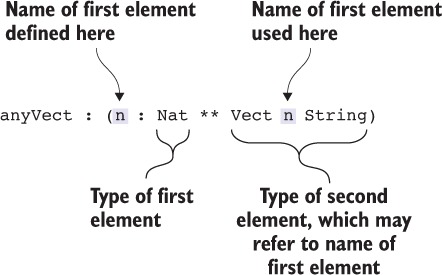
Bạn cũng thường có thể bỏ qua kiểu của phần tử đầu tiên, nếu Idris có thể suy ra nó từ kiểu của phần tử thứ hai. Ví dụ:

anyVect : (n ** Vect n String) anyVect = (3 ** ["Rod", "Jane", "Freddy"])

Nếu bạn thay thế giá trị ["Rod", "Jane", "Freddy"] bằng một lỗ trống, bạn có thể thấy cách giá trị đầu tiên, 3, ảnh hưởng đến loại của nó:

anyVect : (n ** Vect n String) anyVect = (3 ** ?anyVect_rhs)

Kiểm tra loại của ?anyVect_rhs cho thấy rằng phần tử thứ hai phải cụ thể là một vector có độ dài 3, như đã được chỉ định bởi phần tử đầu tiên:

-------------------------------------- anyVect_rhs : Vect 3 String

Types of subexpressions

Hãy nhớ rằng khi cố gắng hiểu các danh sách chương trình lớn hơn, bạn có thể thay thế các biểu thức con bằng một khoảng trống, như ?anyVect_rhs trong ví dụ suy diễn kiểu, để tìm ra các kiểu dự kiến của chúng và các kiểu của bất kỳ biến cục bộ nào đang trong phạm vi.

Thay vì định nghĩa VectUnknown như trong phần 5.3.2, bạn có thể định nghĩa một hàm đọc các vectơ có độ dài không xác định bằng cách trả về một cặp phụ thuộc gồm độ dài và một vectơ có độ dài đó. Danh sách dưới đây cho thấy cách readVect có thể được định nghĩa bằng cách sử dụng các cặp phụ thuộc.

Listing 5.11.
Reading a `Vect` of unknown length from the console, returning a dependent pair (DepPairs.idr)

Một lần nữa, bạn có thể thử điều này tại REPL. Bạn có thể sử dụng printLn để hiển thị nội dung của cặp phụ thuộc:

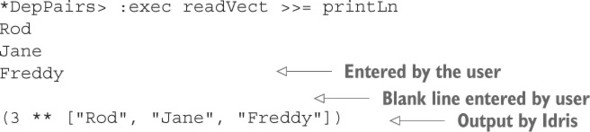
Bây giờ bạn đã có khả năng đọc các vector có độ dài tùy ý và do người dùng xác định từ bảng điều khiển, chúng ta có thể hoàn thành mục tiêu ban đầu của mình là viết một chương trình đọc hai vector và ghép chúng lại với nhau nếu độ dài của chúng khớp nhau.

5.3.4.
Validating Vect lengths

Mục tiêu của chúng tôi, như đã nêu ở đầu phần này, là viết một chương trình thực hiện các công việc sau:

Read two input vectors, using readVect.
If they have different lengths, display an error.
If they have the same lengths, display the result of zipping the vectors together.

Chương trình sẽ nhận đầu vào từ người dùng qua bảng điều khiển và hiển thị kết quả trên bảng điều khiển. Chúng tôi sẽ triển khai nó dưới dạng một hàm zipInputs, như sau:

Type— Because the input and output are entirely at the console, the type states that zipInputs takes no arguments and returns interactive actions:
```
zipInputs : IO ()
```

Define— The first step in defining the function is to read two inputs using readVect. Leave a hole, ?zipInputs_rhs, for the rest of the definition:

zipInputs : IO () zipInputs = do putStrLn "Enter first vector (blank line to end):" (len1 ** vec1) <- readVect putStrLn "Enter second vector (blank line to end):" (len2 ** vec2) <- readVect ?zipInputs_rhs

Type— Looking at the type of ?zipInputs_rhs, you can see the types (and hence the lengths) of the vectors that have been read:
```
 len2 : Nat vec2 : Vect len2 String len1 : Nat vec1 : Vect len1 String -------------------------------------- zipInputs_rhs : IO ()
```
vec1 has length len1, and vec2 has length len2; there’s no explicit relationship between these lengths. Indeed, there shouldn’t be, because they were read independently. But if you look at the type of zip, you’ll see that the lengths must be the same before you can use it:
```
zip : Vect n a -> Vect n b -> Vect n (a, b)
```
Refine— Before you can make progress, you’ll need to check that the length of the second vector is the same as the length of the first. As a first attempt, you might try the following:
```
if len1 == len2 then ?zipInputs_rhs1 else ?zipInputs_rhs2
```
Unfortunately, this doesn’t help. If you look at the type of ?zipInputs_rhs1, you’ll see that nothing has changed:
```
 len1 : Nat len2 : Nat vec2 : Vect len2 String vec1 : Vect len1 String -------------------------------------- zipInputs_rhs1 : IO ()
```
The problem is that the type of len1 == len2, Bool, tells you nothing about the meaning of the operation itself. As far as Idris is concerned, the == operation could be implemented in any way (you’ll see in chapter 7 how == can be defined) and doesn’t necessarily guarantee that len1 and len2 really are equal. Instead, you can use the following function defined in Data.Vect:
```
exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a)
```
This function takes a length, len, and a vector, input, of any length. If the length of the input vector turns out to be len, it returns Just input, with its type updated to Vect len a. Otherwise, it returns Nothing.

Implementing exactLength

Để thực hiện exactLength, bạn cần một kiểu dữ liệu biểu đạt hơn Bool để đại diện cho kết quả của một bài kiểm tra sự bằng nhau. Bạn sẽ thấy cách làm điều này trong chương 8, và chúng ta sẽ thảo luận về những hạn chế của Bool nói chung.

Using exactLength, you can refine the definition as follows:
```
zipInputs : IO () zipInputs = do putStrLn "Enter first vector (blank line to end):" (len1 ** vec1) <- readVect putStrLn "Enter second vector (blank line to end):" (len2 ** vec2) <- readVect case exactLength len1 vec2 of Nothing => ?zipInputs_rhs_1 Just vec2' => ?zipInputs_rhs_2
```

Refine— For zipInputs_rhs_1, the inputs are different lengths, so you display an error:

case exactLength len1 vec2 of Nothing => putStrLn "Vectors are different lengths" Just vec2' => ?zipInputs_rhs_2

Refine— For zipInputs_rhs_2, you have a new vector, vec2', which is the same as vec2 but with its length now guaranteed to be the same as the length of vec1, as you can confirm by looking at the type:
```
 len1 : Nat vec2' : Vect len1 String len2 : Nat vec2 : Vect len2 String vec1 : Vect len1 String -------------------------------------- zipInputs_rhs_2 : IO ()
```
You can therefore complete the definition by calling zip with vec1 and vec2', and then printing the result:
```
case exactLength len1 vec2 of Nothing => putStrLn "Vectors are different lengths" Just vec2' => printLn (zip vec1 vec2')
```

Để tham khảo, định nghĩa đầy đủ được đưa ra trong danh sách sau.

Listing 5.12.
Complete definition of `zipInputs` (DepPairs.idr)

zipInputs : IO () zipInputs = do putStrLn "Enter first vector (blank line to end):" (len1 ** vec1) <- readVect putStrLn "Enter second vector (blank line to end):" (len2 ** vec2) <- readVect case exactLength len1 vec2 of Nothing => putStrLn "Vectors are different lengths" Just vec2' => printLn (zip vec1 vec2')

Exercises

Trong các bài tập này, bạn sẽ thấy các hàm Prelude sau hữu ích, bên cạnh các hàm đã được thảo luận trước đó trong chương: openFile, closeFile, fEOF, fGetLine và writeFile. Sử dụng :doc để tìm hiểu mỗi hàm này có chức năng gì. Ngoài ra, hãy xem phần bên “Xử lý lỗi I/O.”

Write a function, readToBlank : IO (List String), that reads input from the console until the user enters a blank line.
Write a function, readAndSave : IO (), that reads input from the console until the user enters a blank line, and then reads a filename from the console and writes the input to that file.
Write a function, readVectFile : (filename : String) -> IO (n ** Vect n String), that reads the contents of a file into a dependent pair containing a length and a Vect of that length. If there are any errors, it should return an empty vector.

Handling I/O errors

Nhiều hàm trong Bài tập có thể trả về lỗi bằng cách sử dụng Either. Ban đầu, bạn có thể giả định rằng kết quả là thành công bằng cách sử dụng binding pattern-matching, như đã mô tả trong phần 5.2.2:

do Right h <- openFile filename Read Right line <- fGetLine h {- rest of code -}

Sau đó, để hoàn thiện chức năng tổng, hãy xử lý lỗi bằng cách sử dụng ký hiệu được mô tả trong cùng một phần:

do Right h <- openFile filename Read | Left err => putStrLn (show err) Right line <- fGetLine h | Left err => putStrLn (show err) {- rest of code -}

5.4. Summary

Idris provides a generic IO type for describing interactive actions.
Idris distinguishes between evaluation of pure functions and execution of interactive actions. The :exec command at the REPL executes interactive actions.
You can sequence interactive actions using do notation, which translates to applications of the >>= operator.
You can produce pure values from interactive definitions by using the pure function.
Idris provides a concise notation for pattern-matching on the result of an interactive action.
Dependent types express assumptions about inputs to functions, so you need to validate user inputs to check that they satisfy those assumptions.
Dependent pairs allow you to pair two values, where the type of the second value is computed from the first value.
You can use dependent pairs to express that a type’s argument, such as the length of a vector, will not be known until the user enters some input.

Chapter 6.
Programming with first-class types

Chương này đề cập đến

Programming with type-level functions
Writing functions with varying numbers of arguments
Using type-level functions to calculate the structure of data
Refining larger interactive programs

Trong Idris, như bạn đã thấy nhiều lần, kiểu dữ liệu có thể được thao tác giống như bất kỳ cấu trúc ngôn ngữ nào khác. Ví dụ, chúng có thể được lưu trữ trong biến, truyền cho các hàm, hoặc được xây dựng bởi các hàm. Hơn nữa, vì chúng thực sự là các loại hạng nhất, các biểu thức có thể tính toán kiểu, và kiểu cũng có thể nhận bất kỳ biểu thức nào làm tham số. Bạn đã thấy một số ứng dụng của khái niệm này trong thực tiễn, đặc biệt là khả năng lưu trữ thông tin bổ sung về dữ liệu trong kiểu của nó, chẳng hạn như độ dài của một vector.

Trong chương này, chúng ta sẽ khám phá thêm nhiều cách để tận dụng tính chất hạng nhất của các kiểu dữ liệu. Bạn sẽ thấy cách các hàm ở mức kiểu có thể được sử dụng để đặt tên thay thế cho các kiểu và cũng để tính toán kiểu của một hàm dựa trên một số dữ liệu khác. Cụ thể, bạn sẽ thấy cách bạn có thể viết một hàm xuất định dạng an toàn kiểu, printf. Đối với printf, kiểu (và thậm chí số lượng) tham số của hàm được tính toán từ một chuỗi định dạng được cung cấp là tham số đầu tiên. Kỹ thuật này, tính toán kiểu của một số dữ liệu (trong trường hợp này, các tham số của printf) dựa trên một số dữ liệu khác (trong trường hợp này, chuỗi định dạng) thường rất hữu ích. Dưới đây là một vài ví dụ:

Given an HTML form on a web page, you can calculate the type of a function to process inputs in the form.
Given a database schema, you can calculate types for queries on that database.

Là một ví dụ cho khái niệm này, bạn sẽ thấy cách sử dụng các hàm cấp loại để tinh chỉnh kho dữ liệu mà chúng ta đã triển khai vào cuối chương 4. Trước đó, bạn chỉ có thể lưu trữ dữ liệu dưới dạng Chuỗi, nhưng để linh hoạt hơn, bạn có thể muốn hình thức dữ liệu được mô tả bởi người dùng thay vì được mã hóa cứng trong chương trình. Bằng cách sử dụng các hàm cấp loại, bạn sẽ mở rộng kho dữ liệu với một sơ đồ mô tả hình thức của dữ liệu, và bạn sẽ sử dụng sơ đồ đó để tính toán các kiểu thích hợp cho các hàm phân tích và hiển thị dữ liệu người dùng. Trong quá trình này, bạn sẽ học thêm về việc sử dụng các lỗ hổng để giúp sửa lỗi khi tinh chỉnh các chương trình lớn hơn.

Để bắt đầu, chúng ta sẽ xem xét cách sử dụng hàm ở cấp độ kiểu để tính toán các kiểu.

6.1. Type-level functions: calculating types

Một trong những đặc điểm cơ bản nhất của Idris là các kiểu và biểu thức là một phần của cùng một ngôn ngữ - bạn sử dụng cùng một cú pháp cho cả hai. Bạn đã thấy trong chương 4 rằng các biểu thức có thể xuất hiện trong các kiểu. Ví dụ, trong kiểu của hàm append trên Vect, chúng ta có n và m (đều là Nats), và chiều dài kết quả là n + m:

append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Ở đây, n, m và n + m đều có kiểu Nat, mà cũng có thể được sử dụng trong các biểu thức thông thường. Tương tự, bạn có thể sử dụng kiểu trong các biểu thức và do đó viết các hàm tính toán kiểu. Có hai tình huống phổ biến mà bạn có thể muốn làm điều này:

To give more meaningful names to composite types— For example, if you have a type (Double, Double) representing a position as a 2D coordinate, you might prefer to call the type Position to make the code more readable and self-documenting.
To allow a function’s type to vary according to some contextual information— For example, the type of a value returned by a database query will vary depending on the database schema and the query itself.

Trong trường hợp đầu tiên, bạn có thể định nghĩa các đồng nghĩa kiểu, cung cấp tên thay thế cho các kiểu. Trong trường hợp thứ hai, bạn có thể định nghĩa các hàm cấp độ kiểu (mà đồng nghĩa kiểu là một trường hợp đặc biệt) tính toán các kiểu từ một số đầu vào. Trong phần này, chúng ta sẽ xem xét cả hai.

6.1.1.
Type synonyms: giving informative names to complex types

Giả sử bạn đang viết một ứng dụng liên quan đến các đa giác phức tạp, chẳng hạn như một ứng dụng vẽ. Bạn có thể đại diện cho một đa giác dưới dạng một vector của tọa độ của mỗi góc. Một hình tam giác, ví dụ, có thể được khởi tạo như sau:

tri : Vect 3 (Double, Double) tri = [(0.0, 0.0), (3.0, 0.0), (0.0, 4.0)]

Loại, Vect 3 (Double, Double) nói rõ chính xác hình thức của dữ liệu sẽ như thế nào, điều này hữu ích cho máy móc, nhưng không cung cấp bất kỳ dấu hiệu nào cho người đọc về mục đích của dữ liệu. Thay vào đó, bạn có thể tinh chỉnh loại bằng cách sử dụng một đồng nghĩa loại cho một vị trí được biểu diễn dưới dạng tọa độ 2D:

Position : Type Position = (Double, Double)

Ở đây, bạn có một hàm gọi là Position không nhận đối số và trả về một Kiểu. Đây là một hàm thông thường; không có gì đặc biệt về cách nó được khai báo hoặc thực hiện. Bây giờ, bất kỳ đâu bạn có thể sử dụng một Kiểu, bạn có thể sử dụng Position để tính toán kiểu đó. Ví dụ, tam giác có thể được định nghĩa với một kiểu tinh chỉnh như sau:

tri : Vect 3 Position tri = [(0.0, 0.0), (3.0, 0.0), (0.0, 4.0)]

Loại chức năng này là một đồng nghĩa kiểu vì nó cung cấp một tên gọi thay thế cho một loại khác.

Naming convention

Theo quy ước, chúng ta thường sử dụng chữ cái viết hoa đầu tiên cho các hàm mà nhằm mục đích tính toán kiểu.

Bởi vì chúng là các hàm thông thường, chúng cũng có thể nhận đối số. Ví dụ, danh sách dưới đây cho thấy cách bạn có thể sử dụng các từ đồng nghĩa kiểu để thể hiện rõ hơn rằng Vect được dùng để đại diện cho một đa giác.

Listing 6.1.
Defining a polygon using type synonyms (TypeSynonym.idr)

Bởi vì Polygon là một hàm thông thường, bạn có thể đánh giá nó tại REPL:

*TypeSynonyms> Polygon 3 Vect 3 (Double, Double) : Type

Ngoài ra, hãy chú ý rằng nếu bạn đánh giá tri tại REPL, Idris sẽ hiển thị kiểu của tri ở dạng đã đánh giá. Nói cách khác, việc đánh giá tại REPL sẽ đánh giá cả biểu thức và kiểu:

*TypeSynonyms> tri [(0.0, 0.0), (3.0, 0.0), (0.0, 4.0)] : Vect 3 (Double, Double)

Sử dụng :t, ngược lại, hiển thị kiểu của tri:

*TypeSynonyms> :t tri Polygon 3

Cuối cùng, bạn có thể thấy điều gì xảy ra khi bạn cố gắng định nghĩa tri một cách tương tác bằng cách sử dụng tìm kiếm biểu thức trong Atom. Nhập vào một bộ đệm Atom cái sau, cùng với định nghĩa trước đó của Đa giác:

tri : Polygon 3 tri = ?tri_rhs

Công cụ chỉnh sửa tương tác nói chung, và tìm kiếm biểu thức nói riêng, nhận thức được cách định nghĩa các từ đồng nghĩa loại, vì vậy nếu bạn thử tìm kiếm biểu thức trên tri_rhs, bạn sẽ nhận được kết quả giống như khi loại được viết trực tiếp là Vect 3 (Double, Double):

tri : Polygon 3 tri = [(?tri_rhs1, ?tri_rhs2), (?tri_rhs3, ?tri_rhs4), (?tri_rhs5, ?tri_rhs6)]

Các từ đồng nghĩa kiểu được định nghĩa trong phần này, Vị trí và Đa giác, thực chất chỉ là những hàm thông thường được sử dụng để tính toán kiểu. Điều này mang lại cho bạn nhiều linh hoạt trong cách bạn mô tả các kiểu, như bạn sẽ thấy trong phần còn lại của chương này.

6.1.2.
Type-level functions with pattern matching

Các loại đồng nghĩa là một trường hợp đặc biệt của các hàm cấp độ kiểu, là những hàm có thể được sử dụng ở bất kỳ đâu mà Idris mong đợi một Kiểu. Về mặt Idris, không có gì đặc biệt về các hàm cấp độ kiểu; chúng là những hàm thông thường mà tình cờ trả về một Kiểu, và chúng có thể sử dụng tất cả các cấu trúc ngôn ngữ có sẵn ở nơi khác. Tuy nhiên, việc xem xét chúng một cách riêng biệt là hữu ích, để hiểu cách chúng hoạt động trong thực tế.

Bởi vì các hàm cấp kiểu là các hàm thông thường trả về một kiểu, bạn có thể viết chúng bằng cách chia tách trường hợp. Ví dụ, danh sách dưới đây cho thấy một hàm tính toán một kiểu từ đầu vào Boolean. Bạn đã thấy hàm này trong chương 1, mặc dù ở một dạng hơi khác.

Listing 6.2.
A function that calculates a type from a `Bool` (TypeFuns.idr)

StringOrInt : Bool -> Type StringOrInt False = String StringOrInt True = Int

Sử dụng điều này, bạn có thể viết một hàm mà kiểu trả về được tính toán từ hoặc phụ thuộc vào một đầu vào. Sử dụng StringOrInt, bạn có thể viết các hàm trả về một trong hai kiểu, tùy thuộc vào một cờ Boolean.

Làm một ví dụ nhỏ, bạn có thể viết một hàm nhận đầu vào Boolean và trả về chuỗi "Chín mươi bốn" nếu nó là False, hoặc số nguyên 94 nếu nó là True. Bắt đầu với kiểu:

Type— Begin by giving a type declaration, using StringOrInt:

getStringOrInt : (isInt : Bool) -> StringOrInt isInt getStringOrInt isInt = ?getStringOrInt_rhs

If you look at the type of getStringOrInt_rhs now, you’ll see this:

 isInt : Bool -------------------------------------- getStringOrInt_rhs : StringOrInt isInt

Define— Because isInt appears in the required type for getStringOrInt_rhs, case splitting on isInt will cause the expected return type to change according to the specific value of isInt for each case. Case splitting on isInt leads to this:
```
getStringOrInt : (isInt : Bool) -> StringOrInt isInt getStringOrInt False = ?getStringOrInt_rhs_1 getStringOrInt True = ?getStringOrInt_rhs_2
```
Type— Looking at the types of the newly created holes, you can see how the expected type is changed in each case:
```
-------------------------------------- getStringOrInt_rhs_1 : String -------------------------------------- getStringOrInt_rhs_2 : Int
```
In getStringOrInt_rhs_1, the type is refined to StringOrInt False because the pattern for isInt is False, which evaluates to String. Then, in getString-OrInt_rhs_2, the type is refined to StringOrInt True, which evaluates to Int.

Refine— To complete the definition, you need to provide values of different types in each case:

getStringOrInt : (isInt : Bool) -> StringOrInt isInt getStringOrInt False = "Ninety four" getStringOrInt True = 94

Dependent pattern matching

Ví dụ getStringOrInt minh họa một kỹ thuật thường hữu ích khi lập trình với loại phụ thuộc: khớp kiểu phụ thuộc. Điều này đề cập đến một tình huống mà kiểu của một đối số cho một hàm có thể được xác định bằng cách kiểm tra giá trị của một đối số khác (tức là, bằng cách phân nhánh trường hợp). Bạn đã thấy một ví dụ về điều này khi định nghĩa hàm zip trong chương 4, nơi mà hình thức của một vector hạn chế các hình thức hợp lệ của vector khác, và bạn sẽ thấy nhiều hơn nữa.

Các hàm cấp độ kiểu có thể được sử dụng ở bất kỳ đâu một kiểu được mong đợi, có nghĩa là chúng có thể được sử dụng thay cho các kiểu đối số. Ví dụ, bạn có thể viết một hàm chuyển đổi một chuỗi (String) hoặc một số nguyên (Int) thành đại diện chuỗi chuẩn (canonical String), theo một cờ Boolean. Hàm này sẽ hoạt động như sau:

If the input is a String, it returns the String with leading and trailing space removed using trim.
If the input is an Int, it converts the input to a String using cast.

Documentation

Hãy nhớ rằng bạn có thể sử dụng :t và :doc để kiểm tra kiểu của những hàm mà bạn chưa quen (như trim) tại REPL.

Bạn có thể xác định chức năng này bằng các bước sau:

Type— Begin by writing a type for valToString, again using StringOrInt, but this time to calculate the input type:

valToString : (isInt : Bool) -> StringOrInt isInt -> String valToString isInt y = ?valToString_rhs

Inspecting the type of valToString_rhs, you’ll see the following:

 isInt : Bool y : StringOrInt isInt -------------------------------------- valToString_rhs : String

Define— You can define this by case splitting on isInt. The type of y is calculated from isInt, so if you case-split on isInt, you should see refined types for y in each resulting case:
```
valToString : (isInt : Bool) -> StringOrInt isInt -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2
```

Type— Inspecting the types of valToString_rhs_1 and valToString_rhs_2 shows how the type of y is refined in each case:

 y : String -------------------------------------- valToString_rhs_1 : String y : Int -------------------------------------- valToString_rhs_2 : String

Refine— To complete the definition, fill in the right side to convert y to a trimmed String if it was a String, or a string representation of the number if it was an Int:
```
valToString : (isInt : Bool) -> StringOrInt isInt -> String valToString False y = trim y valToString True y = cast y
```

Các ví dụ đơn giản trong phần này, getStringOrInt và valToString, minh họa một kỹ thuật có thể được sử dụng rộng rãi hơn trong thực tiễn. Bạn sẽ thấy một số ví dụ thực tiễn hơn ở phần sau của chương này: sử dụng một chuỗi định dạng để tính toán kiểu cho đầu ra đã định dạng, và một ví dụ lớn hơn cho phép người dùng tính toán một lược đồ, mở rộng kho dữ liệu mà bạn đã thấy ở chương 4.

Còn nhiều điều hơn bạn có thể đạt được với các biểu thức cấp kiểu. Thực tế là các kiểu là kiểu dữ liệu hạng nhất không chỉ có nghĩa là các kiểu có thể được tính toán như bất kỳ giá trị nào khác, mà còn có nghĩa là bất kỳ dạng biểu thức nào cũng có thể xuất hiện trong các kiểu.

6.1.3.
Using case expressions in types

Bất kỳ biểu thức nào có thể được sử dụng trong một hàm cũng có thể được sử dụng ở cấp độ kiểu, và ngược lại. Ví dụ, bạn có thể để lại các chỗ trống trong kiểu khi hiểu biết của bạn về các yêu cầu của hàm đang phát triển, hoặc bạn có thể sử dụng các dạng biểu thức phức tạp hơn như case. Hãy cùng xem qua cách điều này có thể hoạt động bằng cách sử dụng một biểu thức case trong kiểu của valToString thay vì một hàm StringOrInt riêng biệt.

Type— Start by giving a type for valToString, but because you don’t immediately know the input type, you can leave a hole:
```
valToString : (isInt : Bool) -> ?argType -> String
```
Define— Even though you have an incomplete type, you can still proceed with the definition by case splitting on isInt, because you at least know that isInt is a Bool:
```
valToString : (isInt : Bool) -> ?argType -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2
```
Type— Inspecting the types of valToString_rhs_1 and valToString_rhs_2 will, however, reveal that you don’t know the type of y yet:
```
 y : ?argType -------------------------------------- valToString_rhs_1 : String
```

Refine— At this stage, you need to refine the type with more details of ?argType. You can fill in ?argType with a case expression:

valToString : (isInt : Bool) -> (case _ of case_val => ?argType) -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2

Refine—
Remember that when Idris generates a case expression, it leaves an underscore in place of the value the case expression will branch on. You’ll need to fill this in before the program will compile. You can compute the argument type from the input isInt:
```
valToString : (isInt : Bool) -> (case isInt of case_val => ?argType) -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2
```

Refine— Case splitting on case_val gives you the two possible values isInt can take:

valToString : (isInt : Bool) -> (case isInt of False => ?argType_1 True => ?argType_2) -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2

You can then complete the type in the same way as your implementation of StringOrInt, refining ?argType_1 with String and ?argType_2 with Int:

valToString : (isInt : Bool) -> (case isInt of False => String True => Int) -> String valToString False y = ?valToString_rhs_1 valToString True y = ?valToString_rhs_2

Type— Inspecting ?valToString_rhs_1 and ?valToString_rhs2 now will show you the new types for the input y, calculated from the first argument:

 y : String -------------------------------------- valToString_rhs_1 : String y : Int -------------------------------------- valToString_rhs_2 : String

Refine— Finally, now that you know the type of the input y in each case, you can complete the definition as before:

valToString : (isInt : Bool) -> (case isInt of False => String True => Int) -> String valToString False y = trim y valToString True y = cast y

Totality and type-level functions

Nói chung, tốt nhất là nên xem xét các hàm cấp loại giống hệt như các hàm thông thường, như chúng ta đã làm đến nay. Tuy nhiên, không phải lúc nào cũng như vậy. Có một vài sự khác biệt kỹ thuật mà bạn nên biết:

Type-level functions exist at compile time only. There’s no runtime representation of Type, and no way to inspect a Type directly, such as pattern matching.
Only functions that are total will be evaluated at the type level. A function that isn’t total may not terminate, or may not cover all possible inputs. Therefore, to ensure that type-checking itself terminates, functions that are not total are treated as constants at the type level, and don’t evaluate further.

6.2. Defining functions with variable numbers of arguments

Bạn có thể sử dụng các hàm cấp độ kiểu để tính toán các kiểu dựa trên một số đầu vào đã biết khác. Xét rằng các kiểu hàm bản thân chúng cũng là kiểu, điều này có nghĩa là bạn có thể viết các hàm với số lượng đối số khác nhau tùy thuộc vào một số đầu vào khác. Điều này tương tự như một số ngôn ngữ khác hỗ trợ danh sách đối số có độ dài biến đổi, nhưng với độ chính xác cao hơn trong kiểu vì bạn sử dụng giá trị của một đối số để tính toán các kiểu của những đối số khác.

Trong phần này, chúng ta sẽ xem một vài ví dụ về cách điều này có thể hoạt động:

As an introductory example, we’ll write a function that adds a sequence of numbers, where the first argument is a number used to calculate the type of a function that takes that many inputs.
We’ll use the same technique to write a variant of the printf function that produces a formatted output String using a format specifier in its first argument to describe the form of later arguments.

6.2.1.
An addition function

Đầu tiên, chúng ta sẽ định nghĩa một hàm cộng, hàm này sẽ cộng lại một chuỗi số được cung cấp trực tiếp dưới dạng đối số của hàm. Hành vi của nó được đặc trưng bởi ba ví dụ được thể hiện trong hình 6.1. Một biểu thức có dạng adder numargs val sẽ tính toán một hàm nhận thêm numargs đối số, được cộng vào một giá trị khởi đầu val.

Figure 6.1.
Behavior of an addition function with a variable number of arguments

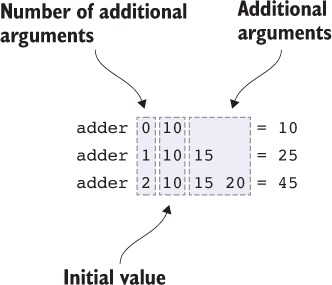
Như thường lệ trong phát triển dựa trên kiểu, bạn sẽ bắt đầu viết hàm cộng bằng cách viết kiểu của nó, nhưng trong trường hợp này, kiểu không phải là thứ bạn có thể xây dựng trực tiếp; kiểu của hàm cộng khác nhau tùy thuộc vào giá trị của đối số đầu tiên. Đối với các ví dụ được trình bày trong hình 6.1, bạn đang tìm kiếm các kiểu sau:

adder 0 : Int -> Int adder 1 : Int -> Int -> Int adder 2 : Int -> Int -> Int -> Int ...

Vì kiểu dữ liệu là hạng nhất, và kiểu này khác nhau tùy thuộc vào một số giá trị, bạn sẽ có thể tính toán nó bằng cách sử dụng một hàm cấp độ kiểu. Bạn có thể viết một hàm AdderType với hành vi cần thiết. Tên AdderType tuân theo quy ước rằng các hàm cấp độ kiểu được đặt tên bằng chữ cái đầu tiên viết hoa, và nó chỉ ra rằng nó được sử dụng để tính toán kiểu của bộ cộng.

Bạn có thể sử dụng một Nat để cung cấp độ dài của danh sách đối số, vừa vì bạn có thể tách trường hợp một cách thuận tiện, vừa vì việc có một danh sách đối số có độ dài âm là vô nghĩa. Danh sách sau đây cung cấp định nghĩa của AdderType.

Listing 6.3.
A function to calculate a type for `adder n` (Adder.idr)

Loại bộ cộng bây giờ có thể được xác định bằng cách truyền đối số đầu tiên của nó cho AdderType. Đối số thứ hai là giá trị ban đầu, mà chúng ta sẽ gọi là acc như một cách viết tắt cho "bộ tích lũy":

adder : (numargs : Nat) -> (acc : Int) -> AdderType numargs

Bởi vì bạn xác định kiểu bằng cách phân tách trường hợp dựa trên numargs trong AdderType, bạn có thể viết định nghĩa của adder với một cấu trúc tương ứng bằng cách phân tách trường hợp dựa trên numargs, để AdderType sẽ được tinh chỉnh cho mỗi trường hợp. Bạn có thể thực hiện điều này với các bước sau:

Define— Add a skeleton definition, and then case-split on the first argument:

adder : (numargs : Nat) -> (acc : Int) -> AdderType numargs adder Z acc = ?adder_rhs_1 adder (S k) acc = ?adder_rhs_2

Refine— Where the number of additional arguments, numargs, is Z, return the accumulator directly:

adder : (numargs : Nat) -> (acc : Int) -> AdderType numargs adder Z acc = acc adder (S k) acc = ?adder_rhs_2

Type— For adder_rhs_2, inspecting the type of the hole shows that you need to provide a function:
```
 k : Nat acc : Int -------------------------------------- adder_rhs_2 : Int -> AdderType k
```
This is a function type because in AdderType when numargs matches a nonzero Nat, the expected type is a function type.
Refine— The only way you have of producing something of type AdderType k in general is by calling adder with k as the first argument, so this type hints that you need to make a recursive call to adder. This is the complete definition:
```
adder : (numargs : Nat) -> (acc : Int) -> AdderType numargs adder Z acc = acc adder (S k) acc = \next => adder k (next + acc)
```

Bây giờ bạn đã có một định nghĩa đầy đủ và hoạt động, việc xem xét cách bạn có thể tinh chỉnh loại hoặc định nghĩa chính nó là một ý tưởng hay. Ví dụ, bộ cộng có thể được làm chung trong loại số mà nó cộng.

Danh sách 6.4 cho thấy một phiên bản tinh chỉnh nhẹ của hàm adder hoạt động với bất kỳ kiểu số nào, không chỉ Int. Điều này được thực hiện bằng cách truyền thêm một tham số kiểu vào AdderType, sau đó ràng buộc điều đó với các kiểu số trong kiểu của hàm adder.

Listing 6.4.
A generic adder that works for any numeric type (Adder.idr)

Hàm cộng minh họa mẫu cơ bản để định nghĩa các hàm với số lượng đối số biến đổi: bạn đã viết một hàm AdderType để tính toán loại cộng mong muốn, dựa trên một trong các đầu vào của hàm cộng. Mẫu này cũng có thể được áp dụng cho các định nghĩa lớn hơn, như bạn sẽ thấy khi chúng ta định nghĩa một hàm để định dạng đầu ra.

6.2.2.
Formatted output: a type-safe printf function

Một ví dụ lớn hơn về một hàm có số lượng đối số biến đổi là printf, được tìm thấy trong C và một số ngôn ngữ khác. Nó tạo ra đầu ra định dạng dựa trên một chuỗi định dạng và một số lượng đối số biến đổi, như được xác định bởi chuỗi định dạng. Chuỗi định dạng về cơ bản cung cấp một chuỗi mẫu để được xuất ra, được điền bởi các đối số còn lại. Về bản chất, printf có cấu trúc tổng thể giống như adder, sử dụng chuỗi định dạng để xác định loại của các đối số sau.

Hình 6.2 cho thấy một số ví dụ mô tả hành vi của printf. Lưu ý rằng thay vì xuất kết quả ra màn hình console, phiên bản printf của chúng tôi trả về một chuỗi.

Figure 6.2.
Behavior of a `printf` function with different format strings

Trong các chuỗi định dạng này, chỉ thị %d đại diện cho một số nguyên; %s đại diện cho một chuỗi; và bất kỳ thứ gì khác sẽ được in ra nguyên bản.

Theo quy trình thông thường của chúng tôi là xác định, định nghĩa và tinh chỉnh, chúng tôi sẽ bắt đầu bằng cách nghĩ về một kiểu cho printf. Giống như đối với phép cộng, chúng tôi sẽ bắt đầu với các kiểu của các ví dụ đặc trưng và sau đó tìm cách viết một hàm tính toán các kiểu này. Đây là các kiểu của các ví dụ trong hình 6.2:

printf "Hello!" : String printf "Answer: %d" : Int -> String printf "%s number %d" : String -> Int -> String

Format strings

Trong một triển khai đầy đủ của printf như được cung cấp bởi C, có nhiều chỉ thị hơn nữa ngoài %d và %s. Hơn nữa, các chỉ thị có thể được chỉnh sửa theo nhiều cách khác nhau để chỉ ra cách định dạng đầu ra (chẳng hạn như số 0 ở phía trước trong một số). Tuy nhiên, những chi tiết như vậy không làm tăng thêm gì cho cuộc thảo luận này về các hàm cấp độ kiểu, vì vậy chúng tôi sẽ bỏ qua chúng ở đây.

Để lấy kiểu của printf, bạn cần sử dụng chuỗi định dạng để xây dựng các kiểu mong đợi của các tham số. Thay vì xử lý chuỗi trực tiếp, bạn có thể viết một kiểu dữ liệu mô tả các định dạng có thể, như sau.

Listing 6.5.
Representing format strings as a data type (Printf.idr)

Điều này tạo ra sự tách biệt rõ ràng giữa việc phân tích chuỗi định dạng và việc xử lý, giống như chúng ta đã làm khi phân tích các lệnh cho kho dữ liệu trong chương 4. Ví dụ, Str (Lit " = " (Number End)) sẽ đại diện cho chuỗi định dạng "%s = %d", như được minh họa trong hình 6.3.

Figure 6.3.
Translating a format string to a `Format` description

Intermediate types

Trong quy trình phát triển dựa trên kiểu, chúng ta thường nghĩ về các hàm dưới dạng các phép biến đổi giữa các kiểu dữ liệu. Do đó, chúng ta thường định nghĩa các kiểu trung gian, chẳng hạn như Format trong phần này, để mô tả các giai đoạn trung gian của một phép toán. Có hai lý do chính cho việc này:

The meaning of String is not obvious from the type alone. The function type Format -> Type has a more precise meaning than the function type String -> Type because it’s clear that the input must be a format specification rather than any String.
Defining an intermediate data type gives us access to more interactive editing features, particularly case splitting.

Hiện tại, chúng ta sẽ làm việc trực tiếp với Format; chúng ta sẽ định nghĩa một phép chuyển đổi từ String sang Format sau. Danh sách dưới đây cho thấy cách bạn có thể tính toán kiểu của printf từ một bộ định dạng.

Listing 6.6.
Calculating the type of `printf` from a `Format` specifier (extending Printf.idr)

Danh sách 6.7 định nghĩa một hàm trợ giúp để xây dựng một chuỗi từ một định dạng, cùng với bất kỳ tham số bổ sung cần thiết nào được tính toán bởi PrintfType. Nó hoạt động giống như một hàm cộng, sử dụng một biến tích lũy để xây dựng kết quả.

Listing 6.7.
Helper function for `printf`, building a `String` from a `Format` specifier (Printf.idr)

Remember interactive editing!

Đối với các ví dụ như trong danh sách 6.6 và 6.7, đừng chỉ gõ chúng trực tiếp. Thay vào đó, hãy sử dụng các công cụ chỉnh sửa tương tác trong Atom để cố gắng tái tạo chúng một cách độc lập. Trong quá trình này, hãy chắc chắn rằng bạn xem xét các loại lỗ hổng và xem cách tìm kiếm biểu thức có thể giúp bạn đến đâu.

Cuối cùng, để triển khai một hàm printf nhận một chuỗi như một định dạng thay vì một cấu trúc Format, bạn sẽ cần có khả năng chuyển đổi một chuỗi thành một Format. Danh sách sau đây định nghĩa hàm printf cấp cao nhất thực hiện việc chuyển đổi này.

Listing 6.8.
Top-level definition of `printf`, with a conversion from `String` to `Format` (Printf.idr)

Exercises

An n x m matrix can be represented by nested vectors of Double. Define a type synonym: Matrix : Nat -> Nat -> Type. You should be able to use it to define the following matrix:
```
testMatrix : Matrix 2 3 testMatrix = [[0, 0, 0], [0, 0, 0]]
```

Extend printf to support formatting directives for Char and Double. You can test your answer at the REPL as follows:

*ex_6_2> :t printf "%c %f" printf "%c %f" : Char -> Double -> String *ex_6_2> printf "%c %f" 'X' 24 "'X' 24.0" : String

You could implement a vector as nested pairs, with the nesting calculated from the length, as in this example:
```
TupleVect 0 ty = () TupleVect 1 ty = (ty, ()) TupleVect 2 ty = (ty, (ty, ())) ...
```
Define a type-level function, TupleVect, that implements this behavior. Remember to start with the type of TupleVect. When you have the correct answer, the following definition will be valid:
```
test : TupleVect 4 Nat test = (1,2,3,4,())
```

6.3. Enhancing the interactive data store with schemas

Trong kho dữ liệu tương tác mà chúng tôi phát triển trong chương 4, bạn có thể thêm chuỗi vào kho nhớ và truy xuất chúng theo chỉ số. Nhưng nếu bạn muốn lưu trữ dữ liệu phức tạp hơn thì sao? Và nếu bạn muốn hình thức của dữ liệu được xác định bởi người dùng trước khi nhập bất kỳ dữ liệu nào, thay vì mã hóa cứng nó trong chính chương trình?

Trong phần còn lại của chương này, chúng ta sẽ mở rộng kho dữ liệu bằng cách thêm các sơ đồ để mô tả hình thức của dữ liệu. Chúng ta sẽ xác định sơ đồ dựa trên đầu vào của người dùng, và sẽ sử dụng các hàm ở mức độ kiểu để tính toán kiểu chính xác cho dữ liệu. Hình 6.4 cho thấy hai kho dữ liệu khác nhau, với các sơ đồ khác nhau, mà chúng ta sẽ có thể đại diện bằng hệ thống mở rộng của mình. Sơ đồ 1, ở trên cùng, cho thấy một kho yêu cầu dữ liệu có kiểu (Int, String), và sơ đồ 2, bên dưới, cho thấy một kho yêu cầu dữ liệu có kiểu (String, String, Int). Ngược lại, trong kho dữ liệu được phát triển trong chương 4, sơ đồ thực tế luôn là String.

Figure 6.4.
Two different data stores, with different schemas. Schema 1 requires the data to be of type `(Int, String)`, and schema 2 requires the data to be of type `(String, String, Int)`

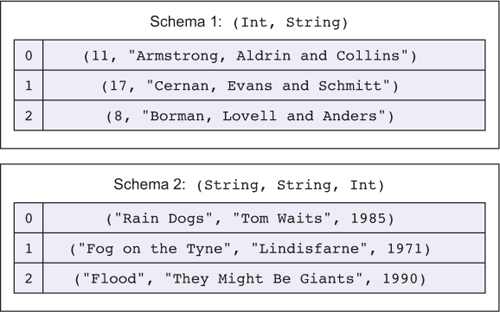
Một tương tác điển hình với hệ thống mở rộng có thể diễn ra như sau. Lưu ý rằng chúng tôi đang mô tả sơ đồ trước khi nhập bất kỳ dữ liệu nào.

Command: schema String String Int OK Command: add "Rain Dogs" "Tom Waits" 1985 ID 0 Command: add "Fog on the Tyne" "Lindisfarne" 1971 ID 1 Command: get 1 "Fog on the Tyne", "Lindisfarne", 1971 Command: quit

Thay vì bắt đầu từ đầu, chúng ta sẽ bắt đầu với kho dữ liệu hiện có mà chúng ta đã triển khai trong chương 4 và tinh chỉnh hệ thống tổng thể khi cần thiết. Chúng ta sẽ áp dụng cách tiếp cận này:

Refine the representation of DataStore to include schema descriptions. This refinement will inevitably mean that our program no longer type-checks.
Correct any errors, introducing holes for any more-complex errors.
Fill in the holes to complete the implementation, and add any further features that are now supported as a result of refining the type.

6.3.1.
Refining the DataStore type

Hiện tại, DataStore chỉ hỗ trợ lưu trữ Chuỗi. Chúng tôi đã triển khai nó trong chương 4 với loại sau:

data DataStore : Type where MkData : (size : Nat) -> (items : Vect size String) -> DataStore

Thay vì sử dụng một chuỗi kích thước Vect cho các mặt hàng trong cửa hàng, chúng tôi muốn linh hoạt hơn về các loại mặt hàng này. Một cách tự nhiên để làm điều này có thể là tinh chỉnh điều này thành một phiên bản tổng quát của DataStore, tham số hóa nó dựa trên một sơ đồ cho biết loại dữ liệu trong cửa hàng:

data DataStore : Type -> Type where MkData : (size : Nat) -> (items : Vect size schema) -> DataStore schema

Commenting out code sections

Trong khi bạn làm việc trên DataStore đã được tinh chỉnh, bạn sẽ không tránh khỏi việc làm hỏng phần còn lại của chương trình, khiến nó không còn kiểm tra kiểu nữa. Vì vậy, tôi gợi ý bạn nên chú thích phần còn lại của mã (đặt nó giữa {- và -}) cho đến khi bạn hoàn thành kiểu DataStore mới và sẵn sàng để tiếp tục.

Chúng tôi muốn người dùng có thể mô tả và có thể cập nhật được sơ đồ, nhưng nếu chúng tôi tham số hóa theo một loại sơ đồ, sơ đồ sẽ bị cố định trong kiểu. Thay vào đó, chúng tôi sẽ tạo ra một loại dữ liệu để mô tả các sơ đồ, và một hàm cấp độ kiểu để chuyển đổi các mô tả sơ đồ (có thể được cung cấp bởi người dùng trong thời gian chạy) thành các loại cụ thể. Danh sách sau đây cho thấy một phác thảo về loại DataStore được tinh chỉnh.

Listing 6.9.
Outline of the refined `DataStore` type, with the `Schema` description and the translation of `Schema` to concrete types left undefined (DataStore.idr)

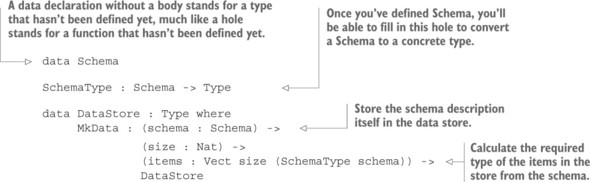
Chúng tôi sẽ định nghĩa Schema là sự kết hợp của String và Int, theo một định nghĩa do người dùng cung cấp. Người dùng sẽ cung cấp một Schema, và chúng tôi sẽ chuyển đổi Schema thành một kiểu cụ thể bằng cách sử dụng một hàm cấp loại, SchemaType.

Danh sách tiếp theo cho thấy cách bạn có thể mô tả Các Lược Đồ và chuyển chúng thành Các Kiểu Idris bằng cách sử dụng một hàm cấp kiểu, SchemaType.

Listing 6.10.
Defining `Schema`, and converting a `Schema` to a concrete type

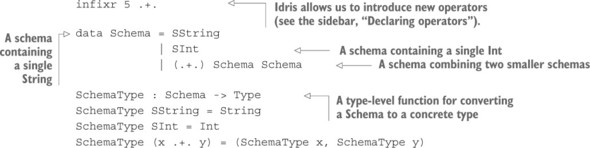
Bạn có thể thử điều này để định nghĩa các lược đồ cho hai cửa hàng ví dụ được trình bày trong hình 6.4 trước đó:

*DataStore> SchemaType (SInt .+. SString) (Int, String) : Type *DataStore> SchemaType (SString .+. SString .+. SInt) (String, String, Int) : Type

Declaring operators

Bạn có thể định nghĩa các toán tử mới bằng cách chỉ định độ cố định và độ ưu tiên của chúng. Trong danh sách 6.10, bạn đã có điều này:

infixr 5 .+.

Điều này giới thiệu một toán tử vị trí giữa phải liên kết mới (infixr) với mức độ ưu tiên 5. Nói chung, các toán tử được giới thiệu với từ khóa infixl (cho các toán tử liên kết trái), infixr (cho các toán tử liên kết phải) hoặc infix (cho các toán tử không liên kết), theo sau là một mức độ ưu tiên và một danh sách các toán tử.

Thậm chí các toán tử số học và so sánh cũng được định nghĩa theo cách này, thay vì là cú pháp tích hợp sẵn. Chúng được giới thiệu như sau trong Prelude:

infixl 5 ==, /= infixl 6 <, <=, >, >= infixl 7 <<, >> infixl 8 +, - infixl 9 *, /

Toán tử :: và ++ trên danh sách cũng được định nghĩa trong Prelude và được khai báo như sau:

infixr 7 ::, ++

Loại DataStore mới cho phép bạn lưu trữ không chỉ kích thước và nội dung của store, mà còn cả mô tả về cấu trúc của nội dung store dưới dạng một sơ đồ. Trước đây, mỗi mục luôn là một Chuỗi, nhưng bây giờ dạng thức được xác định bởi người dùng.

Bây giờ, vì bạn đã thay đổi định nghĩa của DataStore, bạn cũng sẽ cần phải thay đổi các hàm truy cập nó.

6.3.2.
Using a record for the DataStore

Để có thể sử dụng loại DataStore đã được cập nhật, bạn sẽ cần định nghĩa lại các hàm size và items để chiếu các trường liên quan ra khỏi cấu trúc.

Định nghĩa kích thước tương tự như định nghĩa trước đó:

size : DataStore -> Nat size (MkData schema' size' items') = size'

Để xác định các mục, tuy nhiên, bạn cũng cần viết một hàm để chiếu một lược đồ từ cửa hàng, vì bạn cần biết mô tả lược đồ để biết loại của các mục trong cửa hàng.

schema : DataStore -> Schema schema (MkData schema' size' items') = schema' items : (store : DataStore) -> Vect (size store) (SchemaType (schema store)) items (MkData schema' size' items') = items'

Việc viết các hàm chiếu như thế này, về cơ bản là trích xuất các trường từ các bản ghi, có thể trở nên nhàm chán rất nhanh chóng. Thay vào đó, Idris cung cấp một cú pháp để định nghĩa các bản ghi, dẫn đến việc tự động sinh ra các hàm để chiếu các trường từ một bản ghi. Bạn có thể định nghĩa DataStore như sau.

Listing 6.11.
Implementing `DataStore` as a record, with automatically generated projection functions

Một khai báo bản ghi giới thiệu một kiểu dữ liệu mới, giống như một khai báo dữ liệu, nhưng có hai điểm khác biệt:

There can be only one constructor.
The fields give rise to projection functions, automatically generated from the types of the fields.

Trong trường hợp của DataStore, bạn có thể thấy các loại của bộ xây dựng dữ liệu MkData và các hàm chiếu được tạo ra từ các trường bằng cách sử dụng :doc:

*DataStore> :doc DataStore Record DataStore Constructor: MkData : (schema : Schema) -> (size : Nat) -> (items : Vect size (SchemaType schema)) -> DataStore Projections: schema : (rec : DataStore) -> Schema size : (rec : DataStore) -> Nat items : (rec : DataStore) -> Vect (size rec) (SchemaType (schema rec))

Bạn có thể thử điều này bằng cách tạo một bản ghi thử nghiệm đơn giản tại REPL:

*DataStore> :let teststore = (MkData (SString .+. SInt) 1 [("Answer", 42)]) *DataStore> :t teststore teststore : DataStore

Tiếp theo, bạn có thể dự đoán schema, kích thước và danh sách các mục từ bản ghi thử nghiệm này:

*DataStore> schema teststore SString .+. SInt : Schema *DataStore> size teststore 1 : Nat *DataStore> items teststore [("Answer", 42)] : Vect 1 (String, Int)

Các bản ghi thực ra linh hoạt hơn nhiều so với những gì có thể thấy trong ví dụ nhỏ này. Cũng như việc chiếu ra các giá trị của các trường, Idris cung cấp cú pháp cho việc thiết lập các trường và cập nhật các bản ghi. Bạn sẽ tìm hiểu thêm về các bản ghi khi chúng ta thảo luận về việc làm việc với trạng thái trong chương 12.

6.3.3.
Correcting compilation errors using holes

Bây giờ mà bạn có một định nghĩa mới về DataStore, chương trình cũ của bạn sử dụng nó sẽ không còn kiểm tra kiểu đúng nữa vì nó phụ thuộc vào định nghĩa cũ. Bước tiếp theo trong việc tinh chỉnh chương trình kho dữ liệu của bạn là cập nhật các định nghĩa để toàn bộ chương trình lại có thể kiểm tra kiểu. Điều này không nhất thiết có nghĩa là hoàn thành chương trình; ở giai đoạn này, việc giải quyết các lỗi kiểu bằng cách chèn các khoảng trống mà bạn sẽ điền sau là hoàn toàn ổn.

Trước đây, tôi đã đề xuất tạm thời bình luận (comment out) đoạn mã sau định nghĩa của DataStore để bạn có thể làm việc với định nghĩa tinh chỉnh mà không lo lắng về lỗi biên dịch. Bây giờ, chúng ta sẽ làm việc qua phần còn lại của chương trình, từng bước bỏ bình luận các định nghĩa và sửa chữa chúng, dựa vào các lỗi kiểu mà Idris cung cấp cho chúng ta.

Đầu tiên, hãy bỏ chú thích addToStore, được định nghĩa trước đó như sau:

addToStore : DataStore -> String -> DataStore addToStore (MkData size store) newitem = MkData _ (addToData store) where addToData : Vect oldsize String -> Vect (S oldsize) String addToData [] = [newitem] addToData (item :: items) = item :: addToData items

Khi tải lại, bằng cách sử dụng Ctrl-Alt-R trong Atom hoặc lệnh :r tại REPL, Idris báo cáo như sau:

DataStore.idr:21:1-11: When checking left hand side of addToStore: When checking an application of Main.addToStore: Type mismatch between Vect size (SchemaType schema) -> DataStore (Type of MkData schema size) and DataStore (Expected type)

Vấn đề đầu tiên ở đây là bạn đã thêm một đối số vào MkData; giờ đây nó yêu cầu một schema cũng như kích thước và một vector các mục. Bạn có thể sửa lại điều này bằng cách thêm một đối số schema vào MkData:

addToStore : DataStore -> String -> DataStore addToStore (MkData schema size store) newitem = MkData schema _ (addToData store) where addToData : Vect oldsize String -> Vect (S oldsize) String addToData [] = [newitem] addToData (item :: items) = item :: addToData items

Idris hiện báo cáo

Type mismatch between Vect size (SchemaType schema) (Type of store) and Vect size String (Expected type)

Vấn đề là kho dữ liệu không còn chỉ lưu trữ chuỗi nữa, mà lưu trữ một loại được mô tả bởi lược đồ. Bạn có thể sửa điều này bằng cách thay đổi các kiểu của addToStore và addToData sao cho chúng hoạt động với kiểu chính xác. Một định nghĩa đúng kiểu của addToStore được hiển thị trong danh sách sau.

Listing 6.12.
A corrected definition of `addToStore` using the refined `DataStore` type

Nếu bạn tiếp tục bỏ chú thích các định nghĩa một cách lần lượt, lỗi tiếp theo bạn sẽ gặp phải là ở getEntry. Hiện tại nó được định nghĩa như sau, với dòng sai được đánh dấu.

Listing 6.13.
Old version of `getEntry`, with an error in the application of `index`

Vấn đề nằm ở dòng cuối cùng, nơi bạn lấy một mục từ kho, vì bạn đang đối xử với kho như một Vect chứa các Chuỗi. Đây là những gì Idris báo cáo:

When checking an application of function Data.Vect.index: Type mismatch between Vect (size store) (SchemaType (schema store)) (Type of items store) and Vect (size store) String (Expected type)

Vấn đề nằm ở việc áp dụng chỉ mục, không còn trả về một chuỗi. Bạn có thể chỉnh sửa lỗi này tạm thời bằng cách chèn một khoảng trống để chuyển đổi kết quả của chỉ mục thành một chuỗi, như sau.

Listing 6.14.
Correcting `getEntry` by inserting a hole to convert the contents of the store to a displayable `String`

Nếu bạn kiểm tra loại hiển thị, bạn sẽ thấy loại chức năng bạn cần để lấp đầy chỗ trống, chuyển đổi một SchemaType (lưu trữ sơ đồ) thành một String:

 store : DataStore id : Fin (size store) pos : Integer store_items : Vect (size store) (SchemaType (schema store)) -------------------------------------- display : SchemaType (schema store) -> String

Chúng tôi sẽ trở lại với ?display sớm thôi. Hiện tại, hãy kiểm tra kiểu getEntry một lần nữa. Lỗi tiếp theo nằm trong processInput. Đây là định nghĩa hiện tại.

Listing 6.15.
Old version of `processInput`, with an error in the application of `addToStore`

Định nghĩa này có một lỗi tương tự như getEntry, cho thấy bạn có một String nhưng Idris đã mong đợi một SchemaType (lưu trữ schema):

When checking an application of function Main.addToStore: Type mismatch between String (Type of item) and SchemaType (schema store) (Expected type)

Một cách sửa chữa có thể là, giống như với getEntry, thêm một lỗ hổng để chuyển đổi chuỗi thành SchemaType thích hợp (lưu trữ lược đồ) trong processInput:

Just ("ID " ++ show (size store) ++ "\n", addToStore store (?convert item))

Ngoài ra, bạn có thể tinh chỉnh định nghĩa của Command sao cho nó chỉ đại diện cho các lệnh hợp lệ, nghĩa là bất kỳ đầu vào nào của người dùng không hợp lệ sẽ dẫn đến lỗi phân tích cú pháp. Chúng tôi sẽ chọn cách tiếp cận này, vì nó liên quan đến việc định nghĩa một kiểu trung gian chính xác hơn, để bạn có thể kiểm tra tính hợp lệ của đầu vào càng sớm càng tốt.

Để đạt được điều này, hãy tham số hóa Command bằng mô tả lược đồ, và thay đổi lệnh Add sao cho nó nhận một SchemaType thay vì đầu vào String trực tiếp. Dưới đây là định nghĩa tinh chỉnh của Command.

Listing 6.16.
`Command`, refined to be parameterized by the `schema` in the data store

Bạn bây giờ có thể thay đổi hàm parse để nhận một mô tả sơ đồ rõ ràng, và thêm một chỗ trống ở những nơi cần thiết để chuyển đổi đầu vào kiểu String thành kiểu SchemaType. Một định nghĩa mới của hàm parse mà kiểm tra kiểu là như sau.

Listing 6.17.
Updating `parseCommand` so that it parses inputs that conform to the schema

Lỗ kết quả có một loại giải thích rằng nó chuyển đổi một chuỗi thành một thể hiện thích hợp của kiểu sơ đồ SchemaType.

 schema : Schema rest : String -------------------------------------- parseBySchema : String -> SchemaType schema

Tuy nhiên, vẫn còn một vấn đề ở đây! Hàm này không thể tổng quát vì không phải mọi chuỗi đều có thể phân tích cú pháp thành một thể hiện hợp lệ của lược đồ. Tuy nhiên, mục tiêu của bạn lúc này chỉ đơn giản là làm cho chương trình tổng thể kiểm tra kiểu một lần nữa. Chúng ta sẽ trở lại vấn đề này sớm thôi.

Bạn đã tinh chỉnh loại lệnh, thêm tham số schema vào parse, và chèn các khoảng trống để hiển thị các mục (?display) và chuyển đổi đầu vào của người dùng thành các mục (?parseBySchema). Tất cả những gì còn lại là cập nhật processInput và main để sử dụng các định nghĩa mới. Đây là những thay đổi nhỏ, được trình bày trong danh sách tiếp theo. Trong processInput, bạn truyền schema hiện tại cho parse, và trong main, bạn đặt schema ban đầu để chỉ chấp nhận các chuỗi.

Listing 6.18.
Updated `processInput` and `main`, with a default schema

Để tổng hợp lại, bạn đã cập nhật loại DataStore để cho phép các sơ đồ do người dùng định nghĩa, định nghĩa nó bằng cách sử dụng một bản ghi để tự động có các hàm truy cập trường, và bạn đã cập nhật phần còn lại của chương trình để nó giờ đây có thể kiểm tra kiểu, tạm thời insert các lỗ hổng cho những phần khó sửa chữa ngay lập tức.

6.3.4.
Displaying entries in the store

Bạn hiện có hai lỗ cần điền trước khi có thể thực thi chương trình này. Lỗ đầu tiên là ?display, chuyển đổi một mục trong kho thành một chuỗi, trong đó lược đồ trong kho cho biết dạng của dữ liệu:

 store : DataStore id : Fin (size store) pos : Integer store_items : Vect (size store) (SchemaType (schema store)) -------------------------------------- display : SchemaType (schema store) -> String

Trong trường hợp này, việc sử dụng Ctrl-Alt-L để nâng lỗ hổng lên một hàm cấp cao sẽ cung cấp cho bạn nhiều thông tin mà bạn không cần để triển khai hiển thị. Tất cả những gì bạn thực sự cần là một mô tả lược đồ và dữ liệu.

Thay vào đó, bạn có thể triển khai hiển thị bằng tay như sau:

Type— First, you can write a more generic type than Idris suggested. Rather than specifically using a schema extracted from a store, you can display data according to any schema:
```
display : SchemaType schema -> String
```
Define— In order to define this function, you need to know about the schema itself. Otherwise, you won’t know what form the data is in. Add a skeleton definition, and then bring the implicit argument schema into scope:
```
display : SchemaType schema -> String display {schema} item = ?display_rhs
```
Define—
You can define the function by case splitting on schema. Because the type of item is SchemaType schema, case splitting on schema will give you more information about the expected type of item:
```
display : SchemaType schema -> String display {schema = SString} item = ?display_rhs_1 display {schema = SInt} item = ?display_rhs_2 display {schema = (x .+. y)} item = ?display_rhs_3
```

Type— Inspecting each of the resulting holes (?display_rhs_1, ?display_rhs_2 and ?display_rhs_3) tells you what item must be in each case:

 item : String -------------------------------------- display_rhs_1 : String item : Int -------------------------------------- display_rhs_2 : String x : Schema y : Schema item : (SchemaType x, SchemaType y) -------------------------------------- display_rhs_3 : String

Refine— For ?display_rhs_1 and ?display_rhs_2 you can complete the definition by directly converting item to a String. For ?display_rhs_3, you can case-split on item and recursively display each entry:

display : SchemaType schema -> String display {schema = SString} item = show item display {schema = SInt} item = show item display {schema = (x .+. y)} (iteml, itemr) = display iteml ++ ", " ++ display itemr

Khi định nghĩa này hoàn tất và tệp được tải lại vào Idris REPL, sẽ còn lại một lỗ hổng, ?parseBySchema.

6.3.5.
Parsing entries according to the schema

Lỗ hổng còn lại, ?parseBySchema, được dùng để chuyển đổi chuỗi mà người dùng nhập vào thành loại phù hợp với schema. Bạn có thể xem điều gì được mong đợi bằng cách xem kiểu của nó:

 rest : String schema : Schema -------------------------------------- parseBySchema : String -> SchemaType schema

Như bạn đã thấy trước đó, không phải mọi chuỗi đều dẫn đến một lược đồ SchemaType hợp lệ, vì vậy bạn có thể tinh chỉnh loại này một chút và tạo ra một hàm cấp cao trả về Maybe (SchemaType schema) để phản ánh thực tế rằng việc phân tích đầu vào có thể thất bại, đồng thời làm cho lược đồ trở nên rõ ràng.

parseBySchema : (schema : Schema) -> String -> Maybe (SchemaType schema)

Sau đó, bạn có thể chỉnh sửa parseCommand để sử dụng hàm mới này. Nếu parseBySchema thất bại (tức là trả về Nothing), parseCommand cũng nên trả về Nothing.

parseCommand schema "add" rest = case parseBySchema schema rest of Nothing => Nothing Just restok => Just (Add restok)

Để phân tích cú pháp các đầu vào hoàn chỉnh như mô tả bởi các schema, bạn sẽ cần có khả năng phân tích cú pháp các phần của đầu vào theo một tập hợp con của schema. Ví dụ, given một schema (SInt .+. SString) và một đầu vào 100 "Antelopes", bạn sẽ cần có khả năng phân tích cú pháp tiền tố 100 dưới dạng SInt, tiếp theo là phần còn lại, "Antelopes", dưới dạng SString.

Bạn có thể định nghĩa bộ phân tích cú pháp của mình với hai thành phần sau:

parsePrefix reads a prefix of the input according to the schema and returns the parsed input, if successful, paired with the remainder of the text.
parseBySchema calls parsePrefix with some input and ensures that once it has parsed the input according to the schema, there’s no input remaining.

Danh sách tiếp theo cho thấy triển khai cấp cao của parseBySchema và kiểu của hàm trợ giúp parsePrefix.

Listing 6.19.
Outline implementation of `parseBySchema`, using an undefined `parsePrefix` function to parse a prefix of an input according to a schema

Hãy cùng xem qua sơ đồ của parsePrefix, theo phương pháp xác định-định nghĩa-rà soát và xem cấu trúc của lược đồ cung cấp cho chúng ta những gợi ý như thế nào về cách tiến hành từng phần của việc thực hiện:

Define— You already have the type, so begin by providing a skeleton definition:

parsePrefix : (schema : Schema) -> String -> Maybe (SchemaType schema, String) parsePrefix schema item = ?parsePrefix_rhs

Define— If you case-split on schema, Idris will generate cases for each possible form of the schema:

parsePrefix : (schema : Schema) -> String -> Maybe (SchemaType schema, String) parsePrefix SString input = ?parsePrefix_rhs_1 parsePrefix SInt input = ?parsePrefix_rhs_2 parsePrefix (x .+. y) input = ?parsePrefix_rhs_3

Type— Looking at the types of the holes tells you what the return types must be for each form of the schema. For example, in ?parsePrefix_rhs_2 you need to convert the input into a Int, if possible, paired with the rest of the input:
```
 input : String -------------------------------------- parsePrefix_rhs_2 : Maybe (Int, String)
```
Refine— For ?parsePrefix_rhs_2, if the prefix of the input contains digits, you can convert them to an Int and return the resulting Int and the remainder of the String. You can refine it to the following:
```
parsePrefix SInt input = case span isDigit input of ("", rest) => Nothing (num, rest) => Just (cast num, ltrim rest)
```
If the prefix of the input that contains digits is empty, then it’s not a valid Int, so return Nothing. Otherwise, you can convert the prefix to an Int and return the rest of the input, with leading spaces trimmed using ltrim.
Refine— You can refine ?parsePrefix_rhs_1 similarly, looking for an opening quotation mark and then reading the string until you reach the closing quotation mark. You’ll see the complete definition shortly in listing 6.20.
Refine— The type of ?parsePrefix_rhs_3 shows that you need to parse two subschemas and combine the results:
```
 x : Schema y : Schema input : String -------------------------------------- parsePrefix_rhs_3 : Maybe ((SchemaType x, SchemaType y), String)
```
It’s a good idea to give x and y more-meaningful names before proceeding:
```
parsePrefix (schemal .+. schemar) input = ?parsePrefix_rhs_3
```
To refine parsePrefix_rhs_3, you can recursively parse the first portion of the input according to schemal, and if that succeeds, parse the rest of the input according to schemar. Parse the first portion:
```
parsePrefix (schemal .+. schemar) input = case parsePrefix schemal input of Nothing => Nothing Just (l_val, input') => ?parsePrefix_rhs_2
```
If parsePrefix on the first part of the schema fails, the whole thing will fail. Otherwise, you have a new hole:
```
 schemal : Schema l_val : SchemaType schemal input' : String schemar : Schema input : String -------------------------------------- parsePrefix_rhs_2 : Maybe ((SchemaType schemal, SchemaType schemar), String)
```
Keep reloading!

Trong khi theo đuổi cách tiếp cận dựa trên kiểu dữ liệu này, bạn luôn có một tệp mà được kiểm tra kiểu càng nhiều càng tốt. Ở đây, thay vì lấp kín lỗ hổng hoàn toàn, bạn đã viết một phần nhỏ của nó với một lỗ hổng mới và kiểm tra rằng những gì bạn có được kiểm tra kiểu trước khi tiến hành.
Refine— Finally, you can complete this case by parsing the remaining input according to schemar:
```
parsePrefix (schemal .+. schemar) input = case parsePrefix schemal input of Nothing => Nothing Just (l_val, input') => case parsePrefix schemar input' of Nothing => Nothing Just (r_val, input'') => Just ((l_val, r_val), input'')
```
Nested case blocks

Những khối lệnh điều kiện lồng nhau mà chúng tôi đã sử dụng có vẻ hơi dài dòng. Trong phần 6.3.7, bạn sẽ thấy một cách để viết chúng ngắn gọn hơn.

Danh sách sau đây cho thấy triển khai hoàn chỉnh của parsePrefix, bổ sung các chi tiết còn lại, bao gồm việc phân tích chuỗi có dấu nháy. Bây giờ bạn đã có một triển khai hoàn chỉnh có thể biên dịch và chạy.

Listing 6.20.
Parsing a prefix of an input according to a specific `schema`

6.3.6.
Updating the schema

Mặc dù bạn đã có một triển khai hoàn chỉnh, nó vẫn không có chức năng gì hơn phiên bản trước, vì sơ đồ được khởi tạo là SString trong hàm main, và bạn chưa thực hiện cách nào để cập nhật điều này.

main : IO () main = replWith (MkData SString _ []) "Command: " processInput

Bạn có thể, ít nhất, thử nghiệm với các sơ đồ khác bằng cách cập nhật main và biên dịch lại. Ví dụ, bạn có thể thử một sơ đồ chấp nhận hai chuỗi và một số nguyên:

main : IO () main = replWith (MkData (SString .+. SString .+. SInt) _ []) "Command: " processInput

Bạn có thể biên dịch và chạy điều này bằng cách sử dụng :exec tại REPL, và thử một vài mục ví dụ:

*DataStore> :exec Command: add "Bob Dylan" "Blonde on Blonde" 1965 ID 0 Command: add "Prefab Sprout" "From Langley Park to Memphis" 1988 ID 1 Command: get 0 "Bob Dylan", "Blonde on Blonde", 1965

Tuy nhiên, sẽ tốt hơn nếu cho phép người dùng định nghĩa các sơ đồ của riêng họ, thay vì cố định chúng vào phần chính. Để đạt được điều này, bạn có thể thêm một lệnh mới để thiết lập một sơ đồ mới, cập nhật kiểu dữ liệu Command.

Listing 6.21.
The `Command` data structure with a new command for updating the schema

Bạn cũng sẽ cần các hàm để thực hiện các điều sau đây:

Update the DataStore type to hold the new schema. This should only work when the store is empty, because when you change the schema type, it invalidates the current contents of the store.
Parse a schema description from user input.

Bạn cũng sẽ cần cập nhật parseCommand và processInput để xử lý việc phân tích và xử lý lệnh mới. Những hàm mới này được triển khai theo cùng một quy trình mà bạn đã làm cho đến nay trong việc triển khai kho dữ liệu mở rộng. Danh sách 6.22 cho thấy cách phân tích lệnh mới hoạt động. Nó thêm một lệnh người dùng, schema, theo sau là một danh sách các String và Int, và chuyển đổi điều này thành lệnh SetSchema.

Listing 6.22.
Parsing a `Schema` description, and extending the parser for `Command` to support setting a new schema

Danh sách 6.23 cho thấy cách cập nhật lược đồ hoạt động một khi lệnh mới đã được phân tích. Như một lựa chọn thiết kế, nó chỉ cho phép lược đồ được cập nhật khi kho dữ liệu rỗng, vì không có cách chung nào để cập nhật nội dung của kho dữ liệu với một lược đồ được cập nhật tùy ý (một lựa chọn khác là làm rỗng kho dữ liệu khi người dùng thay đổi lược đồ).

Listing 6.23.
Processing the `SetSchema` command, updating the schema description in the `DataStore`

Cuối cùng, bạn có thể biên dịch và chạy chương trình này và thử đặt một schema mới từ đầu vào của người dùng:

*DataStore> :exec Command: schema Int String OK Command: add 99 "Red balloons" ID 0 Command: add 76 "Trombones" ID 1 Command: schema String String Int Can't update schema when entries in store Command: get 1 76, "Trombones"

Cuối cùng, việc sử dụng một kiểu dữ liệu để mô tả lược đồ và sử dụng lược đồ đó để tính toán các kiểu của các thao tác trên kho dữ liệu có một số hệ quả:

On reading user input, you can’t add the input to the store if it’s not valid according to the schema.
If you change the schema type, you can’t invalidate the contents of the store because the type of the store’s contents prevents it. Changing the schema type requires you to have an empty store.
When writing the parser for user input, you can use the description of the schema to guide the implementation of the parser and to build the correct type for the input.

6.3.7.
Sequencing expressions with Maybe using do notation

Trong chương trình lưu trữ dữ liệu, có vài nơi chúng tôi đã sử dụng khối case để kiểm tra kết quả của một hàm trả về giá trị kiểu Maybe, và đã chuyển kết quả đó đi. Ví dụ:

parseCommand schema "schema" rest = case parseSchema (words rest) of Nothing => Nothing Just schemaok => Just (SetSchema schemaok)

Ở đây, parseCommand, trả về một thứ thuộc loại Maybe (Command schema), đã gọi parseSchema, cái mà trả về một thứ thuộc loại Maybe Schema, và đã sử dụng một biểu thức case để kiểm tra kết quả của cuộc gọi tới parseSchema.

Nếu parseSchema thất bại, parseCommand cũng thất bại. Tương tự, nếu parseSchema thành công, thì parseCommand cũng thành công.

Bạn có thể thấy một mô hình tương tự trong hàm maybeAdd trong danh sách dưới đây, hàm này cộng hai giá trị có kiểu Maybe Int, trả về Nothing nếu một trong hai đầu vào là Nothing.

Listing 6.24.
Adding two `Maybe Ints` (Maybe.idr)

Bạn có thể thử maybeAdd trên một vài ví dụ, và bạn sẽ thấy rằng nó thêm các đầu vào của nó nếu cả hai đều có dạng Just val cho một giá trị cụ thể val nào đó, và nó sẽ trả về Nothing nếu một trong hai đầu vào là Nothing:

*Maybe> maybeAdd (Just 3) (Just 4) Just 7 : Maybe Int *Maybe> maybeAdd (Just 3) Nothing Nothing : Maybe Int *Maybe> maybeAdd Nothing (Just 4) Nothing : Maybe Int

Một mẫu phổ biến được tìm thấy ở đây, trong parseCommand, và ở một số nơi khác trong việc triển khai lưu trữ dữ liệu:

Evaluate an expression of type Maybe ty. The result is either Nothing or Just x, where x has type ty.
If the result is Nothing, the result of the entire computation is Nothing.
If the result is Just x, pass x to the rest of the computation.

Khi bạn thấy một mẫu chung, thật tốt khi cố gắng nắm bắt mẫu đó trong một hàm bậc cao. Thực tế, bạn đã thấy một toán tử thực hiện một mẫu tương tự trong chương 5, khi tuần tự hóa các thao tác IO.

(>>=) : IO a -> (a -> IO b) -> IO b

Cùng một toán tử hoạt động cho việc sắp xếp các phép toán Maybe, khi được định nghĩa như sau:

(>>=) : Maybe a -> (a -> Maybe b) -> Maybe b (>>=) Nothing next = Nothing (>>=) (Just x) next = next x

Hiệu quả, nó lấy đầu ra của phép toán đầu tiên, nếu thành công (nghĩa là, trả về một Just), và truyền nó làm đầu vào cho phép toán thứ hai. Nó nắm bắt một mẫu phổ biến trong việc đánh giá một biểu thức với kiểu Maybe.

Type of (>>=)

Nhớ từ chương 5 rằng nếu bạn kiểm tra kiểu của (>>=) tại REPL, bạn sẽ thấy một kiểu tổng quát bị ràng buộc:

Idris> :t (>>=) (>>=) : Monad m => m a -> (a -> m b) -> m b

Nói chung, toán tử >>= có thể được sử dụng để tuần tự hóa các phép tính. Bạn sẽ thấy cách điều này hoạt động trong chương 7 khi chúng ta bàn về các giao diện.

Sử dụng (>>=) như một toán tử ở giữa, bạn có thể viết lại maybeAdd một cách ngắn gọn hơn, mặc dù có phần khó hiểu, như trong danh sách sau.

Listing 6.25.
Adding two `Maybe Int`s using `(>>=)` rather than direct `case` analysis

Trong chương 5, bạn đã thấy rằng Idris cung cấp một ký hiệu đặc biệt để sắp xếp các phép toán bằng cách sử dụng (>>=), được giới thiệu bởi từ khóa do. Bạn có thể sử dụng cùng một ký hiệu ở đây và viết maybeAdd như sau.

Listing 6.26.
Adding two `Maybe Int`s using `do` notation rather than using `(>>=)` directly

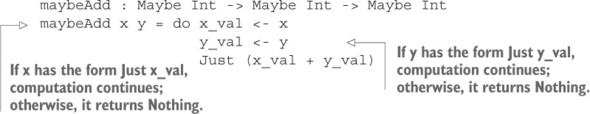
Hình 6.5 cho thấy cách một biểu thức sử dụng cú pháp do được dịch sang một biểu thức sử dụng (>>=). Điều này hoạt động hoàn toàn giống như việc dịch các chương trình IO được viết bằng cú pháp do. Giống như việc dịch cú pháp danh sách thành Nil và (::), việc dịch này chỉ là cú pháp. Do đó, nếu bạn định nghĩa toán tử (>>=) trong một ngữ cảnh khác, Idris sẽ cho phép bạn sử dụng cú pháp do trong ngữ cảnh đó.

Figure 6.5.
Transforming `do` notation to an expression using the `(>>=)` operator

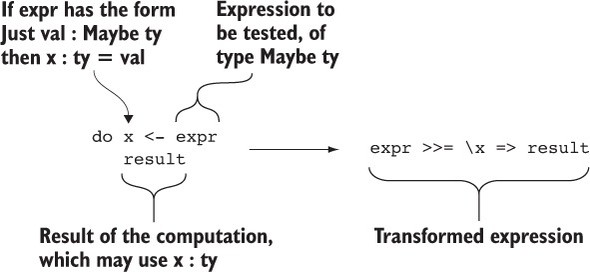
Với cú pháp do, bạn có thể viết trường hợp "schema" cho parseCommand như sau, để cú pháp do, thông qua (>>=), xử lý việc Nothing, cho phép bạn tập trung vào trường hợp thành công của Just schemaok:

parseCommand schema "schema" rest = do schemaok <- parseSchema (words rest) Just (SetSchema schemaok)

Exercises

Update the data store program to support Chars in the schema. You can test your solution at the REPL as follows:

*ex_6_3> :exec Command: schema Char Int OK Command: add x 24 ID 0 Command: add y 17 ID 1 Command: get 0 'x', 24

Modify the get command so that, if given no arguments, it prints the entire contents of the data store. For example:

*ex_6_3> :exec Command: schema Char Int OK Command: add x 24 ID 0 Command: add y 17 ID 1 Command: get 0: 'x', 24 1: 'y', 17

Update the data store program so that it uses do notation rather than nested case blocks, where appropriate.

6.4. Summary

Type synonyms are alternative names for existing types, which allow you to give more-descriptive names to types.
Type-level functions are functions that can be used anywhere that Idris is expecting a Type. Type synonyms are a special case of type-level functions.
Type-level functions can be used to compute types, and they allow you to write functions with varying numbers of arguments, such as printf.
You can represent a schema for a data store as a type, and then use type-level functions to calculate the types of operations, such as parsing and displaying entries in the data store from the schema description.
A record is a data type with only one constructor, and with automatically generated functions for projecting fields from the record.
After refining a data type, you can use holes to correct compilation errors temporarily.
Using do notation, you can sequence computations that use Maybe to capture the possibility of errors.

Chapter 7.
Interfaces: using constrained generic types

Chương này đề cập đến

Constraining generic types using interfaces
Implementing interfaces for specific contexts
Using interfaces defined in the Prelude

Trong chương 2, bạn đã thấy rằng kiểu hàm tổng quát với các biến kiểu có thể bị ràng buộc để các biến đại diện cho một tập hợp các kiểu hạn chế hơn. Ví dụ, bạn đã thấy hàm sau dùng để nhân đôi một số trong bất kỳ kiểu số nào:

double : Num a => a -> a double x = x + x

Loại double bao gồm một ràng buộc, Num a, quy định rằng a chỉ có thể đại diện cho các kiểu số. Do đó, bạn có thể sử dụng double với Int, Nat, Integer, hoặc bất kỳ kiểu số nào khác, nhưng nếu bạn cố gắng sử dụng nó với một kiểu không phải số, chẳng hạn như Bool, Idris sẽ báo lỗi.

Bạn đã thấy một vài ràng buộc như vậy, chẳng hạn như Eq cho các kiểu hỗ trợ kiểm tra tính bình đẳng và Ord cho các kiểu hỗ trợ so sánh. Bạn cũng đã thấy các hàm phụ thuộc vào các ràng buộc khác mà chúng tôi chưa thảo luận chi tiết, chẳng hạn như map và >>=, phụ thuộc vào Functor và Monad tương ứng. Chúng ta vẫn chưa thảo luận về cách các ràng buộc này được định nghĩa hoặc giới thiệu.

Trong chương này, chúng ta sẽ thảo luận về cách định nghĩa và sử dụng các kiểu tổng quát có ràng buộc bằng cách sử dụng giao diện. Trong khai báo kiểu cho double, chẳng hạn, ràng buộc Num a được thực hiện bởi một giao diện, Num, mô tả các phép toán số học sẽ được thực hiện theo nhiều cách khác nhau cho các kiểu số khác nhau.

Type classes in Haskell

Nếu bạn biết Haskell, bạn sẽ quen thuộc với khái niệm lớp kiểu trong Haskell. Giao diện trong Idris tương tự như lớp kiểu trong Haskell và thường được sử dụng theo cách tương tự, tuy nhiên có một số điểm khác biệt. Điều quan trọng nhất là, đầu tiên, giao diện trong Idris có thể được tham số hóa bởi các giá trị của bất kỳ kiểu nào và không bị giới hạn ở các kiểu hoặc bộ tạo kiểu, và thứ hai, giao diện trong Idris có thể có nhiều triển khai, mặc dù chúng tôi sẽ không đi vào chi tiết trong chương này.

Từ góc độ phát triển dựa trên kiểu, interfaces cho phép chúng ta cung cấp mức độ chính xác cần thiết cho các kiểu tổng quát. Nói chung, một interface trong Idris mô tả một tập hợp các thao tác tổng quát có thể được thực hiện theo nhiều cách khác nhau cho các kiểu cụ thể khác nhau. Ví dụ:

You could define an interface for operations that serialize and load generic data to and from JSON.
A graphics library could provide an interface for operations that draw representations of data.

Phần Dẫn Nhập bao gồm một loạt các giao diện, và chúng ta sẽ tập trung vào những giao diện này trong chương này. Chúng ta sẽ bắt đầu bằng cách xem xét chi tiết hai trong số những giao diện quan trọng nhất.

7.1. Generic comparisons with Eq and Ord

Để bắt đầu, chúng ta sẽ xem xét hai giao diện định nghĩa các so sánh tổng quát, cả hai đều được định nghĩa trong Prelude:

Eq, which supports comparing values for equality or inequality.
Ord, which supports comparing values to determine which is larger.

Trong quá trình đó, bạn sẽ học cách khai báo các interface, cách triển khai những interface đó trong các ngữ cảnh cụ thể và cách các interface khác nhau có thể liên quan đến nhau.

7.1.1.
Testing for equality with Eq

Như bạn đã thấy trong chương 2, Idris cung cấp một toán tử để kiểm tra các giá trị có bằng nhau hay không, ==, với một kiểu tổng quát bị ràng buộc:

Idris> :t (==) (==) : Eq ty => ty -> ty -> Bool

Nói cách khác, bạn có thể so sánh hai giá trị của một loại chung nào đó ty để kiểm tra tính bằng nhau, trả về kết quả dưới dạng Bool, với điều kiện rằng ty thỏa mãn ràng buộc Eq. Tương tự, có một toán tử để kiểm tra sự khác biệt:

Idris> :t (/=) (/=) : Eq ty => ty -> ty -> Bool

Specifying multiple constraints

Trong ví dụ trong phần này, tôi đã chỉ định chính xác một ràng buộc, Eq ty. Bạn cũng có thể liệt kê nhiều ràng buộc dưới dạng danh sách ngăn cách bằng dấu phẩy. Ví dụ, kiểu hàm sau đây chỉ ra rằng ty cần phải thỏa mãn cả hai ràng buộc Num và Show:

addAndShow : (Num ty, Show ty) => ty -> ty -> String

Bạn sẽ thấy nhiều ví dụ hơn sau này, trong phần 7.2.2.

Bất kỳ lúc nào bạn sử dụng một trong những toán tử này, bạn phải biết rằng các toán hạng của nó là một kiểu có thể so sánh được về tính bình đẳng. Giả sử, ví dụ, bạn muốn viết một hàm đếm số lần xuất hiện của một giá trị cụ thể, thuộc một kiểu tổng quát nào đó, trong một danh sách. Chúng ta sẽ tạo một hàm gọi là occurrences trong một tệp, Eq.idr:

Type— As always, begin by giving a type for the function and creating a skeleton definition:

occurrences : (item : ty) -> (values : List ty) -> Nat occurrences item xs = ?occurrences_rhs

Define, refine— You can define the function by case splitting on the input list, xs, and refining the hole generated in each case. If it’s an empty list, there can be no occurrences of item, so return 0:
```
occurrences : (item : ty) -> (values : List ty) -> Nat occurrences item [] = 0 occurrences item (value :: values) = ?occurrences_rhs_2
```
Refine— If the input is a non-empty list, try testing the value at the start of the list and item for equality:
```
occurrences : (item : ty) -> (values : List ty) -> Nat occurrences item [] = 0 occurrences item (value :: values) = case value == item of case_val => ?occurrences_rhs_2
```
Unfortunately, Idris reports an error:
```
Eq.idr:3:13: When checking right hand side of occurrences with expected type Nat Can't find implementation for Eq ty
```
This problem is similar to the one we encountered in chapter 3 when defining ins_sort. In this case, value and item have type ty, but there’s no constraint that values of type ty are comparable for equality.

Refine— The solution, as with ins_sort, is to refine the type by adding a constraint:

occurrences : Eq ty => (item : ty) -> (values : List ty) -> Nat

The constraint Eq ty means that you can now use the == operator and complete the definition as follows:

occurrences : Eq ty => (item : ty) -> (values : List ty) -> Nat occurrences item [] = 0 occurrences item (value :: values) = case value == item of False => occurrences item values True => 1 + occurrences item values

Loại cuối cùng của các xảy ra cho biết rằng nó nhận một ty và một List ty làm đầu vào, với điều kiện rằng biến loại ty đại diện cho một loại có thể được so sánh để xác định sự bằng nhau.

Điều này hoạt động tốt cho các kiểu dữ liệu tích hợp sẵn như Char và Integer:

*Eq> occurrences 'b' ['a','a','b','b','b','c'] 3 : Nat *Eq> occurrences 100 [50,100,100,150] 2 : Nat

Nhưng nếu bạn có các kiểu do người dùng định nghĩa thì sao? Giả sử bạn có một kiểu do người dùng định nghĩa tên là Matter, cũng được định nghĩa trong Eq.idr:

data Matter = Solid | Liquid | Gas

Bạn sẽ hy vọng có thể đếm số lần xuất hiện của Liquid trong một danh sách. Thật không may, nếu bạn thử làm điều này, Idris sẽ báo lỗi:

*Eq> occurrences Liquid [Solid, Liquid, Liquid, Gas] Can't find implementation for Eq Matter

Thông báo lỗi này có nghĩa là Idris không biết cách so sánh các giá trị trong kiểu Matter do người dùng định nghĩa để kiểm tra sự bằng nhau. Để sửa chữa điều này, chúng ta cần xem xét cách ràng buộc Eq được định nghĩa và cách giải thích cho Idris biết các kiểu do người dùng định nghĩa như Matter có thể thỏa mãn nó như thế nào.

7.1.2.
Defining the Eq constraint using interfaces and implementations

Các ràng buộc như Eq được định nghĩa trong Idris bằng cách sử dụng giao diện. Một định nghĩa giao diện chứa một tập hợp các hàm liên quan (gọi là phương thức của giao diện) có thể được cung cấp các triển khai khác nhau cho các ngữ cảnh cụ thể. Giao diện Eq được định nghĩa trong Prelude, chứa các phương thức (==) và (/=).

Listing 7.1.
The `Eq` interface (defined in the Prelude)

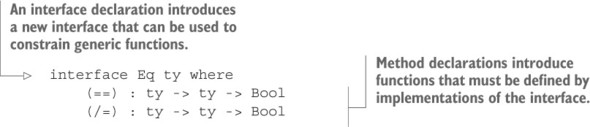
Việc định nghĩa một giao diện giới thiệu các hàm cấp cao mới cho mỗi phương thức của giao diện. Khai báo giao diện trong danh sách 7.1 giới thiệu các hàm cấp cao (==) và (/=). Nếu bạn kiểm tra kiểu của những hàm này, bạn sẽ thấy ràng buộc kiểu Eq ty rõ ràng trong các kiểu của chúng.

(==) : Eq ty => ty -> ty -> Bool (/=) : Eq ty => ty -> ty -> Bool

Hình 7.1 cho thấy các thành phần của khai báo giao diện. Tham số, ty trong trường hợp này, được giả định có kiểu Type theo mặc định và đại diện cho đối số tổng quát cần được ràng buộc. Tham số phải xuất hiện trong mỗi khai báo phương thức.

Figure 7.1.
The `Eq` interface declaration

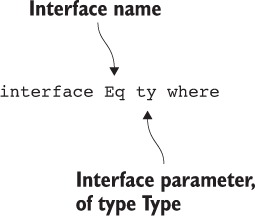
Parameter naming conventions

Các tham số của một giao diện (ty ở đây) thường là các biến kiểu tổng quát, vì vậy tôi thường đặt cho chúng những cái tên ngắn gọn và tổng quát. Tên ty chỉ ra rằng tham số có thể là bất kỳ kiểu nào. Khi có nhiều tham số hơn hoặc khi giao diện có mục đích cụ thể hơn, tôi sẽ đặt những cái tên cụ thể hơn.

Một khai báo giao diện, do đó, cung cấp các kiểu cho các hàm liên quan với một tham số đại diện cho một đối số tổng quát. Để định nghĩa các hàm này cho các trường hợp cụ thể, bạn cần cung cấp các triển khai.

Để viết một triển khai, bạn cung cấp giao diện và một tham số, cùng với định nghĩa cho mỗi phương thức. Danh sách sau đây cho thấy một triển khai cho giao diện Eq, giải thích cách kiểu Matter thoả mãn ràng buộc.

Listing 7.2.
Implementation of `Eq` for `Matter` (Eq.idr)

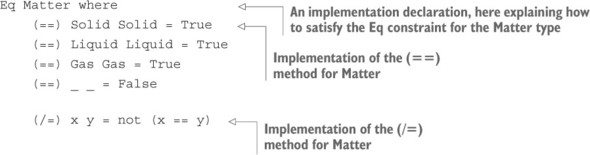
Interactive development of implementations

Như bạn sẽ thấy ngay lập tức, bạn có thể sử dụng Ctrl-Alt-A để cung cấp một triển khai khung cho Eq Matter, giống như với định nghĩa hàm.

Nếu bạn thêm phần triển khai này vào tệp mà bạn đã định nghĩa occurrences và Matter, bạn sẽ có thể sử dụng occurrences với List Matter:

*Eq> occurrences Liquid [Solid, Liquid, Liquid, Gas] 2 : Nat

Điều này cung cấp việc triển khai của hai phương thức, (==) và (/=), mà cần phải được triển khai để có thể so sánh các phần tử của kiểu Matter về sự bằng nhau và không bằng nhau. Lưu ý rằng việc triển khai không chứa bất kỳ khai báo kiểu nào, vì các khai báo này đã được cung cấp trong khai báo giao diện.

Interface documentation

Nếu bạn sử dụng :doc trên một giao diện tại REPL, hoặc Ctrl-Alt-D trên tên giao diện trong Atom, Idris sẽ hiển thị tài liệu cho giao diện đó bao gồm các tham số, phương thức và danh sách các cài đặt đã biết. Ví dụ, đây là những gì nó trông như thế cho Eq:

Idris> :doc Eq Interface Eq The Eq interface defines inequality and equality. Parameters: ty Methods: (==) : Eq ty => ty -> ty -> Bool infixl 5 The function is Total (/=) : Eq ty => ty -> ty -> Bool infixl 5 The function is Total Implementations: Eq () Eq Int Eq Integer Eq Double [...]

Bạn có thể xây dựng triển khai một cách tương tác trong Atom như sau:

Type— Start by giving the implementation header on its own:
```
Eq Matter where
```
This a Type step because it instantiates the types of (==) and (/=), with Matter standing for the parameter a.
Define— You can also use the interactive editing tools in Atom to build implementations of interfaces. With the cursor over Eq, press Ctrl-Alt-A, and Idris will add skeleton definitions for (==) and (/=) with generic names for the arguments:
```
Eq Matter where (==) x y = ?Eq_rhs_1 (/=) x y = ?Eq_rhs_2
```
Type— If you check the type of ?Eq_rhs_1, you’ll see confirmation that x and y are of type Matter:
```
 x : Matter y : Matter -------------------------------------- Eq_rhs_1 : Bool
```

Define— You can begin by defining (==) by case splitting on x:

Eq Matter where (==) Solid y = ?Eq_rhs_3 (==) Liquid y = ?Eq_rhs_4 (==) Gas y = ?Eq_rhs_5 (/=) x y = ?Eq_rhs_2

Refine— Each value of type Matter is only equal to itself, so you can refine the definition as follows, with a catchall case to handle when the inputs aren’t equal:
```
Eq Matter where (==) Solid Solid = True (==) Liquid Liquid = True (==) Gas Gas = True (==) _ _ = False (/=) x y = ?Eq_rhs_2
```
Remember that the order of cases is important, and Idris will try to match the clauses in order, so the catchall case must be at the end.
Refine— To complete the implementation, you need to define (/=). The simplest definition is to use (==) and then invert the result:
```
Eq Matter where (==) Solid Solid = True (==) Liquid Liquid = True (==) Gas Gas = True (==) _ _ = False (/=) x y = not (x == y)
```

Khi bạn khai báo một giao diện, bạn giới thiệu một tập hợp các hàm tổng quát liên quan mới, được gọi là phương thức, mà có thể được nạp chồng cho các tình huống cụ thể. Khi bạn định nghĩa một cài đặt cho giao diện, bạn phải cung cấp định nghĩa cho tất cả các phương thức của nó. Vì vậy, khi bạn định nghĩa thể hiện Eq cho Matter, bạn phải cung cấp định nghĩa cho cả (==) và (/=).

7.1.3.
Default method definitions

Giao diện định nghĩa một tập hợp các phương thức liên quan, chẳng hạn như (==) và (/=). Trong một số trường hợp, các phương thức có mối quan hệ chặt chẽ đến nỗi bạn có thể định nghĩa chúng dựa trên các phương thức khác trong giao diện. Ví dụ, bạn luôn mong đợi kết quả của x /= y sẽ là ngược lại với kết quả của x == y, bất kể giá trị hoặc thậm chí kiểu của x và y là gì.

Trong tình huống này, Idris cho phép bạn cung cấp một định nghĩa mặc định cho một phương thức. Nếu một cài đặt không cung cấp định nghĩa cho một phương thức có định nghĩa mặc định, Idris sẽ sử dụng định nghĩa mặc định đó. Ví dụ, giao diện Eq cung cấp các định nghĩa mặc định cho cả (==) và (/=), mỗi cái được định nghĩa dựa trên cái kia, như sau.

Listing 7.3.
`Eq` interface with default method definitions

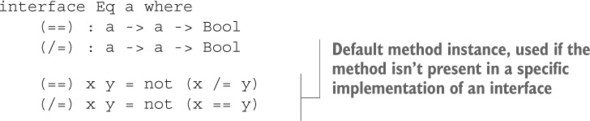
Bạn có thể cung cấp một triển khai của Eq cho Matter bằng cách chỉ định một định nghĩa cho (==), và sử dụng triển khai phương thức mặc định cho (/=):

Eq Matter where (==) Solid Solid = True (==) Liquid Liquid = True (==) Gas Gas = True (==) _ _ = False

Các định nghĩa phương thức mặc định có nghĩa là khi bạn định nghĩa một triển khai của Eq, bạn có thể cung cấp định nghĩa cho một hoặc cả hai phép so sánh (==) và (/=).

7.1.4.
Constrained implementations

Khi viết các triển khai cho các loại chung, bạn có thể phát hiện ra nhu cầu về các ràng buộc bổ sung đối với các tham số của các loại chung. Ví dụ, để kiểm tra xem hai danh sách có bằng nhau hay không, bạn sẽ cần biết cách so sánh các loại phần tử để xác định sự bằng nhau.

Trong chương 4, bạn đã thấy loại tổng quát của cây nhị phân, được định nghĩa như sau trong tree.idr:

data Tree elem = Empty | Node (Tree elem) elem (Tree elem)

Để kiểm tra xem hai cây có bằng nhau hay không, bạn cũng cần có khả năng so sánh các kiểu phần tử. Hãy xem điều gì xảy ra nếu bạn cố gắng định nghĩa một triển khai của Eq cho các cây với một kiểu phần tử tổng quát:

Type— Begin by writing the implementation header, stating the interface you wish to implement and the type for which you’re implementing it:
```
Eq (Tree elem) where
```
Define— Add a skeleton definition that gives template definitions for all the methods of the interface:
```
Eq (Tree elem) where (==) x y = ?Eq_rhs_1 (/=) x y = ?Eq_rhs_2
```
You can use the default definition for (/=), so you can delete the second method:
```
Eq (Tree elem) where (==) x y = ?Eq_rhs_1
```
Define— As with the Eq implementation for Matter, you can define (==) by case splitting on each argument and using a catchall case for cases where the inputs are unequal. You know that Empty equals itself, Nodes are equal if all their arguments are equal, and everything else is not equal:
```
Eq (Tree elem) where (==) Empty Empty = True (==) (Node left e right) (Node left' e' right') = ?Eq_rhs_3 (==) _ _ = False
```
For the moment, you’ve left a hole, ?Eq_rhs_3, for the details of comparing Nodes.
Refine— You’d expect to be able to complete the definition by refining the ?Eq_rhs_3 hole to say that you can compare each corresponding argument:
```
Eq (Tree elem) where (==) Empty Empty = True (==) (Node left e right) (Node left' e' right') = left == left' && e == e' && right == right' (==) _ _ = False
```
But, unfortunately, Idris reports a problem:
```
Can't find implementation for Eq elem
```
You can compare left and left' for equality, and correspondingly right and right', because they’re of type Tree elem, and the implementation can be recursive; you’re currently defining equality for Tree elem. But e and e' are of type elem, a generic type, and you don’t necessarily know how to compare elem for equality.

Refine—

The solution is to refine the implementation declaration by constraining it to require that elem also has an implementation of Eq available:

Eq elem => Eq (Tree elem) where (==) Empty Empty = True (==) (Node left e right) (Node left' e' right') = left == left' && e == e' && right == right' (==) _ _ = False

Ràng buộc xuất hiện bên trái mũi tên, =>, giống như cách các ràng buộc xuất hiện trong các khai báo kiểu. Hình 7.2 cho thấy các thành phần của tiêu đề giao diện này.

Figure 7.2.
Constrained implementation header

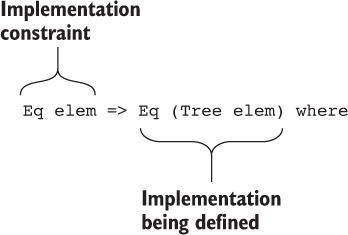
Bạn có thể đọc tiêu đề này như nói rằng cây tổng quát có thể được so sánh để xác định sự bình đẳng, với điều kiện rằng kiểu phần tử của chúng cũng có thể được so sánh để xác định sự bình đẳng. Bạn có thể giới thiệu các ràng buộc giao diện như vậy bất kỳ nơi nào bạn giới thiệu một biến kiểu, nếu bạn cần ràng buộc biến kiểu đó thêm nữa.

Limitations on implementation parameters

Bạn đã thấy các cài đặt của Eq được tham số hóa bởi Matter và Tree elem, cả hai đều thuộc loại Type. Nhưng bạn không thể tham số hóa các cài đặt bằng mọi thứ thuộc loại Type. Bạn bị giới hạn bởi các tên được giới thiệu bởi một khai báo data hoặc record, hoặc các kiểu nguyên thủy. Cụ thể, điều này có nghĩa là bạn không thể tham số hóa các cài đặt bằng các từ đồng nghĩa kiểu hoặc các hàm tính toán kiểu.

Bạn đã thấy các hạn chế về khai báo kiểu, và ở đây bạn đã thấy một hạn chế trong định nghĩa thực thi. Tương tự, bạn có thể đặt các hạn chế cho chính các định nghĩa giao diện.

7.1.5.
Constrained interfaces: defining orderings with Ord

Nếu bạn đặt một ràng buộc trên định nghĩa giao diện, bạn đang mở rộng một giao diện hiện có. Trong Prelude, ví dụ, có một giao diện Ord, được hiển thị trong danh sách tiếp theo, mở rộng Eq để hỗ trợ việc sắp xếp các giá trị.

Listing 7.4.
The `Ord` Interface, which extends `Eq` (defined in the Prelude)

Tất cả các phương thức, ngoại trừ phương thức so sánh, đều có định nghĩa mặc định, một số trong số đó được viết dựa trên phương thức so sánh, và một số khác sử dụng phương thức (==) được cung cấp bởi giao diện Eq.

Nếu bạn có một triển khai của Ord cho một kiểu dữ liệu nào đó, bạn có thể sắp xếp các danh sách chứa kiểu đó:

sort : Ord ty => List ty -> List ty

Chẳng hạn, bạn có thể có một kiểu dữ liệu đại diện cho bộ sưu tập nhạc, với các bản ghi chứa tiêu đề, nghệ sĩ và năm phát hành, và bạn có thể muốn sắp xếp chúng trước theo tên nghệ sĩ, sau đó theo năm phát hành, và cuối cùng theo tiêu đề. Danh sách sau đây cung cấp một định nghĩa về kiểu dữ liệu này kèm theo một số ví dụ.

Listing 7.5.
A record data type and a collection to be sorted (Ord.idr)

Nếu bạn cố gắng sắp xếp bộ sưu tập như hiện tại, Idris sẽ báo cáo rằng nó không biết cách sắp xếp các giá trị của loại Album:

*Ord> sort collection Can't find implementation for Ord Album

Danh sách 7.6 cho thấy cách bạn có thể giải thích cho Idris cách đặt hàng Album. Đầu tiên, bạn cần cung cấp một triển khai Eq, vì ràng buộc trên giao diện Ord yêu cầu rằng các triển khai của Ord cũng phải là các triển khai của Eq. Triển khai Eq kiểm tra xem từng trường có giá trị giống nhau hay không; triển khai Ord so sánh theo tên nghệ sĩ, sau đó theo năm, và sau đó theo tiêu đề nếu hai trường đầu tiên bằng nhau.

Listing 7.6.
Implementations of `Eq` and `Ord` for `Album`

Việc triển khai Ord cho Album có nghĩa là bạn có thể sử dụng các toán tử so sánh thông thường trên các giá trị kiểu Album:

*Ord> heroes > clouds False : Bool *Ord> help <= rubbersoul True : Bool

Nó cũng có nghĩa là bạn có thể sử dụng bất kỳ hàm nào với ràng buộc Ord, chẳng hạn như sắp xếp. Ví dụ, bạn có thể sắp xếp tập hợp và liệt kê các tiêu đề theo thứ tự đã sắp xếp:

*Ord> map title (sort collection) ["Hunky Dory", "Heroes", "Clouds", "Help", "Rubber Soul"] : List String

Đưa ra các ràng buộc về giao diện, như ràng buộc Eq trên Ord, cho phép bạn định nghĩa các hệ thống phân cấp của các giao diện. Vì vậy, ví dụ, nếu có một triển khai của Ord cho một số kiểu dữ liệu, bạn có thể an tâm rằng cũng có một triển khai của Eq cho kiểu dữ liệu đó. Prelude định nghĩa một số giao diện, một số được sắp xếp thành các phân cấp, và chúng ta sẽ xem xét một số cái quan trọng nhất trong phần tiếp theo.

Exercises

Đối với những bài tập này, bạn sẽ sử dụng kiểu Shape được định nghĩa trong chương 4:

data Shape = Triangle Double Double | Rectangle Double Double | Circle Double

Implement Eq for Shape. You can test your answer at the REPL as follows:

*ex_7_1> Circle 4 == Circle 4 True : Bool *ex_7_1> Circle 4 == Circle 5 False : Bool *ex_7_1> Circle 4 == Triangle 3 2 False : Bool

Implement Ord for Shape. Shapes should be ordered by area, so that shapes with a larger area are considered greater than shapes with a smaller area. You can test this by trying to sort the following list of Shapes:
```
testShapes : List Shape testShapes = [Circle 3, Triangle 3 9, Rectangle 2 6, Circle 4, Rectangle 2 7]
```
You should see the following when sorting the list at the REPL:
```
*ex_7_1> sort testShapes [Rectangle 2.0 6.0, Triangle 3.0 9.0, Rectangle 2.0 7.0, Circle 3.0, Circle 4.0] : List Shape
```

7.2. Interfaces defined in the Prelude

Prelude Idris cung cấp một số giao diện thường được sử dụng, ngoài Eq và Ord, như bạn vừa thấy. Trong phần này và phần tiếp theo, tôi sẽ mô tả ngắn gọn một vài giao diện quan trọng nhất. Chúng ta đã gặp một số trong số đó: Show, Num, Cast, Functor và Monad. Ở đây, bạn sẽ thấy cách định nghĩa các giao diện này, nơi chúng có thể được sử dụng, và một số ví dụ về cách bạn có thể viết các triển khai cho các kiểu của riêng bạn.

Các tham số của một giao diện (nói cách khác, các biến được đưa ra trong tiêu đề giao diện) có thể có bất kỳ kiểu nào. Nếu không có kiểu rõ ràng được chỉ định trong tiêu đề giao diện cho một tham số, thì nó được mặc định là kiểu Type. Trong phần này, chúng ta sẽ xem xét một số giao diện được tham số hóa bởi các kiểu.

7.2.1.
Converting to String with Show

Trong chương 2, bạn đã thấy hàm show, cái chuyển đổi một giá trị thành một chuỗi. Đây là một phương thức của giao diện Show, được định nghĩa trong Prelude và được hiển thị trong danh sách sau. Cả hai phương thức show và showPrec đều có các triển khai mặc định, mỗi cái đều được định nghĩa dựa trên cái khác. Ở đây, chúng ta chỉ xem xét show.

Listing 7.7.
The `Show` interface (defined in the Prelude)

Precedence contexts

Mục đích của showPrec là có thể hiển thị các biểu thức phức tạp trong dấu ngoặc nếu cần thiết. Điều này có thể hữu ích nếu, ví dụ, bạn có một đại diện cho các công thức số học, nơi các quy tắc về độ ưu tiên yêu cầu một số biểu thức con cần phải được đặt trong dấu ngoặc. Mặc định, showPrec gọi show trực tiếp, và đối với hầu hết các mục đích hiển thị, điều này hoàn toàn đủ. Nếu bạn muốn tìm hiểu thêm, hãy xem tài liệu bằng cách sử dụng :doc.

Prelude cung cấp hai hàm sử dụng show để chuyển đổi một giá trị thành một chuỗi và sau đó xuất nó ra console, có hoặc không có ký tự xuống dòng cuối cùng:

printLn : Show ty => ty -> IO () print : Show ty => ty -> IO ()

Bạn có thể định nghĩa một triển khai Show đơn giản cho kiểu Album:

Show Album where show (MkAlbum artist title year) = title ++ " by " ++ artist ++ " (released " ++ show year ++ ")"

Sau đó, bạn có thể in một Album ra console bằng cách sử dụng printLn. Ví dụ:

*Ord> :exec printLn hunkydory Hunky Dory by David Bowie (released 1971)

Giao diện Show chủ yếu được sử dụng để xuất thông tin gỡ lỗi, hiển thị giá trị của các kiểu dữ liệu phức tạp dưới dạng dễ đọc cho con người.

7.2.2.
Defining numeric types

Prelude cung cấp một hệ thống phân cấp các giao diện với các phương thức cho các phép toán số. Những giao diện này chia các toán tử thành nhiều nhóm:

The Num interface—Contains operations that work on all numeric types, including addition, multiplication, and conversion from integer literals
The Neg interface—Contains operations that work on numeric types that can be negative, including negation, subtraction, and absolute value
The Integral interface—Contains operations that work on integer types
The Fractional interface—Contains operations that work on numeric types that can be divided into fractions

Danh sách sau đây cho thấy cách các giao diện này được định nghĩa.

Listing 7.8.
The numeric interface hierarchy (defined in the Prelude)

Thật hữu ích khi biết các phép toán nào có sẵn trên các kiểu dữ liệu nào. Bảng 7.1 tóm tắt các giao diện số và các triển khai tồn tại cho mỗi loại trong Prelude.

Table 7.1.
Summary of numeric interfaces and their implementations

Giao diện	Mô tả	Triển khai
Num	All numeric types	Integer, Int, Nat, Double
Neg	Numeric types that can be negative	Integer, Int, Double
Integral	Integer types	Integer, Int, Nat
Fractional	Numeric types that can be divided into fractions	Double

Một phương pháp đặc biệt đáng lưu ý là từInteger. Tất cả các hằng số nguyên trong Idris được chuyển đổi ngầm định sang kiểu số phù hợp bằng cách sử dụng từInteger. Do đó, miễn là có một triển khai của Num cho một kiểu số, bạn có thể sử dụng các hằng số nguyên cho kiểu đó.

Bằng cách tạo ra các triển khai mới của Num và các giao diện liên quan, bạn có thể sử dụng ký hiệu số học tiêu chuẩn và các hằng số số nguyên cho các kiểu của riêng bạn. Ví dụ, danh sách 7.9 cho thấy một kiểu dữ liệu Expr đại diện cho các biểu thức số học, bao gồm một phép toán "giá trị tuyệt đối" và một hàm eval tính toán kết quả của việc đánh giá một biểu thức.

Listing 7.9.
An arithmetic expression data type and an evaluator (Expr.idr)

Để xây dựng một biểu thức, bạn cần áp dụng các bộ tạo của Expr trực tiếp. Ví dụ, để biểu diễn biểu thức 6 + 3 * 12, và để tính toán nó, bạn sẽ cần viết như sau:

*Expr> Add (Val 6) (Mul (Val 3) (Val 12)) Add (Val 6) (Mul (Val 3) (Val 12)) : Expr Integer *Expr> eval (Add (Val 6) (Mul (Val 3) (Val 12))) 42 : Integer

Nếu ngược lại, bạn tạo một triển khai Num cho Expr, bạn sẽ có thể sử dụng ký hiệu số học chuẩn (với +, *, và các hằng số nguyên) để xây dựng các giá trị của kiểu Expr. Nếu hơn nữa, bạn tạo một triển khai Neg, bạn sẽ có thể sử dụng các số âm và phép trừ. Danh sách sau đây cho thấy cách bạn có thể làm điều này.

Listing 7.10.
Implementations of `Num` and `Neg` for `Expr` (Expr.idr)

Function composition

Hàm (.) cung cấp cho bạn một ký hiệu ngắn gọn để kết hợp hai hàm. Nó có kiểu và định nghĩa như sau:

(.) : (b -> c) -> (a -> b) -> a -> c (.) func_bc func_ab x = func_bc (func_ab x)

Trong ví dụ ở danh sách 7.10, bạn có thể đã viết như sau:

fromInteger x = Val (fromInteger x)

Hàm (.) cho phép bạn viết như sau:

fromInteger x = (Val . fromInteger) x

Cuối cùng, thay vì có x như một đối số ở cả hai bên, bạn có thể sử dụng khái niệm ứng dụng từng phần:

fromInteger = Val . fromInteger

Để xây dựng một biểu thức và đánh giá nó, bạn có thể sử dụng ký hiệu chuẩn:

*Expr> the (Expr _) (6 + 3 * 12) Add (Val 6) (Mul (Val 3) (Val 12)) : Expr Integer *Expr> eval (6 + 3 * 12) 42 : Integer

Trong trường hợp đầu tiên, bạn cần sử dụng để làm rõ rằng biểu thức số nên được diễn giải là một Expr, thay vì mặc định, điều này sẽ là một Integer. Trong trường hợp thứ hai, Idris suy ra từ kiểu của eval rằng đối số phải là một Expr.

7.2.3.
Converting between types with Cast

Trong chương 2, bạn đã thấy hàm cast, được sử dụng để chuyển đổi giá trị giữa các loại tương thích khác nhau. Nếu bạn xem loại của cast, bạn sẽ thấy rằng nó có một loại generic bị ràng buộc mà sử dụng một interface Cast:

Idris> :t cast cast : Cast from to => from -> to

Khác với các giao diện mà chúng ta đã thấy cho đến nay, Cast có hai tham số thay vì một. Danh sách tiếp theo cung cấp định nghĩa của nó. Giao diện trong Idris có thể có bất kỳ số lượng tham số nào (thậm chí là không có tham số!).

Listing 7.11.
The `Cast` interface (defined in the Prelude)

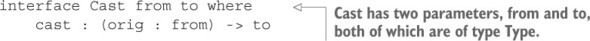
Như chúng ta đã quan sát ở chương 2, việc chuyển đổi bằng cách sử dụng cast có thể bị mất dữ liệu. Idris định nghĩa các phép chuyển đổi giữa Double và Integer, chẳng hạn, điều này có thể làm mất độ chính xác. Mục đích của cast là cung cấp một hàm tổng quát tiện lợi, với một tên dễ nhớ, cho các phép chuyển đổi.

Để định nghĩa một triển khai của một giao diện với nhiều tham số, bạn cần cung cấp cả hai tham số cụ thể. Ví dụ, bạn có thể định nghĩa một phép chuyển đổi từ Maybe elem sang List elem, vì bạn có thể coi Maybe elem như một danh sách có chứa không hoặc một phần tử elems.

Cast (Maybe elem) (List elem) where cast Nothing = [] cast (Just x) = [x]

Bạn cũng có thể định nghĩa việc chuyển đổi theo hướng ngược lại, từ danh sách phần tử sang Maybe phần tử, nhưng điều này có thể làm mất thông tin, vì bạn sẽ cần phải quyết định phần tử nào để lấy nếu danh sách có nhiều hơn một phần tử.

Exercises

Implement Show for the Expr type defined in section 7.2.2. Hint: To keep this simple and avoid concerns about precedence, assume all subexpressions can be written in parentheses. You can test your answer at the REPL as follows:
```
*ex_7_2> show (the (Expr _) (6 + 3 * 12)) "(6 + (3 * 12))" : String *ex_7_2> show (the (Expr _) (6 * 3 + 12)) "((6 * 3) + 12)" : String
```
Implement Eq for the Expr type. Expressions should be considered equal if their evaluation is equal. So, for example, you should see the following:
```
*Expr> the (Expr _) (2 + 4) == 3 + 3 True : Bool *Expr> the (Expr _) (2 + 4) == 3 + 4 False : Bool
```
Hint: Start with the implementation header Eq (Expr ty) where, and add constraints as you discover you need them.
Implement Cast to allow conversions from Expr num to any appropriately constrained type num. Hint: You’ll need to evaluate the expression, which should tell you how num needs to be constrained. You can test your answer at the REPL as follows:
```
*ex_7_2> let x : Expr Integer = 6 * 3 + 12 in the Integer (cast x) 30 : Integer
```

7.3. Interfaces parameterized by Type -> Type

Trong tất cả các giao diện mà chúng ta đã thấy cho đến nay, các tham số đều là Loại. Tuy nhiên, không có bất kỳ hạn chế nào về các loại tham số có thể là gì. Đặc biệt, việc các giao diện có tham số theo kiểu Loại -> Loại là rất phổ biến. Ví dụ, bạn đã thấy các hàm sau với các loại bị ràng buộc:

map : Functor f => (a -> b) -> f a -> f b pure : Applicative f => a -> f a (>>=) : Monad m => m a -> (a -> m b) -> m b

Trong mỗi trường hợp, tham số f hoặc m đại diện cho một kiểu tham số, chẳng hạn như List hoặc IO. Bạn đã thấy map trong bối cảnh của List, và pure và (>>=) trong bối cảnh của IO.

Trong phần này, chúng ta sẽ xem xét cách mà các phép toán này và các phép toán khác được định nghĩa chung trong Prelude bằng cách sử dụng các giao diện, cùng với một số ví dụ về cách áp dụng chúng cho các kiểu dữ liệu của riêng bạn.

7.3.1.
Applying a function across a structure with Functor

Trong chương 2, bạn đã thấy hàm map, nó áp dụng một hàm cho mỗi phần tử trong một danh sách:

Idris> map (*2) [1,2,3,4] [2, 4, 6, 8] : List Integer

Tuy nhiên, tôi nhận thấy rằng bản đồ không chỉ giới hạn ở các danh sách, mà thực tế còn có một kiểu tổng quát bị ràng buộc bằng giao diện Functor. Functor cho phép bạn áp dụng một hàm một cách đồng nhất trên một kiểu tổng quát. Ví dụ trước đó đã áp dụng hàm "nhân với hai" một cách đồng nhất trên một danh sách các số nguyên.

Danh sách dưới đây cho thấy định nghĩa của giao diện Functor, chứa phương thức map là phương thức duy nhất của nó, và sự triển khai của nó cho List, như được định nghĩa trong Prelude.

Listing 7.12.
The `Functor` interface and an implementation for `List` (defined in the Prelude)

Cho đến nay, các giao diện mà chúng ta đã thấy đều được tham số hóa bởi một biến có kiểu Type. Nhưng tham số của Functor lại là một kiểu đã được tham số hóa (chẳng hạn như List). Khi tham số có bất kỳ kiểu nào khác ngoài Type, bạn cần chỉ định rõ ràng kiểu của tham số đó.

Thường thì rất hữu ích khi cung cấp một triển khai của Functor cho các cấu trúc dữ liệu tập hợp. Ví dụ, danh sách sau đây cho thấy cách định nghĩa một triển khai Functor cho cây nhị phân, áp dụng đồng bộ một hàm cho mọi phần tử xuất hiện tại một Node.

Listing 7.13.
Implementation of `Functor` for `Tree` (Tree.idr)

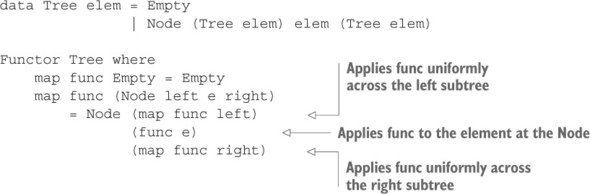
`Prelude cung cấp các cài đặt Functor cho tất cả các kiểu với một tham số kiểu duy nhất, khi có thể, bao gồm List, Maybe và IO. Nếu bạn nhập Data.Vect, cũng có một cài đặt Functor cho Vect n, như sau.`

Listing 7.14.
Implementation of `Functor` for vectors (defined in Data.Vect)

Tham số trong tiêu đề của triển khai, Vect n, có nghĩa là bạn đang định nghĩa một triển khai của Functor cho các vector có bất kỳ độ dài nào. Các quy tắc thông thường cho các tham số ngầm định áp dụng, như đã mô tả trong chương 3: bất kỳ tên nào bắt đầu bằng chữ cái thường trong vị trí tham số của hàm đều được coi là một tham số ngầm định. Do đó, n được coi là một tham số ngầm định ở đây.

7.3.2.
Reducing a structure using Foldable

Nếu bạn ghi lại một danh sách các số theo dạng 1 :: 2 :: 3 :: 4 :: [], bạn có thể tính tổng các số bằng cách áp dụng các quy tắc sau:

Replace each :: with a + (giving 1 + 2 + 3 + 4 + []).
Replace the [] with a 0 (giving 1 + 2 + 3 + 4 + 0).
Calculate the value of the resulting expression (giving 10).

Hoặc bạn có thể tính sản phẩm của các số bằng cách áp dụng các quy tắc sau:

Replace each :: with a * (giving 1 * 2 * 3 * 4 * []).
Replace the [] with a 1 (giving 1 * 2 * 3 * 4 * 1).
Calculate the value of the resulting expression (giving 24).

Nói chung, chúng tôi đang giảm nội dung của danh sách xuống một giá trị duy nhất bằng cách thay thế [] bằng một giá trị mặc định hoặc khởi tạo, và thay thế :: bằng một hàm nhận hai đối số, kết hợp mỗi giá trị với kết quả của việc giảm phần còn lại của danh sách. Idris cung cấp hai hàm bậc cao, được gọi là folds, để gợi ý việc gập cấu trúc thành một giá trị duy nhất, để thực hiện chính xác điều này:

foldr : (elem -> acc -> acc) -> acc -> List elem -> acc foldl : (acc -> elem -> acc) -> acc -> List elem -> acc

Sự khác biệt giữa foldr và foldl nằm ở cách diễn đạt kết quả. Trong ví dụ đầu tiên của chúng ta, foldr sẽ tính kết quả là 1 + (2 + (3 + (4 + 0))), trong khi foldl sẽ tính kết quả là (((0 + 1) + 2) + 3) + 4. Nói cách khác, foldr xử lý các phần tử từ trái sang phải, và foldl xử lý các phần tử từ phải sang trái.

Type variables in foldl and foldr

Tên của các biến trong các loại foldl và foldr gợi ý về mục đích của chúng: elem là kiểu phần tử của danh sách và acc là kiểu của kết quả. Tên acc gợi ý về kiểu của một tham số tích lũy, trong đó kết quả cuối cùng được tính toán.

Trong mỗi trường hợp, đối số đầu tiên là hàm (hoặc toán tử) cần áp dụng, và đối số thứ hai là giá trị khởi đầu. Vì vậy, bạn có thể tính toán hai ví dụ trước đó như sau:

Idris> foldr (+) 0 [1,2,3,4] 10 : Integer Idris> foldr (*) 1 [1,2,3,4] 24 : Integer

Hoặc bạn có thể sử dụng hàm gập để tính tổng độ dài của các chuỗi trong danh sách chuỗi. Ví dụ, tổng độ dài của ["Một", "Hai", "Ba"] nên là 11.

Hãy viết điều này một cách tương tác, sử dụng foldr, trong một tệp có tên là Fold.idr:

Type, define—You can begin with a type and a candidate definition, and apply foldr to the input list, xs, but leave holes for the function and initial value so their types can give you hints as to how to proceed:
```
totalLen : List String -> Nat totalLen xs = foldr ?sumLength ?initial xs
```

Type, refine—The type of ?initial tells you that the initial value must be a Nat:

 xs : List String t : Type -> Type elem : Type -------------------------------------- initial : Nat

You can initialize it with 0, because the total length of an empty list of strings is 0:

totalLen : List String -> Nat totalLen xs = foldr ?sumLength 0 xs

Type, refine—The type and context of ?sumLength tells you that you need to provide a function:
```
 xs : List String t : Type -> Type elem : Type -------------------------------------- sumLength : String -> Nat -> Nat
```
The function you need to provide takes a String (standing for the string at a given position in the list) and a Nat (standing for the result of folding the rest of the list), and returns a Nat (standing for the total length). You can complete the definition as follows:
```
totalLen : List String -> Nat totalLen xs = foldr (\str, len => length str + len) 0 xs
```

Bạn có thể kiểm tra hàm kết quả tại REPL:

*Fold> totalLen ["One", "Two", "Three"] 11 : Nat

Trong ví dụ trước, tôi đã đưa ra một kiểu cho foldr cụ thể cho List. Nhưng nếu bạn nhìn vào kiểu tại REPL, bạn sẽ thấy một kiểu tổng quát bị ràng buộc sử dụng giao diện Foldable.

foldr : Foldable t => (elem -> acc -> acc) -> acc -> t elem -> acc

Một cài đặt của Foldable cho một cấu trúc giải thích cách giảm cấu trúc đó thành một giá trị duy nhất bằng cách sử dụng một giá trị khởi đầu và một hàm để kết hợp mỗi phần tử với một cấu trúc đã gập tổng thể. Danh sách sau đây cung cấp định nghĩa giao diện. Có một định nghĩa mặc định cho foldl, được viết dựa trên foldr, vì vậy chỉ cần triển khai foldr.

Listing 7.15.
The `Foldable` interface (defined in the Prelude)

Danh sách tiếp theo cho thấy cách Foldable được triển khai trong Prelude cho List. Lưu ý đặc biệt sự khác biệt giữa các triển khai của foldr và foldl.

Listing 7.16.
Implementation of `Foldable` for `List` (defined in the Prelude)

Bởi vì kiểu dữ liệu Cây của chúng ta là một kiểu tổng quát chứa một tập hợp các giá trị, bạn nên có thể cung cấp một triển khai Foldable:

Type— Begin by providing an implementation header and a skeleton definition of foldr. You can use the default definition for foldl:
```
Foldable Tree where foldr func acc tree = ?Foldable_rhs_1
```

Define, refine—Case-split on the tree. If the tree is Empty, you return the initial value:

Foldable Tree where foldr func acc Empty = acc foldr func acc (Node left e right) = ?Foldable_rhs_3

Refine— In the Node case, because foldr works left to right, you begin by folding the left subtree recursively. Figure 7.3 illustrates this with an example, assuming an initial accumulator of 0.
Figure 7.3.
Fold the left subtree with the initial accumulator. This gives you 0 + 1 + 2 + 3 = 6.

In code, it looks like this: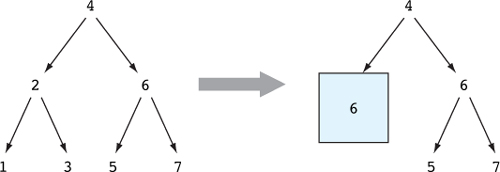
```
Foldable Tree where foldr func acc Empty = acc foldr func acc (Node left e right) = let leftfold = foldr func acc left in ?Foldable_rhs_3
```
Refine— Next, take the result of folding the left subtree (leftfold) and use it as the initial value when folding the right subtree. Figure 7.4 illustrates this on the same example.
Figure 7.4.
Fold the right subtree, initialized with the result of folding the left subtree. This gives you 6 + 5 + 6 + 7 = 24.

In code, it looks like this: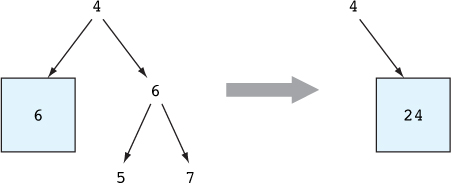
```
Foldable Tree where foldr func acc Empty = acc foldr func acc (Node left e right) = let leftfold = foldr func acc left rightfold = foldr func leftfold right in ?Foldable_rhs_3
```

Refine— Finally, apply func to the value at the node e and the result of folding the right subtree:

Foldable Tree where foldr func acc Empty = acc foldr func acc (Node left e right) = let leftfold = foldr func acc left rightfold = foldr func leftfold right in func e rightfold

In the example, this gives you the result 4 + 24 = 28.

7.3.3.
Generic do notation using Monad and Applicative

Có hai giao diện khác mà bạn nên biết đến, và bạn đã thấy chúng trong thực tế: Monad và Applicative. Trong hầu hết các trường hợp, bạn khó có khả năng cần cung cấp các triển khai riêng của mình, nhưng chúng xuất hiện trong toàn bộ thư viện Prelude và base, vì vậy sẽ hữu ích khi biết khả năng của chúng, đặc biệt là các hàm mà chúng cung cấp.

Trong chương 5, bạn đã thấy cách hàm (>>=) được sử dụng để sắp xếp các hoạt động IO:

(>>=) : IO a -> (a -> IO b) -> IO b

Sau đó, trong chương 6, bạn đã thấy cách mà hàm (>>=) được sử dụng để tuần tự hóa các phép toán Maybe, bỏ qua chuỗi nếu bất kỳ phép toán nào trả về Nothing:

(>>=) : Maybe a -> (a -> Maybe b) -> Maybe b

Vì hai hàm này có kiểu tương tự (thay thế trực tiếp IO bằng Maybe) và mục đích tương tự (thực hiện các hành động tương tác hoặc các phép tính có thể thất bại), bạn có thể mong đợi chúng được định nghĩa trong một giao diện chung. Danh sách sau đây hiển thị giao diện Monad cung cấp (>>=), cùng với một phương thức join kết hợp các cấu trúc monadic lồng nhau.

Sure, please provide the text you would like me to translate into Vietnamese.
We won’t go into detail on join here, but it allows you to define a Monad implementation for List by concatenating lists of lists, among other things.

Listing 7.17.
The `Monad` interface (defined in the Prelude)

Cả hai (>>=) và join đều có định nghĩa mặc định, vì vậy bạn có thể định nghĩa một triển khai Monad dựa trên bất kỳ cái nào. Ở đây, chúng ta sẽ tập trung vào (>>=).

Trong chương 6, bạn đã thấy một định nghĩa của (>>=) cho Maybe. Trong thực tế, nó được định nghĩa trong Prelude như sau:

Monad Maybe where (>>=) Nothing next = Nothing (>>=) (Just x) next = next x

Bạn cũng đã thấy hàm thuần túy, đặc biệt trong bối cảnh các chương trình IO để tạo ra một giá trị trong một tính toán IO mà không mô tả bất kỳ hành động nào:

pure : a -> IO a

Cũng như (>>=), pure cũng hoạt động trong ngữ cảnh của Maybe, áp dụng Just cho đối số của nó:

Idris> the (Maybe _) (pure "driven snow") Just "driven snow" : Maybe String

Một lần nữa, vì pure hoạt động trong nhiều ngữ cảnh, bạn có thể mong đợi nó được định nghĩa trong một giao diện. Danh sách sau đây cho thấy định nghĩa của giao diện Applicative, cung cấp pure và một hàm (<*>) áp dụng một hàm bên trong một cấu trúc. Bạn sẽ thấy một ví dụ về Applicative trong chương 12.

Listing 7.18.
The `Applicative` interface (defined in the Prelude)

interface Functor f => Applicative (f : Type -> Type) where pure : a -> f a (<*>) : f (a -> b) -> f a -> f b

Có một số ứng dụng thực tiễn của Monad và Applicative, mặc dù với tư cách là người dùng một thư viện, bạn thường chỉ cần biết liệu có các thể hiện Monad và Applicative cho các kiểu đã cho hay không, và đặc biệt là ảnh hưởng của toán tử (>>=) là gì.

Một triển khai thú vị của Monad trong Prelude là cho List. Hàm (>>=) cho List truyền mỗi giá trị trong danh sách đầu vào tới hàm tiếp theo trong chuỗi, và kết hợp các kết quả thành một danh sách mới. Tôi sẽ không đi vào chi tiết về điều này trong cuốn sách này, nhưng bạn có thể sử dụng nó để viết các chương trình phi xác định.

Còn rất nhiều điều cần nói về chủ đề giao diện, đặc biệt là hệ thống phân cấp mà chúng ta đã xem xét một cách ngắn gọn trong phần này, bao gồm Functor, Foldable, Applicative và Monad. Một cuộc thảo luận sâu về nó nằm ngoài phạm vi của cuốn sách này, nhưng các giao diện mà chúng ta đã thảo luận trong chương này là những giao diện bạn sẽ gặp thường xuyên nhất trong giai đoạn đầu.

Exercises

Implement Functor for Expr (defined in section 7.2.2). You can test your answer at the REPL as follows:

*Expr> map (*2) (the (Expr _) (1 + 2 * 3)) Add (Val 2) (Mul (Val 4) (Val 6)) : Expr Integer *Expr> map show (the (Expr _) (1 + 2 * 3)) Add (Val "1") (Mul (Val "2") (Val "3")) : Expr String

Implement Eq and Foldable for Vect. Hint: If you import Data.Vect, these implementations already exist, so you’ll need to define Vect by hand to try this exercise. You can test your answers at the REPL as follows:
```
*ex_7_3> foldr (+) 0 (the (Vect _ _) [1,2,3,4,5]) 15 : Integer *ex_7_3> the (Vect _ _) [1,2,3,4] == [1,2,3,4] True : Bool *ex_7_3> the (Vect _ _) [1,2,3,4] == [5,6,7,8] False : Bool
```

7.4. Summary

Generic types can be constrained using interfaces, which describe groups of functions that can be applied in a specific context.
The Eq interface provides functions for comparing values for equality and inequality.
The Ord interface provides functions for comparing two values to see which is smaller or larger.
Implementations of interfaces describe how interfaces can be evaluated in specific contexts.
Interfaces and implementations can themselves have constraints. Constraints say which interfaces must be implemented for a definition to be valid.
The Prelude provides several standard interfaces, including Show for converting values to a String, Num for arithmetic operations and numeric literals, and Cast for converting between types.
Interfaces can be parameterized by values of any type. Several in the Prelude are parameterized by values of type Type -> Type.
An implementation of Functor for a structure allows a uniform action to be applied to each element in the structure.
An implementation of Foldable allows a structure to be reduced to a single value.
An implementation of Monad allows you to use do notation to sequence computations on a structure.

Chapter 8.
Equality: expressing relationships between data

Chương này đề cập đến

Expressing properties of functions and data
Checking and guaranteeing equalities between data
Showing when cases are impossible with the empty type Void

Bạn đã thấy một số cách mà các kiểu hạng nhất tăng cường khả năng biểu đạt của hệ thống kiểu, và độ chính xác của các kiểu mà chúng ta gán cho các hàm. Bạn đã thấy cách sử dụng độ chính xác tăng cường trong các kiểu (kèm theo các lỗ hổng) để giúp viết các hàm, và cách viết các hàm để tính toán các kiểu. Một cách khác bạn có thể sử dụng các kiểu hạng nhất để tăng cường độ chính xác của các kiểu của bạn, và tăng cường sự tự tin vào việc các hàm hoạt động đúng, là viết các kiểu cụ thể để biểu đạt các thuộc tính của dữ liệu và các mối quan hệ giữa dữ liệu.

Trong chương này, chúng ta sẽ xem xét một thuộc tính đơn giản, sử dụng kiểu để biểu đạt các đảm bảo rằng các giá trị là bằng nhau. Bạn cũng sẽ thấy cách biểu đạt các đảm bảo rằng các giá trị không bằng nhau. Các thuộc tính như sự bình đẳng và bất bình đẳng đôi khi là cần thiết khi bạn đang định nghĩa các hàm phức tạp hơn với các kiểu phụ thuộc, nơi mối quan hệ giữa các giá trị có thể không ngay lập tức rõ ràng đối với Idris. Ví dụ, như bạn sẽ thấy khi chúng ta định nghĩa hàm đảo ngược trên các vectơ, độ dài của vectơ đầu vào và đầu ra phải giống nhau, vì vậy chúng ta sẽ cần phải giải thích cho trình biên dịch tại sao độ dài được bảo tồn.

Chúng ta sẽ bắt đầu bằng cách xem xét một hàm mà chúng ta đã sử dụng, exactLength, và xem xét một cách chi tiết cách xây dựng nó từ những nguyên tắc cơ bản.

8.1. Guaranteeing equivalence of data with equality types

Khi bạn muốn so sánh các giá trị để kiểm tra tính bằng nhau, bạn có thể sử dụng toán tử ==, toán tử này trả về một giá trị có kiểu Bool, với hai giá trị trong một kiểu ty mà đã có cài đặt giao diện Eq.

(==) : Eq ty => ty -> ty -> Bool

Nhưng nếu bạn nhìn kỹ vào kiểu này, nó cho bạn biết điều gì về mối quan hệ giữa các đầu vào (kiểu ty) và đầu ra (kiểu Bool)?

Trên thực tế, nó không cho bạn biết gì cả! Nếu không xem xét cụ thể cách cài đặt, bạn không biết chính xác cách == sẽ hoạt động. Bất kỳ hành vi nào sau đây đều là hành vi hợp lý cho một cài đặt của == trong giao diện Eq, ít nhất là về mặt kiểu dữ liệu:

Always returning True
Always returning False
Returning whether the inputs are not equal

Sẽ rất bất ngờ đối với các lập trình viên nếu toán tử == hoạt động theo bất kỳ cách nào trong số này, nhưng về phía bộ kiểm tra kiểu của Idris, nó không thể đưa ra bất kỳ giả định nào ngoài những gì được đưa ra một cách rõ ràng trong kiểu. Do đó, nếu bạn muốn so sánh các giá trị ở mức kiểu, bạn sẽ cần một cái gì đó biểu đạt hơn.

Trên thực tế, bạn đã thấy một ví dụ về tình huống mà bạn có thể muốn làm điều này: vào cuối chương 5, bạn đã sử dụng hàm exactLength để kiểm tra xem một Vect có độ dài cụ thể hay không:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a)

Bạn đã sử dụng chức năng này để kiểm tra xem hai vector do người dùng nhập vào có cùng chiều dài hay không. Với một chiều dài cụ thể, len, và một vector có chiều dài, m, nó trả về các kết quả sau:

Nothing, if len is not the same as m
Just input, if len is the same as m

Trong phần này, chúng ta sẽ xem xét cách triển khai exactLength bằng cách biểu diễn sự đồng nhất dưới dạng kiểu, và bạn sẽ thấy rõ hơn tại sao == không đủ. Chúng ta sẽ bắt đầu bằng cách cố gắng triển khai nó bằng == và xem chúng ta gặp phải những hạn chế ở đâu.

8.1.1.
Implementing exactLength, first attempt

Thay vì nhập Data.Vect, nơi định nghĩa exactLength, chúng ta sẽ bắt đầu bằng cách định nghĩa Vect thủ công và cung cấp một kiểu dữ liệu cùng với khung định nghĩa của exactLength. Danh sách sau đây cho thấy điểm khởi đầu của chúng ta, trong một tập tin có tên ExactLength.idr.

Listing 8.1.
A definition of `Vect` and the type and skeleton definition of `exactLength` (ExactLength.idr)

data Vect : Nat -> Type -> Type where Nil : Vect Z a (::) : a -> Vect k a -> Vect (S k) a exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength len input = ?exactLength_rhs

Bạn nên mong đợi có thể thực hiện exactLength bằng cách so sánh độ dài của đầu vào với độ dài mong muốn, len. Nếu chúng bằng nhau, thì đầu vào có độ dài len, vì vậy kiểu của nó nên được coi là tương đương với Vect len a, và bạn có thể trả về nó trực tiếp. Ngược lại, bạn sẽ trả về Nothing.

Là một nỗ lực đầu tiên, bạn có thể thử các bước sau:

Define— Because m doesn’t appear on the left side of the skeleton definition, you’ll need to bring it into scope explicitly in order to compare len and m. You can do this by updating the definition to the following:
```
exactLength {m} len input = ?exactLength_rhs
```
Recall from chapter 3 that an implicit argument such as m can be used in the definition if it’s written inside braces on the left side.

Define— You can now compare m and len for equality using == and inspect the result in a case statement:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case m == len of False => ?exactLength_rhs_1 True => ?exactLength_rhs_2

Refine— For ?exactLength_rhs_1, the lengths are different, so you return Nothing:

exactLength {m} len input = case m == len of False => Nothing True => ?exactLength_rhs_2

Refine— For ?exactLength_rhs_2, you’d like to return Just input because the lengths are equal. You can start with Just:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case m == len of False => Nothing True => Just ?exactLength_rhs_2

Type—
Then, you can take a look at the types of the variables in scope, and the type required to fill in the ?exactLength_rhs_2 hole:
```
 a : Type m : Nat len : Nat input : Vect m a -------------------------------------- exactLength_rhs_2 : Vect len a
```
Even though you’ve checked that m and len are equal using ==, you can’t fill in the hole with input because it has type Vect m a, and the required type is Vect len a. The problem, as when defining zipInputs at the end of chapter 5, is that the type of == isn’t informative enough to guarantee that m and len are equal, even if it returns True. You will, therefore, need to consider alternative approaches to implementing exactLength, using a more informative type when comparing m and len.

Loại của một biến cho Idris biết những giá trị nào có thể mà biến đó có, nhưng nó không nói gì về nguồn gốc của giá trị. Nếu một biến có loại Bool, Idris biết rằng nó có thể có một trong hai giá trị True hoặc False, nhưng không có thông tin gì về phép toán đã tạo ra giá trị đó. Có rất nhiều phép toán có thể sản xuất ra một kết quả có loại Bool ngoài việc kiểm tra sự bằng nhau. Hơn nữa, sự bằng nhau được định nghĩa bởi giao diện Eq, và không có đảm bảo nào trong loại về cách mà giao diện đó có thể được triển khai.

Thay vào đó, bạn cần tạo ra một kiểu chính xác hơn cho phép kiểm tra sự bằng nhau, trong đó kiểu này đảm bảo rằng một phép so sánh giữa hai đầu vào chỉ có thể thành công nếu các đầu vào thực sự giống hệt nhau. Trong phần còn lại của mục này, bạn sẽ thấy cách thực hiện điều này từ những nguyên tắc cơ bản, và cách sử dụng kiểu bằng nhau mới để thực hiện exactLength.

8.1.2.
Expressing equality of Nats as a type

Danh sách 8.2 hiển thị một kiểu phụ thuộc, EqNat. Nó có hai số làm đối số, num1 và num2. Nếu bạn có một giá trị có kiểu EqNat num1 num2, bạn biết rằng num1 và num2 phải là cùng một số vì bộ khởi tạo duy nhất, Same, chỉ có thể xây dựng một thứ với kiểu theo dạng EqNat num num, trong đó hai đối số là giống nhau.

Listing 8.2.
Representing equal `Nat`s as a type (EqNat.idr)

Với các loại phụ thuộc, bạn có thể sử dụng các loại như EqNat để biểu thị thông tin bổ sung về dữ liệu khác, trong trường hợp này là biểu thị rằng hai số tự nhiên (Nat) được đảm bảo là bằng nhau. Đây là một khái niệm mạnh mẽ, như bạn sẽ sớm thấy, và có thể mất một thời gian để hoàn toàn đánh giá được. Do đó, chúng ta sẽ xem xét việc biểu diễn và kiểm tra các sự tương đương một cách sâu sắc.

Đầu tiên, để xem cách EqNat hoạt động, hãy thử một vài ví dụ tại REPL:

*EqNat> Same 4 Same 4 : EqNat 4 4 *EqNat> Same 5 Same 5 : EqNat 5 5 *EqNat> the (EqNat 3 3) (Same _) Same 3 : EqNat 3 3 *EqNat> Same (2 + 2) Same 4 : EqNat 4 4

Dù bạn cố gắng thế nào, tham số trong kiểu vẫn được lặp lại. Tuy nhiên, việc viết một kiểu với các tham số không bằng nhau hoàn toàn hợp lệ.

*EqNat> EqNat 3 4 EqNat 3 4 : Type

Nhưng nếu bạn cố gắng xây dựng một giá trị với kiểu này, bạn sẽ không thành công và luôn gặp lỗi kiểu.

*EqNat> the (EqNat 3 4) (Same _) (input):1:5:When checking argument value to function Prelude.Basics.the: Type mismatch between EqNat num num (Type of Same num) and EqNat 3 4 (Expected type) Specifically: Type mismatch between 0 and 1

Thông báo lỗi này chỉ ra rằng 3 và 4 cần phải giống nhau, vì cả hai đều cần được khởi tạo cho num trong kiểu Same. Kiểu EqNat 3 4 là một kiểu trống, có nghĩa là không có giá trị nào của kiểu đó.

Specificity in error messages

Bạn sẽ nhận thấy rằng trong các thông báo lỗi, Idris thường báo cáo lỗi theo hai cách. Phần đầu tiên đưa ra sự không phù hợp về kiểu tổng thể. Tuy nhiên, điều này có thể trở nên khá lớn, vì vậy Idris cũng báo cáo phần cụ thể của biểu thức không khớp. Ở đây, nó báo cáo sự không phù hợp giữa 0 và 1 do cách mà Nat được định nghĩa dựa trên Z và S. Sự không phù hợp tổng thể giữa S (S (S Z)) và S (S (S (S Z))), trong đó sự khác biệt cụ thể là giữa Z và S Z.

8.1.3.
Testing for equality of Nats

Chúng tôi sẽ sử dụng EqNat để giúp triển khai exactLength. Vì EqNat num1 num2 về cơ bản là một chứng minh rằng num1 phải bằng num2, chúng tôi sẽ viết một hàm kiểm tra xem các độ dài đầu vào có bằng nhau hay không, và nếu có, biểu thị sự bình đẳng đó như một trường hợp của EqNat.

Chúng ta sẽ bắt đầu bằng cách viết một hàm checkEqNat, hàm này sẽ trả về một chứng minh rằng các đầu vào của nó giống nhau, dưới dạng EqNat, hoặc Nothing nếu các đầu vào khác nhau. Nó có kiểu sau đây:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2)

Một khi được triển khai, nó sẽ hoạt động như trong các ví dụ sau:

*EqNat> checkEqNat 5 5 Just (Same 5) : Maybe (EqNat 5 5) *EqNat> checkEqNat 1 2 Nothing : Maybe (EqNat 1 2)

Vì chúng ta chỉ có thể có một giá trị của loại EqNat num1 num2 cho một num1 và num2 cụ thể nếu num1 và num2 giống hệt nhau, loại của checkEqNat đảm bảo rằng nếu nó thành công (tức là, trả về một giá trị có dạng Just p), thì các đầu vào của nó thực sự phải bằng nhau.

Bạn có thể thực hiện hàm như sau:

Type— Begin with a type and a skeleton definition:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2) checkEqNat num1 num2 = ?checkEqNat_rhs

Define— You can define the function by case splitting on both Nat inputs. First, case-split on num1:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2) checkEqNat Z num2 = ?checkEqNat_rhs_1 checkEqNat (S k) num2 = ?checkEqNat_rhs_2

Define— Then, case-split on num2 in both cases:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2) checkEqNat Z Z = ?checkEqNat_rhs_3 checkEqNat Z (S k) = ?checkEqNat_rhs_4 checkEqNat (S k) Z = ?checkEqNat_rhs_1 checkEqNat (S k) (S j) = ?checkEqNat_rhs_5

Refine— If you take a look at the type of the ?checkEqNat_rhs_3 hole, you’ll see that you need to provide evidence that 0 is the same as itself, so you can fill this in with Just (Same 0). For ?checkEqNat_rhs_4 and ?checkEqNat_rhs_1, you can’t provide any evidence that 0 is the same as a non-zero number, so return Nothing. You now have this:
```
checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2) checkEqNat Z Z = Just (Same 0) checkEqNat Z (S k) = Nothing checkEqNat (S k) Z = Nothing checkEqNat (S k) (S j) = ?checkEqNat_rhs_5
```
Refine— The result for ?checkEqNat_rhs_5 depends on whether k is equal to j, which you can determine by making a recursive call and then case splitting on the result:
```
checkEqNat (S k) (S j) = case checkEqNat k j of case_val => ?checkEqNat_rhs_5
```
Define—
Case splitting on case_val leads to cases for when k and j aren’t equal (Nothing) and when they are equal (Just x). You can rename the Just x produced by the case split to something more informative, and fill in the case where the recursive call produces Nothing:
```
checkEqNat (S k) (S j) = case checkEqNat k j of Nothing => Nothing Just eq => ?checkEqNat_rhs_2
```
Type— Looking at the type of checkEqNat_rhs_2 gives you some information about how to proceed:
```
 k : Nat j : Nat eq : EqNat k j -------------------------------------- checkEqNat_rhs_2 : Maybe (EqNat (S k) (S j))
```
The type of eq is EqNat k j, and you’re looking for something of type Maybe (EqNat (S k) (S j)).
Refine— If k and j are equal, you know that S k and S j must be equal, so you can return a value constructed with Just:
```
checkEqNat (S k) (S j) = case checkEqNat k j of Nothing => Nothing Just eq => Just ?checkEqNat_rhs_2
```

Refine— To complete the definition, rename the remaining hole, and lift it to a top-level definition, which you’ll implement in the next section.

sameS : (eq : EqNat k j) -> EqNat (S k) (S j) checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (EqNat num1 num2) checkEqNat Z Z = Just (Same Z) checkEqNat Z (S k) = Nothing checkEqNat (S k) Z = Nothing checkEqNat (S k) (S j) = case checkEqNat k j of Nothing => Nothing Just eq => Just (sameS eq)

Bạn có thể thấy từ loại của định nghĩa lifted, sameS, rằng đây là một hàm nhận bằng chứng rằng k và j là bằng nhau, và trả về bằng chứng rằng S k và S j là bằng nhau. Bằng cách thể hiện sự bình đẳng giữa các số dạng như một kiểu dữ liệu tùy thuộc, EqNat, bạn có thể viết các hàm như sameS mà nhận một thể hiện của EqNat làm đầu vào và thao tác với chúng, về cơ bản suy diễn thêm thông tin về sự bình đẳng.

8.1.4.
Functions as proofs: manipulating equalities

Không thể tạo ra một thể hiện của EqNat k j khi k và j khác nhau, điều này có nghĩa là bạn có thể coi sameS như một bằng chứng rằng nếu k và j bằng nhau, thì S k và S j cũng bằng nhau.

Bây giờ hãy thử triển khai sameS. Để rõ ràng hơn, chúng ta sẽ làm cho các tham số Nat trở nên rõ ràng:

sameS : (k : Nat) -> (j : Nat) -> (eq : EqNat k j) -> EqNat (S k) (S j) sameS k j eq = ?sameS_rhs

Bạn có thể thực hiện sameS với các bước sau:

Define— Begin by creating a skeleton definition:

sameS : (k : Nat) -> (j : Nat) -> (eq : EqNat k j) -> EqNat (S k) (S j) sameS k j eq = ?sameS_rhs

Define— Next, in Atom, ask to case-split on eq:
```
sameS : (k : Nat) -> (j : Nat) -> (eq : EqNat k j) -> EqNat (S k) (S j) sameS k k (Same k) = ?sameS_rhs_1
```
Notice that k appears three times on the left side of this definition! Because you’ve expressed a relationship between k and j using eq in the type of sameS, and you’ve case-split on eq, Idris has noticed that both Nat inputs must be the same. Not only that, if you try to give a different value, it will report an error. If, instead, you write this,
```
sameS k j (Same k) = ?sameS_rhs_1
```
then Idris will report the following:
```
EqNat.idr:15:7:When checking left hand side of sameS: Type mismatch between j (Inferred value) and k (Given value)
```
In other words, because the type states that both Nat inputs must be the same, Idris isn’t happy that they’re different. So, revert to the left side that Idris generated after the case split on eq:
```
sameS : (k : Nat) -> (j : Nat) -> (eq : EqNat k j) -> EqNat (S k) (S j) sameS k k (Same k) = ?sameS_rhs_1
```
Type— If you check the type of ?sameS_rhs_1, you’ll see that you need to provide evidence that S k is the same as itself:
```
 k : Nat -------------------------------------- sameS_rhs_1 : EqNat (S k) (S k)
```

Refine— You can therefore complete the definition as follows:

sameS : (k : Nat) -> (j : Nat) -> (eq : EqNat k j) -> EqNat (S k) (S j) sameS k k (Same k) = Same (S k)

Proofs in Idris

Về nguyên tắc, bạn có thể phát biểu và thử chứng minh các thuộc tính phức tạp của bất kỳ hàm nào trong Idris. Ví dụ, bạn có thể viết một hàm mà kiểu của nó phát biểu rằng việc đảo ngược một danh sách hai lần sẽ cho ra danh sách ban đầu. Tuy nhiên, trên thực tế, bạn sẽ hiếm khi cần thao tác với các đẳng thức phức tạp hơn nhiều so với việc triển khai sameS. Tuy nhiên, bạn sẽ thấy một chút về việc thao tác với các đẳng thức và nơi chúng xuất hiện khi định nghĩa các hàm trong phần 8.2.

Danh sách 8.3 đưa ra định nghĩa đầy đủ của checkEqNat, sử dụng phiên bản của sameS với các tham số rõ ràng. Bạn cũng có thể viết hàm này mà không cần sử dụng sameS, mà thay vào đó sử dụng phân tích trường hợp trên eq. Bạn cũng có thể sử dụng cú pháp do, như đã mô tả ở cuối chương 6, để làm cho định nghĩa ngắn gọn hơn. Như các bài tập, hãy thử cài đặt lại nó theo từng cách này.

Listing 8.3.
Testing for equality of `Nat`s with `EqNat` (EqNat.idr)

Khác với ==, checkEqNat biểu thị mối quan hệ giữa đầu vào và đầu ra của nó một cách chính xác trong kiểu của nó. Sử dụng điều này, chúng ta có thể thực hiện một nỗ lực khác để triển khai exact-Length.

8.1.5.
Implementing exactLength, second attempt

Trước đó, chúng tôi đã đạt được điểm sau trong việc triển khai exactLength, trước khi xác định rằng một so sánh Boolean là không đủ:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case m == len of False => ?exactLength_rhs_1 True => ?exactLength_rhs_2

Thay vì sử dụng toán tử so sánh Boolean == để so sánh m và len, bạn có thể thử sử dụng checkEqNat m len. Điều này sẽ trả về một giá trị có kiểu Maybe (EqNat m len), vì vậy nếu m và len bằng nhau, bạn sẽ có một số thông tin bổ sung trong kiểu dữ liệu cho biết chính xác ý nghĩa của kết quả so sánh. Trong nỗ lực thứ hai này, bạn có thể triển khai hàm như sau:

Define— As before, begin with a type and a skeleton definition, bringing m into scope on the left side:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = ?exactLength_rhs

Define— Instead of defining the function by case splitting on the result of m == len, case-split on the result of checkEqNat:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case checkEqNat m len of Nothing => ?exactLength_rhs_1 Just eq_nat => ?exactLength_rhs_2

Refine— If checkEqNat returns Nothing, the inputs were different, so the input vector is the wrong length:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case checkEqNat m len of Nothing => Nothing Just eq_nat => Just ?exactLength_rhs_2

Type— If checkEqNat returns Just eq_nat, the lengths are equal, and eq_nat provides evidence that they’re equal. For ?exactLength_rhs_2, you have this:
```
 m : Nat len : Nat eq_nat : EqNat m len a : Type input : Vect m a -------------------------------------- exactLength_rhs_2 : Maybe (Vect len a)
```
Define— As before, you still need to provide a result of type Maybe (Vect len a), and all you have available is input of type Vect m a. But you also have eq_nat, which provides evidence that m and len are equal. If you case-split on eq_nat, you’ll get the following:
```
exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case checkEqNat m len of Nothing => Nothing Just (Same len) => ?exactLength_rhs_1
```
Then, when inspecting the type of the new hole, ?exactLength_rhs_1, you’ll see this:
```
 m : Nat a : Type input : Vect len a -------------------------------------- exactLength_rhs_1 : Maybe (Vect len a)
```
Because eq_nat can only take the form Same len, and the type of Same len forces m to be identical to len, Idris has refined the required type to be Maybe (Vect len a).

Refine— From here, it’s easy to complete the definition:

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case checkEqNat m len of Nothing => Nothing Just (Same len) => Just input

Định nghĩa này không hoàn toàn giống với định nghĩa được sử dụng trong Prelude. Thay vào đó, Prelude sử dụng một loại equality tổng quát, được tích hợp trong Idris.

8.1.6.
Equality in general: the = type

Thay vì định nghĩa một loại và hàm so sánh cụ thể cho mỗi loại có thể cần so sánh, chẳng hạn như Nat với EqNat và checkEqNat ở đây, Idris cung cấp một loại so sánh chung. Điều này được tích hợp vào cú pháp của Idris, nên bạn không thể tự định nghĩa điều này (bởi vì = là một ký hiệu được bảo reserved), nhưng về mặt khái niệm, nó sẽ được định nghĩa như sau.

Listing 8.4.
Conceptual definition of a generic equality type

Tên Refl là viết tắt của reflexive, một thuật ngữ toán học có nghĩa là một giá trị bằng chính nó. Giống như EqNat, bạn có thể thử một số ví dụ tại REPL:

Idris> the ("Hello" = "Hello") Refl Refl : "Hello" = "Hello" Idris> the (True = True) Refl Refl : True = True

Nếu bạn đưa ra các biểu thức phức tạp hơn như một phần của kiểu, Idris sẽ đánh giá chúng. Ví dụ, nếu bạn đưa biểu thức 2 + 2 như một phần của kiểu, 2 + 2 = 4, Idris sẽ đánh giá nó:

Idris> the (2 + 2 = 4) Refl Refl : 4 = 4

Như trước đây, nếu bạn cố gắng sử dụng Refl để xây dựng một thể loại bình đẳng bằng cách sử dụng hai giá trị khác nhau, bạn sẽ nhận được một lỗi:

Idris> the (True = False) Refl (input):1:5:When checking argument value to function Prelude.Basics.the: Type mismatch between x = x (Type of Refl) and True = False (Expected type) Specifically: Type mismatch between True and False

Sử dụng kiểu sự bằng built-in, thay vì EqNat, bạn có thể định nghĩa checkEqNat như sau.

Listing 8.5.
Checking equality between `Nat`s using the generic equality type (CheckEqMaybe.idr)

Congruence

Trong danh sách 8.5, bạn đã sử dụng cong để chuyển đổi một giá trị có kiểu k = j thành một giá trị có kiểu S k = S j. Nó có kiểu sau:

cong : {func : a -> b} -> x = y -> func x = func y

Nói cách khác, với một số hàm (ngầm) func, nếu bạn có hai giá trị bằng nhau, thì việc áp dụng func cho các giá trị đó sẽ cho ra kết quả bằng nhau. Điều này thực hiện công việc tương tự như sameS, sử dụng kiểu so sánh chung.

Exercises

Implement the following function, which states that if you add the same value onto the front of equal lists, the resulting lists are also equal:
```
same_cons : {xs : List a} -> {ys : List a} -> xs = ys -> x :: xs = x :: ys
```
Because this function represents an equality proof, it’s sufficient to know that your definition type-checks and is total:
```
*ex_8_1> :total same_cons Main.same_cons is Total
```
Implement the following function, which states that if two values, x and y, are equal, and two lists, xs and ys, are equal, then the two lists x :: xs and y :: ys must also be equal:
```
same_lists : {xs : List a} -> {ys : List a} -> x = y -> xs = ys -> x :: xs = y :: ys
```
Again, it’s sufficient to know that your definition type-checks.
Define a type, ThreeEq, that expresses that three values must be equal. Hint: ThreeEq should have the type a -> b -> c -> Type.
Implement the following function, which uses ThreeEq:
```
allSameS : (x, y, z : Nat) -> ThreeEq x y z -> ThreeEq (S x) (S y) (S z)
```
What does this type mean?

8.2. Equality in practice: types and reasoning

Các chứng minh bình đẳng, và các hàm thao tác chúng, có thể hữu ích khi định nghĩa các hàm với kiểu phụ thuộc. Bạn đã thấy một ví dụ nhỏ về điều này khi triển khai checkEqNat, nơi bạn đã viết một hàm sameS để chỉ ra rằng việc cộng một vào các số bằng nhau dẫn đến các số bằng nhau.

Lý luận về bình đẳng thường trở nên cần thiết khi viết các hàm trên các kiểu được chỉ mục bởi các số. Ví dụ, khi thao tác với các vectơ, bạn có thể cần chứng minh sự tương đương giữa hai biểu thức với các số tự nhiên xuất hiện trong các kiểu của vectơ. Để thấy điều này có thể xảy ra như thế nào và làm thế nào để giải quyết nó, chúng ta sẽ xem xét cách implement một hàm đảo ngược một Vect.

8.2.1.
Reversing a vector

Nếu bạn import Data.Vect, bạn sẽ có quyền truy cập vào một hàm đảo ngược một vector, với kiểu sau:

reverse : Vect n elem -> Vect n elem

Loại này cho biết rằng việc đảo ngược một vector sẽ bảo toàn độ dài của vector đầu vào. Bạn sẽ mong đợi rằng việc triển khai chức năng này sẽ khá đơn giản bằng cách sử dụng các quy tắc sau:

If the input vector is empty, return an empty vector.
If the input vector isn’t empty and has a head x and a tail xs, reverse xs and append x.

Hãy xem điều gì sẽ xảy ra nếu chúng ta cố gắng triển khai phiên bản của riêng mình, myReverse, trong tệp ReverseVec.idr:

Type, define— Begin with a type and a skeleton definition, and case-split on the input:

myReverse : Vect n elem -> Vect n elem myReverse [] = ?myReverse_rhs_1 myReverse (x :: xs) = ?myReverse_rhs_2

Refine— For ?myReverse_rhs_1, return an empty vector:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = ?myReverse_rhs_2

Refine failure—For ?myReverse_rhs_2, you’d like to be able to reverse xs and append x, as follows, but unfortunately this fails:
The error message tells you that Idris has found a mismatch between the type of the value you’ve given, Vect (k + 1), and the expected type, Vect (S k):
```
ReverseVec.idr:6:12: When checking right hand side of myReverse with expected type Vect (S k) elem Type mismatch between Vect (k + 1) elem (Type of myReverse xs ++ [x]) and Vect (S k) elem (Expected type)
```
This seems surprising, because our knowledge of the behavior of addition suggests that S k and k + 1 will always evaluate to the same result, whatever the value of k.

Chúng ta sẽ hoãn việc hoàn thành định nghĩa này và xem xét kỹ lưỡng cách kiểm tra kiểu trong Idris để hiểu những gì đã sai và cách chúng ta có thể sửa chữa điều đó.

8.2.2.
Type checking and evaluation

Khi Idris kiểm tra kiểu của một biểu thức, nó sẽ xem xét kiểu mong đợi của biểu thức đó và kiểm tra rằng kiểu của biểu thức đã cho khớp với nó, sau khi đánh giá cả hai. Đoạn mã sau đây sẽ được kiểm tra kiểu:

test1 : Vect 4 Int test1 = [1, 2, 3, 4] test2: Vect (2 + 2) Int test2 = test1

Mặc dù test1 và test2 có các biểu thức khác nhau trong kiểu của chúng, nhưng những biểu thức này cho kết quả giống nhau, vì vậy bạn có thể định nghĩa test2 để trả về test1.

Bạn có thể thấy tại REPL cách loại kiểm tra Idris đánh giá các loại chứa biến loại bằng cách sử dụng một hàm ẩn danh (được giải thích trong chương 2) để giới thiệu các biến có giá trị chưa biết. Hãy xem xét ví dụ này:

*ReverseVec> \k, elem => Vect (1 + k) elem \k => \elem => Vect (S k) elem : Nat -> Type -> Type

Ở đây, Idris đã đánh giá 1 + k trong kiểu S k. Nhưng nếu bạn thử hoán đổi các đối số của +, bạn sẽ nhận được một kết quả khác:

*ReverseVec> \k, elem => Vect (k + 1) elem \k => \elem => Vect (plus k 1) elem : Nat -> Type -> Type

Ở đây, Idris đã đánh giá k + 1 thành plus k 1, trong đó plus là hàm Prelude thực hiện phép cộng trên Nat. Để hiểu lý do cho sự khác biệt, bạn cần xem định nghĩa của plus. Bạn có thể làm điều này bằng cách sử dụng lệnh REPL :printdef, lệnh này sẽ in ra định nghĩa theo kiểu phân tích mẫu của hàm được truyền vào làm đối số.

*ReverseVec> :printdef plus plus : Nat -> Nat -> Nat plus 0 right = right plus (S left) right = S (plus left right)

Bởi vì hàm cộng được định nghĩa bằng cách so khớp mẫu trên tham số đầu tiên, Idris không thể đánh giá plus k 1 thêm nữa. Để làm điều đó, nó cần biết dạng của k, nhưng hiện tại, không có điều khoản nào cho hàm cộng phù hợp.

Quay trở lại vấn đề của chúng ta với việc định nghĩa myReverse, hãy xem xét trạng thái hiện tại:

Nếu bạn viết lại định nghĩa bằng cách sử dụng let để xây dựng từng thành phần của kết quả, và để một khoảng trống cho giá trị trả về, bạn có thể thấy rõ hơn vấn đề mà bạn cần giải quyết:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = let rev_xs = myReverse xs result = rev_xs ++ [x] in ?myReverse_rhs_2

Kiểm tra kiểu của ?myReverse_rhs_2 cho thấy kiểu của từng thành phần và kiểu yêu cầu của kết quả:

 elem : Type x : elem k : Nat xs : Vect k elem rev_xs : Vect k elem result : Vect (plus k 1) elem -------------------------------------- myReverse_rhs_2 : Vect (S k) elem

Để có kết quả mong muốn, bạn có một biểu thức với loại Vect (k + 1) elem, nhưng bạn cần một biểu thức với loại Vect (S k) elem.

Bạn biết, từ việc thử nghiệm đánh giá tại REPL trước đó, rằng Vect (1 + k) elem sẽ đánh giá đến kiểu mà bạn cần, vì vậy bạn cần phải giải thích cho Idris rằng 1 + k bằng k + 1; hoặc, khi được đánh giá, rằng S k bằng plus k 1. Thư viện Idris cung cấp một hàm có thể giúp bạn:

plusCommutative : (left : Nat) -> (right : Nat) -> left + right = right + left

"Nếu bạn kiểm tra kiểu của plusCommutative tại REPL với các giá trị 1 và k cho bên trái và bên phải, bạn sẽ thấy chính xác sự bình đẳng mà bạn cần:"

*ReverseVec> :t \k => plusCommutative 1 k \k => plusCommutative 1 k : (k : Nat) -> S k = plus k 1

Bạn có thể coi kiểu của biểu thức này như một "quy tắc viết lại" cho phép bạn thay thế một giá trị bằng giá trị khác. Nếu bạn có thể tìm ra cách áp dụng quy tắc này để viết lại kiểu mong đợi thành Vect (cộng k 1) a, bạn sẽ có thể hoàn thành định nghĩa.

8.2.3.
The rewrite construct: rewriting a type using equality

Chúng ta sẽ tiếp tục định nghĩa myReverse tại điểm sau, sử dụng let để đặt tên cho kết quả mà chúng ta muốn trả về:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = let result = myReverse xs ++ [x] in ?myReverse_rhs_2

Ở giai đoạn này, đây là các loại:

 elem : Type x : elem k : Nat xs : Vect k elem result : Vect (plus k 1) elem -------------------------------------- myReverse_rhs_2 : Vect (S k) elem

Để hoàn thành định nghĩa, bạn có thể sử dụng thông tin do plus-Commutative 1 k cung cấp để viết lại kiểu của ?myReverse_rhs_2. Bạn sẽ muốn thay thế bất kỳ S k nào trong kiểu của ?myReverse_rhs_2 bằng plus k 1, để bạn có thể trả về kết quả. Idris cung cấp một cú pháp để sử dụng các chứng minh về sự đồng nhất nhằm viết lại các kiểu, như được minh họa trong hình 8.1.

Figure 8.1.
Rewriting a type using an equality proof

Vì vậy, bạn có thể triển khai myReverse bằng cách sử dụng cấu trúc rewrite để cập nhật kiểu của ?myReverse_rhs_2, thực hiện các bước sau:

Define— Before rewriting the type using plusCommutative 1 k, you’ll need to bring k into scope, and k arises from pattern matching on the length of the input vector:
```
myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse {n = S k} (x :: xs) = let result = myReverse xs ++ [x] in ?myReverse_rhs_2
```

Refine, type— Now, you can apply the rewriting rule:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse {n = S k} (x :: xs) = let result = myReverse xs ++ [x] in rewrite plusCommutative 1 k in ?myReverse_rhs_2

If you look at the resulting type for ?myReverse_rhs_2, you can see the effect the rewrite has had:

 elem : Type k : Nat x : elem xs : Vect k elem result : Vect (plus k 1) elem _rewrite_rule : plus k 1 = S k -------------------------------------- myReverse_rhs_2 : Vect (plus k 1) elem

Refine— Finally, you can complete the definition using expression search:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse {n = S k} (x :: xs) = let result = myReverse xs ++ [x] in rewrite plusCommutative 1 k in result

Bằng cách sử dụng rewrite, bạn đã thay thế một biểu thức trong kiểu (S k) bằng một biểu thức tương đương (plus k 1), điều này cho phép bạn sử dụng kết quả. Nhưng mặc dù điều này đã cho phép bạn viết hàm, định nghĩa này vẫn còn thiếu sót: phần của định nghĩa tính toán kết quả (myReverse xs ++ [x]) đã trở nên khá mờ nhạt trong chi tiết của chứng minh. Bạn có thể cải thiện điều này bằng cách ủy thác chi tiết của chứng minh, sử dụng một khoảng trống.

8.2.4.
Delegating proofs and rewriting to holes

Thay vì áp dụng việc viết lại bên trong định nghĩa của myReverse, bạn có thể sử dụng một chỗ trống cùng với chỉnh sửa tương tác để tạo ra một hàm trợ giúp chứa các chi tiết của chứng minh. Hãy bắt đầu lại, với định nghĩa ban đầu (thất bại) của myReverse:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = myReverse xs ++ [x]

Bạn có thể sửa định nghĩa này bằng cách sử dụng các bước sau:

Refine, type— Add a hole to the right side, which takes the initial attempt as an argument:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = ?reverseProof (myReverse xs ++ [x])

If you check the type of ?reverseProof, you’ll see exactly how you need to rewrite the type for this definition to be accepted:

 elem : Type x : elem k : Nat xs : Vect k elem -------------------------------------- reverseProof : Vect (plus k 1) elem -> Vect (S k) elem

Type—

Using Ctrl-Alt-L in Atom, lift ?reverseProof to a top-level function:

reverseProof : (x : elem) -> (xs : Vect k elem) -> Vect (k + 1) elem -> Vect (S k) elem myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = reverseProof x xs (myReverse xs ++ [x])

Define— Define reverseProof as follows, using the same application of rewrite as in your previous definition of myReverse:

reverseProof : (x : elem) -> (xs : Vect k elem) -> Vect (k + 1) elem -> Vect (S k) elem reverseProof {k} x xs result = rewrite plusCommutative 1 k in result

Refine— Finally, because you don’t use x or xs in reverseProof, and because reverseProof will only be used by myReverse, you can tidy up the definition as follows:

myReverse : Vect n elem -> Vect n elem myReverse [] = [] myReverse (x :: xs) = reverseProof (myReverse xs ++ [x]) where reverseProof : Vect (k + 1) elem -> Vect (S k) elem reverseProof {k} result = rewrite plusCommutative 1 k in result

Bằng cách giới thiệu lỗ ?reverseProof, bạn đã có thể giữ phần tính toán liên quan của myReverse tách biệt khỏi các chi tiết của chứng minh.

8.2.5.
Appending vectors, revisited

Bạn thường có thể tránh được nhu cầu viết lại kiểu bằng cách cẩn thận trong cách bạn viết các kiểu hàm. Ví dụ, trong chương 4, bạn đã thấy cách xác định một hàm nối các vector với kiểu sau:

append : Vect n elem -> Vect m elem -> Vect (n + m) elem

Thứ tự của các đối số cho toán tử + trong kiểu trả về hóa ra là quan trọng do định nghĩa của +. Nếu bạn bắt đầu triển khai điều này (trong tệp AppendVec.idr) bằng cách tạo một định nghĩa khung và sau đó phân tách trường hợp dựa trên đối số đầu tiên, bạn sẽ đạt được trạng thái sau:

append : Vect n elem -> Vect m elem -> Vect (n + m) elem append [] ys = ?append_rhs_1 append (x :: xs) ys = ?append_rhs_2

Sau đó, nếu bạn kiểm tra kiểu của ?append_rhs_1, bạn sẽ thấy như sau:

 elem : Type m : Nat ys : Vect m elem -------------------------------------- append_rhs_1 : Vect m elem

Trong trường hợp này, đối số đầu tiên, [], có kiểu Vect 0 elem, và đối số thứ hai, ys, có kiểu Vect m elem. Theo kiểu trả về của hàm append, ?append_rhs_1 nên có kiểu Vect (0 + m) elem, điều này giảm về Vect m elem theo định nghĩa của +.

Hãy xem điều gì xảy ra nếu bạn hoán đổi các đối số n và m như sau:

append : Vect n elem -> Vect m elem -> Vect (m + n) elem append [] ys = ?append_rhs_1 append (x :: xs) ys = ?append_rhs_2

Bạn hiện đang thấy một loại khác cho ?append_rhs_1:

 elem : Type m : Nat ys : Vect m elem -------------------------------------- append_rhs_1 : Vect (plus m 0) elem

Như trong định nghĩa của myReverse, Idris không thể rút gọn plus m 0 thêm nữa, vì plus được định nghĩa bằng cách khớp mẫu dựa trên đối số đầu tiên của nó, và hình thức của m là không xác định. Vì lý do này, bạn không thể đơn giản trả về ys cho trường hợp này, và bạn sẽ cần phải viết lại kiểu của append_rhs_1. Bạn sẽ gặp vấn đề tương tự cho append_rhs_2; danh sách bên dưới cho thấy định nghĩa của append, với các chỗ trống thay cho các viết lại cần thiết.

Listing 8.6.
Implementing `append` on vectors with the arguments to `+` swapped in the return type (AppendVec.idr)

Danh sách tiếp theo hiển thị một định nghĩa hoàn chỉnh của hàm append, với định nghĩa của append_nil và append_xs mà viết lại các kiểu cho từng trường hợp.

Listing 8.7.
Completing `append` on vectors by adding rewriting proofs for `append_nil` and `append_xs` (AppendVec.idr)

Các bản viết lại này sử dụng một số định nghĩa từ Prelude. Hai trong số đó hỗ trợ việc viết lại các biểu thức sử dụng Nat:

plusZeroRightNeutral : (left : Nat) -> left + 0 = left plusSuccRightSucc : (left : Nat) -> (right : Nat) -> S (left + right) = left + S right

Thứ ba, sym cho phép bạn áp dụng một quy tắc viết lại theo chiều ngược lại:

sym : left = right -> right = left

Về cơ bản, plusZeroRightNeutral và plusSuccRightSucc cùng nhau giải thích rằng hành vi của plus là giống hệt nhau nếu các đối số được đưa ra theo thứ tự ngược lại.

Exercises

Using plusZeroRightNeutral and plusSuccRightSucc, write your own version of plusCommutes:
```
myPlusCommutes : (n : Nat) -> (m : Nat) -> n + m = m + n
```
Hint: Write this by case splitting on n. In the case of S k, you can rewrite with a recursive call to myPlusCommutes k m, and rewrites can be nested.
The implementation of myReverse you wrote earlier is inefficient because it needs to traverse the entire vector to append a single element on every iteration. You can write a better definition as follows, using a helper function, reverse', that takes an accumulating argument to build the reversed list:
```
myReverse : Vect n a -> Vect n a myReverse xs = reverse' [] xs where reverse' : Vect n a -> Vect m a -> Vect (n+m) a reverse' acc [] = ?reverseProof_nil acc reverse' acc (x :: xs) = ?reverseProof_xs (reverse' (x::acc) xs)
```
Complete this definition by implementing the holes ?reverseProof_nil and ?reverseProof_xs. You can test your answer at the REPL as follows:
```
*ex_8_2> myReverse [1,2,3,4] [4, 3, 2, 1] : Vect 4 Integer
```

8.3. The empty type and decidability

Bạn có thể sử dụng loại equality, =, để viết các hàm với các loại cho biết rằng hai giá trị được đảm bảo là bằng nhau, và sau đó sử dụng đảm bảo này ở nơi khác trong chương trình. Điều này hoạt động vì cách duy nhất để xây dựng một giá trị với loại equality là sử dụng Refl, và Refl chỉ xây dựng một giá trị với loại có dạng x = x:

Idris> :t Refl Refl : x = x Idris> Refl {x = 94} Refl : 94 = 94

Nhưng nếu bạn muốn nói ngược lại, rằng hai giá trị được đảm bảo là không bằng nhau thì sao? Khi bạn tạo ra một giá trị trong một kiểu dữ liệu, bạn đang đưa ra bằng chứng rằng một phần tử của kiểu đó tồn tại. Để chứng minh rằng hai giá trị x và y không bằng nhau, bạn cần có thể cung cấp bằng chứng rằng một phần tử của kiểu x = y không thể tồn tại.

Trong phần này, bạn sẽ thấy cách sử dụng kiểu rỗng, Void, để biểu thị rằng điều gì đó là không thể. Nếu một hàm trả về giá trị có kiểu Void, điều đó chỉ có thể có nghĩa là không thể tạo ra giá trị từ các đầu vào của nó (hoặc, về mặt logic, rằng các kiểu của đầu vào của nó biểu thị một mâu thuẫn.) Chúng ta sẽ sử dụng Void để biểu thị các đảm bảo trong các kiểu rằng các giá trị không thể bằng nhau, và sau đó sử dụng nó để viết một kiểu chính xác hơn cho checkEqNat, điều này đảm bảo rằng

If its inputs are equal, it will produce a proof that they are equal
If its inputs are not equal, it will produce a proof that they are not equal

Đầu tiên, hãy cùng xem cách Void được định nghĩa và sử dụng trong trường hợp đơn giản nhất.

8.3.1.
Void: a type with no values

Để biểu thị rằng một điều gì đó không thể xảy ra, Prelude cung cấp một kiểu dữ liệu không có giá trị, đó là Void. Định nghĩa hoàn chỉnh của Void như sau:

data Void : Type where

Bạn không thể viết các giá trị kiểu Void trực tiếp vì không có giá trị nào! Do đó, nếu bạn có một hàm trả về một giá trị kiểu Void, thì điều đó phải vì một trong các tham số của nó cũng không thể được xây dựng.

Cũng giống như bạn có thể sử dụng = để viết các hàm thể hiện các sự thật về cách mà các hàm hoạt động, bạn có thể sử dụng Void để thể hiện các sự thật về cách mà các hàm không hoạt động. Ví dụ, bạn có thể chỉ ra rằng 2 + 2 không bằng 5.

Hãy viết một hàm trong tệp có tên là Void.idr:

Type— Begin by writing the appropriate type:
```
twoPlusTwoNotFive : 2 + 2 = 5 -> Void
```
You can read this “if 2 + 2 = 5, then return an element of the empty type.”

Define— Adding a skeleton definition gives you this:

twoPlusTwoNotFive : 2 + 2 = 5 -> Void twoPlusTwoNotFive prf = ?twoPlusTwoNotFive_rhs

If you look at the type of prf, you’ll see that it’s a proof that 4 = 5:

 prf : 4 = 5 -------------------------------------- twoPlusTwoNotFive_rhs : Void

Define—
You can try to define the function by a case split on prf. Idris produces this:
```
twoPlusTwoNotFive : 2 + 2 = 5 -> Void twoPlusTwoNotFive Refl impossible
```

Định nghĩa này bây giờ đã hoàn chỉnh. Idris đã đưa ra một trường hợp và nhận thấy rằng đầu vào duy nhất có thể, Refl, sẽ không bao giờ hợp lệ. Nhớ lại từ chương 4 rằng từ khóa impossible có nghĩa là điều kiện mẫu không được kiểm tra kiểu.

Void and total functions

Điều quan trọng là phải kiểm tra xem một hàm trả về Void có phải là một hàm tổng quát hay không, nếu bạn thực sự muốn tin rằng nó nhận một đầu vào không thể xảy ra.

*Void> :total twoPlusTwoNotFive Main.twoPlusTwoNotFive is Total

Ngược lại, bạn có thể viết một hàm tuyên bố sẽ trả về Void bằng cách lặp vô hạn:

loop : Void loop = loop

Chức năng này không toàn diện, vì vậy bạn không thể tin rằng nó thực sự tạo ra một phần tử của Void. Idris báo cáo như sau:

*Void> :total loop Main.loop is possibly not total due to recursive path: Main.loop

Tương tự, bạn có thể viết một hàm cho thấy rằng một số không bao giờ có thể bằng số kế tiếp của nó:

valueNotSuc : (x : Nat) -> x = S x -> Void valueNotSuc _ Refl impossible

"Nếu bạn có thể cung cấp một giá trị của kiểu trống, bạn sẽ có thể tạo ra giá trị của bất kỳ kiểu nào. Nói cách khác, nếu bạn có một chứng minh rằng một giá trị không thể xảy ra đã xảy ra, bạn có thể làm bất cứ điều gì. Prelude cung cấp một hàm, void, để diễn đạt điều này:"

void : Void -> a

Có thể sẽ có vẻ kỳ lạ và ít hữu ích thực tiễn khi viết các hàm chỉ để cho thấy rằng một điều gì đó không thể xảy ra. Nhưng nếu bạn biết rằng một điều gì đó không thể xảy ra, bạn có thể sử dụng kiến thức này để diễn đạt những hạn chế về những gì có thể xảy ra. Nói cách khác, bạn có thể diễn đạt một cách chính xác hơn về những gì mà một hàm được dự kiến thực hiện.

8.3.2.
Decidability: checking properties with precision

Trước đây, khi bạn viết checkEqNat, bạn đã sử dụng Maybe cho kết quả:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (num1 = num2)

Vì vậy, nếu checkEqNat trả về một giá trị có dạng Just p, bạn có thể chắc chắn rằng num1 và num2 là bằng nhau, và p đại diện cho một chứng minh rằng chúng bằng nhau. Nhưng bạn không thể nói ngược lại: rằng nếu checkEqNat trả về Nothing, thì num1 và num2 được đảm bảo không bằng nhau.

Định nghĩa sau đây sẽ, chẳng hạn, hoàn toàn hợp lệ, mặc dù không rất hữu ích:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Maybe (num1 = num2) checkEqNat num1 num2 = Nothing

Thay vào đó, để làm cho loại này chính xác hơn, bạn cần một cách để tuyên bố rằng với bất kỳ cặp số nào, num1 và num2, bạn sẽ luôn có thể sản xuất hoặc một bằng chứng rằng chúng bằng nhau (có loại num1 = num2) hoặc một bằng chứng rằng chúng không bằng nhau (có loại num1 = num2 -> Void). Nói cách khác, bạn muốn tuyên bố rằng việc kiểm tra xem num1 = num2 có phải là một thuộc tính quyết định hay không.

Decidability

Một thuộc tính của một số giá trị là có thể quyết định được nếu bạn luôn có thể nói xem thuộc tính đó có tồn tại hay không cho các giá trị cụ thể. Ví dụ, kiểm tra sự bình đẳng trên tập số tự nhiên là có thể quyết định, bởi vì với bất kỳ hai số tự nhiên nào, bạn luôn có thể quyết định xem chúng có bằng nhau hay không.

Danh sách 8.8 cho thấy kiểu tổng quát Dec, được định nghĩa trong Prelude. Giống như Maybe, Dec có một hàm dựng (Yes) mang theo một giá trị. Không giống như Maybe, nó còn có một hàm dựng (No) mang theo một chứng minh rằng không có giá trị nào của kiểu đối số của nó có thể tồn tại.

Listing 8.8.
`Dec`: precisely stating that a property is decidable

Ví dụ, bạn có thể xây dựng một chứng minh rằng 2 + 2 = 4, vì vậy bạn sẽ sử dụng Có:

*Void> the (Dec (2 + 2 = 4)) (Yes Refl) Yes Refl : Dec (4 = 4)

Nhưng thật là không thể xây dựng một chứng minh rằng 2 + 2 = 5, vì vậy bạn sẽ chọn Không và cung cấp chứng cứ của mình, twoPlusTwoNotFive, rằng điều đó là không thể:

*Void> the (Dec (2 + 2 = 5)) (No twoPlusTwoNotFive) No twoPlusTwoNotFive : Dec (4 = 5)

Hãy viết lại checkEqNat sử dụng Dec thay vì Maybe cho kiểu kết quả. Trong quá trình làm như vậy, chúng ta sẽ có hai đảm bảo được trình biên dịch Idris kiểm tra.

If the inputs num1 and num2 are equal, checkEqNat is guaranteed to produce a result of the form Yes prf, where prf has type num1 = num2.
If the inputs num1 and num2 are not equal, checkEqNat is guaranteed to produce a result of the form No contra, where contra has type num1 = num2 -> Void.

Đây là những đảm bảo vì loại checkEqNat tạo ra một liên kết trực tiếp giữa các đầu vào và kiểu đầu ra:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Dec (num1 = num2)

Bạn có thể viết hàm này một cách tương tác, trong một tệp mới có tên là CheckEqDec.idr:

Define, refine— You can mostly follow the same steps as earlier, when you defined checkEqNat using Maybe. But instead of Just, use Yes, and instead of Nothing, use No. No requires proofs that the inputs are unequal, so you can leave holes for these for the moment:

checkEqNat : (num1 : Nat) -> (num2 : Nat) -> Dec (num1 = num2) checkEqNat Z Z = Yes Refl checkEqNat Z (S k) = No ?zeroNotSuc checkEqNat (S k) Z = No ?sucNotZero checkEqNat (S k) (S j) = case checkEqNat k j of Yes prf => Yes (cong prf) No contra => No ?noRec

You can test this at the REPL, even without the proofs, though you may see holes in the results:

*CheckEqDec> checkEqNat 3 3 Yes Refl : Dec (3 = 3) *CheckEqDec> checkEqNat 3 4 No ?noRec : Dec (3 = 4) *CheckEqDec> checkEqNat 3 0 No ?sucNotZero : Dec (3 = 0)

Type— If you look at the types of the holes, you’ll see what you need to prove to complete the definition, as in this example:
```
 k : Nat -------------------------------------- zeroNotSuc : (0 = S k) -> Void
```
Define, refine— You can lift ?zeroNotSuc and ?sucNotZero to top-level definitions with Ctrl-Alt-L and implement them using case splitting and impossible, as with twoPlusTwoNotFive in the previous section, because it’s never possible for zero to be equal to a nonzero number:
```
zeroNotSuc : (0 = S k) -> Void zeroNotSuc Refl impossible sucNotZero : (S k = 0) -> Void sucNotZero Refl impossible
```
Type, define—
For ?noRec, you can take a look at the type to see what you need to show:
```
 k : Nat j : Nat contra : (k = j) -> Void -------------------------------------- noRec : (S k = S j) -> Void
```
The type of contra tells you that k is guaranteed not to be equal to j. Given that, you have to show that S k can’t equal S j. Again, you can lift this to a top-level definition with Ctrl-Alt-L:
```
noRec : (contra : (k = j) -> Void) -> (S k = S j) -> Void noRec contra prf = ?noRec_rhs
```
Define— The type of noRec says that if you have a proof that k = j is impossible, and a proof that S k = S j, you can produce an element of the empty type. Logically, the two inputs contradict each other. You can write this function by case splitting on prf:
```
noRec : (contra : (k = j) -> Void) -> (S k = S j) -> Void noRec contra Refl = ?noRec_rhs_1
```
Type— The only possible value prf can take is Refl, and the only way it can take the value Refl is if S k and S j are equal, and therefore k and j are equal. Recognizing this, Idris refines the type of contra, as you can see by inspecting the type of noRec_rhs_1:
```
 j : Nat contra : (j = j) -> Void -------------------------------------- noRec_rhs_1 : Void
```
Refine— To complete the definition, you can use contra to produce an element of the empty type; an expression search will find this:
```
noRec : (contra : (k = j) -> Void) -> (S k = S j) -> Void noRec contra Refl = contra Refl
```

Danh sách sau đây hiển thị định nghĩa đầy đủ của checkEqNat, bao gồm các hàm trợ giúp zeroNotSuc, sucNotZero và noRec.

Listing 8.9.
Checking whether `Nat`s are equal, with a precise type (CheckEqDec.idr)

Proving inputs are impossible with Void

Khi bạn chạy checkEqNat, bạn thực sự không thể tạo ra một giá trị của kiểu trống bằng cách sử dụng zeroNotSuc, sucNotZero hoặc noRec. Về cơ bản, một hàm sản xuất một giá trị của kiểu Void có thể được coi là một chứng minh rằng các tham số của nó không thể được cung cấp cùng một lúc. Trong trường hợp của noRec, kiểu của các hàm cho biết rằng nếu bạn có thể cung cấp cả một chứng minh rằng k không bằng j và một chứng minh rằng S k = S j, thì sẽ có một mâu thuẫn, và do đó bạn có thể có một giá trị của kiểu Void.

Bằng cách sử dụng Dec, bạn đã có thể viết rõ ràng trong kiểu dữ liệu những gì checkEqNat được dự kiến thực hiện: trả về hoặc một bằng chứng rằng các đầu vào là bằng nhau hoặc một bằng chứng rằng chúng không bằng nhau. Tuy nhiên, lợi ích thực sự của điều này không nằm ở checkEqNat mà ở các hàm sử dụng nó, vì chúng không chỉ có kết quả của bài kiểm tra sự bằng nhau, mà còn có một bằng chứng rằng bài kiểm tra sự bằng nhau đã hoạt động chính xác.

Việc đảm bảo rằng hai giá trị là bằng nhau (hoặc khác nhau) thường rất hữu ích trong phát triển dựa trên kiểu, vì việc chỉ ra mối quan hệ giữa các cấu trúc lớn hơn phụ thuộc vào việc chỉ ra mối quan hệ giữa các thành phần riêng lẻ. Do đó, Idris Prelude cung cấp một giao diện, DecEq, với một hàm tổng quát, decEq, để quyết định tính chất bằng nhau.

8.3.3.
DecEq: an interface for decidable equality

Thay vì cung cấp các hàm cụ thể như checkEqNat cho mỗi loại, Prelude của Idris cung cấp một giao diện, DecEq. Danh sách tiếp theo cho thấy cách DecEq được định nghĩa. Có các triển khai cho tất cả các loại được định nghĩa trong Prelude.

Listing 8.10.
The `DecEq` interface (defined in the Prelude)

Thay vì định nghĩa và sử dụng một hàm chuyên dụng, checkEqNat, để định nghĩa exact-Length, bạn có thể sử dụng decEq. Danh sách dưới đây cho thấy cách thực hiện điều này, và đây là định nghĩa của exactLength được sử dụng trong Data.Vect.

Listing 8.11.
Implementing `exactLength` using `decEq` (ExactLengthDec.idr)

exactLength : (len : Nat) -> (input : Vect m a) -> Maybe (Vect len a) exactLength {m} len input = case decEq m len of Yes Refl => Just input No contra => Nothing

Sử dụng decEq thay vì toán tử so sánh Boolean, ==, sẽ cung cấp cho bạn một đảm bảo mạnh mẽ về cách thức kiểm tra sự bằng nhau hoạt động. Bạn có thể chắc chắn rằng nếu decEq trả về giá trị dạng Yes prf, thì các đầu vào thật sự bằng nhau về cấu trúc.

Trong chương tiếp theo, bạn sẽ thấy cách mô tả mối quan hệ giữa các cấu trúc dữ liệu lớn hơn (chẳng hạn như chỉ ra rằng một giá trị là phần tử của một danh sách) và cách sử dụng decEq để xây dựng các chứng minh cho những mối quan hệ này.

Exercises

Implement the following functions:

headUnequal : DecEq a => {xs : Vect n a} -> {ys : Vect n a} -> (contra : (x = y) -> Void) -> ((x :: xs) = (y :: ys)) -> Void tailUnequal : DecEq a => {xs : Vect n a} -> {ys : Vect n a} -> (contra : (xs = ys) -> Void) -> ((x :: xs) = (y :: ys)) -> Void

The first states that if the first elements of two vectors are unequal, then the vectors must be unequal. The second states that if there are differences in the tails of two vectors, then the vectors must be unequal. If you have a correct solution, both headUnequal and tailUnequal should type-check and be total:

*ex_8_3> :total headUnequal Main.headUnequal is Total *ex_8_3> :total tailUnequal Main.tailUnequal is Total

Implement DecEq for Vect. Begin with the following implementation header:
```
DecEq a => DecEq (Vect n a) where
```
Hint: You’ll find headUnequal and tailUnequal useful here. Remember to check the types of the holes as you write the definition. You should also use your own definition of Vect rather than importing Data.Vect, because the library provides a DecEq implementation. You can test your answer at the REPL as follows:
```
*ex_8_3> decEq (the (Vect _ _) [1,2,3]) [1,2,3] Yes Refl : Dec ([1, 2, 3] = [1, 2, 3])
```

8.4. Summary

You can write a type to express a proof that two values must be equal.
You can write functions that take equality types as inputs to prove additional properties of data.
Using Maybe, you can test for equality of values at runtime.
The generic = type allows you to describe equality between values of any type.
Proof requirements arise naturally when programming with dependent types, such as to show that lengths are preserved when reversing a vector.
The rewrite construct allows you to update a type using an equality proof.
Using holes and interactive editing, you can delegate the details of rewriting types to a separate function.
Void is a type with no values, used to show that inputs to a function can’t all occur at once.
A property is decidable if you can always say whether the property holds for some specific values.
Using Dec, you can compute at runtime whether a property is guaranteed to hold or guaranteed not to hold.

Chapter 9.
Predicates: expressing assumptions and contracts in types

Chương này đề cập đến

Describing and checking membership of a vector using a predicate
Using predicates to describe contracts for function inputs and outputs
Reasoning about system state in types

Các kiểu phụ thuộc như EqNat và =, mà bạn đã thấy trong chương trước, được sử dụng hoàn toàn để mô tả các mối quan hệ giữa dữ liệu. Những kiểu này thường được gọi là các tiên đề, đây là các kiểu dữ liệu tồn tại hoàn toàn để mô tả một thuộc tính của một số dữ liệu. Nếu bạn có thể xây dựng một giá trị cho một tiên đề, thì bạn biết rằng thuộc tính được mô tả bởi tiên đề đó phải đúng.

Trong chương này, bạn sẽ thấy cách biểu thị các mối quan hệ phức tạp hơn giữa dữ liệu bằng cách sử dụng các điều kiện. Bằng cách biểu diễn mối quan hệ giữa dữ liệu trong các kiểu, bạn có thể nêu rõ những giả định mà bạn đang đưa ra về đầu vào của một hàm, và những giả định đó sẽ được bộ kiểm tra kiểu kiểm tra khi các hàm đó được gọi. Bạn thậm chí có thể coi những giả định này như là những hợp đồng thời biên mà các đối số khác phải đáp ứng trước khi bất kỳ điều gì có thể gọi hàm.

Trên thực tế, bạn sẽ thường viết các hàm mà đưa ra giả định về hình thức của một số dữ liệu khác, với hy vọng đã kiểm tra những giả định đó trước đó. Dưới đây là một vài ví dụ:

A function that reads from a file assumes that the file handle describes an open file.
A function that processes data it has received from a network assumes that the data follows the appropriate protocol.
A function that retrieves user data (say, for a customer on a website) assumes that the user has successfully authenticated.

Bạn cần đảm bảo rằng bạn kiểm tra bất kỳ giả định cần thiết nào trước khi gọi các hàm này, đặc biệt khi an ninh hoặc quyền riêng tư của người dùng bị ảnh hưởng. Trong Idris, bạn có thể làm cho loại giả định này trở nên rõ ràng trong kiểu, và để trình biên dịch kiểu đảm bảo rằng bạn đã kiểm tra đúng giả định trước đó. Một lợi thế của việc biểu thị các giả định trong kiểu là chúng được đảm bảo sẽ đúng, ngay cả khi hệ thống phát triển theo thời gian.

Trong chương này, chúng ta sẽ xem xét một ví dụ nhỏ một cách sâu sắc: loại bỏ một giá trị khỏi một vector nếu giá trị đó có trong vector. Chúng ta sẽ tìm hiểu cách diễn đạt trong một kiểu mà một vector chứa một phần tử cụ thể, cách kiểm tra thuộc tính này tại thời gian chạy, và cách sử dụng những thuộc tính như vậy trong thực tế để viết một chương trình lớn hơn với một số khía cạnh hành vi của nó được biểu diễn trong kiểu dữ liệu của nó.

9.1. Membership tests: the Elem predicate

Sử dụng =, Void và Dec, bạn có thể mô tả các thuộc tính mà chương trình của bạn thỏa mãn trong các kiểu, làm cho các kiểu trở nên chính xác hơn. Thông thường, bạn sẽ sử dụng =, Void và Dec như những khối xây dựng để mô tả và kiểm tra mối quan hệ giữa các phần dữ liệu. Mô tả mối quan hệ trong các kiểu cho phép bạn nêu ra các giả định mà các hàm thực hiện và, quan trọng hơn, nó cho phép Idris kiểm tra xem những giả định đó có được thỏa mãn hay vi phạm.

Ví dụ, bạn có thể muốn

Remove an element from a vector only under the assumption that the element is present in the vector
Search for a value in a list only under the assumption that the list is ordered
Run a database query only under the assumption that the inputs have been validated
Send a message to a machine on the network only under the assumption that you have an open connection

Trong phần này, chúng ta sẽ xem xét cái đầu tiên trong số này một cách chi tiết hơn. Chúng ta sẽ bắt đầu bằng cách cố gắng viết một hàm để loại bỏ một phần tử khỏi một vector, và sau đó chúng ta sẽ xem cách tinh chỉnh kiểu dữ liệu để khẳng định và kiểm tra bất kỳ giả định cần thiết nào làm cho kiểu dữ liệu chính xác hơn. Cuối cùng, chúng ta sẽ sử dụng hàm trong một chương trình tương tác đơn giản.

9.1.1.
Removing an element from a Vect

Nếu bạn có một Vect chứa một số phần tử, bạn sẽ mong đợi điều sau từ một hàm removeElem để xóa một phần tử cụ thể khỏi vector đó:

The input vector should have at least one element.
The output vector’s length should be one less than the input vector’s length.

Bởi vì Vect được tham số hóa bởi kiểu phần tử chứa trong vector và được lập chỉ mục bởi độ dài của vector, bạn có thể (trên thực tế, bạn phải) biểu diễn các thuộc tính độ dài này trong kiểu của removeElem. Cố gắng đầu tiên của bạn có thể trông như thế này:

removeElem : (value : a) -> (xs : Vect (S n) a) -> Vect n a

Hãy xem điều gì sẽ xảy ra nếu bạn cố gắng viết chức năng này:

Define— If you add a skeleton definition and case-split on xs, Idris will give you only one pattern, because xs can’t be an empty vector:
```
removeElem : (value : a) -> (xs : Vect (S n) a) -> Vect n a removeElem value (x :: xs) = ?removeElem_rhs_1
```
Refine— If the value you’re looking for is equal to x, you can remove it from the list, returning xs. You’ll need to refine the type before you can compare value and x; you can use decidable equality so that you can be certain that the equality test is accurate. This is the refined type:
```
removeElem : DecEq a => (value : a) -> (xs : Vect (S n) a) -> Vect n a
```

Refine— You can now use decEq to compare value and x, and discard x if they’re equal:

removeElem : DecEq a => (value : a) -> (xs : Vect (S n) a) -> Vect n a removeElem value (x :: xs) = case decEq value x of Yes prf => xs No contra => ?removeElem_rhs_3

Refine failure—For ?removeElem_rhs_3, you might hope to be able to remove value from xs recursively, but if you try this, you’ll get an error:
```
removeElem : DecEq a => (value : a) -> (xs : Vect (S n) a) -> Vect n a removeElem value (x :: xs) = case decEq value x of Yes prf => xs No contra => x :: removeElem value xs
```
Idris reports the following:
```
When checking right hand side of Main.case block in removeElem at removeelem.idr:4:35 with expected type Vect n a When checking argument xs to Main.removeElem: Type mismatch between Vect n a (Type of xs) and Vect (S k) a (Expected type)
```
The problem is that removeElem requires a vector that’s guaranteed to be non-empty, but xs may be empty! You can see this from its type, Vect n a: the n could stand for any natural number, including zero. This problem arises because there’s no guarantee that value will appear in the vector, so it’s possible to reach the end of the vector without encountering it. If this happens, there’s no value to remove, so you can’t satisfy the type. You’ll need to refine the type further in order to be able to write this function. You can try one of the following:
- Rewrite the type so that removeElem returns Maybe (Vect n a), returning Nothing if the value doesn’t appear in the input.
- Rewrite the type so that removeElem returns a dependent pair, (newLength ** Vect newLength a).
- Express a precondition on removeElem that the value is guaranteed to be in the vector.

Bạn đã thấy cách diễn đạt sự thất bại có thể xảy ra với Maybe (trong chương 4), và cách diễn đạt một độ dài không xác định bằng các cặp phụ thuộc (trong chương 5). Tuy nhiên, tùy chọn thứ ba sẽ diễn đạt chính xác mục đích của removeElem. Để đạt được điều này, bạn sẽ cần viết một kiểu dữ liệu mô tả mối quan hệ giữa một giá trị và một vector chứa giá trị đó.

Nếu bạn có thể mô tả theo một kiểu mà một vector chứa một phần tử cụ thể, bạn sẽ có thể sử dụng kiểu đó để biểu thị một hợp đồng cho hàm removeElem, cho thấy rằng bạn chỉ có thể sử dụng nó nếu bạn biết phần tử đó có trong vector. Trong phần còn lại của phần này, bạn sẽ triển khai kiểu này, Elem, sử dụng nó để làm cho kiểu của removeElem chính xác hơn, và tìm hiểu thêm về cách sử dụng Elem trong thực tế.

9.1.2.
The Elem type: guaranteeing a value is in a vector

Trong chương trước, bạn đã thấy cách diễn đạt rằng hai giá trị được đảm bảo là bằng nhau bằng cách sử dụng loại EqNat cụ thể hoặc loại tổng quát =. Sự tồn tại của một giá trị trong một trong những loại này về cơ bản là một chứng minh rằng hai giá trị bằng nhau. Bạn có thể làm điều tương tự để đảm bảo rằng một giá trị nằm trong một vector.

Mục tiêu của chúng tôi là định nghĩa một kiểu, Elem, với cấu trúc kiểu sau:

Elem : (value : a) -> (xs : Vect k a) -> Type

Nếu chúng ta có một giá trị, và một vector, xs, chứa giá trị đó, chúng ta nên có khả năng xây dựng một phần tử của kiểu Elem value xs. Ví dụ, chúng ta nên có khả năng xây dựng các phần tử sau:

oneInVector : Elem 1 [1,2,3] maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"]

Chúng ta cũng nên có khả năng xây dựng các hàm của các loại sau, cho thấy rằng một giá trị cụ thể không có trong một vector:

fourNotInVector : Elem 4 [1,2,3] -> Void peteNotInVector : Elem "Pete" ["John", "Paul", "George", "Ringo"] -> Void

Danh sách dưới đây cho thấy cách kiểu dữ liệu phụ thuộc Elem được định nghĩa trong Data.Vect.

Listing 9.1.
The `Elem` dependent type, expressing that a value is guaranteed to be contained in a vector (defined in Data.Vect)

Giá trị ở đây có thể được xem như một bằng chứng rằng giá trị đó là giá trị đầu tiên trong một vector, như trong ví dụ này:

oneInVector : Elem 1 [1,2,3] oneInVector = Here

Bộ khởi tạo There, với một đối số cho thấy giá trị x nằm trong vector xs, có thể được hiểu như một bằng chứng rằng x cũng phải nằm trong vector y :: xs cho bất kỳ giá trị y nào.

Để minh họa điều này, hãy thử viết maryInVector:

maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"]

Define— Create a skeleton definition with a hole for the right side:

maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"] maryInVector = ?maryInVector_rhs

Refine, type—You can’t use Here, because "Mary" isn’t the first element of the vector, so try using There and leaving a hole for its argument:
```
maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"] maryInVector = There ?maryInVector_rhs
```
If you check the type of ?maryInVector_rhs, you’ll see that you now have a smaller problem:
```
-------------------------------------- maryInVector_rhs : Elem "Mary" ["Paul", "Mary"]
```

Refine, type—If you do the same again, applying There and leaving a hole for its argument, you get the following program:

maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"] maryInVector = There (There ?maryInVector_rhs)

You also now have a simpler type for ?maryInVector_rhs:

-------------------------------------- maryInVector_rhs : Elem "Mary" ["Mary"]

Refine—"Mary" is now the first element in the vector, so you can refine ?maryInVector_rhs using Here:
```
maryInVector : Elem "Mary" ["Peter", "Paul", "Mary"] maryInVector = There (There Here)
```

Expression search

Một tìm kiếm biểu thức với Ctrl-Alt-S sẽ thành công trong việc tìm định nghĩa của maryInVector, và nó thường hữu ích để xây dựng các giá trị của các kiểu phụ thuộc như Elem và =.

Bạn có thể sử dụng Elem và các loại tương tự mô tả mối quan hệ giữa dữ liệu để biểu thị các hợp đồng về dạng dữ liệu được mong đợi như đầu vào cho một hàm. Các hợp đồng này, được biểu thị dưới dạng loại, có thể được Idris xác minh thông qua kiểm tra loại; nếu một cuộc gọi hàm vi phạm hợp đồng, chương trình sẽ không biên dịch.

Một cách xây dựng hơn, nếu bạn diễn đạt các loại hàm của mình một cách đủ chính xác, với các hợp đồng được thể hiện bằng các loại như Elem, bạn biết rằng một khi chương trình của bạn biên dịch, mọi hợp đồng đều phải được thỏa mãn. Bạn có thể sử dụng Elem để diễn đạt một hợp đồng cho removeElem mà xác định khi nào các đầu vào là hợp lệ.

9.1.3.
Removing an element from a Vect: types as contracts

Khó khăn mà chúng tôi gặp phải khi viết hàm removeElem là chúng tôi không thể thực hiện gọi đệ quy ở đuôi của vector vì không thể đảm bảo rằng phần tử mà chúng tôi muốn xóa nằm trong vector. Do đó, chúng tôi sẽ tinh chỉnh kiểu của removeElem, thêm một đối số để biểu thị hợp đồng rằng phần tử cần xóa phải có trong vector. Danh sách dưới đây cho thấy điểm khởi đầu của chúng tôi.

Listing 9.2.
Removing an element from a vector, with a contract specified in the type using `Elem` (RemoveElem.idr)

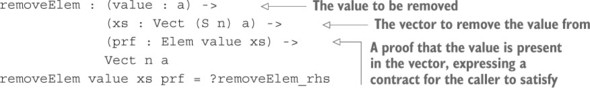
Trong phát triển dựa trên kiểu, chúng tôi hướng đến việc sử dụng các kiểu chính xác hơn để giúp định hướng việc triển khai các hàm. Ở đây, đầu vào prf cung cấp độ chính xác cao hơn cho kiểu đầu vào của hàm removeElem, và bạn thậm chí có thể phân nhánh dựa trên nó để xem những gì bạn có thể học về giá trị của đầu vào và xs từ mối quan hệ được xác định giữa chúng bởi prf.

Bạn có thể viết hàm như sau:

Define— Begin with the case split on prf:

removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ?removeElem_rhs_1 removeElem value (y :: ys) (There later) = ?removeElem_rhs_2

Refine— For the first case, ?removeElem_rhs_1, you can see from the patterns that Idris has generated that value must be the first element in the vector if the proof has the form Here. You can therefore refine this case to remove value:
```
removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ys removeElem value (y :: ys) (There later) = ?removeElem_rhs_2
```
Type— If you look at the type of ?removeElem_rhs_2, you’ll see that it appears you have the same problem as before, in that ys has length n, and removeElem requires a vector of length S n for the recursive call:
```
 a : Type value : a y : a n : Nat ys : Vect n a later : Elem value ys -------------------------------------- removeElem_rhs_2 : Vect n a
```
But you have some further information that you didn’t have available earlier: you know from the variable later that value must occur in ys, and this means that ys must have a nonzero length. But how can you use this knowledge?

Define— Given that the length n must be nonzero, the trick is to case-split on n (by bringing it into scope using braces on the left side of the definition) and show that it’s impossible for it to be zero:

removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ys removeElem {n = Z} value (y :: ys) (There later) = ?removeElem_rhs_1 removeElem {n = (S k)} value (y :: ys) (There later) = ?removeElem_rhs_3

Refine— Now, you can complete ?removeElem_rhs_3. You now know the length of ys is nonzero, so you can make a recursive call:

removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ys removeElem {n = Z} value (y :: ys) (There later) = ?removeElem_rhs_1 removeElem {n = (S k)} value (y :: ys) (There later) = y :: removeElem value ys later

Note that you need to pass later to the recursive call, as evidence that value is contained within ys.

Type, define—For the remaining hole, ?removeElem_rhs_1, take a look at its type and what variables are available:
```
 a : Type value : a y : a ys : Vect 0 a later : Elem value ys -------------------------------------- removeElem_rhs_2 : Vect 0 a
```
You’re looking for an empty vector. That empty vector, if you look at the variables on the left side, should be a vector resulting from removing value from ys. This doesn’t make sense, because ys is an empty vector! You can make this more clear by case splitting on ys. Idris produces only one case:
```
removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ys removeElem {n = Z} value (y :: []) (There later) = ?removeElem_rhs_1 removeElem {n = (S k)} value (y :: ys) (There later) = y :: removeElem value ys later
```
Looking at the type of the new hole, ?removeElem_rhs_1, shows the following:
```
 a : Type value : a y : a later : Elem value [] -------------------------------------- removeElem_rhs_1 : Vect 0 a
```
Previously, you’ve used the impossible keyword to rule out a case that doesn’t type-check. This case does type-check, so you can’t use impossible. But there’s no way you’ll ever have a value of type Elem value [] as an input, because there’s no way to construct an element of this type.
Refine— You can complete the definition using a function, absurd, defined in the Prelude. It has the following type:
```
absurd : Uninhabited t => t -> a
```
The Uninhabited interface, described in the sidebar, can be implemented for any type that has no values (as you saw with twoplustwo_not_five in chapter 8). So, you can refine ?remove_Elem_rhs_1 as follows:
```
removeElem : (value : a) -> (xs : Vect (S n) a) -> (prf : Elem value xs) -> Vect n a removeElem value (value :: ys) Here = ys removeElem {n = Z} value (y :: []) (There later) = absurd later removeElem {n = (S k)} value (y :: ys) (There later) = y :: removeElem value ys later
```

The Uninhabited interface

Nếu một kiểu không có giá trị nào, như 2 + 2 = 5 hoặc Elem x [], bạn có thể cung cấp một triển khai của giao diện Uninhabited cho nó. Uninhabited được định nghĩa trong Prelude như sau:

interface Uninhabited t where uninhabited : t -> Void

Có một phương pháp, trả về một phần tử của kiểu rỗng. Ví dụ, bạn có thể cung cấp một triển khai của Uninhabited cho 2 + 2 = 5:

Uninhabited (2 + 2 = 5) where uninhabited Refl impossible

Sử dụng thuật ngữ "không có người ở", phần Mở đầu định nghĩa "vô lý" như sau, sử dụng "trống rỗng":

absurd : Uninhabited t => (h : t) -> a absurd h = void (uninhabited h)

Tham số bổ sung cho hàm removeElem, có kiểu giá trị Elem xs, có nghĩa là removeElem có thể hoạt động dưới giả định rằng giá trị đó có trong vector xs. Nó cũng có nghĩa là bạn phải cung cấp một bằng chứng rằng giá trị đó có trong xs khi gọi hàm này.

9.1.4.
auto-implicit arguments: automatically constructing proofs

Nếu bạn thử chạy removeElem với một số giá trị cụ thể cho phần tử và vector, bạn sẽ thấy rằng bạn cần cung cấp một tham số bổ sung cho bằng chứng. Đôi khi, đó có thể là một bằng chứng mà bạn có thể xây dựng.

*RemoveElem> removeElem 2 [1,2,3,4,5] removeElem 2 [1, 2, 3, 4, 5] : Elem 2 [1, 2, 3, 4, 5] -> Vect 4 Integer

Đôi khi nó có thể không:

*RemoveElem> removeElem 7 [1,2,3,4,5] removeElem 7 [1, 2, 3, 4, 5] : Elem 7 [1, 2, 3, 4, 5] -> Vect 4 Integer

Trong trường hợp đầu tiên, bạn có thể gọi removeElem bằng cách cung cấp rõ ràng một chứng minh của Elem 2 [1,2,3,4,5]:

*RemoveElem> removeElem 2 [1,2,3,4,5] (There Here) [1, 3, 4, 5] : Vect 4 Integer

Cần cung cấp các chứng minh một cách rõ ràng như thế này có thể tạo ra nhiều tiếng ồn cho các chương trình và có thể gây hại cho khả năng đọc hiểu. Idris cung cấp một loại tham số ngầm định đặc biệt, được đánh dấu bằng từ khóa auto, để giảm bớt tiếng ồn này.

Bạn có thể định nghĩa một hàm removeElem_auto:

removeElem_auto : (value : a) -> (xs : Vect (S n) a) -> {auto prf : Elem value xs} -> Vect n a removeElem_auto value xs {prf} = removeElem value xs prf

Tham số thứ ba, được gọi là prf, là một tham số ẩn tự động. Giống như các tham số ẩn mà bạn đã thấy, một tham số ẩn tự động có thể được đưa vào phạm vi bằng cách viết nó trong ngoặc nhọn, và Idris sẽ cố gắng tự động tìm một giá trị. Khác với các tham số ẩn thông thường, Idris sẽ tìm kiếm một giá trị cho tham số ẩn tự động bằng cách sử dụng cùng một cơ chế mà nó sử dụng cho việc tìm kiếm biểu thức với Ctrl-Alt-S trong Atom.

Khi bạn chạy removeElem_auto với các đối số cho giá trị và xs, Idris sẽ cố gắng xây dựng một chứng minh cho đối số được đánh dấu tự động:

*RemoveElem> removeElem_auto 2 [1,2,3,4,5] [1, 3, 4, 5] : Vect 4 Integer

Nếu không tìm thấy chứng minh, nó sẽ báo lỗi:

*RemoveElem> removeElem_auto 7 [1,2,3,4,5] (input):1:17:When checking argument prf to function Main.removeElem_auto: Can't find a value of type Elem 7 [1, 2, 3, 4, 5]

Ngoài ra, danh sách sau đây cho thấy cách bạn có thể định nghĩa removeElem bằng cách sử dụng một hàm tự động ngầm định trực tiếp.

Listing 9.3.
Defining `removeElem` using an `auto`-implicit argument (RemoveElem.idr)

Nói chung, bạn sẽ không biết các giá trị cụ thể mà bạn đang truyền cho removeElem. Chúng có thể là các giá trị được đọc từ người dùng hoặc được tạo ra bởi một phần khác của chương trình. Do đó, chúng ta cần xem xét cách bạn có thể sử dụng removeElem khi các đầu vào không được biết cho đến lúc chạy.

Cũng giống như bạn đã viết một hàm checkEqNat để quyết định xem hai số có bằng nhau hay không, và sau đó tổng quát hóa nó thành decEq bằng cách sử dụng giao diện, bạn sẽ cần một hàm để quyết định xem một giá trị có nằm trong một vector hay không.

9.1.5.
Decidable predicates: deciding membership of a vector

Như bạn đã thấy trong chương trước, một thuộc tính là có thể quyết định nếu bạn luôn có thể nói liệu thuộc tính đó có xảy ra với một số giá trị cụ thể hay không. Sử dụng hàm sau, bạn có thể thấy rằng Elem value xs là một thuộc tính có thể quyết định cho các giá trị cụ thể của value và xs, vì vậy Elem là một tiên đề có thể quyết định:

isElem : DecEq ty => (value : ty) -> (xs : Vect n ty) -> Dec (Elem value xs)

Loại isElem cho biết rằng miễn là bạn có thể quyết định sự bằng nhau của các giá trị trong một kiểu ty nào đó, bạn có thể quyết định xem một giá trị có kiểu ty có nằm trong một vector các kiểu ty hay không. Hãy nhớ rằng Dec có các bộ xây dựng sau:

Yes, which takes as its argument a proof that the predicate holds. In this case, that’s a value of type Elem value xs for whichever value and xs are passed as inputs to isElem.
No, which takes as its argument a proof that the predicate doesn’t hold. In this case, that’s a value of type Elem value xs -> Void.

`isElem được định nghĩa trong Data.Vect, nhưng thật hữu ích khi thấy cách tự viết nó. Danh sách dưới đây cho thấy điểm bắt đầu của chúng ta, xác định Elem bằng tay trong một tệp có tên ElemType.idr.`

Listing 9.4.
Defining `Elem` and `isElem` by hand (ElemType.idr)

data Elem : a -> Vect k a -> Type where Here : Elem x (x :: xs) There : (later : Elem x xs) -> Elem x (y :: xs) isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs)

Define, refine—Define the function by case splitting on the input vector xs:

isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = ?isElem_rhs_1 isElem value (x :: xs) = ?isElem_rhs_2

Refine— For ?isElem_rhs_1, value is clearly not in the empty vector, so you can return No. Remember that No takes as an argument a proof that you can’t construct the predicate. You can leave a hole for this argument for the moment:
```
isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No ?notInNil isElem value (x :: xs) = ?isElem_rhs_2
```
If you check the type of ?notInNil, you’ll see that to fill in this hole, you need to provide a proof that there can’t be an element of the empty vector:
```
 a : Type value : a constraint : DecEq a -------------------------------------- notInNil : Elem value [] -> Void
```
We’ll return to this hole shortly.
Refine— For ?isElem_rhs_2, if value and x are equal, you’ve found the value you’re looking for. You can use decEq, case-split on the result, and if the result is of the form Yes prf, return Yes with a hole for the proof that the value is the first in the vector:
```
isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No ?notInNil isElem value (x :: xs) = case decEq value x of Yes prf => Yes ?isElem_rhs_1 No notHere => ?isElem_rhs_3
```

Type, refine—You might like to fill the ?isElem_rhs_1 hole with Here, but if you check its type, you’ll see that you can’t quite use Here yet:

 a : Type value : a x : a prf : value = x k : Nat xs : Vect k a constraint : DecEq a -------------------------------------- isElem_rhs_1 : Elem value (x :: xs)

You can’t use Here because the type you’re looking for isn’t of the form Elem value (value :: xs). But prf tells you that value and x must be the same, so if you case-split on prf, you’ll get this:

isElem value (x :: xs) = case decEq value x of Yes Refl => Yes ?isElem_rhs_2 No notHere => ?isElem_rhs_3

The type of the newly created hole, ?isElem_rhs_2, is now in the form you need:

 a : Type value : a k : Nat xs : Vect k a constraint : DecEq a -------------------------------------- isElem_rhs_2 : Elem value (value :: xs)

You can fill in the ?isElem_rhs_2 using expression search in Atom:

isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No ?notInNil isElem value (x :: xs) = case decEq value x of Yes Refl => Yes Here No notHere => ?isElem_rhs_3

Refine— For ?isElem_rhs_3, value and x aren’t equal (you know this because decEq value x has returned a proof), so you can search recursively in xs:

isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No ?notInNil isElem value (x :: xs) = case decEq value x of Yes Refl => Yes Here No notHere => case isElem value xs of Yes prf => Yes ?isElem_rhs_1 No notThere => No ?isElem_rhs_2

Expression search will find the necessary proof for ?isElem_rhs_1. You can leave a hole for the No case for now:

isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No ?notInNil isElem value (x :: xs) = case decEq value x of Yes Refl => Yes Here No notHere => case isElem value xs of Yes prf => Yes (There prf) No notThere => No ?notInTail

At this stage, you can test the definition at the REPL. If a value is in a vector, you’ll see Yes and a proof:

*ElemType> isElem 3 [1,2,3,4,5] Yes (There (There Here)) : Dec (Elem 3 [1, 2, 3, 4, 5])

If not, you’ll see No, with a hole for the proof that the element is missing:

*ElemType> isElem 7 [1,2,3,4,5] No ?notInTail : Dec (Elem 7 [1, 2, 3, 4, 5])

To complete the definition, you’ll need to complete notInNil and notInTail.

Define, refine—You can complete ?notInNil by lifting it to a top-level function with Ctrl-Alt-L and then case splitting on its argument. Idris notices that neither input is possible:
```
notInNil : Elem value [] -> Void notInNil Here impossible notInNil (There _) impossible
```
Define— You can complete ?notInTail similarly, but you’ll need to work a bit harder to show that each case is impossible. Lifting to a top-level definition and then case splitting on the argument leads to the following:
```
notInTail : (notThere : Elem value xs -> Void) -> (notHere : (value = x) -> Void) -> Elem value (x :: xs) -> Void notInTail notThere notHere Here = ?notInTail_rhs_1 notInTail notThere notHere (There later) = ?notInTail_rhs_2
```
For each hole, remember to check its type and the type of its local variables, because these will often give a strong hint as to how to proceed.

Refine— For each case, you can use either notHere or notThere to produce the value of type Void that you need:

notInTail : (notThere : Elem value xs -> Void) -> (notHere : (value = x) -> Void) -> Elem value (x :: xs) -> Void notInTail notThere notHere Here = notHere Refl notInTail notThere notHere (There later) = notThere later

Đây là định nghĩa đã hoàn thành, để tham khảo.

Listing 9.5.
Complete definition of `isElem` (ElemType.idr)

notInNil : Elem value [] -> Void notInNil Here impossible notInNil (There _) impossible notInTail : (notThere : Elem value xs -> Void) -> (notHere : (value = x) -> Void) -> Elem value (x :: xs) -> Void notInTail notThere notHere Here = notHere Refl notInTail notThere notHere (There later) = notThere later isElem : DecEq a => (value : a) -> (xs : Vect n a) -> Dec (Elem value xs) isElem value [] = No notInNil isElem value (x :: xs) = case decEq value x of Yes Refl => Yes Here No notHere => case isElem value xs of Yes prf => Yes (There prf) No notThere => No (notInTail notThere notHere)

Để so sánh, danh sách 9.6 cho thấy cách bạn có thể định nghĩa một bài kiểm tra Boolean để kiểm tra thành viên trong vector. Ở đây, tôi đã sử dụng giao diện Eq, vì vậy chúng ta không có bất kỳ đảm bảo nào từ kiểu về cách hoạt động của bài kiểm tra bình đẳng. Tuy nhiên, elem theo cấu trúc tương tự như decElem.

Listing 9.6.
A Boolean test for whether a value is in a vector (ElemBool.idr)

elem : Eq ty => (value : ty) -> (xs : Vect n ty) -> Bool elem value [] = False elem value (x :: xs) = case value == x of False => elem value xs True => True

Cả hai định nghĩa có cấu trúc tương tự, nhưng cần nhiều công việc hơn trong isElem để chứng minh rằng các trường hợp không thể xảy ra thực sự là không thể. Đổi lại, không cần bất kỳ bài kiểm tra nào cho isElem, vì kiểu dữ liệu đủ chính xác để cho thấy rằng việc thực hiện phải đúng.

Exercises

Data.List includes a version of Elem for List that works similarly to Elem for Vect. How would you define it?

The following predicate states that a specific value is the last value in a List:

data Last : List a -> a -> Type where LastOne : Last [value] value LastCons : (prf : Last xs value) -> Last (x :: xs) value

So, for example, you can construct a proof of Last [1,2,3] 3:

last123 : Last [1,2,3] 3 last123 = LastCons (LastCons LastOne)

Write an isLast function that decides whether a value is the last element in a List. It should have the following type:

isLast : DecEq a => (xs : List a) -> (value : a) -> Dec (Last xs value)

You can test your answer at the REPL as follows:

*ex_9_1> isLast [1,2,3] 3 Yes (LastCons (LastCons LastOne)) : Dec (Last [1, 2, 3] 3)

9.2. Expressing program state in types: a guessing game

Trong thực tế, nhu cầu cho các tiên đề như Elem và các hàm như removeElem phát sinh một cách tự nhiên khi chúng ta viết các hàm thể hiện các đặc điểm của trạng thái hệ thống, chẳng hạn như độ dài của vector, trong các kiểu của chúng. Để kết thúc chương này, chúng ta sẽ xem xét một ví dụ nhỏ về nơi điều này xảy ra: sử dụng hệ thống kiểu để mã hóa các thuộc tính đơn giản của một trò chơi đoán từ, Hangman.

Trong trò chơi Treo, một người chơi cố gắng đoán một từ bằng cách đoán từng chữ cái một. Nếu họ đoán đúng tất cả các chữ cái trong từ, họ thắng. Ngược lại, họ được phép có một số lần đoán sai giới hạn, sau đó họ thua.

9.2.1.
Representing the game’s state

Danh sách 9.7 cho thấy cách chúng ta có thể biểu diễn trạng thái hiện tại của một trò chơi từ vựng dưới dạng một kiểu dữ liệu, WordState, trong Idris. Có hai phần quan trọng của trạng thái phản ánh các đặc điểm của trò chơi, và chúng được viết như các phần của kiểu.

The number of guesses the player has remaining
The number of letters the player still has to guess

Listing 9.7.
The game state (Hangman.idr)

Một trò chơi sẽ kết thúc nếu hoặc là số lần đoán còn lại bằng không (trong trường hợp này người chơi đã thua) hoặc số chữ cái còn lại bằng không (trong trường hợp này người chơi đã thắng). Danh sách 9.8 cho thấy cách chúng ta có thể đại diện điều này trong một kiểu dữ liệu. Chúng ta có thể chắc chắn rằng điều này chỉ bao gồm các trò chơi đã thắng hoặc thua, vì chúng ta đang bao gồm số lần đoán và số chữ cái còn lại như là các đối số cho WordState.

Listing 9.8.
Defining precisely when a game is in a finished state (Hangman.idr)

Loại dữ liệu WordState phụ thuộc lưu trữ dữ liệu cốt lõi cần thiết cho trò chơi. Bằng cách bao gồm các thành phần cốt lõi của quy tắc—số lần đoán và số chữ cái—như các tham số của WordState, chúng ta sẽ có thể thấy chính xác cách mà bất kỳ hàm nào sử dụng WordState thực hiện các quy tắc của trò chơi.

9.2.2.
A top-level game function

Chúng tôi sẽ áp dụng phương pháp từ trên xuống, xác định một chức năng cấp cao thực hiện một trò chơi hoàn chỉnh. Danh sách dưới đây cung cấp điểm khởi đầu.

Listing 9.9.
Top-level `game` function (Hangman.idr)

Loại trạng thái trò chơi cho biết rằng trò chơi có thể tiếp tục nếu còn ít nhất một lần đoán (S lượt đoán) và ít nhất một chữ cái vẫn chưa được đoán (S chữ cái). Nó trả về IO Finished, có nghĩa là nó thực hiện các hành động tương tác tạo ra dữ liệu trò chơi trong trạng thái Hoàn thành.

Để thực hiện trò chơi, bạn sẽ cần đọc một ký tự duy nhất từ người dùng (các đầu vào khác là không hợp lệ), kiểm tra xem ký tự mà người dùng nhập có trong từ mục tiêu trong trạng thái trò chơi hay không, cập nhật trạng thái trò chơi, và lặp lại nếu trò chơi chưa hoàn thành. Bạn có thể cập nhật trạng thái theo một trong các cách sau:

The letter is in the word, in which case you continue the game with the same number of guesses and one fewer letter.
The letter isn’t in the word, in which case you continue the game with one fewer guess and the same number of letters.

Số lượng dự đoán và các chữ cái đã sử dụng và còn lại được ghi rõ trong kiểu trạng thái của trò chơi. Do đó, bước tiếp theo là viết một hàm ghi lại những cập nhật trạng thái này trong kiểu của nó.

9.2.3.
A predicate for validating user input: ValidInput

Bạn có thể đọc đầu vào của người dùng bằng cách sử dụng hành động IO getLine:

getLine : IO String

Nhưng vì người dùng đang đoán một chữ cái, nên chỉ các đầu vào gồm chính xác một ký tự là hợp lệ. Để chính xác hơn, bạn có thể làm cho khái niệm về đầu vào hợp lệ trở nên rõ ràng hơn trong một tiên đề. Vì String là một kiểu nguyên thủy, nên khó khăn trong việc suy luận về các thành phần riêng biệt của nó trong một kiểu, vì vậy bạn có thể sử dụng một List Char để đại diện cho đầu vào trong tiên đề và chuyển đổi khi cần thiết.

data ValidInput : List Char -> Type where Letter : (c : Char) -> ValidInput [c]

Để kiểm tra xem một chuỗi có phải là đầu vào hợp lệ hay không, bạn có thể viết hàm sau, hàm này trả về bằng chứng rằng đầu vào là hợp lệ, hoặc bằng chứng rằng nó không bao giờ có thể hợp lệ, sử dụng Dec:

isValidString : (s : String) -> Dec (ValidInput (unpack s))

Bạn sẽ thấy định nghĩa của isValidString sớm thôi, trong phần 9.2.5. Như một bài tập, bạn có thể thử viết nó một mình, bắt đầu với hàm trợ giúp sau:

isValidInput : (cs : List Char) -> Dec (ValidInput cs)

Sau đó, thay vì sử dụng getLine, hãy viết một hàm readGuess trả về dự đoán của người dùng, cùng với một thể hiện của một predicate đảm bảo rằng dự đoán của người dùng là một đầu vào hợp lệ.

readGuess : IO (x ** ValidInput x)

`readGuess trả về một cặp phụ thuộc, trong đó phần tử đầu tiên là đầu vào được đọc từ console, và phần tử thứ hai là một điều kiện mà đầu vào phải thỏa mãn.`

Contracts on return values

Bằng cách trả về một giá trị kết hợp với một điều kiện về giá trị đó, kiểu của hàm readGuess đang thể hiện một hợp đồng mà giá trị trả về phải thỏa mãn.

Danh sách dưới đây cung cấp định nghĩa của readGuess.

Listing 9.10.
Read a guess from the console, which is guaranteed to be valid (Hangman.idr)

Bằng cách sử dụng readGuess, bạn có thể chắc chắn rằng bất kỳ chuỗi hợp lệ nào được đọc từ console đều đảm bảo có đúng một ký tự.

9.2.4.
Processing a guess

Việc xử lý một dự đoán sẽ trả về trạng thái trò chơi với một loại nếu dự đoán là đúng, và một loại khác nếu dự đoán sai. Bạn có thể sử dụng kiểu tổng quát Either để đại diện cho điều này. Hãy nhớ rằng Either là một kiểu tổng quát được định nghĩa trong Prelude, mang một giá trị của hai kiểu khả thi.

data Either a b = Left a | Right b

`Either thường được sử dụng để đại diện cho kết quả của một phép toán có thể thất bại, mang thông tin về lỗi nếu nó thất bại. Theo quy ước, chúng ta sử dụng Left cho trường hợp lỗi và Right cho trường hợp thành công. Bạn có thể nghĩ rằng một đoán sai là trường hợp lỗi, vì vậy danh sách tiếp theo hiển thị kiểu mà bạn sẽ sử dụng cho một hàm xử lý một lần đoán.`

Sure! Please provide the text you would like me to translate into Vietnamese.
“Right” also being a synonym of “correct.”

Listing 9.11.
Type of a function that processes a user’s guess (Hangman.idr)

Loại này cho biết rằng, với một chữ cái và một trạng thái trò chơi đầu vào, nó sẽ tạo ra một trạng thái trò chơi mới, nơi số lần đoán còn lại đã giảm (đoán sai), hoặc nơi số chữ cái còn lại đã giảm (đoán đúng).

Types as abstract state

Một giá trị của kiểu WordState đoán chữ giữ thông tin cụ thể về trạng thái hệ thống, bao gồm từ chính xác cần được đoán và chính xác những chữ cái nào vẫn còn thiếu. Kiểu dữ liệu này tự nó thể hiện thông tin trừu tượng về trạng thái trò chơi (số lần đoán còn lại và số chữ cái còn thiếu), cho phép bạn diễn đạt các quy tắc trong các kiểu hàm như processGuess.

Bạn có thể triển khai processGuess như sau:

Define— You need to inspect the input game state, so you can case-split on the input state:

processGuess : (letter : Char) -> WordState (S guesses) (S letters) -> Either (WordState guesses (S letters)) (WordState (S guesses) letters) processGuess letter (MkWordState word missing) = ?guess_rhs_1

Define— If the guessed letter is correct, it’ll be in the missing vector, and you’ll need to remove it. You can use isElem to find whether it’s there and define the function by case splitting on the result of isElem:
```
processGuess letter (MkWordState word missing) = case isElem letter missing of Yes prf => ?guess_rhs_2 No contra => ?guess_rhs_3
```
Refine— If the letter is in the vector of missing letters, you’ll return a new state with one fewer letters to guess. Otherwise, you’ll return a new state with one fewer guess available:
```
processGuess letter (MkWordState word missing) = case isElem letter missing of Yes prf => Right (MkWordState word ?nextVect) No contra => Left (MkWordState word missing)
```
You have a hole, ?nextVect, for the updated vector of missing letters.

Type, refine—The type of ?nextVect shows that you need to remove an element from the vector:

 word : String letter : Char letters : Nat missing : Vect (S letters) Char prf : Elem letter missing guesses : Nat -------------------------------------- nextVect : Vect letters Char

You can complete the definition by using removeElem to remove letter from missing, and Idris will find the necessary proof, prf, as an auto implicit. This completes the definition:

processGuess : (letter : Char) -> WordState (S guesses) (S letters) -> Either (WordState guesses (S letters)) (WordState (S guesses) letters) processGuess letter (MkWordState word missing) = case isElem letter missing of Yes prf => Right (MkWordState word (removeElem letter missing)) No contra => Left (MkWordState word missing)

Explicit assumptions

Trong trạng thái trò chơi, bạn giả định rằng số lượng chữ cái còn lại để đoán là giống như độ dài của vector các chữ cái còn thiếu. Bằng cách đưa điều này vào loại WordState và loại processGuess, bạn có thể chắc chắn rằng nếu bạn bao giờ vi phạm giả định này, chương trình của bạn sẽ không còn biên dịch được nữa.

Bạn có thể hoàn thành định nghĩa của trò chơi bằng cách sử dụng processGuess để cập nhật trạng thái trò chơi khi cần thiết.

9.2.5.
Deciding input validity: checking ValidInput

Trước khi hoàn thành việc triển khai trò chơi, bạn cần hoàn thành việc triển khai hàm isValidString, hàm này quyết định xem một chuỗi do người dùng nhập vào có phải là đầu vào hợp lệ hay không.

Listing 9.12.
Showing that an input string must be either a valid or invalid input (Hangman.idr)

Bạn có thể kiểm tra định nghĩa này tại REPL bằng cách sử dụng >>= để lấy kết quả của read-Guess, so khớp với thành phần đầu tiên của cặp phụ thuộc, và truyền nó tới printLn:

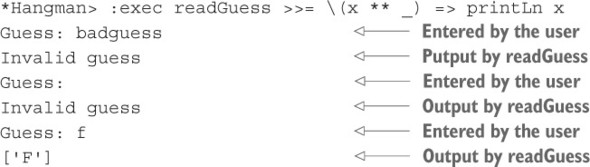
Bây giờ bạn đã có khả năng đọc đầu vào được đảm bảo là ở dạng hợp lệ và khả năng xử lý các phỏng đoán để cập nhật trạng thái trò chơi, bạn có thể hoàn thành việc triển khai trò chơi ở cấp cao nhất.

9.2.6.
Completing the top-level game implementation

Danh sách tiếp theo cho thấy một cách có thể (nếu cơ bản) để hoàn thành việc triển khai trò chơi. Nó sử dụng processGuess để kiểm tra đầu vào của người dùng và báo cáo liệu một lần đoán là chính xác hay sai cho đến khi người chơi thắng hoặc thua.

Listing 9.13.
Top-level `game` function (Hangman.idr)

Bằng cách bao gồm số lượt đoán và số chữ cái còn lại trong kiểu, bạn đã hầu như viết ra một quy tắc quan trọng của trò chơi trong kiểu của hàm đoán. Kết quả là, những loại lỗi nhất định trong việc thực hiện sẽ không xảy ra. Ví dụ, miễn là bạn luôn sử dụng hàm đoán để cập nhật trạng thái trò chơi, bạn sẽ tránh được những vấn đề tiềm ẩn sau đây:

It’s impossible to test the wrong variable (guesses or letters) before continuing the game.^[2] Doing so would cause a type error.

Sure, please provide the text you would like to have translated into Vietnamese.
I really did make this mistake when writing this example!
It’s impossible to continue a completed game, because there must be at least one guess remaining and at least one letter to guess.
It’s impossible to finish a game prematurely, when there are both missing letters and guesses still available.

Danh sách dưới đây cho thấy một triển khai có thể có của hàm main để thiết lập một trò chơi với một từ mục tiêu, "Test", yêu cầu người chơi đoán các chữ cái 'T', 'E', và 'S'.

Listing 9.14.
A `main` program to set up a game (Hangman.idr)

9.3. Summary

You can write types that express assumptions about how values relate.
The Elem dependent type is a predicate that expresses that a value must be contained in a vector.
By passing a predicate as an argument to a function, you can express a contract that the inputs to the function must follow.
You can write a function to show that a predicate is decidable, using Dec.
Idris will attempt to find values for arguments marked auto by expression search.
You can capture properties of a system’s state (such as the rules of a game) in a type.
Predicates can describe the validity of user input and ensure that the user input is validated when necessary.

Chapter 10.
Views: extending pattern matching

Chương này đề cập đến

Defining views, which describe alternative forms of pattern matching
Introducing the with construct for working with views
Describing efficient traversals of data structures
Hiding the representation of data behind views

Trong phát triển dựa trên loại, phương pháp của chúng tôi trong việc triển khai các hàm là viết một loại, định nghĩa cấu trúc của hàm bằng cách chia trường hợp trên các đối số của nó, và hoàn thiện hàm bằng cách lấp đầy các khoảng trống. Trong bước định nghĩa, chúng tôi đặc biệt sử dụng cấu trúc của các loại đầu vào để dẫn dắt cấu trúc của toàn bộ hàm.

Như bạn đã học trong chương 3, khi bạn chia nhánh dựa trên một biến, các mẫu phát sinh từ loại của biến đó. Cụ thể, các mẫu phát sinh từ các nhà xây dựng dữ liệu có thể được sử dụng để tạo ra các giá trị của loại đó. Ví dụ, nếu bạn chia nhánh dựa trên một biến items có loại List elem, các mẫu sau sẽ phát sinh:

[]—Represents the empty list
(x :: xs)—Represents a non-empty list with x as the first element and xs as the list of the remaining elements

Do đó, khớp mẫu sẽ phân tách các biến thành các thành phần của chúng. Thường thì, bạn sẽ muốn phân tách các biến theo những cách khác nhau. Ví dụ, bạn có thể muốn phân tách một danh sách đầu vào thành một trong các dạng sau:

A list of all but the last element, and then the last element
Two sublists—the first half and the second half of the input

Trong chương này, bạn sẽ thấy cách mở rộng các hình thức mẫu mà bạn có thể sử dụng bằng cách định nghĩa các kiểu dữ liệu thông tin, được gọi là các view. Các view là các kiểu phụ thuộc có tham số bởi dữ liệu mà bạn muốn khớp, và chúng mang lại cho bạn những cách mới để quan sát dữ liệu đó. Ví dụ, các view có thể làm những điều sau:

Describe new forms of patterns, such as allowing you to match against the last element of a list rather than the first
Define alternative ways of traversing data structures, such as traversing a list in reverse, or by repeatedly splitting the list into halves
Hide complex data representations behind an abstract interface while still supporting pattern-matching on that data

Chúng ta sẽ bắt đầu bằng cách xem xét cách sử dụng views để định nghĩa các phương pháp thay thế cho việc khớp trên danh sách, chẳng hạn như xử lý phần tử cuối cùng trước. Sau đó, chúng ta sẽ xem xét cách định nghĩa các phép duyệt danh sách hiệu quả và đảm bảo rằng chúng kết thúc, và chúng ta sẽ xem một số phép duyệt được cung cấp bởi thư viện Idris. Cuối cùng, chúng ta sẽ sử dụng views để hỗ trợ trừu tượng dữ liệu bằng cách ẩn cấu trúc dữ liệu trong một module riêng biệt và thực hiện việc khớp và duyệt dữ liệu bằng cách sử dụng một view.

10.1. Defining and using views

Khi bạn viết một mẫu (x :: xs) để khớp với một danh sách, x sẽ nhận giá trị của phần tử đầu tiên trong danh sách và xs sẽ nhận giá trị của đuôi danh sách. Bạn đã thấy hàm sau đây trong chương 3 để mô tả cách một danh sách được cấu tạo, được minh họa lại trong hình 10.1:

describeList : List Int -> String describeList [] = "Empty" describeList (x :: xs) = "Non-empty, tail = " ++ show xs

Figure 10.1.
Matching the pattern `(x :: xs)` for inputs `[1]` and `[2,3,4,5]`

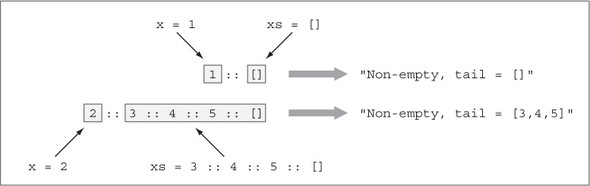
Kết quả là, việc so sánh danh sách sử dụng mẫu (x :: xs) có nghĩa là bạn sẽ luôn duyệt danh sách từ đầu đến cuối, xử lý x trước, rồi sau đó xử lý phần còn lại, xs. Nhưng đôi khi việc duyệt danh sách theo chiều ngược lại, xử lý phần tử cuối cùng trước, lại tiện lợi hơn.

Bạn có thể thêm một phần tử đơn vào cuối danh sách bằng cách sử dụng toán tử ++:

Idris> [2,3,4] ++ [5] [2, 3, 4, 5] : List Integer

Thật tuyệt nếu có thể khớp các mẫu có dạng (xs ++ [x]), trong đó x nhận giá trị của phần tử cuối cùng của danh sách và xs nhận giá trị của đoạn đầu tiên của danh sách. Điều này có nghĩa là bạn có thể muốn viết một hàm có dạng như sau, như đã minh họa trong hình 10.2:

Figure 10.2.
Matching the pattern `(xs ++ [x])` for inputs `[1]` and `[2,3,4,5]`

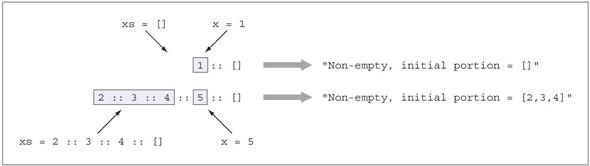
Thật không may, nếu bạn cố gắng triển khai describeListEnd, nó sẽ bị lỗi với thông báo sau:

DLFail.idr:3:19: When checking left hand side of describeListEnd: Can't match on describeListEnd (xs ++ [x])

Vấn đề là bạn đang cố gắng khớp mẫu dựa trên kết quả của một hàm, ++, và nhìn chung không có cách nào để Idris tự động suy luận các đầu vào của một hàm tùy ý từ đầu ra của nó. Tuy nhiên, bạn có thể mở rộng các hình thức của các mẫu mà bạn có thể sử dụng bằng cách định nghĩa các kiểu dữ liệu thông tin gọi là views. Ở phần này, bạn sẽ thấy cách định nghĩa views, và tôi sẽ giới thiệu cấu trúc with, cung cấp một cách ghi chú ngắn gọn để định nghĩa các hàm sử dụng views.

10.1.1.
Matching the last item in a list

Bạn không thể viết describeListEnd trực tiếp vì bạn không thể khớp một mẫu theo dạng (xs ++ [x]) một cách trực tiếp. Tuy nhiên, bạn có thể tận dụng việc khớp mẫu phụ thuộc để suy luận rằng một đầu vào cụ thể phải có dạng (xs ++ [x]). Bạn đã thấy khớp mẫu phụ thuộc trong chương 6, nơi việc kiểm tra giá trị của một đối số (tức là phân tách trường hợp trên đối số đó) có thể cho bạn biết về dạng của một đối số khác. Bằng cách sử dụng khớp mẫu phụ thuộc, bạn có thể mô tả các mẫu thay thế cho danh sách.

Danh sách dưới đây cho thấy loại phụ thuộc ListLast, mô tả hai dạng có thể của một danh sách. Một danh sách có thể là rỗng, [], hoặc được xây dựng từ phần đầu của một danh sách và phần tử cuối cùng của nó.

Listing 10.1.
The `ListLast` dependent type, which gives alternative patterns for a list (DescribeList.idr)

Sử dụng ListLast, cùng với việc khớp mẫu phụ thuộc, bạn có thể định nghĩa describe-ListEnd. Bạn sẽ bắt đầu bằng cách định nghĩa một hàm trợ giúp nhận một danh sách đầu vào, input, và một tham số bổ sung, form, cho biết liệu danh sách đó có rỗng hay không.

Type— Begin with the type. You’ll use ListLast to describe the possible forms that input can take:

describeHelper : (input : List Int) -> (form : ListLast input) -> String describeHelper input form = ?describeHelper_rhs

Define— You want to describe input, so you’ll need to inspect its form somehow. Previously, when defining a function to inspect the form of an input, you’ve case-split on that input. Here, the intention of the form argument is to tell you more about input, so case-split on that instead:
```
describeHelper : (input : List Int) -> (form : ListLast input) -> String describeHelper [] Empty = ?describeHelper_rhs_1 describeHelper (xs ++ [x]) (NonEmpty xs x) = ?describeHelper_rhs_2
```
Notice that the case split on form has told you more about the form of input. In particular, the type of NonEmpty means that if form has the value NonEmpty xs x, then input must have the value (xs ++ [x]).

Refine— Complete the definition by describing the patterns as in our initial attempt at describeListEnd:

describeHelper : (input : List Int) -> ListLast input -> String describeHelper [] Empty = "Empty" describeHelper (xs ++ [x]) (NonEmpty xs x) = "Non-empty, initial portion = " ++ show xs

ListLast là một cách xem các danh sách vì nó cung cấp một phương thức thay thế để xem dữ liệu. Tuy nhiên, nó là một kiểu dữ liệu thông thường, và để sử dụng ListLast trong thực tế, bạn sẽ cần phải có khả năng chuyển đổi một danh sách đầu vào, xs, thành một giá trị có kiểu ListLast xs.

10.1.2.
Building views: covering functions

Danh sách tiếp theo hiển thị listLast, chuyển đổi một danh sách đầu vào, xs, thành một thể hiện của một cái nhìn, ListLast xs, cho phép truy cập vào phần tử cuối cùng của xs.

Listing 10.2.
Describing a `List` in the form `ListLast` (DescribeList.idr)

`listLast là hàm bao phủ của view ListLast. Một hàm bao phủ của một view mô tả cách chuyển đổi giá trị (trong trường hợp này là danh sách đầu vào) thành một view của giá trị đó (trong trường hợp này, một danh sách xs và một giá trị x, trong đó xs ++ [x] = đầu vào).`

Naming convention for covering functions

Theo quy ước, các hàm bao phủ được đặt tên giống như loại view, nhưng với chữ cái đầu tiên viết thường.

Bây giờ bạn có thể mô tả bất kỳ Danh sách nào theo dạng ListLast, bạn có thể hoàn thiện định nghĩa của describeListEnd:

describeHelper : (input : List Int) -> ListLast input -> String describeHelper [] Empty = "Empty" describeHelper (xs ++ [x]) (NonEmpty xs x) = "Non-empty, initial portion = " ++ show xs describeListEnd : List Int -> String describeListEnd xs = describeHelper xs (listLast xs)

Điều này hoạt động như chúng tôi đã dự định trong nỗ lực ban đầu về describeListEnd, với các mẫu gốc trong describeHelper. Nếu bạn đang sử dụng một khái niệm khác về việc khớp mẫu so với mặc định, bạn nên kỳ vọng sẽ phải sử dụng một số ký hiệu bổ sung để giải thích cách khớp mẫu (xs ++ [x]), nhưng định nghĩa tổng thể vẫn cảm thấy khá dài dòng.

Bởi vì việc khớp mẫu phụ thuộc theo cách này là một phương thức lập trình phổ biến trong Idris, có một cấu trúc để diễn đạt việc khớp mẫu mở rộng một cách ngắn gọn hơn: cấu trúc with.

10.1.3.
with blocks: syntax for extended pattern matching

Sử dụng các view để tạo ra các mẫu thông tin như (xs ++ [x]) có thể giúp tăng cường khả năng đọc hiểu của các hàm và tăng cường sự tự tin vào độ chính xác của chúng vì các kiểu dữ liệu cho bạn biết chính xác đầu vào cần phải có hình thức gì. Nhưng những hàm này có thể hơi dài dòng hơn bởi vì bạn cần tạo một hàm trợ giúp bổ sung (như describeHelper) để thực hiện việc khớp mẫu cần thiết. Cấu trúc with cung cấp một cách viết cho việc sử dụng các view một cách ngắn gọn hơn.

Bằng cách sử dụng các khối with, bạn có thể thêm các đối số bổ sung vào bên trái của một định nghĩa, giúp bạn có nhiều đối số hơn để phân chia trường hợp. Cách dễ nhất để thấy cách điều này hoạt động là qua ví dụ, vì vậy hãy cùng xem xét cách bạn có thể sử dụng một khối with để định nghĩa describeListEnd:

Type— Begin with a top-level type that takes a List Int and returns a String:

describeListEnd : List Int -> String describeListEnd input = ?describeListEnd_rhs

Define— Press Ctrl-Alt-W with the cursor on the line with the hole ?describe-ListEnd_rhs. This adds a new pattern clause as follows (it won’t yet type-check):
```
describeListEnd : List Int -> String describeListEnd input with (_) describeListEnd input | with_pat = ?describeListEnd_rhs
```
Define— The with syntax adds a new argument to the left side of the definition. The brackets after with give the value of that argument, and the (indented) clause beneath contains the extra argument, after a vertical bar. Here, you’ll match on the result of listLast input, so replace the _ with listLast input:
```
describeListEnd : List Int -> String describeListEnd input with (listLast input) describeListEnd input | with_pat = ?describeListEnd_rhs
```
Type— If you check the type of ?describeListEnd_rhs, you can see more detail about how with works, looking specifically at the type of with_pat:
```
 input : List Int with_pat : ListLast input -------------------------------------- describeListEnd_rhs : String
```
The value of with_pat is the result of listLast input. Figure 10.3 shows the components of the syntax for the with construct. Note that the scope of the with block is managed by indentation.
Figure 10.3.
Syntax for the with construct
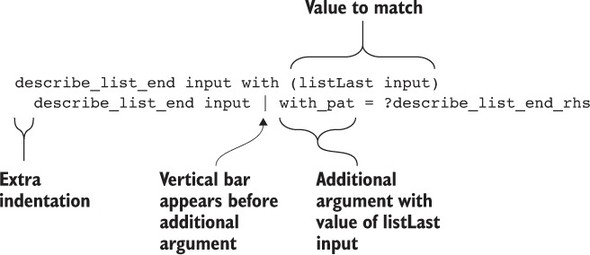
Define—
Notice that the types of input and with_pat are exactly the same as the types of the inputs to describeHelper earlier. And as in the definition of describeHelper, if you case-split on with_pat, you’ll learn more about the form of input:
```
describeListEnd : List Int -> String describeListEnd input with (listLast input) describeListEnd [] | Empty = ?describeListEnd_rhs_1 describeListEnd (xs ++ [x]) | (NonEmpty xs x) = ?describeListEnd_rhs_2
```

Refine— Complete the definition as before, with the description of the patterns:

describeListEnd : List Int -> String describeListEnd input with (listLast input) describeListEnd [] | Empty = "Empty" describeListEnd (xs ++ [x]) | (NonEmpty xs x) = "Non-empty, initial portion = " ++ show xs

Về cơ bản, cấu trúc with đã cho phép bạn sử dụng một mẫu trung gian để khớp với kết quả đầu vào của listLast, mà không cần định nghĩa một hàm riêng biệt như describeHelper. Ngược lại, việc khớp với kết quả đầu vào của listLast mang lại cho bạn các mẫu thông tin rõ ràng hơn cho đầu vào.

The difference between with and case

Mục đích của cấu trúc with tương tự như một khối case ở chỗ nó cho phép khớp với các kết quả trung gian. Tuy nhiên, có một sự khác biệt quan trọng: with giới thiệu một mẫu mới để khớp ở phía bên trái của một định nghĩa. Kết quả là, bạn có thể sử dụng khớp mẫu phụ thuộc trực tiếp. Trong describeListEnd, ví dụ, việc khớp với kết quả của listLast input đã cho bạn biết về hình thức mà input phải có.

Bạn không thể sử dụng bất kỳ biểu thức nào trong một mẫu vì về cơ bản, không thể quyết định những gì mà đầu vào của một hàm phải là, chỉ dựa trên kết quả của nó. Idris do đó chỉ cho phép các mẫu khi nó có thể suy luận những đầu vào đó, điều này xảy ra trong các trường hợp sau:

The pattern consists of a data constructor applied to some arguments. The arguments must also be valid patterns.
The value of the pattern is forced by some other valid pattern. In the case of describeListEnd, the value of the pattern (xs ++ [x]) is forced by the valid pattern NonEmpty xs x.

10.1.4.
Example: reversing a list using a view

Khi bạn có khả năng nhận dạng mẫu theo nhiều cách khác nhau bằng cách sử dụng các view, bạn có thể di chuyển qua các cấu trúc dữ liệu theo những cách mới. Thay vì luôn luôn duyệt một danh sách từ trái sang phải, ví dụ, bạn có thể sử dụng listLast để duyệt một danh sách từ phải sang trái, kiểm tra phần tử cuối cùng trước.

Bạn có thể đảo ngược một danh sách theo cách này:

To reverse an empty list [], return [].
To reverse a list in the form xs ++ [x], reverse xs and then add x to the front of the list.

Bạn có thể triển khai thuật toán này khá trực tiếp bằng cách sử dụng chế độ xem ListLast:

Type— Call the function myReverse because there’s already a reverse function in the Prelude:
```
myReverse : List a -> List a myReverse input = ?myReverse_rhs
```
Define— You’ll define the function by inspecting the last element of the input first, so you can use listLast to match on a value of type ListLast input. Press Ctrl-Alt-W to insert a with block, and add listLast input as the value to inspect:
```
myReverse : List a -> List a myReverse input with (listLast input) myReverse input | with_pat = ?myReverse_rhs
```

Define— Next, case-split on with_pat to give the relevant patterns for input:

myReverse : List a -> List a myReverse input with (listLast input) myReverse [] | Empty = ?myReverse_rhs_1 myReverse (xs ++ [x]) | (NonEmpty xs x) = ?myReverse_rhs_2

Refine— Finally, you can complete the definition as follows:

myReverse : List a -> List a myReverse input with (listLast input) myReverse [] | Empty = [] myReverse (xs ++ [x]) | (NonEmpty xs x) = x :: myReverse xs

Đây là một triển khai khá trực tiếp của thuật toán, duyệt danh sách theo chiều ngược lại và xây dựng một danh sách mới bằng cách thêm mục cuối cùng của đầu vào thành mục đầu tiên của kết quả. Tuy nhiên, có hai vấn đề:

The definition is inefficient because it constructs ListLast input on every recursive call, and constructing ListLast input requires traversing input.

Idris can’t decide whether the definition is total or not:

*Reverse> :total myReverse Main.myReverse is possibly not total due to: possibly not total due to recursive path: with block in Main.myReverse, with block in Main.myReverse

See the sidebar for a brief discussion on totality checking in Idris.

Vấn đề đầu tiên là quan trọng để giải quyết, vì có thể viết myReverse trong thời gian tuyến tính, chỉ đi qua danh sách đầu vào một lần. Vấn đề thứ hai quan trọng từ góc độ phát triển dựa trên loại: như tôi đã thảo luận trong chương 1, nếu Idris có thể xác định rằng một hàm là tổng quát, bạn có một đảm bảo mạnh mẽ rằng kiểu dữ liệu mô tả chính xác những gì hàm sẽ làm. Nếu không, bạn chỉ có một đảm bảo rằng hàm sẽ tạo ra một giá trị của kiểu dữ liệu đã cho nếu nó kết thúc mà không gặp sự cố. Hơn nữa, nếu Idris không thể xác định rằng một hàm là tổng quát, nó cũng không thể xác định rằng bất kỳ hàm nào gọi hàm đó là tổng quát.

Chúng ta sẽ xem xét cách giải quyết từng vấn đề này, với chỉ một số thay đổi nhỏ đối với myReverse, trong phần 10.2.

Totality checking

Idris cố gắng xác định xem một hàm có luôn luôn kết thúc hay không bằng cách kiểm tra hai điều sau:

There must be patterns for all possible well-typed inputs.
When there is a recursive call (or a sequence of mutually recursive calls), there must be a decreasing argument that converges toward a base case.

Để xác định các đối số nào là giảm, Idris xem xét các mẫu cho các đầu vào trong một định nghĩa. Nếu một mẫu có dạng của một khởi tạo dữ liệu, Idris coi các đối số trong mẫu đó là nhỏ hơn đầu vào. Trong myReverse, ví dụ, Idris không coi xs là nhỏ hơn (xs ++ [x]), vì (xs ++ [x]) không có dạng của một khởi tạo dữ liệu.

Hạn chế này giữ cho khái niệm lập luận giảm dần đơn giản để Idris kiểm tra. Nói chung, Idris không thể xác định liệu các đầu vào của một hàm có luôn nhỏ hơn kết quả hay không.

Như bạn sẽ thấy trong phần 10.2, bạn có thể vượt qua hạn chế này bằng cách định nghĩa các view đệ quy.

10.1.5.
Example: merge sort

Các view cho phép bạn mô tả việc khớp trên các cấu trúc dữ liệu theo bất kỳ cách nào bạn muốn, với bất kỳ số lượng mẫu nào bạn thích, miễn là bạn có thể thực hiện một hàm phủ cho view đó. Là một ví dụ thứ hai về view, chúng ta sẽ triển khai thuật toán sắp xếp hòa trộn trên danh sách.

Sắp xếp hợp nhất, ở mức độ cao, hoạt động như sau:

If the input is an empty list, return an empty list.
If the input has one element, it’s already sorted, so return the input.
In all other cases, split the list into two halves (differing in size by at most one), recursively sort those halves, and then merge the two sorted halves into a sorted list (see figure 10.4).

Figure 10.4.
Sorting a list using merge sort: split the list into two halves, sort the halves, and then merge the sorted halves back together

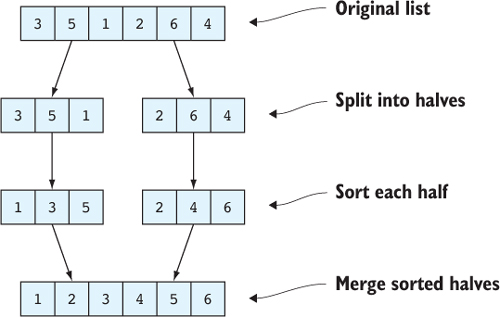
Nếu bạn có hai danh sách đã sắp xếp, bạn có thể hợp nhất chúng với nhau bằng cách sử dụng hàm hợp nhất được định nghĩa trong Prelude:

Idris> :doc merge Prelude.List.merge : Ord a => List a -> List a -> List a Merge two sorted lists using the default ordering for the type of their elements.

Lưu ý rằng nó có một kiểu tổng quát và yêu cầu phải triển khai giao diện Ord cho loại phần tử của danh sách.

Giả sử rằng hai danh sách đầu vào đã được sắp xếp, việc hợp nhất sẽ tạo ra một danh sách đã được sắp xếp của các phần tử trong các danh sách đầu vào. Ví dụ, các danh sách trong hình 10.4 sẽ được hợp nhất như sau:

Idris> merge [1,3,5] [2,4,6] [1, 2, 3, 4, 5, 6] : List Integer

Danh sách 10.3 cho thấy cách bạn có thể lý tưởng muốn viết một hàm mergeSort để sắp xếp một danh sách bằng thuật toán sắp xếp hợp nhất. Thật không may, như hiện tại, điều này sẽ không hoạt động vì (lefts ++ rights) không phải là một mẫu hợp lệ.

Listing 10.3.
Initial attempt at `mergeSort` with an invalid pattern (MergeSort.idr)

Xét một danh sách đầu vào so khớp với một mẫu, (lefts ++ rights), Idris thường không thể suy ra lefts và rights phải như thế nào; thực tế, có thể có vài khả năng hợp lý nếu danh sách đầu vào có một hoặc nhiều phần tử. Dưới đây là một vài ví dụ:

[1] could match against (lefts ++ rights) with lefts as [1] and rights as [], or lefts as [] and rights as [1].
[1,2,3] could match against (lefts ++ rights) with lefts as [1] and rights as [2,3], or lefts as [1,2] and rights as [3], among many other possibilities.

Để phù hợp với các mẫu mà chúng tôi muốn, như được trình bày trong danh sách 10.3, bạn sẽ cần tạo một chế độ xem của danh sách, SplitList, để cung cấp các mẫu mà bạn muốn. Danh sách dưới đây cho thấy định nghĩa của SplitList và cung cấp kiểu cho hàm bao phủ của nó, splitList.

Listing 10.4.
A view of lists that gives patterns for empty lists, singleton lists, and concatenating lists (MergeSort.idr)

data SplitList : List a -> Type where SplitNil : SplitList [] SplitOne : SplitList [x] SplitPair : (lefts : List a) -> (rights : List a) -> SplitList (lefts ++ rights) splitList : (input : List a) -> SplitList input

Tôi sẽ đưa ra định nghĩa về hàm bao phủ, splitList, sớm thôi. Hiện tại, hãy lưu ý rằng miễn là việc triển khai splitList là tổng quát, bạn có thể chắc chắn từ kiểu của nó rằng nó đưa ra các mẫu hợp lệ cho danh sách rỗng, danh sách đơn lẻ hoặc sự nối của hai danh sách. Tuy nhiên, bạn không có bất kỳ đảm bảo nào trong kiểu về cách một danh sách được tách thành các cặp; trong trường hợp này, bạn cần phụ thuộc vào việc triển khai để đảm bảo rằng các phần trái và phải khác nhau về kích thước không quá một.

Precision of SplitPair

Về nguyên tắc, bạn có thể làm cho kiểu SplitPair chính xác hơn và mang theo một chứng minh rằng phần bên trái và bên phải khác nhau về kích thước tối đa là một. Thực tế, module thư viện Idris Data.List.Views xuất khẩu một cái nhìn như vậy, gọi là SplitBalanced.

Bạn có thể triển khai mergeSort sử dụng view SplitList như sau:

Type— Begin with the type and a skeleton definition:

mergeSort : Ord a => List a -> List a mergeSort input = ?mergeSort_rhs

Define— To get the patterns you want, you’ll need to use the SplitList view you’ve just created. Add a with block and use the splitList covering function:
```
mergeSort : Ord a => List a -> List a mergeSort input with (splitList input) mergeSort input | with_pat = ?mergeSort_rhs
```

Define— If you case-split on with_pat, you’ll get appropriate patterns for input arising from the types of the constructors to SplitList:

mergeSort : Ord a => List a -> List a mergeSort input with (splitList input) mergeSort [] | SplitNil = ?mergeSort_rhs_1 mergeSort [x] | SplitOne = ?mergeSort_rhs_2 mergeSort (lefts ++ rights) | (SplitPair lefts rights) = ?mergeSort_rhs_3

Refine— You can complete the definition by filling in the right sides for each pattern, directly following the high-level description of the merge sort algorithm I gave at the start of this section:

mergeSort : Ord a => List a -> List a mergeSort input with (splitList input) mergeSort [] | SplitNil = [] mergeSort [x] | SplitOne = [x] mergeSort (lefts ++ rights) | (SplitPair lefts rights) = merge (mergeSort lefts) (mergeSort rights)

Trước khi bạn có thể kiểm tra mergeSort, bạn sẽ cần triển khai hàm bao phủ splitList. Danh sách tiếp theo cung cấp định nghĩa của splitList mà trả về mô tả của mẫu danh sách rỗng, mẫu danh sách đơn lẻ, hoặc một mẫu bao gồm sự kết hợp của hai danh sách, trong đó hai danh sách đó khác nhau về độ dài không quá một.

Listing 10.5.
Defining a covering function for `SplitList` (MergeSort.idr)

Bạn xây dựng hai danh sách (khoảng) có kích thước bằng nhau bằng cách sử dụng một tham chiếu thứ hai đến danh sách đầu vào như một bộ đếm trong một hàm trợ giúp, splitListHelp, như sau:

On each recursive call, the counter steps through two elements of the list. The pattern (_ :: _ :: counter) matches any list with at least two elements, where counter is a list containing all but the first two elements.
When the counter reaches the end of the list (that is, fewer than two elements remain), you must have traversed half of the input.

Bạn có thể thử splitList và mergeSort tại REPL:

*MergeSort> splitList [1] SplitOne : SplitList [1] *MergeSort> splitList [1,2,3,4,5] SplitPair [1, 2] [3, 4, 5] : SplitList [1, 2, 3, 4, 5] *MergeSort> mergeSort [3,2,1] [1, 2, 3] : List Integer *MergeSort> mergeSort [5,1,4,3,2,6,8,7,9] [1, 2, 3, 4, 5, 6, 7, 8, 9] : List Integer

Bằng cách định nghĩa một kiểu xem cho các trường hợp có thể xảy ra của danh sách đầu vào liên quan đến cách nó có thể được chia thành hai, bạn có thể viết một định nghĩa của mergeSort trực tiếp thực hiện mô tả cấp cao về thuật toán.

Giống như myReverse, tuy nhiên, Idris không thể xác định xem mergeSort có toàn bộ hay không:

*MergeSort> :total mergeSort Main.mergeSort is possibly not total due to: possibly not total due to recursive path: with block in Main.mergeSort, with block in Main.mergeSort

Một lần nữa, vấn đề là Idris không thể nhận ra rằng các lời gọi đệ quy được đảm bảo sẽ được thực hiện trên các danh sách nhỏ hơn so với đầu vào ban đầu. Ở phần tiếp theo, bạn sẽ thấy cách giải quyết vấn đề này bằng cách định nghĩa các quan điểm đệ quy mô tả cấu trúc đệ quy của một hàm, cũng như các mẫu xác định một hàm.

Exercises

The TakeN view allows traversal of a list several elements at a time:

data TakeN : List a -> Type where Fewer : TakeN xs Exact : (n_xs : List a) -> TakeN (n_xs ++ rest) takeN : (n : Nat) -> (xs : List a) -> TakeN xs

The Fewer constructor covers the case where there are fewer than n elements. Define the covering function takeN. To check that your definition works, you should be able to run the following function, which groups lists into sublists with n elements each:

groupByN : (n : Nat) -> (xs : List a) -> List (List a) groupByN n xs with (takeN n xs) groupByN n xs | Fewer = [xs] groupByN n (n_xs ++ rest) | (Exact n_xs) = n_xs :: groupByN n rest

Here’s an example:

*ex_10_1> groupByN 3 [1..10] [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10]] : List (List Integer)

Use TakeN to define a function that splits a list into two halves by calculating its length:
```
halves : List a -> (List a, List a)
```
If you have implemented this correctly, you should see the following:
```
*ex_10_1> halves [1..10] ([1, 2, 3, 4, 5], [6, 7, 8, 9, 10]) : (List Integer, List Integer) *ex_10_1> halves [1] ([], [1]) : (List Integer, List Integer)
```
Hint: Use div for dividing a Nat.

10.2. Recursive views: termination and efficiency

Mục đích của các view là cung cấp cho chúng ta những cách mới để so khớp dữ liệu, sử dụng cấu trúc with để có cú pháp ngắn gọn hơn. Khi bạn viết một hàm với view, bạn sử dụng các thành phần sau:

The original input data
A view of the input data, where the view data type is parameterized by the input data
A covering function for the view, which constructs an instance of the view for the input data

Sau đó, sử dụng cấu trúc `with`, bạn có thể thực hiện khớp mẫu trên cái nhìn. Khớp mẫu phụ thuộc mang lại cho bạn các mẫu có thông tin cho dữ liệu gốc. Bạn đã thấy hai ví dụ về điều này trong phần trước: đảo ngược một danh sách và chia một danh sách thành hai nửa cho thuật toán sắp xếp hợp nhất. Tuy nhiên, trong cả hai trường hợp, Idris không thể xác định rằng hàm kết quả là tổng quát. Hơn nữa, khi bạn đảo ngược một danh sách, hàm kết quả là không hiệu quả vì nó phải tái tạo cái nhìn ở mỗi lời gọi đệ quy.

Trong phần này, chúng ta sẽ xem xét cách giải quyết cả hai vấn đề này bằng cách định nghĩa các chế độ đệ quy để mô tả việc duyệt qua các cấu trúc dữ liệu. Hơn nữa, khi chúng ta đã định nghĩa một chế độ, chúng ta có thể tái sử dụng nó cho bất kỳ hàm nào sử dụng cùng một mô hình đệ quy. Thư viện Idris cung cấp một số chế độ hữu ích cho việc duyệt qua các cấu trúc dữ liệu, và chúng ta sẽ xem xét một số hàm ví dụ với một số trong số này. Tuy nhiên, trước tiên, chúng ta sẽ cải thiện định nghĩa của myReverse.

10.2.1.
“Snoc” lists: traversing a list in reverse

Một danh sách snoc là một danh sách mà các phần tử được thêm vào cuối danh sách, thay vì đầu danh sách. Chúng ta có thể định nghĩa chúng như sau, như một loại dữ liệu tổng quát:

data SnocList ty = Empty | Snoc (SnocList ty) ty

Snoc list terminology

Tên snoc list xuất phát từ việc tên truyền thống (xuất phát từ Lisp) cho phép toán tử thêm một phần tử vào đầu danh sách là cons. Do đó, tên cho phép toán tử thêm một phần tử vào cuối danh sách là snoc.

Sử dụng SnocList, bạn duyệt các phần tử theo thứ tự ngược lại, vì phần tử (của kiểu ty) xuất hiện sau danh sách (của kiểu SnocList ty). Bạn có thể dễ dàng tạo ra một danh sách từ SnocList nơi các phần tử đang ở thứ tự ngược lại:

reverseSnoc : SnocList ty -> List ty reverseSnoc Empty = [] reverseSnoc (Snoc xs x) = x :: reverseSnoc xs

Bạn có thể thể hiện mối quan hệ giữa SnocList và List một cách chính xác hơn bằng cách tham số hóa SnocList dựa trên List tương đương. Danh sách sau đây cho thấy cách định nghĩa SnocList theo cách này.

Listing 10.6.
The `SnocList` type, parameterized over the equivalent `List` (SnocList.idr)

Điều này rất giống với cấu trúc của ListLast, mà bạn đã định nghĩa trong phần trước. Sự khác biệt là Snoc nhận một tham số đệ quy của loại SnocList xs.

Ở đây, SnocList là một cái nhìn đệ quy, và snocList là hàm bao phủ của nó. Chúng ta sẽ đến với định nghĩa của snocList ngay, hãy trước tiên xem cách bạn có thể sử dụng điều này để triển khai myReverse:

Type— Begin by defining a helper function that takes a list, input, and its equivalent SnocList:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper input snoc = ?myReverseHelper_rhs

Define— If you case-split on snoc, you’ll get corresponding patterns for input:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper [] Empty = ?myReverseHelper_rhs_1 myReverseHelper (xs ++ [x]) (Snoc rec) = ?myReverseHelper_rhs_2

Refine— If the input is empty, you’ll return the empty list:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper [] Empty = [] myReverseHelper (xs ++ [x]) (Snoc rec) = ?myReverseHelper_rhs_2

Refine, type— Otherwise, you’ll recursively reverse xs and add the item x to the front:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper [] Empty = [] myReverseHelper (xs ++ [x]) (Snoc rec) = x :: myReverseHelper xs ?snocrec

There’s still a hole, ?snocrec, for the second argument in the recursive call. If you inspect it, you’ll see that you need the SnocList that represents xs:

 a : Type xs : List a rec : SnocList xs x : a -------------------------------------- snocrec : SnocList xs

Refine—

Fortunately, you already have a value, rec, of type SnocList xs, so you can use it directly to complete the definition:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper [] Empty = [] myReverseHelper (xs ++ [x]) (Snoc rec) = x :: myReverseHelper xs rec

Define— Finally, you can define myReverse by building a SnocList and calling myReverseHelper:
```
myReverse : List a -> List a myReverse input = myReverseHelper input (snocList input)
```

Bạn chưa thể kiểm tra điều này vì bạn chưa triển khai snocList, nhưng hiện tại hãy lưu ý cách điều này khác với việc triển khai myReverse trong phần 10.1.4, sử dụng ListLast. Điểm tương đồng là bạn tìm các mẫu cho danh sách đầu vào bằng cách khớp với một cách nhìn về đầu vào. Điểm khác biệt là cách nhìn này là đệ quy, có nghĩa là bạn không cần phải xây dựng lại cách nhìn trong mỗi cuộc gọi đệ quy; bạn đã có quyền truy cập vào nó.

Định nghĩa của myReverseHelper là tổng quát, vì tham số SnocList giảm dần trong mỗi lần gọi đệ quy.

*SnocList> :total myReverseHelper Main.myReverseHelper is Total

Bây giờ còn lại là triển khai snocList. Chừng nào bạn có thể triển khai snocList bằng cách duyệt qua danh sách chỉ một lần, bạn sẽ có một triển khai của myReverse chạy trong thời gian tuyến tính. Danh sách sau đây cho thấy một triển khai của snocList mà duyệt qua danh sách chỉ một lần, sử dụng một hàm trợ giúp với một biến tích lũy để xây dựng SnocList bằng cách thêm một phần tử một lần.

Listing 10.7.
Implementing the covering function `snocList`

Định nghĩa của snocList thì hơi phức tạp, liên quan đến cấu trúc sửa đổi (mà bạn đã thấy trong chương 8) để có được các kiểu dữ liệu ở dạng chính xác cho việc xây dựng SnocList. Bạn sẽ sử dụng lại với các hàm sau từ Prelude:

appendNilRightNeutral : (l : List a) -> l ++ [] = l appendAssociative : (l : List a) -> (c : List a) -> (r : List a) -> l ++ (c ++ r) = (l ++ c) ++ r

Như với bất kỳ định nghĩa phức tạp nào, việc cố gắng hiểu nó bằng cách thay thế các biểu thức con của định nghĩa bằng các lỗ hổng và xem loại của những lỗ hổng đó là một ý tưởng hay. Trong trường hợp này, cũng hữu ích để loại bỏ các cấu trúc viết lại và thay thế chúng bằng các lỗ hổng, để xem cách các loại cần được viết lại:

snocListHelp : SnocList input -> (xs : List a) -> SnocList (input ++ xs) snocListHelp {input} snoc [] = ?rewriteNil snoc snocListHelp {input} snoc (x :: xs) = ?rewriteCons (snocListHelp (Snoc snoc {x}) xs)

Bạn nên thấy các kiểu sau cho rewriteNil và rewriteCons:

rewriteNil : SnocList input -> SnocList (input ++ []) rewriteCons : SnocList ((input ++ [x]) ++ xs) -> SnocList (input ++ x :: xs)

Tin tốt là một khi bạn đã định nghĩa snocList, bạn có thể tái sử dụng nó cho bất kỳ hàm nào cần duyệt một danh sách theo chiều ngược lại. Hơn nữa, như bạn sẽ thấy trong ít lâu nữa, một chế độ xem SnocList cũng được định nghĩa trong thư viện Idris, cùng với một số cái khác.

10.2.2.
Recursive views and the with construct

Bây giờ bạn có một triển khai của myReverse chạy trong thời gian tuyến tính, vì nó duyệt qua danh sách một lần để xây dựng cái nhìn SnocList và sau đó duyệt qua cái nhìn SnocList một lần để xây dựng danh sách đảo ngược. Bạn cũng có thể xác nhận rằng Idris tin rằng nó là tổng quát:

*SnocList> :total myReverse Main.myReverse is Total

Định nghĩa kết quả không ngắn gọn bằng định nghĩa trước đó của myReverse, tuy nhiên, vì nó không sử dụng cấu trúc with:

myReverseHelper : (input : List a) -> SnocList input -> List a myReverseHelper [] Empty = [] myReverseHelper (xs ++ [x]) (Snoc rec) = x :: myReverseHelper xs rec myReverse : List a -> List a myReverse input = myReverseHelper input (snocList input)

Hãy xem điều gì sẽ xảy ra nếu bạn cố gắng làm như vậy:

Type, define— Begin with the following skeleton definition:

myReverse : List a -> List a myReverse input with (snocList input) myReverse input | with_pat = ?myReverse_rhs

Define— You can write the function by case splitting on with_pat to get the possible patterns for input:

myReverse : List a -> List a myReverse input with (snocList input) myReverse [] | Empty = ?myReverse_rhs_1 myReverse (xs ++ [x]) | (Snoc rec) = ?myReverse_rhs_2

Refine—

Fill in the right side as before:

myReverse : List a -> List a myReverse input with (snocList input) myReverse [] | Empty = [] myReverse (xs ++ [x]) | (Snoc rec) = x :: myReverse xs

Unfortunately, this calls the top-level reverse function, which rebuilds the view using snocList input, so you have the same problem as before:

*SnocList> :total myReverse Main.myReverse is possibly not total due to: possibly not total due to recursive path: with block in Main.myReverse, with block in Main.myReverse

Refine— Instead, when you make the recursive call, you can make the call directly to the with block, using the | notation on the right side:
```
myReverse : List a -> List a myReverse input with (snocList input) myReverse [] | Empty = [] myReverse (xs ++ [x]) | (Snoc rec) = x :: myReverse xs | rec
```
The call to myReverse xs | rec recursively calls myReverse, but bypasses the construction of snocList input and uses rec directly. The resulting definition is total, building the SnocList representation of input, and traversing that:
```
*SnocList> :total myReverse Main.myReverse is Total
```
This also has the effect of making myReverse run in linear time.

Trên thực tế, khi bạn sử dụng cấu trúc with, Idris sẽ giới thiệu một định nghĩa hàm mới cho phần thân của khối with, giống như định nghĩa của myReverseHelper mà bạn đã triển khai bằng tay trước đó.

Khi bạn viết myReverse xs | rec, điều này tương đương với việc viết myReverseHelper xs rec trong định nghĩa trước đó. Nhưng bằng cách sử dụng cấu trúc with thay vào đó, Idris sẽ tạo ra một kiểu thích hợp cho hàm trợ giúp.

Bằng cách sử dụng cấu trúc with, bạn có thể khớp mẫu và duyệt các cấu trúc dữ liệu theo nhiều cách khác nhau, với cấu trúc của việc khớp và duyệt được xác định bởi loại của một view. Hơn nữa, vì các view tự thân là các cấu trúc dữ liệu, Idris có thể đảm bảo rằng các hàm duyệt các view là tổng quát.

10.2.3.
Traversing multiple arguments: nested with blocks

Khi bạn viết định nghĩa kiểu mẫu, bạn thường muốn khớp với nhiều đầu vào cùng một lúc. Đến nay, bằng cách sử dụng cấu trúc with, bạn chỉ mới khớp với một giá trị. Nhưng giống như bất kỳ cấu trúc ngôn ngữ nào, các khối with có thể được lồng vào nhau.

Để xem cách hoạt động của điều này, hãy định nghĩa một hàm isSuffix:

isSuffix : Eq a => List a -> List a -> Bool

Kết quả của isSuffix nên là True nếu danh sách trong tham số đầu tiên là hậu tố của tham số thứ hai. Ví dụ:

*IsSuffix> isSuffix [7,8,9,10] [1..10] True : Bool *IsSuffix> isSuffix [7,8,9] [1..10] False : Bool

Bạn có thể định nghĩa hàm này bằng cách duyệt cả hai danh sách theo chiều ngược lại, thực hiện các bước sau:

Define— Start with the skeleton definition:

isSuffix : Eq a => List a -> List a -> Bool isSuffix input1 input2 = ?isSuffix_rhs

Define, refine—Next, match on the first input, using snocList so that you process the last element first:

isSuffix : Eq a => List a -> List a -> Bool isSuffix input1 input2 with (snocList input1) isSuffix [] input2 | Empty = ?isSuffix_rhs_1 isSuffix (xs ++ [x]) input2 | (Snoc rec) = ?isSuffix_rhs_2

You can rename rec to xsrec, to indicate that it’s a recursive view of xs when reversed. Then, if the first list is empty, it’s trivially a suffix of the second list:

isSuffix : Eq a => List a -> List a -> Bool isSuffix input1 input2 with (snocList input1) isSuffix [] input2 | Empty = True isSuffix (xs ++ [x]) input2 | (Snoc xsrec) = ?isSuffix_rhs_2

Define— Next, match on the second input, again using snocList to process the last element first. With the cursor over ?isSuffix_rhs_2, press Ctrl-Alt-W to add a nested with block:

isSuffix : Eq a => List a -> List a -> Bool isSuffix input1 input2 with (snocList input1) isSuffix [] input2 | Empty = True isSuffix (xs ++ [x]) input2 | (Snoc xsrec) with (snocList input2) isSuffix (xs ++ [x]) [] | (Snoc xsrec) | Empty = ?isSuffix_rhs_2 isSuffix (xs ++ [x]) (ys ++ [y]) | (Snoc xsrec) | (Snoc ysrec) = ?isSuffix_rhs_3

Refine— A non-empty list can’t be a suffix of an empty list, and if the last two elements of a list are equal, you’ll recursively check the rest of the list:

isSuffix : Eq a => List a -> List a -> Bool isSuffix input1 input2 with (snocList input1) isSuffix [] input2 | Empty = True isSuffix (xs ++ [x]) input2 | (Snoc rec) with (snocList input2) isSuffix (xs ++ [x]) [] | (Snoc rec) | Empty = False isSuffix (xs ++ [x]) (ys ++ [y]) | (Snoc rec) | (Snoc z) = if x == y then isSuffix xs ys | xsrec | ysrec else False

Note that when you call isSuffix recursively, you pass both of the recursive view arguments, xsrec and ysrec, to save recomputing them unnecessarily.

Bạn có thể xác nhận rằng định nghĩa này là tổng quát bằng cách hỏi Idris tại REPL:

*IsSuffix> :total isSuffix Main.isSuffix is Total

10.2.4.
More traversals: Data.List.Views

Để giúp bạn viết các hàm tổng quát, thư viện Idris cung cấp một số cách để duyệt qua các cấu trúc dữ liệu. Mô-đun Data.List.Views cung cấp một số cách, bao gồm cả cách nhìn SnocList mà bạn vừa thấy.

Ví dụ, danh sách 10.8 hiển thị chế độ xem SplitRec, cho phép bạn duyệt qua một danh sách một cách đệ quy, xử lý một nửa mỗi lần. Điều này tương tự với chế độ xem SplitList mà bạn đã thấy trong phần 10.1.5, nhưng với các duyệt đệ quy trên các nửa của danh sách.

Listing 10.8.
The `SplitRec` view from `Data.List.Views`

The Lazy generic type

Loại Lazy cho phép bạn hoãn một phép toán cho đến khi kết quả cần thiết. Ví dụ, một biến có kiểu Lazy Int là một phép toán mà khi được đánh giá, sẽ sản sinh ra một giá trị có kiểu Int. Idris có hai hàm tích hợp sau đây:

Delay : a -> Lazy a Force : Lazy a -> a

Khi kiểm tra kiểu, Idris sẽ tự động chèn các ứng dụng của Delay và Force khi cần thiết. Do đó, trong thực tế, bạn có thể xem Lazy như một chú thích cho biết rằng một biến chỉ được đánh giá khi kết quả của nó được yêu cầu. Bạn sẽ thấy định nghĩa của Lazy chi tiết hơn trong chương 11.

Bạn có thể sử dụng SplitRec để tái hiện mergeSort từ phần 10.1.5 dưới dạng một hàm tổng quát. Danh sách sau đây cho thấy điểm khởi đầu của chúng tôi.

Listing 10.9.
Starting point for a total implementation of `mergeSort`, using `SplitRec` (MergeSortView.idr)

Bạn có thể triển khai mergeSort bằng cách sử dụng chế độ nhìn SplitRec bằng cách thực hiện các bước sau:

Define— Begin by adding a with block, to say you’d like to write the function by using the SplitRec view:

mergeSort : Ord a => List a -> List a mergeSort input with (splitRec input) mergeSort [] | SplitRecNil = ?mergeSort_rhs_1 mergeSort [x] | SplitRecOne = ?mergeSort_rhs_2 mergeSort (lefts ++ rights) | (SplitRecPair lrec rrec) = ?mergeSort_rhs_3

Refine— The inputs [] and [x] are already sorted:

mergeSort : Ord a => List a -> List a mergeSort input with (splitRec input) mergeSort [] | SplitRecNil = [] mergeSort [x] | SplitRecOne = [x] mergeSort (lefts ++ rights) | (SplitRecPair lrec rrec) = ?mergeSort_rhs_3

Refine— For the (lefts ++ rights) case, you can sort lefts and rights recursively, and then merge the results:

mergeSort : Ord a => List a -> List a mergeSort input with (splitRec input) mergeSort [] | SplitRecNil = [] mergeSort [x] | SplitRecOne = [x] mergeSort (lefts ++ rights) | (SplitRecPair lrec rrec) = merge (mergeSort lefts | lrec) (mergeSort rights | rrec)

The | says that, in the recursive calls, you want to bypass constructing the view, because you already have appropriate views for lefts and rights.

Bạn có thể xác nhận rằng định nghĩa mới của mergeSort là tổng quát, và thử nghiệm nó trên một số ví dụ:

*MergeSortView> :total mergeSort Main.mergeSort is Total *MergeSortView> mergeSort [3,2,1] [1, 2, 3] : List Integer *MergeSortView> mergeSort [5,1,4,3,2,6,8,7,9] [1, 2, 3, 4, 5, 6, 7, 8, 9] : List Integer

Exercises

Những bài tập này sử dụng các khung nhìn được định nghĩa trong thư viện Idris trong các mô-đun Data.List.Views, Data.Vect.Views, và Data.Nat.Views. Đối với mỗi khung nhìn được đề cập trong các bài tập, sử dụng :doc để tìm hiểu về khung nhìn và chức năng bao trùm của nó.

Đối với mỗi bài tập này, hãy chắc chắn rằng Idris coi giải pháp của bạn là tổng quát.

Implement an equalSuffix function using the SnocList view defined in Data.List.Views. It should have the following type:

equalSuffix : Eq a => List a -> List a -> List a

Its behavior should be to return the maximum equal suffix of the two input lists. Here’s an example:

*ex_10_2> equalSuffix [1,2,4,5] [1..5] [4, 5] : List Integer *ex_10_2> equalSuffix [1,2,4,5,6] [1..5] [] : List Integer *ex_10_2> equalSuffix [1,2,4,5,6] [1..6] [4, 5, 6] : List Integer

Implement mergeSort for vectors, using the SplitRec view defined in Data.Vect.Views.
Write a toBinary function that converts a Nat to a String containing a binary representation of the Nat. You should use the HalfRec view defined in Data.Nat.Views. If you have a correct implementation, you should see this:
```
*ex_10_2> toBinary 42 "101010" : String *ex_10_2> toBinary 94 "1011110" : String
```
Hint: It’s okay to return an empty string if the input is Z.
Write a palindrome function that returns whether a list is the same when traversed forwards and backwards, using the VList view defined in Data.List.Views. If you have a correct implementation, you should see the following:
```
*ex_10_2> palindrome (unpack "abccba") True : Bool *ex_10_2> palindrome (unpack "abcba") True : Bool *ex_10_2> palindrome (unpack "abcb") False : Bool
```
Hint: The VList view allows you to traverse a list in linear time, processing the first and last elements simultaneously and recursing on the middle of the list.

10.3. Data abstraction: hiding the structure of data using views

Các góc nhìn bạn đã thấy cho đến nay trong chương này cho phép bạn kiểm tra và duyệt qua các cấu trúc dữ liệu theo những cách vượt ra ngoài việc khớp mẫu mặc định, đặc biệt tập trung vào Danh sách. Một cách nào đó, các góc nhìn cho phép bạn mô tả các giao diện thay thế để xây dựng các định nghĩa khớp mẫu:

Using SnocList, you can see how a list is constructed using [] and by adding a single element with ++, rather than using [] and ::.
Using SplitRec, you can see how a list is constructed as an empty list, a singleton list, or a concatenation of a pair of lists.

Tức là, bạn có thể tìm hiểu cách một giá trị được xây dựng bằng cách nhìn vào cái nhìn, thay vì nhìn trực tiếp vào các bộ tạo của giá trị đó. Trên thực tế, bạn thường không cần phải biết các bộ tạo dữ liệu của một giá trị để có thể sử dụng cái nhìn của một giá trị.

Với điều này trong tâm trí, một cách sử dụng các view trong thực tế là để ẩn đi việc biểu diễn dữ liệu trong một module, trong khi vẫn cho phép phát triển chức năng theo kiểu tương tác dựa trên kiểu dữ liệu mà sử dụng dữ liệu đó, thông qua việc phân tách trường hợp dựa trên một view của dữ liệu đó.

The origin of views

Ý tưởng về views được Philip Wadler đề xuất cho Haskell vào năm 1987, trong bài báo của ông “Views: một cách để khớp mẫu đồng sống với trừu tượng hóa dữ liệu.” Ví dụ trong phần này mang tinh thần của bài báo của Wadler, trong đó chứa nhiều ví dụ khác về việc sử dụng views trong thực tế. Views như một kiểu lập trình, sử dụng các kiểu phụ thuộc và một ký hiệu tương tự như ký hiệu with trong Idris, sau đó đã được Conor McBride và James McKinna đề xuất trong bài báo năm 2004 của họ, “The view from the left.”

Để kết thúc chương này, chúng ta sẽ xem xét ý tưởng này trong thực tiễn. Chúng ta sẽ quay lại ví dụ về kho lưu trữ dữ liệu mà chúng ta đã triển khai trong chương 4 và 6, ẩn đi việc biểu diễn dữ liệu trong một mô-đun Idris, và chỉ xuất ra những gì sau đây:

Schema descriptions, explaining the form of data in the store
A function for initializing a data store, empty
A function for adding an entry to the store, addToStore
A view for traversing the contents of the store, StoreView, along with its covering function, storeView

Không có yêu cầu nào trong số này đối với người dùng của mô-đun phải biết bất cứ điều gì về cấu trúc của cửa hàng tự nó hoặc cấu trúc của dữ liệu nằm trong đó.

Trước khi bạn triển khai một mô-đun và xuất khẩu các định nghĩa liên quan, chúng ta cần thảo luận ngắn gọn về cách mà Idris hỗ trợ trừu tượng dữ liệu trong các mô-đun.

10.3.1.
Digression: modules in Idris

Ngoại trừ một ví dụ nhỏ trong chương 2, các chương trình bạn đã viết trong cuốn sách này đều được chứa đựng trong một mô-đun chính duy nhất. Tuy nhiên, khi bạn viết các ứng dụng lớn hơn, bạn sẽ cần một cách để tổ chức mã thành các đơn vị biên dịch nhỏ hơn, và kiểm soát các định nghĩa nào được xuất ra từ các đơn vị đó.

Danh sách sau đây cho thấy một mô-đun Idris nhỏ định nghĩa loại Shape và xuất nó, cùng với các bộ dữ liệu của nó và một hàm để tính diện tích của một hình dạng.

Listing 10.10.
A module defining shapes and area calculations (Shape.idr)

Mỗi tên được định nghĩa trong mô-đun này có một tham số xuất khẩu giải thích xem tên đó có thể nhìn thấy bởi các mô-đun khác hay không. Một tham số xuất khẩu có thể là một trong các loại sau:

private—The name is not exported at all.
export—The name and type are exported, but not the definition. In the case of a data type, this means the type constructor is exported, but the data constructors are private.
public export—The name, type, and complete definition are exported. For data types, this means the data constructors are exported. For functions, this means the functions’ definitions are exported.

Nếu không có bộ điều chỉnh xuất khẩu trên định nghĩa hàm hoặc kiểu dữ liệu, Idris sẽ coi nó là riêng tư. Trong ví dụ trước, điều này có nghĩa là một module nhập Shape có thể sử dụng các tên Shape, Triangle, Rectangle, Circle và area, nhưng không thể sử dụng rectangle_area.

Exporting function definitions

Xuất định nghĩa của một hàm cũng như kiểu của nó (thông qua xuất công khai) là quan trọng nếu bạn muốn sử dụng hành vi của hàm trong một kiểu. Đặc biệt, điều này rất quan trọng cho các đồng nghĩa kiểu và các hàm ở cấp độ kiểu, mà chúng tôi đã sử dụng lần đầu tiên trong chương 6.

Danh sách tiếp theo cho thấy một phiên bản thay thế của mô-đun Shape mà giữ cho các chi tiết của kiểu dữ liệu Shape là trừu tượng, xuất khẩu kiểu nhưng không xuất khẩu các hàm dựng.

Listing 10.11.
Exporting `Shape` as an abstract data type (Shape_abs.idr)

Ở đây, chúng tôi đã xuất khẩu các hàm triangle, rectangle và circle để xây dựng Shape. Thay vì sử dụng trực tiếp các bộ dữ liệu, các mô-đun khác sẽ cần sử dụng những hàm này và sẽ không thể thực hiện ghép mẫu trên kiểu Shape, vì các bộ tạo không được xuất khẩu.

Sử dụng các modifier xuất khẩu, bạn có thể triển khai một mô-đun thực hiện các tính năng của một kho dữ liệu nhưng chỉ xuất khẩu các chức năng để tạo ra một kho, thêm các mục, và duyệt qua kho, mà không xuất khẩu bất kỳ chi tiết nào về cấu trúc của kho.

10.3.2.
The data store, revisited

Để minh họa vai trò của các khái niệm trong việc trừu tượng hóa dữ liệu, chúng tôi sẽ tạo ra một mô-đun triển khai một kho dữ liệu, xuất khẩu các chức năng để xây dựng kho dữ liệu. Chúng tôi cũng sẽ triển khai một khái niệm để kiểm tra và duyệt nội dung của kho dữ liệu.

Danh sách sau đây hiển thị mô-đun DataStore.idr. Đây là một biến thể nhẹ của bản ghi DataStore mà bạn đã triển khai trong chương 6.

Listing 10.12.
Data store, with a schema (DataStore.idr)

Thay vì lưu trữ lược đồ như một trường trong bản ghi, ở đây bạn tham số hóa bản ghi theo lược đồ của dữ liệu vì bạn không có ý định cho phép lược đồ được cập nhật.

export record DataStore (schema : Schema) where constructor MkData size : Nat items : Vect size (SchemaType schema)

Cú pháp cho việc khai báo bản ghi có tham số tương tự như cú pháp của một khai báo giao diện, với các tham số và kiểu của chúng được liệt kê sau tên bản ghi. Khai báo này sinh ra một trình tạo loại DataStore với kiểu sau đây:

DataStore : Schema -> Type

Nó cũng tạo ra các hàm để dự đoán kích thước của kho (size) và các mục trong kho (items) ra khỏi bản ghi. Các hàm có các kiểu sau:

size : DataStore schema -> Nat items : (rec : DataStore schema) -> Vect (size rec) (SchemaType schema)

Bởi vì bản ghi có bộ sửa đổi xuất khẩu export, kiểu dữ liệu DataStore có thể được nhìn thấy bởi các mô-đun khác, nhưng các hàm chiếu kích thước và mục thì không.

Danh sách 10.13 cho thấy ba hàm mà các mô-đun khác có thể sử dụng để tạo ra một cửa hàng mới, rỗng với một lược đồ cụ thể (rỗng), hoặc thêm một mục mới vào cửa hàng (addToStore). Mỗi hàm này đều có từ khóa xuất là export, có nghĩa là các mô-đun khác có thể thấy tên và kiểu của chúng nhưng không có quyền truy cập vào định nghĩa của chúng.

Listing 10.13.
Functions for accessing the store (DataStore.idr)

export empty : DataStore schema empty = MkData 0 [] export addToStore : (value : SchemaType schema) -> (store : DataStore schema) -> DataStore schema addToStore value (MkData _ items) = MkData _ (value :: items)

Để có thể sử dụng mô-đun này một cách hiệu quả, bạn cũng cần phải duyệt qua các mục trong cửa hàng. Bạn có thể xây dựng nội dung của một cửa hàng bằng cách sử dụng hàm empty để tạo một cửa hàng mới và addToStore để thêm một mục mới. Do đó, sẽ thuận tiện nếu bạn có thể sử dụng những điều này như các mẫu để so khớp nội dung của một cửa hàng. Khi bạn so khớp với một cửa hàng, bạn sẽ cần xử lý hai trường hợp sau:

An empty case that matches a store with no contents
An addToStore value store case that matches a store where the first entry is given by value, and the remaining items in the store are given by store

Để phù hợp với những trường hợp này, bạn có thể viết một view của DataStore.

10.3.3.
Traversing the store’s contents with a view

Danh sách 10.14 cho thấy một cái nhìn StoreView và chức năng bao phủ của nó, storeView. Chúng cho phép bạn duyệt qua nội dung của một cửa hàng bằng cách xem cách mà cửa hàng được xây dựng, có thể là với empty hoặc addToStore.

Listing 10.14.
A view for traversing the entries in a store (DataStore.idr)

Giao diện StoreView cho bạn quyền truy cập vào nội dung của cửa hàng thông qua việc khớp mẫu nhưng ẩn đi cấu trúc nội bộ của nó. Để sử dụng cửa hàng và duyệt qua nội dung của nó, bạn không cần biết bất kỳ điều gì về cấu trúc nội bộ.

Để minh họa điều này, hãy thiết lập một số dữ liệu kiểm tra và viết một số hàm để kiểm tra nó. Danh sách tiếp theo định nghĩa một cửa hàng và làm đầy nó với một số dữ liệu kiểm tra, ánh xạ tên hành tinh với tên của tàu vũ trụ đã thăm hành tinh đó lần đầu tiên và năm thăm.

Sure! Please provide the text you would like to have translated into Vietnamese.
We won’t, however, get into any debates about whether Pluto is a planet here.

Listing 10.15.
A datastore populated with some test data (TestStore.idr)

import DataStore testStore : DataStore (SString .+. SString .+. SInt) testStore = addToStore ("Mercury", "Mariner 10", 1974) (addToStore ("Venus", "Venera", 1961) (addToStore ("Uranus", "Voyager 2", 1986) (addToStore ("Pluto", "New Horizons", 2015) empty)))

The application operator $

Khi các biểu thức trở nên lồng ghép sâu, như trong định nghĩa testStore, có thể rất khó để theo dõi cấu trúc dấu ngoặc. Toán tử $ là một toán tử ở giữa áp dụng một hàm cho một đối số, và bạn có thể sử dụng nó để giảm bớt nhu cầu về dấu ngoặc.

Sử dụng nó, bạn có thể viết những điều sau:

testStore = addToStore ("Mercury", "Mariner 10", 1974) $ addToStore ("Venus", "Venera", 1961) $ addToStore ("Uranus", "Voyager 2", 1986) $ addToStore ("Pluto", "New Horizons", 2015) $ empty

Việc viết $ do đó tương đương với việc đặt phần còn lại của biểu thức trong dấu ngoặc. Ví dụ, việc viết f x $ y z hoàn toàn tương đương với việc viết f x (y z).

Danh sách dưới đây hiển thị một quá trình duyệt cơ bản của kho dữ liệu, trả về danh sách các mục trong kho.

Listing 10.16.
A function to convert the store’s contents to a list of entries (TestStore.idr)

Nếu bạn gọi showItems với dữ liệu thử nghiệm, bạn sẽ thấy kết quả sau:

*TestStore> listItems testStore [("Mercury", "Mariner 10", 1974), ("Venus", "Venera", 1961), ("Uranus", "Voyager 2", 1986), ("Pluto", "New Horizons", 2015)] : List (String, String, Int)

Hơn nữa, bạn có thể muốn viết các hàm đi qua kho dữ liệu và lọc ra một số mục nhất định. Ví dụ, giả sử bạn muốn lấy danh sách các hành tinh đã được khám phá lần đầu bởi một tàu vũ trụ trong thế kỷ xx. Bạn có thể làm điều này bằng cách viết hàm sau:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String

Bạn có thể nghĩ về một sơ đồ có dạng (SString .+. val_schema) như cung cấp một cặp khóa-giá trị, trong đó khóa là một String và val_schema mô tả hình thức của các giá trị. Sau đó, filterKeys sẽ áp dụng một hàm cho giá trị trong cặp, và nếu nó trả về True, nó sẽ thêm khóa vào một danh sách String. Điều này có thể tìm ra các hành tinh mà một tàu thăm dò đã đến thăm trước năm 2000:

*TestStore> filterKeys (\x => snd x < 2000) testStore ["Mercury", "Venus", "Uranus"] : List String

Bạn có thể thực hiện filterKeys bằng cách sử dụng StoreView theo các bước sau:

Type, define—Begin with a type and a skeleton definition:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String filterKeys test input = ?filterKeys_rhs

Define— You’ll define the function by traversing the store using StoreView, so you can use the with construct to build the view, and case-split on it:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String filterKeys test input with (storeView input) filterKeys test empty | SNil = ?filterKeys_rhs_1 filterKeys test (addToStore value store) | (SAdd rec) = ?filterKeys_rhs_2

Refine— If the store is empty, there’s no value to apply the test to, so return an empty list:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String filterKeys test input with (storeView input) filterKeys test empty | SNil = [] filterKeys test (addToStore value store) | (SAdd rec) = ?filterKeys_rhs_2

Refine— Otherwise, because of the schema of the data store, entry must itself be a key-value pair:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String filterKeys test input with (storeView input) filterKeys test empty | SNil = [] filterKeys test (addToStore (key, value) store) | (SAdd rec) = ?filterKeys_rhs_2

You’ll apply test to the value. If the result is True, you’ll keep the key and recursively build the rest of the list. If the result is False, you’ll omit the key and build the rest of the list:

filterKeys : (test : SchemaType val_schema -> Bool) -> DataStore (SString .+. val_schema) -> List String filterKeys test input with (storeView input) filterKeys test empty | SNil = [] filterKeys test (addToStore (key, value) store) | (SAdd rec) = if test value then key :: filterKeys test store | rec else filterKeys test store | rec

You can try this function with some test filters:

*TestStore> filterKeys (\x => fst x == "Voyager 2") testStore ["Uranus"] : List String *TestStore> filterKeys (\x => snd x > 2000) testStore ["Pluto"] : List String *TestStore> filterKeys (\x => snd x < 2000) testStore ["Mercury", "Venus", "Uranus"] : List String

For both showItems and filterKeys, you’ve written a function that traverses the contents of the data store without knowing anything about the internal representation of the store. In each case, you’ve used a view to deconstruct the data, rather than deconstructing the data directly. If you were to change the internal representation in the DataStore module, and correspondingly the implementation of storeView, the implementations of showItems and filterKeys would remain unchanged.

Exercises

Write a getValues function that returns a list of all values in a DataStore. It should have the following type:
```
getValues : DataStore (SString .+. val_schema) -> List (SchemaType val_schema)
```
You can test your definition by writing a function to set up a data store:
```
testStore : DataStore (SString .+. SInt) testStore = addToStore ("First", 1) $ addToStore ("Second", 2) $ empty
```
If you’ve implemented getValues correctly, you should see the following:
```
*ex_10_3> getValues testStore [1, 2] : List Int
```

Define a view that allows other modules to inspect the abstract Shape data type in listing 10.11. You should be able to use it to complete the following definition:

area : Shape -> Double area s with (shapeView s) area (triangle base height) | STriangle = ?area_rhs_1 area (rectangle width height) | SRectangle = ?area_rhs_2 area (circle radius) | SCircle = ?area_rhs_3

If you have implemented this correctly, you should see the following:

*ex_10_3> area (triangle 3 4) 6.0 : Double *ex_10_3> area (circle 10) 314.1592653589793 : Double

10.4. Summary

A view is a dependent type that describes the possible forms of another data type. Views take advantage of dependent pattern matching to allow you to extend the forms of patterns you can use.
A covering function builds a view of a value. By convention, its name is the name of the view with an initial lowercase letter.
The with construct allows you to use views directly, without defining an intermediate function.
You can use views to define alternative traversals of data structures, such as extracting the last element of a list instead of the first.
Recursive views help you write functions that are guaranteed to terminate, by writing recursive functions that pattern-match on the view.
Idris provides several views for alternative traversals of List in the Data.List.Views library. Similar libraries exist for Vect, Nat, and String.
You can hide the structure of data in a module, while still supporting interactive type-driven programming with that data, by exporting views for traversing data structures.

Part 3.
Idris and the real world

Trong phần 2, bạn đã có được kinh nghiệm trong việc phát triển các chương trình một cách tương tác, được hướng dẫn bởi các kiểu dữ liệu, và bạn đã tìm hiểu về tất cả các tính năng cốt lõi của Idris. Bây giờ, đã đến lúc áp dụng những gì bạn đã học vào một số ví dụ thực tiễn hơn.

Đầu tiên, trong chương 11, bạn sẽ tìm hiểu về việc viết các chương trình xử lý các cấu trúc có thể vô hạn như dòng dữ liệu. Bạn đã biết về tầm quan trọng của việc viết các hàm toàn phần, nhưng trong chương 11, bạn sẽ thấy rằng tính toàn phần không chỉ liên quan đến sự kết thúc. Một hàm cũng được coi là toàn phần nếu nó sản xuất một phần nào đó của một kết quả có thể vô hạn, điều này có nghĩa là bạn có thể viết các hệ thống tương tác như máy chủ và vòng lặp đọc - đánh giá - in kết quả mà chạy mãi mãi, nhưng vẫn luôn toàn phần.

Chương 12–14 đề cập đến trạng thái. Các chương trình thực tế thường cần phải xử lý trạng thái toàn cầu theo một cách nào đó, và bạn sẽ thấy cách biểu diễn trạng thái cũng như cách mô tả các thuộc tính của trạng thái sao cho bạn có thể đảm bảo rằng các chương trình tuân theo các giao thức một cách chính xác. Nếu bạn đang triển khai một hệ thống có các thuộc tính bảo mật quan trọng, chẳng hạn như một máy ATM cho ngân hàng, bạn có thể sử dụng phát triển theo kiểu để đảm bảo rằng các thuộc tính đó được thỏa mãn.

Cuối cùng, chương 15 cung cấp một ví dụ mở rộng về phát triển dựa trên kiểu, cho thấy cách triển khai một thư viện cho lập trình đồng thời với các kiểu. Bạn sẽ bắt đầu bằng việc viết một kiểu đơn giản để nắm bắt một vấn đề lập trình đồng thời cụ thể, sau đó dần dần tinh chỉnh nó để nắm bắt nhiều thuộc tính quan trọng hơn của các chương trình đồng thời.

Chapter 11.
Streams and processes: working with infinite data

Chương này đề cập đến

Generating and processing streams of data
Distinguishing terminating from productive total functions
Defining total interactive processes using infinite streams

Các hàm mà chúng tôi đã viết trong cuốn sách này cho đến nay hoạt động ở chế độ xử lý theo lô, xử lý tất cả các đầu vào của chúng và sau đó trả về một đầu ra. Trong chương trước, chúng tôi cũng đã dành một chút thời gian để thảo luận về tầm quan trọng của việc kết thúc, và bạn đã học cách sử dụng các quan điểm để giúp bạn viết chương trình đảm bảo sẽ kết thúc.

Nhưng dữ liệu đầu vào không phải lúc nào cũng đến theo lô, và bạn sẽ thường muốn viết các chương trình không kết thúc, chạy liên tục. Ví dụ, sẽ tiện lợi khi coi dữ liệu đầu vào cho một chương trình tương tác (chẳng hạn như các lần nhấn phím, chuyển động chuột, v.v.) như một luồng dữ liệu liên tục, được xử lý từng phần tử một, dẫn đến một luồng dữ liệu đầu ra. Trên thực tế, nhiều chương trình về cơ bản là các bộ xử lý luồng:

A read-eval-print loop, such as the Idris environment, processes a potentially infinite stream of user commands, giving an output stream of responses.
A web server processes a potentially infinite stream of HTTP requests, giving an output stream of responses to be sent over the network.
A real-time game processes a potentially infinite stream of commands from a controller, giving an output stream of audiovisual actions.

Hơn nữa, ngay cả khi bạn đang viết các hàm thuần túy không tương tác với các nguồn dữ liệu hoặc thiết bị bên ngoài, các luồng cho phép bạn viết các thành phần chương trình tái sử dụng bằng cách tách biệt việc sản xuất dữ liệu ra khỏi việc tiêu thụ dữ liệu. Ví dụ, giả sử bạn đang viết một hàm để xác định căn bậc hai của một số. Bạn có thể làm điều này bằng cách sản xuất một danh sách vô hạn các xấp xỉ ngày càng gần với một giải pháp, và sau đó viết một hàm riêng để tiêu thụ danh sách đó, tìm xấp xỉ đầu tiên trong các giới hạn mong muốn.

Producing and consuming data

Một chủ đề phổ biến trong chương này là sự phân biệt giữa các chương trình tiêu thụ (hoặc xử lý) dữ liệu và các chương trình sản xuất dữ liệu. Tất cả các hàm bạn đã thấy trong cuốn sách này cho đến nay đều là các trình tiêu thụ dữ liệu, và trong chương trước, chúng ta đã xem xét việc sử dụng các view để giúp chúng ta viết các hàm đảm bảo sẽ kết thúc khi tiêu thụ dữ liệu. Tuy nhiên, khi bạn viết các hàm kết thúc, việc tiêu thụ dữ liệu chỉ là một phần của câu chuyện: một hàm tạo ra một luồng vô hạn sẽ không bao giờ kết thúc, sau cùng. Như bạn sẽ thấy, Idris kiểm tra rằng các hàm tạo ra luồng được đảm bảo là sản xuất, để bất kỳ hàm nào tiêu thụ đầu ra của một bộ tạo luồng sẽ luôn có dữ liệu để xử lý.

Các loại chương trình chúng ta viết trong thực tế thường có một thành phần kết thúc, xử lý và phản hồi với đầu vào của người dùng, và một thành phần không kết thúc, là một vòng lặp vô hạn gọi lại thành phần kết thúc. Trong chương này, bạn sẽ thấy cách viết các chương trình quản lý sự phân biệt này, cả sản xuất và tiêu thụ dữ liệu có thể vô hạn. Chúng ta sẽ bắt đầu với một trong những cấu trúc vô hạn phổ biến nhất, đó là dòng (streams), và sau đó sẽ xem xét cách định nghĩa các hàm tổng quát mô tả các hàm tương tác thực hiện vô thời hạn.

11.1. Streams: generating and processing infinite lists

Dòng dữ liệu là các chuỗi giá trị vô hạn, và bạn có thể xử lý từng giá trị một. Trong phần này, bạn sẽ thấy cách viết các hàm tạo ra một chuỗi dữ liệu vô hạn, theo yêu cầu, và cách viết các hàm tiêu thụ một phần dữ liệu hữu hạn được sản xuất dưới dạng dòng.

Làm ví dụ đầu tiên, để minh họa cho những ý tưởng đằng sau các dòng, chúng ta sẽ xem xét cách tạo ra một chuỗi số vô hạn, 0, 1, 2, 3, 4, ..., và cách xử lý chúng theo nhu cầu để gán nhãn cho các phần tử trong một danh sách, như được minh họa trong hình 11.1.

Figure 11.1.
Labeling the elements of a `List` by taking elements from an infinite stream of numbers. The stream contains an infinite number of elements, but you only take as many as you need to label the elements in the finite list.

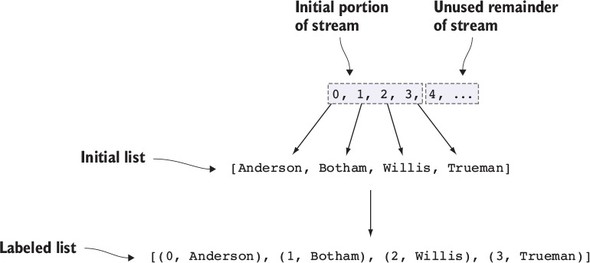
Bạn có thể sử dụng một hàm như vậy sau khi sắp xếp một số dữ liệu, ví dụ, để gán một chỉ mục rõ ràng cho dữ liệu. Như bạn sẽ thấy, bạn có thể sử dụng luồng để tách biệt một cách rõ ràng việc tạo ra một danh sách nhãn vô hạn khỏi việc tiêu thụ các nhãn mà bạn cần cho một danh sách đầu vào cụ thể.

Ngoài việc chỉ cho bạn cách định nghĩa các loại dữ liệu có thể vô hạn, tôi cũng sẽ giới thiệu loại dữ liệu Stream, được cung cấp bởi Prelude, và chúng ta sẽ nhanh chóng xem qua một số hàm trên Stream. Cuối cùng, chúng ta sẽ xem một ví dụ lớn hơn sử dụng một luồng số ngẫu nhiên để triển khai một trò chơi số học.

11.1.1.
Labeling elements in a List

Giả sử bạn muốn viết một hàm gán nhãn cho mỗi phần tử của một danh sách với một số nguyên chỉ vị trí của nó trong danh sách, như trong hình 11.1. Tức là, cái gì đó như thế này:

label : List a -> List (Integer, a)

Chạy hàm này trên một số ví dụ sẽ cho kết quả sau:

*Streams> label ['a', 'b', 'c'] [(0, 'a'), (1, 'b'), (2, 'c')] : List (Integer, Char) *Streams> label ["Anderson", "Botham", "Willis", "Trueman"] [(0, "Anderson"), (1, "Botham"), (2, "Willis"), (3, "Trueman")] : List (Integer, String)

Danh sách dưới đây cho thấy một cách để ghi nhãn bằng cách viết một hàm trợ giúp, labelFrom, nhận nhãn cho phần tử đầu tiên của danh sách, sau đó ghi nhãn cho phần còn lại của danh sách, tăng nhãn lên.

Listing 11.1.
Labeling each element of a list with an integer (Label.idr)

Điều này hoạt động như mong đợi, nhưng định nghĩa của labelFrom kết hợp hai thành phần: gán nhãn cho từng phần tử và tạo ra nhãn đó. Một cách viết thay thế cho label sẽ cho phép bạn tái sử dụng hai thành phần này một cách riêng biệt—bạn có thể viết hai hàm:

countFrom—Generates an infinite stream of numbers, counting upwards from a given starting point.
labelWith—Takes an infinite stream of labels, and pairs each label with a corresponding element in a finite list. It therefore only consumes as much of the infinite stream as necessary to label the elements in the list.

Một cách tự nhiên để cố gắng viết countFrom có thể là tạo ra một Danh sách các số nguyên từ một điểm bắt đầu nhất định:

countFrom : Integer -> List Integer countFrom n = n :: countFrom (n + 1)

Khi Idris chạy một chương trình đã biên dịch, tuy nhiên, nó sẽ đánh giá hoàn toàn các đối số của một hàm trước khi đánh giá hàm đó. Vì vậy, thật không may, nếu bạn cố gắng truyền kết quả của countFrom cho một hàm mà mong đợi một Danh sách, hàm đó sẽ không bao giờ chạy vì kết quả của countFrom sẽ không bao giờ được đánh giá hoàn toàn. Nếu bạn hỏi Idris xem định nghĩa này của countFrom có tổng quát hay không, nó sẽ cho bạn biết rằng có một vấn đề:

*StreamFail> :total countFrom Main.countFrom is possibly not total due to recursive path: Main.countFrom, Main.countFrom

Bạn có thể thấy rằng countFrom sẽ không bao giờ kết thúc, vì nó thực hiện một cuộc gọi đệ quy cho mỗi đầu vào, nhưng để viết labelWith, bạn chỉ cần một phần hữu hạn của kết quả của countFrom. Những gì bạn thực sự cần biết về countFrom, do đó, không phải là nó luôn kết thúc, mà là nó sẽ luôn tạo ra nhiều số như bạn cần. Có nghĩa là, bạn cần biết rằng nó là năng suất và được đảm bảo sẽ tạo ra một chuỗi số dài vô hạn.

Như bạn sẽ thấy ở phần tiếp theo, bạn có thể sử dụng kiểu để phân biệt giữa những biểu thức mà việc đánh giá được đảm bảo sẽ kết thúc và những biểu thức mà việc đánh giá được đảm bảo sẽ tiếp tục tạo ra các giá trị mới, đánh dấu các tham số của một cấu trúc dữ liệu là có thể vô hạn.

11.1.2.
Producing an infinite list of numbers

Để tạo ra một danh sách vô hạn các số và chỉ tiêu thụ phần hữu hạn của danh sách mà bạn cần, bạn có thể sử dụng một kiểu dữ liệu mới, Inf, để đánh dấu các phần có khả năng vô hạn của cấu trúc.

Bạn sẽ thấy thêm chi tiết về cách Inf hoạt động trong thời gian ngắn. Trước tiên, hãy cùng xem xét một kiểu dữ liệu của danh sách vô hạn sử dụng Inf.

Listing 11.2.
A data type of infinite lists (InfList.idr)

InfList tương tự như kiểu tổng quát List, với hai sự khác biệt quan trọng:

There’s no Nil constructor, only a (::) constructor, so there’s no way to end the list.
The recursive argument is wrapped in a new data type, Inf, that marks the argument as potentially infinite.

Để thao tác với các phép tính có thể vô hạn, bạn có thể sử dụng các hàm Delay và Force. Danh sách 11.3 cung cấp các kiểu của Delay và Force. Ý tưởng là bạn có thể sử dụng Delay và Force để kiểm soát chính xác khi nào một biểu thức con được đánh giá, để chỉ tính toán phần hữu hạn của một danh sách vô hạn cần thiết cho một hàm cụ thể.

Listing 11.3.
The `Inf` abstract data type, for delaying potentially infinite computations

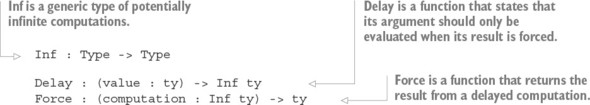
Danh sách dưới đây cho thấy cách bạn có thể định nghĩa countFrom, tạo ra một danh sách vô hạn các số nguyên từ một giá trị khởi đầu nhất định.

Listing 11.4.
Defining `countFrom` as an infinite list (InfList.idr)

Nếu bạn thử đánh giá countFrom 0 tại REPL để tạo ra một danh sách vô hạn đếm lên từ 0, bạn sẽ thấy tác động của Delay:

*InfList> countFrom 0 0 :: Delay (countFrom 1) : InfList Integer

Bạn có thể thấy rằng bộ đánh giá Idris đã để đối số cho Delay chưa được đánh giá. Bộ đánh giá xử lý Force và Delay một cách đặc biệt: nó chỉ đánh giá một đối số cho Delay khi được yêu cầu một cách rõ ràng bởi một Force. Kết quả là, mặc dù có một cuộc gọi đệ quy đến countFrom trên mọi đầu vào, quá trình đánh giá ở REPL vẫn kết thúc. Idris thậm chí còn đồng ý rằng nó là tổng quát:

*InfList> :total countFrom Main.countFrom is Total

Terminology: recursion and corecursion, data and codata

Bạn có thể nghe các lập trình viên Idris đề cập đến các hàm như countFrom là đồng đệ quy (corecursive) thay vì đệ quy (recursive), và các danh sách vô hạn là đồng dữ liệu (codata) thay vì dữ liệu (data). Sự phân biệt giữa dữ liệu và đồng dữ liệu là dữ liệu là hữu hạn và được sử dụng, trong khi đồng dữ liệu là tiềm năng vô hạn và được sản xuất. Trong khi đệ quy hoạt động bằng cách lấy dữ liệu và phân tích nó xuống một trường hợp cơ bản, đồng đệ quy hoạt động bằng cách bắt đầu từ một trường hợp cơ bản và xây dựng đồng dữ liệu.

Có thể có vẻ ngạc nhiên rằng Idris coi countFrom là tổng quát, mặc dù nó sản sinh ra một cấu trúc vô hạn. Trước khi chúng ta tiếp tục thảo luận về cách làm việc với danh sách vô hạn, do đó, điều đáng để xem xét kỹ lưỡng hơn là ý nghĩa của việc một hàm là tổng quát.

11.1.3.
Digression: what does it mean for a function to be total?

Nếu một hàm là tổng quát, nó sẽ không bao giờ gặp lỗi do thiếu trường hợp (tức là tất cả các đầu vào hợp lệ đều được bao phủ), và nó sẽ luôn trả về kết quả hợp lệ trong một khoảng thời gian hữu hạn. Các hàm mà bạn đã viết trong các chương trước đều nhận dữ liệu hữu hạn làm đầu vào, vì vậy chúng là tổng quát miễn là chúng hoàn thành cho mọi đầu vào. Nhưng giờ bạn đã thấy kiểu Inf, bạn có thể viết các hàm sản xuất dữ liệu vô hạn, và những hàm này không hoàn thành! Do đó, chúng ta sẽ cần phải tinh chỉnh hiểu biết của mình về ý nghĩa của việc một hàm là tổng quát.

Các hàm tạo ra dữ liệu vô hạn có thể được sử dụng như các thành phần của hàm kết thúc, với điều kiện chúng luôn cung cấp một mảnh dữ liệu mới theo yêu cầu. Trong trường hợp của countFrom, nó sẽ luôn tạo ra một số nguyên mới trước khi thực hiện một cuộc gọi đệ quy trì hoãn.

Hình 11.2 minh họa cấu trúc của countFrom. Lời gọi đệ quy bị hoãn của countFrom là một đối số cho (::), có nghĩa là countFrom sẽ luôn tạo ra ít nhất một phần tử của danh sách vô hạn trước khi thực hiện một lời gọi đệ quy. Do đó, bất kỳ hàm nào tiêu thụ kết quả từ countFrom sẽ luôn có dữ liệu để làm việc.

Figure 11.2.
Producing values of an infinite structure. The `Delay` means that Idris will only make the recursive call to `countFrom` when it’s required by `Force`.

Total functions defined

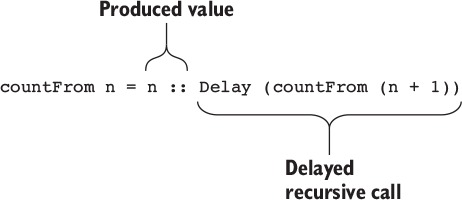
Một hàm toàn phần là một hàm mà, cho tất cả các đầu vào có kiểu đúng, thực hiện một trong các hành động sau:

Terminates with a well-typed result
Produces a non-empty finite prefix of a well-typed infinite result in finite time

Chúng ta có thể mô tả các hàm tổng quát là hoặc dừng hoặc sản xuất. Vấn đề dừng là khó khăn trong việc xác định liệu một chương trình cụ thể có dừng lại hay không, và nhờ vào Alan Turing, chúng ta biết rằng về cơ bản là không thể viết một chương trình giải quyết vấn đề dừng. Nói cách khác, Idris không thể xác định liệu một trong các điều kiện này có đúng cho tất cả các hàm tổng quát hay không. Thay vào đó, nó thực hiện một sự xấp xỉ bảo thủ bằng cách phân tích cú pháp của một hàm.

Idris coi một hàm là toàn phần nếu có các mẫu bao phủ tất cả các đầu vào có kiểu hợp lệ và nó có thể xác định rằng một trong các điều kiện sau đây đúng:

When there’s a recursive call (or a sequence of mutually recursive calls), there’s a decreasing argument that converges toward a base case.
When there’s a recursive call as an argument to Delay, the delayed call will always be an argument to a data constructor (or sequence of nested data constructors) after evaluation, for all inputs.

Chúng tôi đã thảo luận về điều kiện đầu tiên trong chương trước. Điều kiện thứ hai cho phép chúng tôi sử dụng các hàm như countFrom trong một hàm kết thúc. Để minh họa rõ hơn, thật hữu ích khi xem cách danh sách vô hạn kết quả được sử dụng. Như một ví dụ, hãy viết một hàm tiêu thụ một tiền tố dài hữu hạn của một InfList.

11.1.4.
Processing infinite lists

Một hàm tạo ra một danh sách vô hạn là toàn phần nếu nó đảm bảo tiếp tục sản xuất dữ liệu mỗi khi dữ liệu được yêu cầu. Bạn có thể thấy điều này hoạt động bằng cách viết một chương trình tính toán danh sách hữu hạn từ phần tiền tố của một danh sách vô hạn:

getPrefix : (count : Nat) -> InfList ty -> List ty

getPrefix trả về một danh sách bao gồm count phần tử đầu tiên từ một danh sách vô hạn. Nó hoạt động bằng cách đệ quy lấy phần tử tiếp theo từ danh sách vô hạn miễn là nó cần thêm phần tử. Bạn có thể định nghĩa nó theo các bước sau:

Define— First, case-split on the count argument:

getPrefix : (count : Nat) -> InfList a -> List a getPrefix Z xs = ?getPrefix_rhs_1 getPrefix (S k) xs = ?getPrefix_rhs_2

Refine— If you’re taking zero elements from the infinite list, return an empty list:

getPrefix : (count : Nat) -> InfList a -> List a getPrefix Z xs = [] getPrefix (S k) xs = ?getPrefix_rhs_2

Define— If you’re taking more than one element, you’ll case-split on the infinite list and then add the first value in the infinite list as the first element of the result.
```
getPrefix : (count : Nat) -> InfList a -> List a getPrefix Z xs = [] getPrefix (S k) (value :: xs) = value :: ?getPrefix_rhs_1
```
Type, refine—If you look at the type of the hole, ?getPrefix_rhs_1, you’ll see the following:
```
 a : Type k : Nat value : a xs : Inf (InfList a) -------------------------------------- getPrefix_rhs_1 : List a
```
You can see from the type of xs that it’s an infinite list that has not yet been computed, because it’s an infinite list wrapped in an Inf. To complete the definition, you can Force the computation of xs and recursively get its prefix:
```
getPrefix : (count : Nat) -> InfList a -> List a getPrefix Z xs = [] getPrefix (S k) (value :: xs) = value :: getPrefix k (Force xs)
```

Định nghĩa thu được là tổng quát, theo Idris:

*InfList> :total getPrefix Main.getPrefix is Total

Mặc dù một trong các đầu vào có khả năng là vô hạn, getPrefix chỉ đánh giá nhiều như cần thiết để lấy count phần tử từ danh sách vô hạn. Bởi vì count là một số hữu hạn, getPrefix sẽ luôn kết thúc miễn là InfList được đảm bảo tiếp tục sản xuất các phần tử mới.

Trong thực tế, bạn có thể bỏ qua các lời gọi đến Delay và Force và để Idris tự thêm chúng khi cần. Nếu, trong quá trình kiểm tra kiểu, Idris gặp một giá trị có kiểu Inf ty khi nó cần một giá trị có kiểu ty, nó sẽ thêm một lời gọi ngầm định đến Force. Tương tự, nếu nó gặp một ty khi nó cần một Inf ty, nó sẽ thêm một lời gọi ngầm định đến Delay. Danh sách sau đây cho thấy cách bạn có thể định nghĩa countFrom và getPrefix bằng cách sử dụng Force và Delay ngầm định.

Listing 11.5.
Taking a finite portion of an infinite list, with implicit `Force` and `Delay` (InfList.idr)

Do đó, bạn có thể coi Inf như một chú thích trên một kiểu dữ liệu, đánh dấu các phần của một cấu trúc dữ liệu có thể là vô hạn, và để trình kiểm tra kiểu của Idris quản lý các chi tiết về khi nào các phép toán phải được trì hoãn hoặc buộc phải thực hiện.

Bây giờ bạn đã thấy cách tách biệt sự sản xuất dữ liệu, sử dụng countFrom để tạo ra một danh sách vô hạn các số, khỏi việc tiêu thụ dữ liệu, sử dụng một hàm như getPrefix, chúng ta có thể xem lại định nghĩa của nhãn. Thay vì sử dụng loại dữ liệu InfList của riêng chúng ta và countFrom, chúng ta sẽ sử dụng một loại dữ liệu được định nghĩa trong Prelude cho mục đích này: Stream.

11.1.5.
The Stream data type

Danh sách 11.6 cho thấy định nghĩa của Stream trong Prelude. Nó có cùng cấu trúc với định nghĩa của InfList mà bạn đã thấy trong phần trước. Thêm vào đó, Prelude cung cấp một số hàm hữu ích để xây dựng và xử lý Streams, một số trong đó cũng được hiển thị trong danh sách này.

Listing 11.6.
The `Stream` data type and some functions, defined in the Prelude

Bạn có thể thấy các hàm lặp lại, lấy và lặp lại hoạt động tại REPL. Ví dụ, hàm lặp lại tạo ra một chuỗi vô hạn của một phần tử, được trì hoãn cho đến khi được yêu cầu cụ thể:

Idris> repeat 94 94 :: Delay (repeat 94) : Stream Integer

Giống như getPrefix trên InfList, take lấy một phần tiền tố của một Stream có độ dài cụ thể.

Idris> take 10 (repeat 94) [94, 94, 94, 94, 94, 94, 94, 94, 94, 94] : List Integer

`lặp lại áp dụng một hàm nhiều lần, tạo ra một chuỗi các kết quả. Ví dụ, bắt đầu từ 0 và áp dụng liên tục (+1) dẫn đến một chuỗi số nguyên tăng dần, như countFrom:`

Idris> take 10 (iterate (+1) 0) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] : List Integer

Syntactic sugar for stream generation

Idris cung cấp một cú pháp ngắn gọn để tạo ra các chuỗi số, tương tự như cú pháp cho danh sách.

Idris> take 10 [1..] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] : List Integer

Cú pháp [1..] tạo ra một Stream đếm lên từ 1. Điều này hoạt động cho bất kỳ loại số đếm được nào, như trong ví dụ sau:

Idris> the (List Int) take 10 [1..] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] : List Int

Bạn cũng có thể thay đổi khoảng tăng.

Idris> the (List Int) (take 10 [1,3..]) [1, 3, 5, 7, 9, 11, 13, 15, 17, 19] : List Int

Tổng hợp lại tất cả những điều này, danh sách sau đây cho thấy cách định nghĩa nhãn bằng cách sử dụng iterate để tạo ra một chuỗi nhãn số nguyên vô hạn, và một hàm labelWith tiêu tốn đủ một chuỗi nhãn vô hạn để gán nhãn cho mỗi phần tử của một danh sách.

Listing 11.7.
Labeling each element of a `List` using a `Stream` (Streams.idr)

Theo định nghĩa này, bạn tách biệt hai thành phần của việc tạo nhãn và gán nhãn cho mỗi phần tử trong danh sách.

Bạn thậm chí có thể cho phép một kiểu tổng quát hơn cho labelWith, nhận một Stream labelType thay vì một Stream Integer, và cho phép gán nhãn bằng bất kỳ kiểu nào mà bạn có thể tạo ra một Stream. Ví dụ, hàm cycle tạo ra một Stream lặp lại một chuỗi nhất định:

*Streams> take 10 $ cycle ["a", "b", "c"] ["a", "b", "c", "a", "b", "c", "a", "b", "c", "a"] : List String

Sử dụng vòng lặp để tạo ra một luồng, bạn có thể gán nhãn cho từng phần tử của một danh sách bằng một chuỗi nhãn tuần hoàn, lặp lại nhiều lần nếu cần để gán nhãn cho toàn bộ danh sách:

*Streams> labelWith (cycle ["a", "b", "c"]) [1..5] [("a", 1), ("b", 2), ("c", 3), ("a", 4), ("b", 5)] : List (String, Integer)

11.1.6.
An arithmetic quiz using streams of random numbers

Bạn có thể sử dụng Stream trong bất kỳ tình huống nào khi bạn cần một nguồn dữ liệu nhưng không biết trước bạn sẽ cần tạo ra bao nhiêu dữ liệu. Ví dụ, bạn có thể viết một bài kiểm tra toán học tương tác cần một nguồn số để đưa ra các câu hỏi. Danh sách sau đây cho thấy cách bạn có thể làm điều này.

Listing 11.8.
An arithmetic quiz, taking a `Stream` of numbers for the questions (Arith.idr)

Chức năng kiểm tra kiến thức nhận một nguồn số nguyên vô tận và điểm số hiện tại, sau đó trả về một hành động IO hiển thị điểm số và một câu hỏi, đọc câu trả lời từ người dùng và lặp lại. Các câu hỏi phát sinh trực tiếp từ dòng dữ liệu đầu vào, vì vậy bạn có thể thử với một chuỗi các số tăng dần:

*Arith> :exec quiz (iterate (+1) 0) 0 Score so far: 0 0 * 1? 0 Correct! Score so far: 1 2 * 3? 6 Correct! Score so far: 2 4 * 5? 20 Correct! Score so far: 3

Aborting execution

Việc thực thi một chương trình lặp đi lặp lại sẽ tiếp tục cho đến khi một sự kiện bên ngoài khiến chương trình thoát. Bạn có thể hủy thực thi tại REPL bằng cách nhấn Ctrl-C.

Cho đến nay, điều này không đặc biệt thú vị vì bạn đã biết trước câu hỏi sẽ như thế nào. Thay vào đó, bạn có thể viết một hàm tạo ra một dòng các số nguyên giả ngẫu nhiên được sinh từ một hạt giống ban đầu. Danh sách dưới đây cho thấy một cách để tạo ra một dòng số có vẻ ngẫu nhiên bằng cách sử dụng bộ phát sinh đồng nhất tuyến tính.

Listing 11.9.
Generating a stream of pseudo-random numbers from a seed (Arith.idr)

Pseudo-random number generation

Hàm randoms trong danh sách 11.9 tạo ra một chuỗi số có vẻ ngẫu nhiên nhưng có thể dự đoán được từ một hạt giống ban đầu, sử dụng một bộ sinh số đồng dư tuyến tính. Đây là một trong những kỹ thuật cổ xưa nhất cho việc sinh số giả ngẫu nhiên. Nó phù hợp với mục đích của chúng ta cho ví dụ này, nhưng không thích hợp cho những tình huống yêu cầu tính ngẫu nhiên chất lượng cao, chẳng hạn như ứng dụng mã hóa, do phân bố và khả năng dự đoán của các số được sinh ra.

Bạn có thể thử chạy quiz với một chuỗi số được sinh ra ngẫu nhiên:

*Arith> :exec quiz (randoms 12345) 0 Score so far: 0 1095649041 * -2129715532? no idea Wrong, the answer is -765659660 Score so far: 0

Trước đây, các câu hỏi quá dễ đoán, nhưng bây giờ chúng có lẽ hơi khó với hầu hết chúng ta! Hơn nữa, trong ví dụ trước, kết quả thậm chí đã vượt qua giới hạn của một Int, vì vậy câu trả lời được báo cáo là không chính xác. Thay vào đó, danh sách tiếp theo cho thấy một cách để xử lý kết quả của các số ngẫu nhiên sao cho chúng nằm trong giới hạn hợp lý cho một bài kiểm tra tính toán.

Listing 11.10.
Generating suitable inputs for `quiz` (Arith.idr)

Safe division with the Divides view

Bạn có thể giảm một số nguyên tùy ý về giá trị giữa 1 và 12 bằng cách chia cho 12 và kiểm tra phần dư. Việc chia không phải lúc nào cũng an toàn, vì chia cho 0 là không xác định với Int, vì vậy bạn có thể sử dụng một cách nhìn về Int giải thích rằng một số là 0 hoặc được tạo thành từ một phép nhân cộng thêm một phần dư:

data Divides : Int -> (d : Int) -> Type where DivByZero : Int.Divides x 0 DivBy : (prf : rem >= 0 && rem < d = True) -> Int.Divides ((d * div) + rem) d divides : (val : Int) -> (d : Int) -> Divides val d

Lưu ý rằng trong trường hợp DivBy, bạn cũng có một chứng minh rằng số dư được đảm bảo có giá trị từ 0 đến số chia bằng cách sử dụng loại phương trình = được giới thiệu trong chương 8.

Bạn có thể sử dụng arithInputs như một nguồn đầu vào ngẫu nhiên cho bài kiểm tra và đảm bảo rằng tất cả các câu hỏi sẽ sử dụng các số từ 1 đến 12. Đây là một ví dụ:

*Arith> :exec quiz (arithInputs 12345) 0 Score so far: 0 2 * 1? 2 Correct! Score so far: 1 6 * 2? 18 Wrong, the answer is 12 Score so far: 1 11 * 10? 110 Correct! Score so far: 2

Bạn đã sử dụng thành công một nguồn số nguyên ngẫu nhiên làm đầu vào cho bài kiểm tra, và vì các số ngẫu nhiên (và do đó các arithInputs) tạo ra một chuỗi số vô hạn, bạn sẽ có thể tạo ra những số mới bao lâu tùy ý.

Tuy nhiên, còn một vấn đề còn lại, đó là bài kiểm tra tự nó không hoàn toàn:

*Arith> :total quiz Main.quiz is possibly not total due to recursive path: Main.quiz, Main.quiz

Điều này không thật sự nên làm bạn ngạc nhiên, vì không có gì trong định nghĩa của quiz cho phép nó kết thúc. Thay vào đó, giống như countFrom, randoms và arithInputs, nó đang đọc đầu vào của người dùng và liên tục sản xuất một chuỗi tác vụ IO vô hạn.

Trên thực tế, các chương trình tương tác thường có một vòng lặp bên ngoài, mà bạn có thể chạy vô hạn, gọi các lệnh cụ thể, mỗi lệnh mà bạn muốn kết thúc để có thể phát hành lệnh tiếp theo. Cách để viết các chương trình tương tác chạy vô hạn, do đó, là phân biệt giữa các loại chương trình tương tác mô tả các chuỗi hành động kết thúc (các lệnh trong vòng lặp chính của chúng ta) và các loại chương trình tương tác mô tả các chuỗi hành động có thể vô hạn (vòng lặp chính tự nó). Chúng ta sẽ khám phá điều này thêm trong phần tiếp theo.

Exercises

Write an every_other function that produces a new Stream from every second element of an input Stream. If you’ve implemented this correctly, you should see the following:
```
*ex_11_1> take 10 (every_other [1..]) [2, 4, 6, 8, 10, 12, 14, 16, 18, 20] : List Integer
```
Write an implementation of Functor (as described in section 7.3.1) for InfList. If you’ve implemented this correctly, you should see the following, using countFrom and getPrefix as defined in section 11.1.4:
```
*ex_11_1> getPrefix 10 (map (*2) (countFrom 1)) [2, 4, 6, 8, 10, 12, 14, 16, 18, 20] : List Integer
```
Define a Face data type that represents the faces of a coin: heads or tails. Then, define this:
```
coinFlips : (count : Nat) -> Stream Int -> List Face
```
This should return a sequence of count coin flips using the stream as a source of randomness. If you’ve implemented this correctly, you should see something like the following:
```
*ex_11_1> coinFlips 6 (randoms 12345) [Tails, Heads, Tails, Tails, Heads, Tails] : List Face
```
Hint: It will help to define a function, getFace : Int -> Face.
You can define a function to calculate the square root of a Double as follows:
1. Generate a sequence of closer approximations to the square root.
2. Take the first approximation that, when squared, is within a desired bound from the original number.
Write a function that generates a sequence of approximations:
```
square_root_approx : (number : Double) -> (approx : Double) -> Stream Double
```
Here, you’re looking for the square root of number, starting from an approximation, approx. You can generate the next approximation using this formula:
```
next = (approx + (number / approx)) / 2
```
If you’ve implemented this correctly, you should see the following:
```
*ex_11_1> take 3 (square_root_approx 10 10) [10.0, 5.5, 3.659090909090909] : List Double *ex_11_1> take 3 (square_root_approx 100 25) [25.0, 14.5, 10.698275862068964] : List Double
```
Write a function that finds the first approximation of a square root that’s within a desired bound, or within a maximum number of iterations:
```
square_root_bound : (max : Nat) -> (number : Double) -> (bound : Double) -> (approxs : Stream Double) -> Double
```
This should return the first element of approxs if max is zero. Otherwise, it should return the first element (let’s call it val) for which the difference between val x val and number is smaller than bound. If you’ve implemented this correctly, you should be able to define square_root as follows, and it should be total:
```
square_root : (number : Double) -> Double square_root number = square_root_bound 100 number 0.00000000001 (square_root_approx number number)
```
You can test it with the following values:
```
*ex_11_1> square_root 6 2.449489742783178 : Double *ex_11_1> square_root 2500 50.0 : Double *ex_11_1> square_root 2501 50.009999000199954 : Double
```

11.2. Infinite processes: writing interactive total programs

Khi bạn viết một hàm để tạo ra một Stream, bạn cung cấp một tiền tố của Stream và tạo ra phần còn lại một cách đệ quy. Điều này giống như quiz ở chỗ bạn cung cấp các hành động IO ban đầu để thực hiện và sau đó tạo ra phần còn lại của các hành động IO một cách đệ quy. Vì vậy, bạn có thể coi một chương trình tương tác như một chương trình tạo ra một chuỗi hành động tương tác tiềm năng vô hạn.

Trong chương 5, bạn đã viết các chương trình tương tác sử dụng loại tổng quát IO, trong đó IO ty là loại của các hành động tương tác kết thúc và trả về kết quả có loại ty. Trong phần này, bạn sẽ thấy cách viết các chương trình tương tác không kết thúc, nhưng hiệu quả (và do đó là tổng quát), bằng cách định nghĩa một loại InfIO để biểu diễn các chuỗi hành động IO vô hạn.

Bởi vì InfIO mô tả các chuỗi hành động vô hạn, các hàm phải có tính sản xuất, vì vậy bạn có thể chắc chắn rằng các chương trình kết quả tiếp tục tạo ra các hành động IO mới để thực thi trong khi tiếp tục chạy mãi mãi. Nhưng InfIO chỉ mô tả các chuỗi hành động tương tác, vì vậy bạn cũng cần viết một hàm để thực thi những hành động đó.

Tổng thể, chúng tôi sẽ áp dụng phương pháp sau để viết các chương trình tổng tương tác:

Define a type InfIO that describes infinite sequences of interactive actions.
Write nonterminating but productive functions using InfIO.
Define a run function that converts InfIO programs to IO actions.

Sự triển khai đầu tiên của bạn về run sẽ không hoàn chỉnh. Sau đó, bạn sẽ thấy cách tinh chỉnh định nghĩa để ngay cả run cũng hoàn chỉnh, bằng cách sử dụng một kiểu dữ liệu để mô tả thời gian mà việc thực thi nên tiếp tục. Tuy nhiên, trước tiên, bạn sẽ cần phải xem cách mô tả các quá trình vô hạn bằng cách định nghĩa InfIO.

11.2.1.
Describing infinite processes

Danh sách sau đây cho thấy cách định nghĩa loại InfIO. Nó tương tự như Stream, ngoại trừ việc, trong một chương trình tương tác, bạn có thể muốn giá trị được tạo ra từ hành động đầu tiên ảnh hưởng đến phần còn lại của một phép toán.

Listing 11.11.
Infinite interactive processes (InfIO.idr)

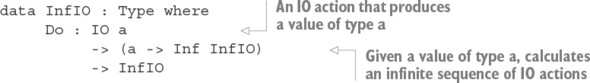
Có hai đối số cho Do:

A description of an IO action to execute
The remainder of the infinite sequence of actions. Because its type is a -> Inf InfIO, it can use the result produced by the first action to compute the remaining actions.

Bằng cách sử dụng Inf để đánh dấu phần còn lại của chuỗi là vô hạn, bạn đang nói với Idris rằng bạn mong đợi các hàm trả về giá trị có kiểu InfIO phải có tính sản xuất. Nói cách khác, cũng như với các hàm trên Stream, các gọi đệ quy bị chậm mà sinh ra một InfIO phải là các đối số cho một bộ tạo. Danh sách sau đây cho thấy cách điều này hoạt động trong một chương trình đệ quy mà liên tục hiển thị một thông điệp.

Listing 11.12.
An infinite process that repeatedly displays a message (InfIO.idr)

Cuộc gọi đệ quy đến loopPrint là một tham số cho hàm tạo Do, và loopPrint được đảm bảo sẽ tạo ra một hàm tạo (Do) như một tiền tố hữu hạn của kết quả của nó. Điều này đáp ứng định nghĩa của một hàm tổng quát có sản phẩm từ phần 11.1.3, vì vậy Idris hài lòng rằng loopPrint là tổng thể:

*InfIO> :total loopPrint Main.loopPrint is Total

Nhắc lại từ chương 5 rằng IO là một kiểu tổng quát mô tả các hành động tương tác và nó sẽ được thực thi bởi hệ thống runtime. Nếu bạn cố gắng đánh giá loopPrint tại REPL, bạn sẽ thấy một mô tả về hành động IO đầu tiên sẽ được thực thi và phần còn lại bị trì hoãn của chuỗi hành động vô hạn:

*InfIO> loopPrint "Hello" Do (io_bind (prim_write "Hello!\n") (\__bindx => io_return ())) (\underscore => Delay (loopPrint "Hello")) : InfIO

Cũng giống như với IO, để điều này trở nên hữu ích trong thực tế, bạn cũng cần có khả năng thực hiện các chuỗi hành động vô hạn.

11.2.2.
Executing infinite processes

Trong chương 5, bạn đã học cách mà hệ thống chạy Idris sẽ thực thi các chương trình có kiểu IO ty, trong đó ty là kiểu của giá trị được sản xuất bởi một phép tính tương tác. Vì vậy, để thực thi một giá trị có kiểu InfIO, bạn sẽ cần bắt đầu bằng cách chuyển nó thành IO (). Đây là một cách để thực hiện điều này.

Listing 11.13.
Converting an expression of type `InfIO` to an executable `IO` action (InfIO.idr)

Sử dụng run, bạn có thể chuyển đổi hàm của mình, hàm này in một thông điệp lặp lại, thành một hành động IO và thực thi nó bằng cách sử dụng :exec:

Bởi vì điều này chạy vô hạn, ít nhất cho đến khi bạn hủy nó bằng cách nhấn Ctrl-C, có lẽ bạn không nên ngạc nhiên khi thấy Idris không coi hàm run là tổng quát:

*InfIO> :total run Main.run is possibly not total due to recursive path: Main.run, Main.run

Bạn biết rằng loopPrint sẽ tiếp tục tạo ra các hành động IO mới để thực thi, vì nó là toàn phần. Điều này rất quý giá vì một chương trình tiếp tục thực hiện các hành động IO sẽ tiếp tục tiến triển một cách rõ ràng (ít nhất là giả sử rằng những hành động đó tạo ra một số đầu ra, điều mà chúng ta sẽ xem xét thêm trong phần 11.3.2). Sẽ thật tuyệt nếu run cũng là toàn phần, để bạn ít nhất biết rằng tất cả các hành động IO có thể xảy ra đều được xử lý và rằng không có bất kỳ sự không kết thúc không mong đợi nào do việc triển khai run gây ra.

Điều này có vẻ như là không thể: cách duy nhất để có một hàm tổng quát, không kết thúc là sử dụng kiểu Inf, và IO là một kiểu hành động kết thúc không sử dụng Inf. Thực tế, nếu bạn muốn các hàm thực thi vô hạn trong thời gian chạy, bạn sẽ cần ít nhất một cách nào đó để thoát ra khỏi các hàm tổng quát. Tuy nhiên, bạn có thể cố gắng làm cho việc thoát ra này càng yên lặng càng tốt.

Để đạt được điều này, chúng ta sẽ bắt đầu bằng cách tạo một phiên bản kết thúc của hàm chạy mà nhận làm tham số một giới hạn trên số lượng hành động mà nó sẵn sàng thực hiện.

11.2.3.
Executing infinite processes as total functions

Trước đó, trong phần 11.1.4, bạn đã viết một hàm getPrefix để lấy một phần hữu hạn của một danh sách vô hạn:

getPrefix : (count : Nat) -> InfList a -> List a

Bạn có thể nghĩ về tham số count như là “nhiên liệu” cho phép bạn tiếp tục xử lý danh sách vô hạn. Khi bạn hết nhiên liệu, bạn không thể xử lý thêm phần nào của danh sách nữa. Bạn có thể làm điều tương tự cho run, cung cấp cho nó một tham số bổ sung đại diện cho số lần lặp mà nó sẽ thực hiện.

Danh sách dưới đây định nghĩa một kiểu dữ liệu Nhiên liệu và đưa ra một định nghĩa hoàn toàn mới về chạy, cho phép thực hiện các hành động miễn là còn nhiên liệu.

Listing 11.14.
Converting an expression of type `InfIO` to an executable `IO` action running for a finite time (InfIO.idr)

Bây giờ, tổng số lượt chạy là:

*InfIO> :total run Main.run is Total

Thật không may, bạn vẫn gặp vấn đề vì bây giờ bạn cần chỉ định một số hành động tối đa rõ ràng mà chương trình được phép thực hiện, vì vậy bạn thực sự không còn các quy trình chạy vô thời hạn nữa! Ví dụ:

*InfIO> :exec run (tank 5) (loopPrint "vroom") vroom vroom vroom vroom vroom Out of fuel

Đảm bảo rằng việc thực thi hoàn toàn là rất quan trọng, vì nó đảm bảo rằng việc thực thi chính nó sẽ không gây ra bất kỳ sự không kết thúc nào ngoài ý muốn. Tuy nhiên, nếu bạn vẫn muốn các chương trình chạy vô hạn, bạn sẽ cần tìm cách tạo ra nhiên liệu một cách vô hạn. Bạn có thể đạt được điều này bằng cách sử dụng kiểu dữ liệu Lazy.

11.2.4.
Generating infinite structures using Lazy types

Nếu bạn có một phương thức để tạo ra Nhiên liệu vô hạn, bạn có thể chạy các chương trình tương tác mãi mãi. Danh sách 11.15 cho thấy cách bạn có thể làm điều này bằng cách sử dụng một hàm không tổng quát, mãi mãi. Bạn cũng cần thay đổi định nghĩa của Nhiên liệu để nó được rõ ràng trong kiểu rằng bạn chỉ tạo ra Nhiên liệu khi nó được yêu cầu.

Listing 11.15.
Generating infinite fuel (InfIO.idr)

forever and nontermination

Cần thiết để mãi mãi là không tổng quát vì nó (có chủ ý) đưa ra sự không kết thúc. May mắn thay, đây là chức năng không tổng quát duy nhất bạn cần để có thể thực thi các chương trình mãi mãi.

Mục đích của Lazy là để kiểm soát thời điểm Idris đánh giá một biểu thức. Như tên gọi Lazy ngụ ý, Idris sẽ không đánh giá một biểu thức có kiểu Lazy ty cho đến khi nó được yêu cầu một cách rõ ràng bởi Force, cái trả về một giá trị có kiểu ty. Prelude định nghĩa Lazy tương tự như Inf, mà bạn đã định nghĩa trong phần 11.1.2:

Lazy : Type -> Type Delay : (value : ty) -> Lazy ty Force : (computation : Lazy ty) -> ty

Ngoài ra, như Inf, Idris cũng chèn các cuộc gọi đến Delay và Force một cách ngầm định. Thực tế, Inf và Lazy đủ tương tự đến mức chúng được triển khai nội bộ bằng cách sử dụng cùng một kiểu cơ bản, như danh sách kế tiếp cho thấy. Sự khác biệt duy nhất trong thực tế giữa Inf và Lazy là cách mà bộ kiểm tra tính toàn vẹn xử lý chúng, như đã được giải thích trong phần bên.

Listing 11.16.
Internal definition of `Inf` and `Lazy`

Totality checking with Inf and Lazy

Tại thời điểm chạy, Inf và Lazy hoạt động giống nhau. Sự khác biệt chính giữa chúng là cách mà bộ kiểm tra tổng quát xử lý chúng. Idris phát hiện sự kết thúc bằng cách xem xét các tham số hội tụ về một trường hợp cơ sở, vì vậy nó cần phải biết liệu một tham số của một hàm tạo có nhỏ hơn (tức là gần hơn với một trường hợp cơ sở) so với biểu thức hàm tạo tổng thể hay không.

If the argument has type Lazy ty, for some type ty, it’s considered smaller than the constructor expression.
If the argument has type Inf ty, for some type ty, it’s not considered smaller than the constructor expression, because it may continue expanding indefinitely. Instead, Idris will check that the overall expression is productive, as discussed in section 11.1.3.

Nếu bạn sử dụng Inf cho Fuel, thay vì Lazy, chạy sẽ không còn tổng nữa vì đối số, fuel, sẽ không được coi là nhỏ hơn biểu thức More fuel.

Bạn đã triển khai ba hàm: loopPrint, là chương trình tương tác; run, thực thi các chương trình tương tác với lượng nhiên liệu cho trước; và forever, cung cấp một lượng nhiên liệu vô hạn. Tóm tắt:

loopPrint is a total function because it continues to produce IO actions indefinitely.
run is a total function because it will consume IO actions, executing them as long as there is Fuel available.
forever is a nontotal (or partial) function because it will never terminate and doesn’t produce any data inside an Inf type.

Bằng cách viết một phiên bản của hàm run để xử lý dữ liệu miễn là còn nhiên liệu, Idris có thể đảm bảo rằng hàm run là tổng quát, tiêu thụ nhiên liệu trong quá trình thực hiện. Bạn vẫn có một "cửa thoát" cho phép bạn chạy các chương trình tương tác vô thời hạn, dưới dạng hàm forever. Tuy nhiên, forever là hàm duy nhất không tổng quát.

Bạn vẫn có thể cải thiện định nghĩa của loopPrint chính nó. Khi chúng ta viết các chương trình tương tác ở chương 5, chúng ta đã sử dụng cú pháp do để giúp làm cho các chương trình tương tác dễ đọc hơn, nhưng chúng ta vẫn chưa thể làm điều đó bằng cách sử dụng InfIO. Tuy nhiên, bạn có thể mở rộng cú pháp do để hỗ trợ các kiểu dữ liệu của riêng bạn, như InfIO.

11.2.5.
Extending do notation for InfIO

Như bạn đã thấy trong chương 5, ký hiệu do được dịch sang các phép ứng dụng của toán tử (>>=), như lại được minh họa trong hình 11.3.

Figure 11.3.
Transforming `do` notation to an expression using the `>>=` operator when sequencing actions

Bạn đã thấy sự chuyển đổi này cho IO trong chương 5, cho Maybe trong chương 6, và nói chung cho các triển khai của giao diện Monad trong chương 7. Thực tế, sự chuyển đổi này là hoàn toàn cú pháp, vì vậy bạn có thể định nghĩa các triển khai riêng của (>>=) để sử dụng notations do cho các kiểu của riêng bạn. Danh sách dưới đây cho thấy cách bạn có thể định nghĩa notations do cho InfIO.

Listing 11.17.
Defining `do` notation for infinite sequences of actions

Idris dịch khối do thành các phép gọi của (>>=) và quyết định phiên bản nào của (>>=) để sử dụng bằng cách xem xét kiểu dữ liệu cần thiết. Ở đây, vì kiểu dữ liệu yêu cầu của biểu thức tổng thể là InfIO, nó sử dụng phiên bản của (>>=) tạo ra một giá trị có kiểu InfIO.

Loại InfIO cho phép bạn mô tả các chương trình tương tác chạy vô hạn, và bằng cách định nghĩa một toán tử (>>=), bạn có thể viết các chương trình đó giống như các chương trình với IO, với điều kiện rằng hành động cuối cùng là gọi một hàm có kiểu InfIO.

Bây giờ mà bạn đã thấy rằng bạn có thể viết các chương trình tương tác hiệu quả bằng cách sử dụng cú pháp do, chúng ta có thể xem lại bài kiểm tra toán học từ phần 11.1.6.

11.2.6.
A total arithmetic quiz

Để kết thúc phần này, chúng ta sẽ cập nhật bài kiểm tra toán học sao cho nó trở thành một hàm tổng quát, và bạn sẽ thấy cách bạn có thể tích hợp điều này vào một chương trình Idris hoàn chỉnh. Danh sách 11.18 cho thấy điểm khởi đầu của chúng ta, thiết lập loại InfIO và hàm chạy, như bạn đã thấy trước đó trong phần này. Bạn sẽ cần Data.Primitives.Views để tạo ra luồng số ngẫu nhiên. Bạn cũng sẽ nhập mô-đun Hệ thống để sử dụng hàm thời gian, mà bạn sẽ dùng để giúp khởi tạo luồng số ngẫu nhiên.

Listing 11.18.
Setting up `InfIO` (ArithTotal.idr)

The %default total directive

Idris hỗ trợ một số chỉ thị biên dịch thay đổi một số chi tiết về ngôn ngữ. Trong danh sách 11.18, chỉ thị %default total có nghĩa là Idris sẽ báo lỗi nếu có bất kỳ hàm nào mà nó không thể đảm bảo là toàn phần.

Bạn có thể ghi đè điều này cho từng hàm riêng lẻ bằng cách sử dụng từ khóa partial. Ví dụ, forever không phải là tổng quát:

partial forever : Fuel forever = More forever

Thật là một ý tưởng hay khi sử dụng %default total trong các chương trình của bạn, vì nếu Idris không thể xác định rằng một hàm là kết thúc hoặc có tính sản xuất, điều này có thể là dấu hiệu cho thấy có vấn đề với định nghĩa hàm. Hơn nữa, việc đánh dấu rõ ràng các hàm nào là hàm phần nghĩa là nếu có vấn đề với việc không kết thúc, hoặc một chương trình bị sập do thiếu đầu vào, bạn đã giảm thiểu số lượng hàm có thể gây ra vấn đề.

Danh sách 11.19 cho thấy bước tiếp theo, triển khai quiz bằng cách sử dụng InfIO. Bởi vì InfIO là một chuỗi vô hạn các hành động IO, bạn có thể viết quiz như trước, với bước cuối cùng là một cuộc gọi đệ quy. Thực tế, định nghĩa này giống hệt với định nghĩa trước; chỉ có loại đã thay đổi.

Listing 11.19.
Defining a total `quiz` function (ArithTotal.idr)

Bởi vì bạn đang sử dụng chú thích tổng số %default, bạn có thể chắc chắn rằng quiz là tổng số. Có hai cuộc gọi đệ quy tới quiz, và Idris có thể xác định rằng mỗi cuộc gọi đều được đảm bảo được nối tiếp bởi một chuỗi các hành động IO, vì vậy quiz được đảm bảo sẽ liên tục sản xuất các hành động IO vô thời hạn.

Bước cuối cùng là viết một hàm chính gọi hàm run để thực hiện quiz với một luồng các số nguyên. Dưới đây là các phần còn lại của việc triển khai.

Listing 11.20.
Completing the implementation with `main` (ArithTotal.idr)

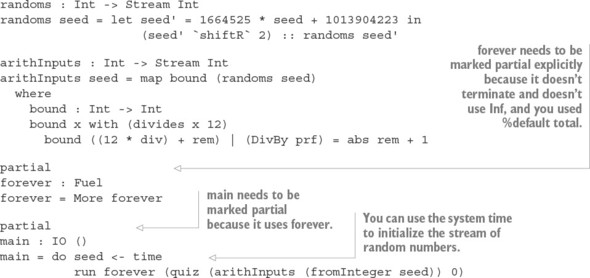
Bạn đã sử dụng randoms và arithInputs, như được định nghĩa trong phần 11.1.6, để tạo ra luồng các số nguyên. Bằng cách sử dụng thời gian hệ thống để khởi tạo luồng, bạn sẽ nhận được các câu hỏi khác nhau mỗi khi chạy chương trình.

Trong toàn bộ việc thực hiện, chỉ có hai hàm không phải là tổng quát là forever và main, cái sau chỉ vì nó cần sử dụng forever để tạo ra một lượng nhiên liệu không xác định cho run. Bởi vì bạn đã sử dụng chú thích %default total, bạn cần phải đánh dấu những hàm này là không tổng quát một cách rõ ràng. Điều đó có nghĩa là bạn có thể chắc chắn rằng nguyên nhân duy nhất có thể gây ra sự không hoàn thành trong chương trình là thực tế rằng bạn đã cố tình nói rằng chương trình nên chạy mãi mãi.

Ngoài mãi mãi, bạn biết rằng các thành phần riêng lẻ sẽ là một trong những điều sau đây:

Productive— Such as quiz continuing to produce IO actions for interpretation and randoms continuing to produce new random numbers when required
Terminating— Such as the individual IO commands and the generation of the next random number from a seed

Sự phân biệt này hữu ích cho việc viết các chương trình thực tế như máy chủ và REPL, mà bạn muốn chạy vô thời hạn trong khi chắc chắn rằng mỗi hành động riêng lẻ mà chương trình thực hiện đều kết thúc. Tuy nhiên, thường thì bạn sẽ muốn nhiều tính linh hoạt hơn. Hiện tại, chẳng hạn, bạn không có cách nào để thoát khỏi bài kiểm tra một cách sạch sẽ. Chúng ta sẽ quay lại vấn đề này trong phần tiếp theo.

Exercise

Hàm repl được định nghĩa trong Prelude không tổng quát vì nó là một hành động IO lặp vô hạn. Hãy triển khai một phiên bản mới của repl sử dụng InfIO:

totalREPL : (prompt : String) -> (action : String -> String) -> InfIO

Nếu bạn đã thực hiện điều này đúng cách, totalREPL nên bằng total, và bạn nên có thể thử nghiệm nó như sau:

*ex_11_2> :total totalREPL Main.totalREPL is Total *ex_11_2> :exec run forever (totalREPL "\n: " toUpper) : Hello [user input] HELLO : World [user input] WORLD

11.3. Interactive programs with termination

Sử dụng Inf, bạn có thể kiểm soát một cách rõ ràng khi nào bạn muốn dữ liệu được tạo ra, hoặc khi nào bạn muốn nó được tiêu thụ. Kết quả là, bạn có sự lựa chọn giữa các chương trình luôn kết thúc và các chương trình tiếp tục chạy mãi mãi. Tuy nhiên, để viết các ứng dụng hoàn chỉnh, bạn sẽ cần nhiều quyền kiểm soát hơn. Dù sao đi nữa, mặc dù bạn muốn một máy chủ hoạt động vô thời hạn, bạn vẫn muốn có khả năng tắt nó đi một cách gọn gàng khi bạn muốn.

Cho đến nay, các kiểu mà bạn đã định nghĩa bằng Inf chỉ có một constructor, do đó, chúng yêu cầu bạn tạo ra các chuỗi vô hạn. Thay vào đó, bạn có thể kết hợp các thành phần vô hạn và hữu hạn trong một kiểu dữ liệu duy nhất, điều này có nghĩa là bạn có thể mô tả các quá trình có thể chạy vô thời hạn, nhưng cũng được phép kết thúc. Trong phần này, bạn sẽ thấy cách làm tinh chỉnh kiểu InfIO để hỗ trợ các quá trình kết thúc một cách sạch sẽ. Hơn nữa, bạn sẽ thấy cách giới thiệu thêm độ chính xác vào kiểu, và định nghĩa một kiểu quá trình đặc biệt cho việc I/O trên console.

11.3.1.
Refining InfIO: introducing termination

Sử dụng InfIO, bạn có thể viết các chương trình tương tác hoàn toàn mà đảm bảo sẽ tiếp tục tạo ra các hành động IO, chạy mãi mãi. Danh sách sau đây cho thấy một ví dụ nhỏ của hình thức bạn đã thấy trong phần trước. Chương trình này yêu cầu người dùng nhập tên của họ và hiển thị lời chào.

Listing 11.21.
Repeatedly greeting a user, running forever (Greet.idr)

greet : InfIO greet = do putStr "Enter your name: " name <- getLine putStrLn ("Hello " ++ name) greet

Thông thường, khi bạn viết các chương trình tương tác, bạn sẽ muốn cung cấp một phương tiện để người dùng thoát. Không may, cách duy nhất mà một người dùng có thể thoát khỏi greet là bằng cách nhấn Ctrl-C. Không có cách nào để viết một hàm trong InfIO mà thoát theo cách khác!

Rất may, bạn có thể giải quyết điều này với một biến thể nhỏ trên InfIO. Kiểu Inf đánh dấu một giá trị là có thể vô hạn, thay vì đảm bảo rằng giá trị đó là vô hạn, và bạn có thể giới thiệu các nhà xây dựng dữ liệu bổ sung cho các kiểu có thể vô hạn. Bạn có thể định nghĩa một kiểu RunIO mới, như được hiển thị trong danh sách tiếp theo, thêm một nhà xây dựng Quit để mô tả các chương trình thoát, tạo ra một giá trị.

Listing 11.22.
The `RunIO` type, describing potentially infinite processes with an additional `Quit` command (RunIO.idr)

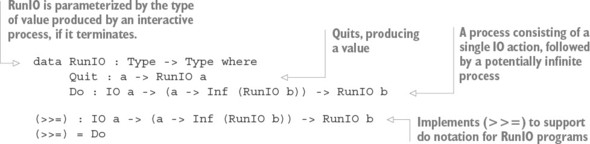
Sử dụng RunIO, bạn có thể viết một phiên bản của hàm greet, được hiển thị trong danh sách dưới đây, mà thoát khi người dùng nhập liệu rỗng.

Listing 11.23.
Repeatedly greets a user, exiting on empty input (RunIO.idr)

Tùy thuộc vào đầu vào, greet có thể hoặc là kết thúc hoặc là năng suất. Trình kiểm tra tính toàn vẹn chấp nhận greet là tổng quát, vì nó thỏa mãn định nghĩa từ phần 11.1.3 rằng một hàm tổng quát hoặc là kết thúc hoặc là năng suất cho tất cả các đầu vào có kiểu đúng.

Trước khi bạn có thể thực thi greet, bạn sẽ cần viết một phiên bản mới của run để chuyển đổi một chương trình trong RunIO thành một chuỗi hành động IO để hệ thống runtime thực thi. Trước đây, run chỉ kết thúc khi hết Fuel, nhưng bây giờ có hai lý do khả thi cho việc kết thúc:

Running out of Fuel, as before
Exiting cleanly, with a result, if the process being executed invokes Quit

Interactive programs and infinite types

Việc sử dụng một kiểu dữ liệu có thể vô hạn như RunIO không phải là điều độc đáo chỉ có ở Idris. Một ý tưởng tương tự đã được Peter Hancock và Anton Setzer mô tả trong bài báo năm 2004 của họ "Các chương trình tương tác và đồng trừ yếu trong lý thuyết loại phụ thuộc," tiếp nối từ công trình trước đó của họ trong việc mô tả các chương trình tương tác với các loại phụ thuộc.

Loại tổng quát Inf mà bạn sử dụng trong kiểu của các cấu trúc có thể vô hạn theo một ý tưởng tương tự được sử dụng trong ngôn ngữ lập trình Agda, được mô tả bởi Nils Anders Danielsson trong bài báo năm 2010 “Total Parser Combinators.”

Bạn có thể phân biệt những kết quả này theo loại:

run : Fuel -> RunIO a -> IO (Maybe a)

Các kết quả có thể của việc chạy tương ứng với hai lý do có thể cho việc kết thúc:

If run runs out of Fuel, it returns Nothing.
If run executes an action of the form Quit value, it returns Just value.

Danh sách dưới đây cung cấp định nghĩa mới của run cho RunIO.

Listing 11.24.
Converting an expression of type `RunIO ty` to an executable action of type `IO ty` (RunIO.idr)

Cuối cùng, bạn có thể viết một chương trình chính thực hiện hàm greet và bỏ qua kết quả.

partial main : IO () main = do run forever greet pure ()

Bởi vì hàm run hiện tạo ra một hành động IO mà khi gọi với greet thì sản sinh ra một giá trị có kiểu Maybe (), và main được kỳ vọng là tạo ra một hành động sản sinh ra giá trị có kiểu (), bạn cần kết thúc bằng cách gọi pure (). Khi bạn thực hiện main tại REPL, bây giờ bạn có thể thoát sạch sẽ bằng cách nhập một chuỗi rỗng:

Với RunIO, bạn đã tinh chỉnh InfIO với khả năng kết thúc một quy trình một cách gọn gàng khi cần thiết. Điều này mang lại cho bạn nhiều tự do hơn để viết các chương trình tương tác, nhưng còn một cách khác mà RunIO có thể nói là mang lại cho bạn quá nhiều tự do. Cụ thể, một quy trình được mô tả bởi RunIO là một chuỗi các hành động IO tùy ý, mang lại cho bạn nhiều khả năng, bao gồm các khả năng sau:

Reading from and writing to the console
Opening and closing files
Opening network connections
Deleting files

Đối với các chương trình bạn đã viết trong chương này, bạn chỉ quan tâm đến cái đầu tiên. Những cái còn lại không chỉ không cần thiết, mà còn dẫn đến khả năng xảy ra lỗ hổng bảo mật từ xa trong trường hợp thứ ba, và có thể gây ra lỗi hủy hoại trong trường hợp thứ tư.

Một trong những nguyên tắc của phát triển dựa trên kiểu, mà chúng ta đã thảo luận trong chương 1, là chúng ta nên cố gắng viết các kiểu mô tả chính xác nhất có thể các giá trị mà kiểu đó có thể chứa. Để kết thúc chương này, chúng ta sẽ xem xét cách chúng ta có thể tinh chỉnh kiểu RunIO để chỉ mô tả những hành động cần thiết để thực hiện bài kiểm tra toán học.

11.3.2.
Domain-specific commands

Bạn chỉ cần hai hành động IO khi triển khai bài kiểm tra toán: đọc từ và ghi vào bảng điều khiển. Thay vì cho phép các chương trình tương tác trong RunIO thực hiện các hành động ngẫu nhiên, do đó, bạn có thể hạn chế chúng chỉ còn những hành động mà bạn cần. Nghĩa là, bạn có thể ngăn chương trình của mình thực hiện bất kỳ hành động tương tác nào nằm ngoài phạm vi vấn đề mà bạn đang làm việc.

Danh sách tiếp theo hiển thị một loại ConsoleIO tinh chỉnh mô tả các chương trình tương tác chỉ hỗ trợ đọc từ và ghi vào bảng điều khiển.

Listing 11.25.
Interactive programs supporting only console I/O (ArithCmd.idr)

Hiệu quả, Command định nghĩa một giao diện tương tác mà các chương trình ConsoleIO có thể sử dụng. Bạn có thể nghĩ về nó như việc xác định các khả năng hoặc quyền hạn của các chương trình tương tác, loại bỏ bất kỳ hành động không cần thiết nào.

Bạn bây giờ cần phải tinh chỉnh việc thực hiện chạy để có thể thực thi các chương trình ConsoleIO.

Listing 11.26.
Executing a `ConsoleIO` program (ArithCmd.idr)

Domain-specific languages

Ngôn ngữ chuyên biệt cho miền (DSL) là một ngôn ngữ được chuyên biệt hóa cho một loại vấn đề cụ thể. Các DSL thường nhằm mục tiêu chỉ cung cấp những thao tác cần thiết khi làm việc trong một miền vấn đề cụ thể với một cách ký hiệu dễ tiếp cận cho các chuyên gia trong miền đó, trong khi loại bỏ bất kỳ thao tác nào thừa.

Theo một cách nào đó, ConsoleIO định nghĩa một DSL (Ngôn ngữ phân tầng miền) cho việc viết các chương trình console tương tác, vì nó giới hạn lập trình viên chỉ với các hành động tương tác cần thiết và loại bỏ những hành động không cần thiết như xử lý tệp hoặc giao tiếp mạng.

Danh sách 11.27 cho thấy cách bạn có thể điều chỉnh quiz để chạy dưới dạng chương trình ConsoleIO. Bằng cách nhìn vào kiểu quiz và các định nghĩa của ConsoleIO và run, bạn có thể đảm bảo rằng quiz chỉ thực hiện các hành động I/O trên console. Không có cách nào để nó mở hoặc đóng tệp, giao tiếp qua mạng, hoặc thực hiện bất kỳ hoạt động tương tác nào khác.

Listing 11.27.
The arithmetic quiz, written as a `ConsoleIO` program (ArithCmd.idr)

Để hoàn thành việc triển khai, bạn sẽ cần thực hiện một hàm chính. Danh sách sau đây cho thấy một triển khai mới của hàm chính thực hiện trò chơi trắc nghiệm và sau đó hiển thị điểm số cuối cùng của người chơi sau khi họ nhập lệnh thoát.

Listing 11.28.
A `main` function that executes the quiz and displays the final score (ArithCmd.idr)

Bạn vẫn có thể tinh chỉnh định nghĩa của bài kiểm tra một chút. Khi các hàm trở nên lớn hơn, việc chia chúng thành các hàm nhỏ hơn, mỗi hàm có vai trò rõ ràng, là một thực hành tốt. Ở đây, ví dụ, bạn có thể tách ra các hàm để báo cáo xem một câu trả lời là đúng hay sai, như trong danh sách dưới đây. Các hàm này phải tự mình là năng suất (kết thúc bằng cách gọi quiz, như họ làm ở đây) hoặc kết thúc nếu quiz vẫn được tổng quát.

Listing 11.29.
Lifting out components of `quiz` into separate functions (ArithCmd.idr)

Sau khi kiểm tra kiểu bài kiểm tra thành công, bạn có thể đưa ra một số đảm bảo về hành vi của nó bằng cách nhìn vào các kiểu và kiểm tra tính toàn bộ:

It will execute no interactive action other then putStr and getLine.
It will either exit immediately or execute at least one interactive action, because it is productive.
Every action executed will return a result in finite time, because it is total.

11.3.3.
Sequencing Commands with do notation

Trong việc thực hiện quiz, bạn đã sử dụng hai loại để xây dựng chức năng: Command và ConsoleIO:

Command describes single commands, which terminate.
ConsoleIO describes sequences of terminating commands, which might be infinite.

Vì vậy, bạn có thể có các lệnh đơn lẻ, hữu hạn, hoặc chuỗi các lệnh vô hạn. Nhưng cũng sẽ hữu ích nếu có thể xây dựng các lệnh tổng hợp; nghĩa là, các chuỗi lệnh được đảm bảo sẽ dừng lại. Ví dụ, bạn có thể muốn viết một lệnh tổng hợp hiển thị một lời nhắc và sau đó đọc và phân tích cú pháp đầu vào của người dùng. Danh sách tiếp theo cho thấy một kiểu đại diện cho các đầu vào có thể của người dùng, và một định nghĩa khung của một hàm để đọc và phân tích đầu vào.

Listing 11.30.
Defining a type for representing user input, and a composite command for reading and parsing input (ArithCmdDo.idr)

Để viết hàm này, bạn cần thực hiện các bước sau:

Display the prompt.
Read an input from the console.
Convert the input string to Input and return it.

Bởi vì Command hiện chỉ hỗ trợ các lệnh đơn, bạn sẽ cần mở rộng nó để hỗ trợ các chuỗi lệnh. Dưới đây là định nghĩa mở rộng, bao gồm hai bộ dữ liệu mới, Pure và Bind, và định nghĩa cập nhật tương ứng của runCommand.

Listing 11.31.
Extending `Command` to allow sequences of commands (ArithCmdDo.idr)

Bạn cũng có thể muốn định nghĩa (>>=) để hỗ trợ cú pháp do cho việc tuần tự hóa lệnh, nhưng định nghĩa sau đây không hoạt động như bạn mong đợi:

(>>=) : Command a -> (a -> Command b) -> Command b (>>=) = Bind

Nếu bạn thử điều này, Idris sẽ phàn nàn rằng (>>=) đã được định nghĩa, vì bạn đã định nghĩa cú pháp do cho ConsoleIO:

ArithCmdDo.idr:22:7:Main.>>= already defined

Idris cho phép định nghĩa nhiều hàm với cùng một tên, miễn là chúng ở các không gian tên khác nhau. Bạn đã thấy điều này với List và Vect, ví dụ, nơi mỗi loại có các hàm tạo gọi là Nil và (::) mà Idris phân biệt theo ngữ cảnh mà bạn sử dụng chúng.

Không gian tên được cung cấp bởi mô-đun nơi bạn định nghĩa các hàm. Các không gian tên cũng có tính phân cấp, vì vậy bạn có thể giới thiệu thêm các không gian tên bên trong một mô-đun. Bạn có thể có nhiều định nghĩa của các hàm được gọi (>>=) trong một mô-đun bằng cách giới thiệu các không gian tên mới cho mỗi hàm. Danh sách sau đây cho thấy cách bạn có thể định nghĩa các không gian tên mới cho mỗi (>>=).

Listing 11.32.
Creating two definitions of `(>>=)` in separate namespaces (ArithCmdDo.idr)

Nếu bạn kiểm tra loại của (>>=) tại REPL, bạn sẽ thấy tất cả các định nghĩa của (>>=) trong các không gian tên tương ứng của chúng, cùng với kiểu của chúng:

*ArithCmdDo> :t (>>=) Main.CommandDo.(>>=) : Command a -> (a -> Command b) -> Command b Main.ConsoleDo.(>>=) : Command a -> (a -> Inf (ConsoleIO b)) -> ConsoleIO b Prelude.Monad.(>>=) : Monad m => m a -> (a -> m b) -> m b

Defining a Monad implementation for Command

Bạn cũng có thể định nghĩa một cài đặt của giao diện Monad cho Command, như đã mô tả trong chương 7. Khi có thể, điều này thường được ưa thích hơn vì các thư viện Prelude và base định nghĩa nhiều hàm làm việc một cách tổng quát với các cài đặt Monad. Để làm điều này, bạn cũng cần định nghĩa các cài đặt của Functor và Applicative. Bạn sẽ thấy một ví dụ về cách thực hiện điều này cho một loại tương tự trong chương tiếp theo.

Tuy nhiên, bạn không thể định nghĩa một triển khai của Monad cho ConsoleIO, vì kiểu của ConsoleDo.(>>=) không phù hợp với kiểu của phương thức (>>=) trong giao diện Monad.

Sử dụng CommandDo.(>>=) để cung cấp cú pháp do, bạn có thể hoàn thành định nghĩa của readInput.

Listing 11.33.
Implementing `readInput` by sequence `Command` (ArithCmdDo.idr)

readInput : (prompt : String) -> Command Input readInput prompt = do PutStr prompt answer <- GetLine if toLower answer == "quit" then Pure QuitCmd else Pure (Answer (cast answer))

Cuối cùng, bạn có thể sử dụng readInput trong hàm quiz chính để bao bọc các chi tiết về việc hiển thị yêu cầu và phân tích đầu vào của người dùng, như được thể hiện trong định nghĩa cuối cùng.

Listing 11.34.
Defining `quiz` using `readInput` as a composite command to display a prompt and read user input (ArithCmdDo.idr)

Trong định nghĩa cuối cùng này, bạn phân biệt giữa các chuỗi lệnh kết thúc (sử dụng Command) và các chương trình nhập/xuất console có thể không kết thúc (sử dụng ConsoleIO). Về mặt cú pháp, bạn viết các hàm theo cùng một cách trong mỗi loại, nhưng kiểu dữ liệu cho bạn biết liệu hàm đó có được phép chạy vô hạn hay không, hoặc liệu nó phải kết thúc cuối cùng.

Exercises

Update quiz so that it keeps track of the total number of questions and then returns the number of correct answers and the number of questions attempted. A sample run might look something like this:

*ex_11_3> :exec Score so far: 0 / 0 9 * 11? 99 Correct! Score so far: 1 / 1 6 * 9? 42 Wrong, the answer is 54 Score so far: 1 / 2 10 * 2? 20 Correct! Score so far: 2 / 3 7 * 2? quit Final score: 2 / 3

Extend the Command type from section 11.3.2 so that it also supports reading and writing files. Hint: Look at the types of readFile and writeFile in the Prelude to decide what types your data constructors should have.
Use your extended Command type to implement an interactive “shell” that supports the following commands:
- cat [filename], which reads a file and displays its contents
- copy [source] [destination], which reads a source file and writes its contents to a destination file
- exit, which exits the shell

11.4. Summary

You can generate infinite data using Inf to state which parts of a structure are potentially infinite.
A total function either terminates with a well-typed input or produces a prefix of a well-typed infinite result in finite time.
You can process infinite structures by using finite data to determine how much of the infinite structure to use.
The Prelude defines a Stream data type for constructing infinite lists.
You can define processes as infinite sequences of IO actions.
To execute an infinite process, you define a function that takes an argument stating how long the process should run.
The partial function forever allows processes to run indefinitely by generating an infinite amount of Fuel, using the Lazy type.
By implementing (>>=), you can extend do notation for your own data types to make programs easier to read and write.
You can mix finite and infinite structures within the same data type to define potentially infinite processes that may also terminate.

Chapter 12.
Writing programs with state

Chương này đề cập đến

Using the State type to describe mutable state
Implementing custom types for state management
Defining and using records for global system state

Idris là một ngôn ngữ thuần túy, vì vậy các biến là bất biến. Khi một biến được định nghĩa với một giá trị, không có gì có thể cập nhật nó. Điều này có thể gợi ý rằng việc viết các chương trình thao tác trạng thái là khó khăn, hoặc thậm chí là không thể, hoặc rằng các lập trình viên Idris nói chung không quan tâm đến trạng thái. Trong thực tế, điều ngược lại là đúng.

Trong phát triển dựa trên kiểu, kiểu của một hàm cho bạn biết chính xác hàm đó có thể làm gì về mặt đầu vào và đầu ra được cho phép. Vì vậy, nếu bạn muốn viết một hàm thao tác trạng thái, bạn có thể làm điều đó, nhưng bạn cần phải rõ ràng về điều đó trong kiểu của hàm. Thực tế, chúng ta đã làm điều này trong các chương trước:

In chapter 4, we implemented an interactive data store using global state.
In chapter 9, we implemented a word-guessing game using global state to hold the target word, the letters guessed, and the number of guesses still available.
In chapter 11, we implemented an arithmetic game using global state to hold the user’s current score.

Trong mỗi trường hợp, chúng tôi đã triển khai trạng thái bằng cách viết một hàm đệ quy mà nhận trạng thái hiện tại của toàn bộ chương trình làm đối số.

Hầu hết các ứng dụng thực tế đều cần thao tác với trạng thái ở một mức độ nhất định. Đôi khi, như trong các ví dụ trước, trạng thái là toàn cục và được sử dụng xuyên suốt ứng dụng. Đôi khi, trạng thái chỉ thuộc về một thuật toán; ví dụ, một thuật toán duyệt đồ thị sẽ giữ các nút mà nó đã truy cập trong trạng thái cục bộ để tránh truy cập các nút nhiều hơn một lần. Trong chương này, chúng ta sẽ xem xét cách quản lý trạng thái có thể thay đổi trong Idris, cả cho trạng thái cục bộ thuộc về một thuật toán, và cho việc đại diện cho trạng thái tổng thể của hệ thống.

State management and dependent types

Chúng tôi sẽ không sử dụng nhiều kiểu phụ thuộc trong chương này; việc sử dụng kiểu phụ thuộc trong trạng thái tạo ra một số phức tạp, cũng như cơ hội để chính xác hơn trong việc mô tả các hệ thống chuyển đổi trạng thái và các giao thức. Chúng ta sẽ xem xét những cơ hội này trong hai chương tiếp theo, nhưng chúng ta sẽ bắt đầu ở đây bằng cách tìm hiểu cách thức hoạt động của trạng thái nói chung.

Trước đây, chúng tôi đã sử dụng kiểu để mô tả các chương trình tương tác theo các chuỗi lệnh, sử dụng IO trong chương 5 và ConsoleIO trong chương 11. Các chương trình có trạng thái có thể hoạt động theo cách tương tự, sử dụng kiểu để mô tả các hoạt động mà một chương trình có trạng thái có thể thực hiện. Chúng ta sẽ bắt đầu bằng việc xem xét kiểu State tổng quát được định nghĩa trong thư viện Idris và sau đó là cách chúng ta có thể tự định nghĩa các kiểu như State. Cuối cùng, chúng ta sẽ xem cách chúng ta có thể cấu trúc một ứng dụng hoàn chỉnh với trạng thái, tinh chỉnh bài kiểm tra toán học từ chương 11.

12.1. Working with mutable state

Dù Idris là một ngôn ngữ thuần túy, nhưng thường thì việc làm việc với trạng thái lại rất hữu ích. Đặc biệt, khi viết các hàm với cấu trúc dữ liệu phức tạp, chẳng hạn như cây hoặc đồ thị, việc có thể đọc và ghi trạng thái cục bộ khi bạn đang duyệt qua cấu trúc đó là rất hữu ích. Trong phần này, bạn sẽ thấy cách quản lý trạng thái có thể thay đổi.

Comparing state in Idris and Haskell

Phần này mô tả kiểu State để nắm bắt trạng thái có thể thay đổi tại địa phương trong Idris. Nếu bạn quen thuộc với Haskell, bạn sẽ thấy rằng bạn có thể sử dụng State trong Idris theo cùng một cách như Haskell, bằng cách nhập Control.Monad.State. Nếu bạn quen thuộc với kiểu State trong Haskell, bạn có thể tiếp tục an toàn đến phần 12.2, nơi tôi sẽ mô tả một triển khai tùy chỉnh của State.

Trong chương trước, bạn đã viết một hàm để gán nhãn cho các phần tử của một danh sách, lấy nhãn từ một Stream. Nó được lặp lại ở đây để tham khảo.

Listing 12.1.
Labeling each element of a `List` using a `Stream` (Streams.idr)

Trong phần này, bạn sẽ triển khai một hàm tương tự để gán nhãn cho một cây nhị phân. Đầu tiên, bạn sẽ thấy cách thực hiện trạng thái có thể thay đổi bằng tay, với mỗi hàm trả về một cặp lưu trữ trạng thái đã được cập nhật cùng với kết quả của một phép toán. Sau đó, bạn sẽ thấy cách bao bọc trạng thái bằng một kiểu State được định nghĩa trong thư viện cơ sở của Idris. Trước tiên, tôi sẽ mô tả ví dụ về việc duyệt cây một cách chi tiết hơn.

12.1.1.
The tree-traversal example

Hình 12.1 cho thấy kết quả của một hàm gán nhãn cho một cây nhị phân, và chúng tôi sẽ sử dụng điều này như một ví dụ xuyên suốt phần này. Hàm này gán nhãn cho các nút theo thứ tự sâu trước, từ trái sang phải, vì vậy nút bên trái sâu nhất nhận nhãn đầu tiên, và nút bên phải sâu nhất nhận nhãn cuối cùng.

Figure 12.1.
Labeling a tree, depth first. Each node is labeled with an integer.

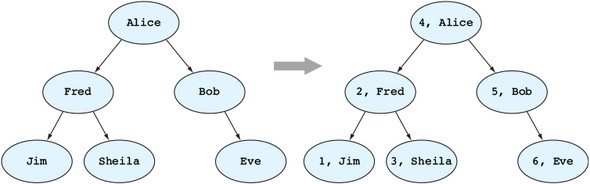
Danh sách dưới đây cung cấp định nghĩa của các cây nhị phân mà chúng ta sẽ sử dụng để gán nhãn, cùng với testTree, một biểu diễn của cây cụ thể mà chúng ta sẽ gán nhãn (từ ví dụ trong hình 12.1).

Listing 12.2.
Definition of binary trees, and an example (TreeLabel.idr)

Thuận tiện để định nghĩa flatten sao cho bạn có thể dễ dàng thấy được thứ tự mà các nhãn nên được áp dụng:

*TreeLabel> flatten testTree ["Jim", "Fred", "Sheila", "Alice", "Bob", "Eve"] : List String

Khi bạn đã viết một hàm treeLabel để gán nhãn cho các nút trong cây dựa trên các phần tử trong một luồng, bạn nên có khả năng chạy nó như sau:

*TreeLabel> flatten (treeLabel testTree) [(1, "Jim"), (2, "Fred"), (3, "Sheila"), (4, "Alice"), (5, "Bob"), (6, "Eve")] : List (Integer, String)

Khi bạn viết hàm gán nhãn cho danh sách trong danh sách 12.1, bạn đã có một sự tương ứng trực tiếp giữa cấu trúc của dòng nhãn và danh sách mà bạn đang gán nhãn. Cụ thể, với mỗi (::) trong danh sách, bạn có thể lấy phần tử đầu tiên của dòng làm nhãn, và sau đó đệ quy gán nhãn cho phần còn lại của danh sách. Với cây, điều này phức tạp hơn một chút, vì khi bạn gán nhãn cho cây con bên trái, bạn không biết trước mình sẽ cần lấy bao nhiêu phần tử từ dòng. Hình 12.2 minh họa việc gán nhãn cho các cây con trong ví dụ này.

Figure 12.2.
Labeling subtrees. The left subtree is labeled from `1` to `3`, and the right subtree is labeled from `5` to `6`.

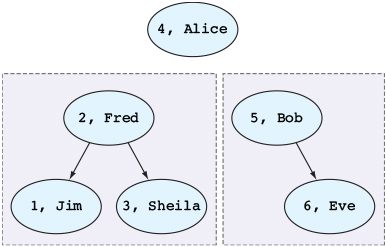
Trước khi gán nhãn cho cây con bên phải, bạn cần biết có bao nhiêu phần tử bạn đã lấy từ dòng khi gán nhãn cho cây con bên trái. Không chỉ hàm gán nhãn cần phải trả về cây đã được gán nhãn, nó cũng cần phải trả về một số thông tin về nơi bắt đầu gán nhãn cho phần còn lại của cây.

Một cách tự nhiên để thực hiện điều này có thể là cho hàm gán nhãn nhận dòng nhãn làm đầu vào, như trước, và trả về một cặp, chứa

The labeled tree
A new stream of labels that you can use to label the rest of the tree

Chúng ta sẽ bắt đầu bằng cách triển khai nhãn cây theo cách này, sử dụng một cặp để đại diện cho kết quả của phép toán và trạng thái của các nhãn. Sau đó, bạn sẽ thấy cách kiểu State được định nghĩa trong thư viện Idris bao encapsulate các chi tiết quản lý trạng thái trong loại thuật toán này.

12.1.2.
Representing mutable state using a pair

Danh sách 12.3 định nghĩa một hàm trợ giúp để gán nhãn cho một cây bằng một chuỗi nhãn, và sử dụng một cặp để đại diện cho trạng thái của chuỗi sau khi mỗi cây con được gán nhãn. Hàm trợ giúp trả về phần chưa sử dụng của chuỗi nhãn, để khi bạn đã gán nhãn cho một cây con, bạn biết bắt đầu gán nhãn cho cây con tiếp theo từ đâu.

Listing 12.3.
Labeling a `Tree` with a stream of labels (TreeLabel.idr)

Nếu bạn thử gán nhãn cho cây ví dụ, bạn sẽ thấy rằng các nhãn được áp dụng theo thứ tự bạn mong đợi:

*TreeLabel> flatten (treeLabel testTree) [(1, "Jim"), (2, "Fred"), (3, "Sheila"), (4, "Alice"), (5, "Bob"), (6, "Eve")] : List (Integer, String)

Bạn có thể kiểm tra rằng việc gán nhãn cũng bảo tồn cấu trúc của cây bằng cách bỏ qua cuộc gọi đến flatten:

*TreeLabel> treeLabel testTree Node (Node (Node Empty (1, "Jim") Empty) (2, "Fred") (Node Empty (3, "Sheila") Empty)) (4, "Alice") (Node Empty (5, "Bob") (Node Empty (6, "Eve") Empty)) : Tree (Integer, String)

Trong định nghĩa hiện tại của treeLabelWith, bạn cần theo dõi trạng thái của luồng nhãn. Gán nhãn cho một cây con không chỉ mang lại cho bạn một cây với các nhãn gắn liền với các nút, mà còn cung cấp cho bạn một luồng nhãn mới để gán nhãn cho phần tiếp theo của cây.

Khi bạn duyệt cây, bạn giữ theo dõi trạng thái của dòng bằng cách truyền nó như một tham số và trả về trạng thái đã cập nhật. Về cơ bản, hàm sử dụng trạng thái có thể thay đổi tại chỗ, với trạng thái được gửi qua định nghĩa một cách rõ ràng. Mặc dù điều này hoạt động, nhưng có hai vấn đề với cách tiếp cận này:

It’s error-prone because you need to ensure that the correct state is propagated correctly to the recursive calls. Notice that left_labelled and right_labelled have the same type, for example, so it’s easy to use the wrong one!
It’s hard to read because the details of the algorithm are hidden behind the details of state management.

Thường thì việc có trạng thái thay đổi cục bộ là rất hữu ích, và giống như bất kỳ khái niệm nào bạn sử dụng thường xuyên, tốt nhất là tạo ra một sự trừu tượng để nắm bắt khái niệm đó. Bạn có thể cải thiện định nghĩa của treeLabel, làm cho nó ít bị lỗi hơn và dễ đọc hơn, bằng cách sử dụng một kiểu dữ liệu nắm bắt rõ ràng khái niệm trạng thái.

12.1.3.
State, a type for describing stateful operations

Lý do duy nhất bạn truyền dòng nhãn xung quanh trong định nghĩa của treeLabelWith là khi bạn gặp một giá trị tại một nút, bạn cần liên kết nó với một giá trị nhãn. Trong một ngôn ngữ mệnh lệnh, bạn có thể truyền một biến có thể thay đổi cho treeLabelWith và cập nhật nó khi bạn gặp từng nút. Bởi vì Idris là một ngôn ngữ hoàn toàn hàm, bạn không có các biến có thể thay đổi, nhưng thư viện cơ sở cung cấp một kiểu để mô tả các chuỗi thao tác trạng thái, trong module Control.Monad.State. Control.Monad.State xuất khẩu các định nghĩa liên quan sau đây.

Listing 12.4.
`State` and associated functions, defined in `Control.Monad.State`

Giống như một giá trị của kiểu IO ty mô tả một chuỗi các thao tác tương tác tạo ra một giá trị của kiểu ty, một giá trị của kiểu State Nat ty mô tả một chuỗi các thao tác đọc và ghi một trạng thái có thể thay đổi của kiểu Nat. Danh sách 12.5 cung cấp một ví dụ nhỏ về một hàm hoạt động với trạng thái có thể thay đổi. Nó đọc trạng thái bằng cách sử dụng get và sau đó cập nhật nó bằng cách sử dụng put, làm tăng trạng thái Nat theo giá trị đã cho.

Listing 12.5.
A stateful function that increases a state by a given value (State.idr)

Một giá trị có kiểu State Nat () là một mô tả về các hoạt động có trạng thái sử dụng một trạng thái có kiểu Nat. Bạn có thể thực hiện nó bằng cách sử dụng runState bằng cách truyền cho nó các hoạt động và một trạng thái ban đầu. Ví dụ, bạn có thể thực hiện tăng 5 với trạng thái ban đầu là 89:

*State> runState (increase 5) 89 ((), 94) : ((), Nat)

Kết quả là một cặp giá trị được tạo ra bởi các phép toán có trạng thái, trong trường hợp này là giá trị đơn vị (), và trạng thái cuối cùng, trong trường hợp này là 94. Cũng có hai biến thể của runState:

evalState—Returns only the value produced by the sequence of operations:

*State> :t evalState evalState : State stateType a -> stateType -> a *State> evalState (increase 5) 89 () : ()

execState—Returns only the final state after the sequence of operations:

*State> :t execState execState : State stateType a -> stateType -> stateType *State> execState (increase 5) 89 94 : Nat

Generic types of State

Nếu bạn kiểm tra các kiểu của get và put, bạn sẽ thấy rằng chúng sử dụng các kiểu tổng quát có ràng buộc:

*TreeLabelState> :t get get : MonadState stateType m => m stateType *TreeLabelState> :t put put : MonadState stateType m => stateType -> m ()

Điều này mang lại cho các tác giả thư viện nhiều sự linh hoạt hơn trong việc định nghĩa các chương trình có trạng thái. Chi tiết của giao diện MonadState nằm ngoài phạm vi của cuốn sách này, nhưng bạn có thể đọc thêm trong tài liệu thư viện Idris (http://idris-lang.org/documentation). Trong ví dụ này, bạn có thể đọc m như State stateType.

Mặc dù State bao encapsulates các chuỗi thao tác có trạng thái, nhưng bên trong nó được định nghĩa bằng các hàm thuần túy. Về cơ bản, nó đóng gói mẫu cài đặt mà bạn đã sử dụng để truyền trạng thái xung quanh trong treeLabelWith.

Sử dụng State, bạn có thể tái triển khai treeLabelWith, ẩn đi các chi tiết nội bộ của việc quản lý trạng thái và chỉ đọc cũng như cập nhật luồng nhãn khi cần thiết.

12.1.4.
Tree traversal with State

Danh sách tiếp theo cho thấy cách bạn có thể định nghĩa treeLabelWith bằng cách giữ lại luồng nhãn như một trạng thái, đọc nó để lấy nhãn tiếp theo cho một nút.

Listing 12.6.
Defining `treeLabelWith` as a sequence of stateful operations (TreeLabelState.idr)

Trong định nghĩa này, bạn có thể thấy các chi tiết của thuật toán gán nhãn rõ ràng hơn so với định nghĩa trước. Ở đây, bạn để lại các chi tiết nội bộ của việc quản lý trạng thái cho việc triển khai của State.

Để chạy chức năng này và thực hiện việc dán nhãn cây, bạn cần cung cấp một trạng thái ban đầu. Dưới đây là danh sách định nghĩa một hàm treeLabel, mà khởi tạo trạng thái với một dòng chảy vô tận các số nguyên, đếm lên từ 1.

Listing 12.7.
Top-level function to label tree nodes, depth first, left to right (TreeLabelState.idr)

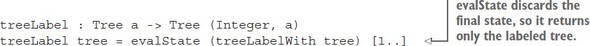
Như trước đây, bạn có thể kiểm tra điều này tại REPL. Nó hoạt động giống như cách triển khai trước đó của treeLabel trên dữ liệu kiểm tra:

*TreeLabelState> flatten (treeLabel testTree) [(1, "Jim"), (2, "Fred"), (3, "Sheila"), (4, "Alice"), (5, "Bob"), (6, "Eve")] : List (Integer, String)

Giống như IO, mà bạn lần đầu gặp trong chương 5, State cung cấp cho bạn một cách viết các hàm có tác dụng phụ (ở đây, là thay đổi trạng thái có thể thay đổi) bằng cách mô tả chuỗi các hoạt động và thực thi chúng một cách riêng biệt:

A value of type IO ty is a description of a sequence of interactive actions producing a result of type ty. It’s executed by the runtime system by compilation, or by :exec at the REPL.
A value of type State stateType ty is a description of a sequence of actions that read and write a state of type stateType, producing a result of type ty. It’s executed by using one of runState, execState, or evalState.

Nhiều chương trình thú vị tuân theo mẫu này, định nghĩa một kiểu để mô tả chuỗi các lệnh và một hàm riêng biệt để thực thi những lệnh đó. Thực vậy, bạn đã thấy một ví dụ trong chương 11, khi bạn định nghĩa kiểu ConsoleIO để mô tả các chương trình tương tác chạy không giới hạn. Bạn sẽ thấy nhiều ví dụ hơn trong các chương còn lại, vì vậy trong phần còn lại của chương này, chúng ta sẽ xem xét cách thực hiện các kiểu tùy chỉnh để đại diện cho trạng thái và sự tương tác.

Exercises

Write a function that updates a state by applying a function to the current state:
```
update : (stateType -> stateType) -> State stateType ()
```
You should be able to use update to reimplement increase:
```
increase : Nat -> State Nat () increase x = update (+x)
```
You can test your answer at the REPL as follows:
```
*ex_12_1> runState (increase 5) 89 ((), 94) : ((), Nat)
```
Write a function that uses State to count the number of occurrences of Empty in a tree. It should have the following type:
```
countEmpty : Tree a -> State Nat ()
```
You can test your answer at the REPL with testTree as follows:
```
*ex_12_1> execState (countEmpty testTree) 0 7 : Nat
```
Write a function that counts the number of occurrences of both Empty and Node in a tree, using State to store the count of each in a pair. It should have the following type:
```
countEmptyNode : Tree a -> State (Nat, Nat) ()
```
You can test your answer at the REPL with testTree as follows:
```
*ex_12_1> execState (countEmptyNode testTree) (0, 0) (7, 6) : (Nat, Nat)
```

12.2. A custom implementation of State

Trong phần trước, bạn đã thấy rằng kiểu State cung cấp cho bạn một cách tổng quát để triển khai các thuật toán sử dụng trạng thái. Bạn đã sử dụng nó để duy trì một dòng nhãn như trạng thái có thể thay đổi cục bộ, mà bạn có thể truy cập bằng cách đọc (sử dụng get) và ghi (sử dụng put) khi cần thiết. Giống như IO, tách biệt mô tả của một chương trình tương tác ra khỏi việc thực thi của nó tại thời điểm chạy, State tách biệt mô tả của một chương trình có trạng thái ra khỏi việc thực thi với một trạng thái cụ thể.

Chúng ta sẽ xem thêm nhiều ví dụ về cùng một mẫu, tách biệt phần mô tả một chương trình khỏi việc thực thi của nó, trong các chương còn lại, vì vậy trước khi tiếp tục, hãy cùng khám phá cách chúng ta có thể tự định nghĩa kiểu State, cùng với runState để thực hiện các phép toán có trạng thái. Trong phần này, bạn sẽ thấy một cách để định nghĩa State, và cách cung cấp các cài đặt cho một số giao diện của State: Functor, Applicative và Monad. Bằng cách triển khai các giao diện này, bạn sẽ có thể sử dụng một số hàm thư viện tổng quát với State.

12.2.1.
Defining State and runState

Danh sách sau đây cho thấy một cách bạn có thể định nghĩa State bằng tay, với một bộ dữ liệu Get để mô tả thao tác đọc trạng thái và một bộ dữ liệu Put để mô tả thao tác ghi trạng thái.

Listing 12.8.
A type for describing stateful operations (TreeLabelType.idr)

Naming conventions reminder

Hãy nhớ rằng, theo quy ước, tên loại và tên bộ dựng dữ liệu trong Idris bắt đầu bằng chữ cái in hoa. Tôi sẽ không đi lệch khỏi quy ước này ở đây, vì vậy nếu bạn muốn những tên giống như những tên được xuất bởi Control.Monad.State, bạn sẽ cần phải định nghĩa các hàm sau:

get : State stateType stateType get = Get put : stateType -> State stateType () put = Put pure : ty -> State stateType ty pure = Pure

Bạn có thể hỗ trợ cú pháp do cho State bằng cách định nghĩa (>>=). Bạn có thể thực hiện điều này bằng cách hiện thực hóa giao diện Monad cho (>>=), hoặc bằng cách định nghĩa (>>=) trực tiếp:

(>>=) : State stateType a -> (a -> State stateType b) -> State stateType b (>>=) = Bind

Implementing interfaces for State

Định nghĩa (>>=) có nghĩa là bạn có thể sử dụng cú pháp do cho các chương trình trong State. Như bạn đã thấy ở chương 7, (>>=) cũng là một phương thức của giao diện Monad, mà cũng yêu cầu các triển khai của giao diện Functor và Applicative. Nó được định nghĩa ở đây như một hàm độc lập để tránh cần phải triển khai Functor và Applicative trước cho ví dụ này.

Khi có thể, việc triển khai giao diện Monad là một ý tưởng rất tốt, vì điều đó giúp bạn truy cập vào một số hàm tổng quát hạn chế được định nghĩa bởi thư viện Idris. Chẳng hạn, bạn sẽ có thể sử dụng hàm when, hàm thực hiện một thao tác khi một điều kiện được thỏa mãn, và hàm traverse, hàm áp dụng một phép toán qua một cấu trúc. Bạn sẽ thấy cách thực hiện điều này cho State trong phần 12.2.2.

Sử dụng phiên bản này của State, và định nghĩa các hàm get, put và pure, mà trực tiếp sử dụng các bộ dữ liệu, danh sách 12.9 cho thấy cách bạn có thể định nghĩa treeLabelWith. Phiên bản này hoàn toàn giống với phiên bản trước đó, như bạn mong đợi, vì nó sử dụng cùng tên cho các hàm thao tác với trạng thái.

Listing 12.9.
Defining `treeLabelWith` as a sequence of stateful operations (TreeLabelType.idr)

Để chạy nó, bạn cần định nghĩa một hàm chuyển đổi mô tả của các thao tác trạng thái thành hàm gán nhãn cây. Danh sách sau đây cho thấy định nghĩa của runState, hàm nhận một mô tả của một chương trình có trạng thái và một trạng thái ban đầu, và trả về giá trị được chương trình có trạng thái tạo ra cùng với trạng thái cuối cùng.

Listing 12.10.
Running a labeling operation (TreeLabelType.idr)

Khi bạn chạy các chuỗi thao tác có trạng thái, được định nghĩa bằng cách sử dụng Bind, bạn cần lấy trạng thái nextState được trả về khi chạy cmd và truyền nó cho runState khi thực hiện phần còn lại của các thao tác. Bạn tính toán phần còn lại của các thao tác bằng cách lấy giá trị val được trả về khi chạy cmd và truyền nó cho prog. Điều này đóng gói quản lý trạng thái mà bạn đã phải triển khai bằng tay (ba lần!) trong triển khai đầu tiên của bạn cho treeLabelWith, và nó tương tự như cách mà mô-đun Control.Monad.State thực hiện State tự nó.

Danh sách dưới đây cho thấy định nghĩa của treeLabel sử dụng việc triển khai mới của treeLabelWith, khởi tạo luồng với [1..].

Listing 12.11.
The tree-labeling function, which calls `run` with an initial stream of labels (TreeLabelType.idr)

12.2.2.
Defining Functor, Applicative, and Monad implementations for State

Việc triển khai (>>=) cho State có nghĩa là bạn có thể sử dụng cú pháp do, điều này cung cấp một cú pháp rõ ràng, dễ đọc để viết các hàm mô tả chuỗi các thao tác. Nhưng cú pháp do chỉ cung cấp cho chúng ta điều đó.

Thay vì định nghĩa (>>=) như một hàm độc lập, việc triển khai các giao diện Functor, Applicative và Monad cho State là một ý tưởng hay. Ngoài việc cung cấp cú pháp do thông qua giao diện Monad, điều này sẽ cho bạn quyền truy cập vào các hàm tổng quát được định nghĩa trong thư viện. Ví dụ, khi và traverse là các hàm tổng quát. Trong bối cảnh của IO, chúng hoạt động như sau:

when evaluates a computation if a condition is True. It could be used to run some IO actions only on a specific user input.
traverse is similar to map and applies a computation across a structure. For example, you could print every element of a List to the console.

Bạn có thể tìm hiểu thêm về các chức năng này, đặc biệt là kiểu của chúng, bằng cách sử dụng :doc. Danh sách dưới đây cho thấy chúng đang hoạt động trong bối cảnh một phép toán IO.

Listing 12.12.
Using `when` and `traverse` (Traverse.idr)

The application operator $

Hãy nhớ từ chương 10 rằng toán tử $ là một toán tử trung gian áp dụng một hàm cho một đối số. Mục đích chính của nó là giảm bớt sự cần thiết phải sử dụng dấu ngoặc. Trong danh sách 12.12, bạn cũng có thể viết cách áp dụng của khi với dấu ngoặc rõ ràng, như sau:

when (x == "yes") (do traverse putStrLn crew pure ())

Nếu bạn triển khai Functor, Applicative và Monad cho State, bạn sẽ có thể sử dụng những hàm này và những hàm tương tự trong các hàm sử dụng State. Danh sách tiếp theo cho thấy một ví dụ về những gì bạn có thể làm, cung cấp một hàm cộng các số nguyên từ một danh sách vào một tổng tích lũy, miễn là số nguyên đó dương. Hiện tại, điều này sẽ không hợp lệ về mặt kiểu dữ liệu.

Listing 12.13.
Adding positive integers from a list to a state (StateMonad.idr)

Điều này sẽ thất bại vì bạn không có các triển khai của Functor hoặc Applicative cho State:

StateMonad.idr:42:15: When checking right hand side of addIfPositive with expected type State Integer Bool When checking an application of function Main.>>=: Can't find implementation for Applicative (State Integer)

Mục tiêu cuối cùng của bạn ở đây là triển khai Monad cho State, điều này cũng yêu cầu các triển khai của Functor và Applicative. Danh sách tiếp theo hiển thị giao diện Monad, như đã được định nghĩa trong Prelude.

Listing 12.14.
The `Monad` interface

The join method

Chúng tôi chưa xem xét chi tiết về hàm join, nhưng bạn có thể sử dụng nó để làm phẳng các cấu trúc lồng nhau thành một cấu trúc duy nhất. Ví dụ, có các triển khai Monad cho List và Maybe, vì vậy bạn có thể thử hàm join trên các ví dụ của mỗi loại:

Idris< join [[1,2,3], [4,5,6]] [1, 2, 3, 4, 5, 6] : List Integer Idris< join (Just (Just "One")) Just "One" : Maybe String Idris< join (Just (Nothing {a=String})) Nothing : Maybe String

Đối với List, hàm join sẽ nối các danh sách lồng nhau. Đối với Maybe, hàm join sẽ tìm giá trị đơn lẻ nằm trong cấu trúc, nếu có.

Cả hai phương pháp, (>>=) và join, đều có định nghĩa mặc định, vì vậy bạn có thể triển khai Monad bằng cách định nghĩa một hoặc cả hai. Ở đây, chúng ta chỉ sử dụng (>>=).

Nếu bạn muốn cung cấp một triển khai cho Monad, bạn cũng cần phải triển khai Applicative, vì nó là một giao diện cha của Monad. Tương tự, Applicative có một giao diện cha, Functor. Danh sách sau đây hiển thị cả hai giao diện như được định nghĩa trong Prelude.

Listing 12.15.
The `Functor` and `Applicative` interfaces

Phương thức (<*>) cho phép bạn, ví dụ, có một hàm có trạng thái trả về một hàm (có kiểu a -> b), có một hàm có trạng thái khác trả về một đối số (có kiểu a), và áp dụng hàm đó cho đối số.

Bạn có thể bắt đầu bằng cách triển khai Functor như sau:

Type, define—Write the implementation header and create a skeleton definition of map. Remember that you can create skeleton definitions for interface methods by pressing Ctrl-Alt-A with the cursor over the interface name:
```
Functor (State stateType) where map func x = ?Functor_rhs_1
```

Type, refine—The type of the ?Functor_rhs_1 hole tells you that x is a stateful computation:

 stateType : Type b : Type a : Type func : a -> b x : State stateType a -------------------------------------- Functor_rhs_1 : State stateType b

You can continue the definition by extracting the value from the computation x using Bind:

Functor (State stateType) where map func x = Bind x (\val => ?Functor_rhs_1)

Refine— To complete the definition, pass val to func, and use Pure to convert the result to a stateful computation:
```
Functor (State stateType) where map func x = Bind x (\val => Pure (func val))
```

Danh sách 12.16 cho thấy các định nghĩa của Applicative và Monad cho State. Bạn triển khai Applicative theo cách tương tự như Functor, sử dụng Bind để trích xuất các giá trị bạn cần từ các phép toán có trạng thái.

Listing 12.16.
Implementing `Applicative` and `Monad` for `State` (StateMonad.idr)

Bạn đã sử dụng Bind trong các triển khai của Functor và Applicative vì bạn chưa có cú pháp do chưa có. Bạn cần một triển khai Monad để cung cấp nó, và bạn cần có các triển khai Functor và Applicative để có một triển khai Monad.

Nhưng bạn có thể sử dụng cú pháp do bằng cách định nghĩa tất cả các cài đặt cùng nhau, trong một khối chung, như danh sách 12.17 cho thấy. Trong một khối chung, các định nghĩa có thể tham chiếu lẫn nhau, vì vậy các cài đặt của Functor và Applicative có thể dựa vào cài đặt của Monad.

Listing 12.17.
Defining `Functor`, `Applicative`, and `Monad` implementations together (StateMonad.idr)

Bây giờ bạn đã triển khai các giao diện này, bạn có thể thử định nghĩa trước đó của addPositives từ danh sách 12.13:

*StateMonad> runState (addPositives [-4, 3, -8, 9, 8]) 0 (3, 20) : (Nat, Integer)

The Effects library: combining State, IO, and other side effects

Vì bạn đã có các triển khai Monad cho State và IO, việc tuần tự hóa các phép tính có trạng thái và các phép tính tương tác tương ứng là điều hợp lý để tự hỏi liệu bạn có thể tuần tự hóa cả hai cùng một lúc, trong cùng một hàm—thì sao với các chương trình tương tác cũng thao tác trên trạng thái?

Bạn sẽ thấy một cách để làm điều này trong phần tiếp theo. Tuy nhiên, như một giải pháp tổng quát hơn, Idris cung cấp một thư viện gọi là Effects hỗ trợ việc kết hợp các loại tác dụng phụ khác nhau như State và IO trong các kiểu, cũng như các tác động khác như ngoại lệ và tính không xác định. Bạn có thể tìm thêm chi tiết trong hướng dẫn thư viện Effects (http://idris-lang.org/documentation/effects).

Bạn đã thấy cách đóng gói chi tiết của việc thao tác trạng thái bằng cách mô tả các chuỗi hoạt động có trạng thái dưới dạng State và thực thi chúng bằng cách sử dụng runState. Bạn cũng đã thấy cách triển khai Functor, Applicative và Monad cho State.

Các trạng thái mà bạn đã sử dụng trong các ví dụ cho đến nay là khá nhỏ: một dòng nhãn duy nhất hoặc một số nguyên đơn. Nói chung, trạng thái có thể trở nên khá phức tạp:

State may consist of several complex components, stored as a record. We’ll discuss this in the rest of this chapter, where you’ll see how to write a complete interactive program with state.
You might want to use a dependent type in your State, in which case updating the state will also update its type! For example, if you add an element to a Vect 8 Int, it would become a Vect 9 Int. We’ll discuss this in the next chapter.

Một lợi thế của việc viết một kiểu dữ liệu thể hiện các chuỗi lệnh, cùng với một hàm để thực thi những lệnh đó, là bạn có thể làm cho kiểu lệnh chính xác như bạn cần. Như bạn sẽ thấy trong phần tiếp theo, bạn có thể mô tả một cách chính xác tập hợp các lệnh bạn cần cho một ứng dụng cụ thể, bao gồm các lệnh cho tương tác tại console và các lệnh để đọc và ghi các thành phần của trạng thái ứng dụng. Trong chương tiếp theo, bạn sẽ thấy cách bạn có thể mô tả chính xác trong kiểu của nó tác động mà mỗi lệnh có đến trạng thái của hệ thống.

12.3. A complete program with state: working with records

Trong chương trước, bạn đã thực hiện một bài kiểm tra toán học đưa ra các bài toán nhân cho người dùng và theo dõi số lượng câu trả lời đúng và câu hỏi đã được hỏi. Trong phần này, chúng ta sẽ viết một phiên bản tinh chỉnh, với những cải tiến sau:

We’ll add a difficulty setting, which specifies the largest number allowed when generating questions.
Instead of passing the current score as an argument to the quiz function, maintaining the state by hand, we’ll extend the Command type with commands for giving access to the current score and the difficulty setting.

Để viết phiên bản tinh chỉnh này, chúng ta sẽ cần suy nghĩ lại cách đại diện cho trạng thái của trò chơi. Chúng ta sẽ làm điều này bằng cách sử dụng các loại bản ghi. Bạn đã thấy một số cách sử dụng bản ghi để đại diện cho kho dữ liệu trong chương 6, với các ví dụ tương tự trong các chương 7 và 10. Tuy nhiên, khi trạng thái của một ứng dụng phát triển, việc chia trạng thái của nó thành nhiều bản ghi phân cấp có thể là hợp lý.

Bạn sẽ thấy cách định nghĩa và sử dụng các bản ghi lồng nhau, cách cập nhật các bản ghi với cú pháp ngắn gọn, và cách sử dụng một bản ghi để lưu trữ trạng thái của chương trình quiz tương tác. Nhưng trước tiên, chúng ta sẽ xem lại kiểu Command từ chương 11 và xem cách bạn có thể mở rộng nó để hỗ trợ việc đọc và ghi trạng thái hệ thống, theo cách tương tự như kiểu State tùy chỉnh được định nghĩa trong phần trước.

12.3.1.
Interactive programs with state: the arithmetic quiz revisited

Trong chương 11, bạn đã định nghĩa một kiểu dữ liệu Command, đại diện cho các lệnh mà bạn có thể sử dụng trong các chương trình I/O trên console, và một kiểu ConsoleIO, đại diện cho các quá trình tương tác có thể kéo dài vô hạn. Bạn đã sử dụng điều này để triển khai một bài kiểm tra toán học, đưa ra các bài toán nhân để người dùng trả lời. Tương tự như State, mô tả các thao tác Get và Put để đọc và ghi trạng thái, Command mô tả các thao tác GetLine và PutStr để đọc từ và ghi vào console. Dưới đây là danh sách tóm tắt các định nghĩa của Command và ConsoleIO.

Listing 12.18.
Interactive programs supporting only console I/O (ArithState.idr)

Implementing Monad for Command

Cũng như với State, bạn có thể triển khai Functor, Applicative và Monad cho Command thay vì triển khai trực tiếp (>>=). Như một bài tập, hãy thử cung cấp các triển khai cho mỗi loại. Như tôi đã lưu ý trong chương trước, tuy nhiên, bạn không thể cung cấp một triển khai Monad cho ConsoleIO vì kiểu của ConsoleDo.(>>=) không khớp.

Giống như runState, mà nhận mô tả về các thao tác có trạng thái và trả về kết quả của việc thực hiện các thao tác đó với một trạng thái ban đầu, run nhận một mô tả về các thao tác tương tác và thực hiện chúng trong IO. Danh sách 12.19 tóm tắt hàm run. Hãy nhớ rằng bạn giới hạn thời gian chạy của các chương trình tương tác bằng cách sử dụng kiểu Fuel, và bạn thêm một hàm không tổng quát, forever, cho phép một chương trình tương tác tổng quát chạy vô hạn, trong khi chỉ giới thiệu một hàm không tổng quát duy nhất.

Listing 12.19.
Running interactive programs (ArithState.idr)

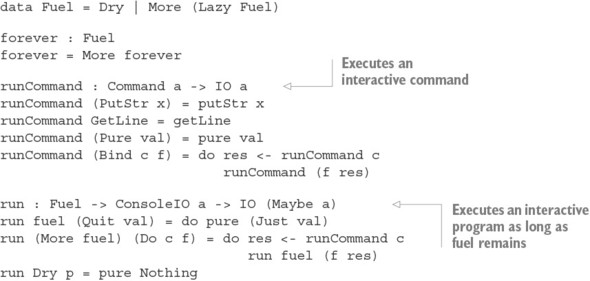
Nếu bạn muốn các chương trình tương tác của mình có khả năng đọc và ghi trạng thái, ngoài việc đọc từ và ghi vào bảng điều khiển, bạn có thể mở rộng kiểu Command với các lệnh bổ sung để thao tác với trạng thái và xử lý các lệnh đó giống như bạn đã làm với State. Đối với trò chơi toán học, chúng ta cần thực hiện các bước sau:

Get random numbers for the questions, given the game’s difficulty setting.
Read the current game state so that you can display the score.
Update the game state so that you can update the score according to the user’s answers.

Danh sách tiếp theo cho thấy cách bạn có thể mở rộng kiểu dữ liệu Command để bao gồm các lệnh này. Không cần phải cập nhật ConsoleIO, vì nó chỉ đơn giản là sắp xếp các Command.

Listing 12.20.
Extending the `Command` type to support game state (ArithState.idr)

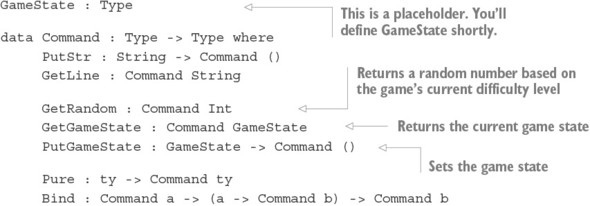
`GameState hiện tại chưa được định nghĩa, vì vậy bạn chưa thể hoàn thành lệnh chạy hoặc lệnh chạy. Tuy nhiên, bạn có thể thêm các điều kiện mẫu với các khoảng trống cho các lệnh bổ sung để thỏa mãn chỉ số toàn vẹn:`

runCommand : Command a -> IO a runCommand (PutStr x) = putStr x runCommand GetLine = getLine runCommand (Pure val) = pure val runCommand (Bind c f) = do res <- runCommand c runCommand (f res) runCommand (PutGameState x) = ?runCommand_rhs_1 runCommand GetGameState = ?runCommand_rhs_2 runCommand GetRandom = ?runCommand_rhs_3

Adding missing cases

Sau khi bạn đã thêm các hàm khởi tạo vào Command, bạn có thể sử dụng Ctrl-Alt-A với con trỏ chuột đặt trên runCommand trong phần khai báo kiểu để thêm các điều khoản mẫu mới cho runCommand.

Bạn sẽ sử dụng kiểu GameState để lưu trữ trạng thái của trò chơi. Trước khi bạn triển khai bài kiểm tra tinh chỉnh, do đó, bạn cần xem xét cách định nghĩa GameState.

12.3.2.
Complex state: defining nested records

Trong triển khai quiz tinh chỉnh, bạn sẽ sử dụng GameState để lưu trữ các thông tin sau:

The current score, consisting of the number of questions answered correctly and the number attempted
The difficulty setting

Khi có nhiều thành phần trong trạng thái của một chương trình như vậy, thường thì việc sử dụng loại bản ghi là hợp lý. Bản ghi rất tiện lợi vì chúng sinh ra các hàm chiếu, cho phép bạn kiểm tra các trường của bản ghi. Bạn cũng có thể lồng ghép các bản ghi; danh sách sau đây cho thấy cách bạn có thể biểu diễn điểm số hiện tại dưới dạng một bản ghi, và trạng thái tổng thể của trò chơi dưới dạng một bản ghi, bao gồm bản ghi điểm số lồng bên trong như một trường.

Listing 12.21.
Representing a game state as nested records (ArithState.idr)

Việc định nghĩa Score và GameState dưới dạng các bản ghi sẽ tự động tạo ra các hàm chiếu cho từng trường: correct, attempted, score và difficulty. Ví dụ, bạn có thể lấy cấp độ độ khó như sau:

*ArithState> difficulty initState 12 : Int

Hoặc bạn có thể lấy số câu trả lời đúng cho đến nay:

*ArithState> correct (score initState) 0 : Nat

Records and namespaces

Khi bạn định nghĩa một bản ghi, các hàm chiếu được định nghĩa trong không gian tên riêng của chúng, được đặt theo tên của bản ghi. Ví dụ, hàm điểm được định nghĩa trong một không gian tên GameState mới, như bạn có thể thấy với :doc tại REPL:

*ArithState> :doc score Main.GameState.score : (rec : GameState) -> Score

Điều này cho phép cùng một tên trường được sử dụng nhiều lần trong cùng một mô-đun. Ví dụ, bạn có thể sử dụng một trường có tên là title trong hai bản ghi khác nhau trong cùng một tệp, Record.idr:

record Book where constructor MkBook title : String author : String record Album where constructor MkAlbum title : String tracks : List String

Idris sẽ quyết định phiên bản tiêu đề nào để sử dụng, tùy theo ngữ cảnh:

*Record> title (MkBook "Breakfast of Champions" "Kurt Vonnegut") "Breakfast of Champions" : String

Danh sách dưới đây cho thấy cách bạn có thể sử dụng các hàm chiếu để định nghĩa một triển khai của Show cho GameState.

Listing 12.22.
`Show` implementation for `GameState` (ArithState.idr)

Show GameState where show st = show (correct (score st)) ++ "/" ++ show (attempted (score st)) ++ "\n" ++ "Difficulty: " ++ show (difficulty st)

Bạn có thể thử điều này tại REPL, sử dụng printLn để hiển thị trạng thái trò chơi ban đầu:

*ArithState> :exec printLn initState 0/0 Difficulty: 12

Do đó, các bản ghi cung cấp cho bạn một ký hiệu thuận tiện để kiểm tra các giá trị trường, nhưng khi bạn viết chương trình sử dụng bản ghi để giữ trạng thái, bạn cũng sẽ cần cập nhật các trường. Trong bài kiểm tra, ví dụ, bạn sẽ cần tăng điểm số và số câu hỏi đã cố gắng.

12.3.3.
Updating record field values

Idris là một ngôn ngữ hàm thuần túy, vì vậy bạn sẽ không cập nhật các trường của bản ghi trực tiếp. Thay vào đó, khi chúng ta nói rằng chúng ta đang cập nhật một bản ghi, chúng ta thực sự có nghĩa là chúng ta đang xây dựng một bản ghi mới chứa nội dung của bản ghi cũ với một trường thay đổi. Ví dụ, danh sách sau đây cho thấy một cách để trả về một bản ghi mới với trường độ khó được cập nhật, sử dụng khớp mẫu.

Listing 12.23.
Setting a record field by pattern matching (ArithState.idr)

setDifficulty : Nat -> GameState -> GameState setDifficulty newDiff (MkGameState score _) = MkGameState score newDiff

Nếu bản ghi có nhiều trường, điều này có thể trở nên không thuận tiện rất nhanh chóng, vì bạn sẽ cần viết các hàm cập nhật cho mỗi trường. Không chỉ vậy, nếu bạn muốn thêm một trường vào bản ghi, bạn sẽ cần phải sửa đổi tất cả các hàm cập nhật. Do đó, Idris cung cấp một cú pháp tích hợp sẵn để cập nhật các trường trong bản ghi. Dưới đây là một triển khai của setDifficulty sử dụng cú pháp cập nhật bản ghi.

Listing 12.24.
Setting a record field using record-update syntax (ArithState.idr)

setDifficulty : Nat -> GameState -> GameState setDifficulty newDiff state = record { difficulty = newDiff } state

Hình 12.3 cho thấy các thành phần của cú pháp cập nhật bản ghi. Lưu ý đặc biệt rằng cú pháp cập nhật bản ghi tự nó là một kiểu hạng nhất, trong đó từ khóa "record" bắt đầu một bản cập nhật bản ghi, vì vậy bản cập nhật này có một kiểu. Ở đây, bản cập nhật có kiểu hàm, GameState -> GameState, vì vậy bạn cũng có thể triển khai setDifficulty như sau:

setDifficulty : Nat -> GameState -> GameState setDifficulty newDiff = record { difficulty = newDiff }

Figure 12.3.
Syntax for returning a new record with a field updated

Bạn có thể cập nhật các trường ghi chú lồng nhau theo cách tương tự, bằng cách chỉ định đường dẫn đến trường mà bạn muốn cập nhật. Danh sách sau đây cho thấy cách bạn có thể viết các hàm đúng và sai, nhằm cập nhật điểm số.

Listing 12.25.
Setting nested record fields using record-update syntax (ArithState.idr)

Ghi chú `score->attempted` cung cấp đường dẫn đến trường mà bạn muốn cập nhật, với tên trường ngoài cùng ở đầu tiên. Vì vậy, trong ví dụ này, bạn muốn cập nhật trường attempted của trường score trong bản ghi state.

12.3.4.
Updating record fields by applying functions

Cú pháp cập nhật bản ghi cung cấp một ký hiệu ngắn gọn để chỉ định một đường dẫn đến một trường bản ghi cụ thể. Tuy nhiên, nó vẫn hơi bất tiện vì bạn cần phải viết rõ ràng đường dẫn đến mỗi trường hai lần, theo hai cách ký hiệu khác nhau.

First, to find the field to update, using the score->correct path notation
Second, to find the old value, using a function application, correct (score state)

Do đó, Idris cung cấp một ký hiệu để cập nhật các trường của bản ghi bằng cách áp dụng trực tiếp một hàm vào giá trị hiện tại của trường. Danh sách tiếp theo cho thấy một cách ngắn gọn để cập nhật các trường bản ghi lồng ghép trong GameState.

Listing 12.26.
Updating nested record fields by directly applying functions to the current value of the field (ArithState.idr)

Updating records with $=

Bạn đã thấy toán tử $, áp dụng một hàm cho một đối số, trong chương 10. Cú pháp $= xuất phát từ sự kết hợp giữa toán tử áp dụng hàm $ và cú pháp cập nhật bản ghi.

Cú pháp này cung cấp cho bạn một cách viết hàm ngắn gọn và thuận tiện để cập nhật các trường bản ghi lồng nhau, giúp dễ dàng hơn trong việc viết chương trình thao tác với trạng thái. Hơn nữa, vì nó không sử dụng khớp mẫu, nó độc lập với bất kỳ trường nào khác trong một bản ghi, vì vậy ngay cả khi bạn thêm các trường vào bản ghi GameState, addWrong và addCorrect vẫn sẽ hoạt động mà không cần chỉnh sửa.

12.3.5.
Implementing the quiz

Sử dụng loại Lệnh mới của bạn và bản ghi GameState, bạn có thể triển khai bài kiểm tra toán học bằng cách đọc và cập nhật trạng thái khi cần thiết. Danh sách tiếp theo hiển thị một phác thảo của việc triển khai bài kiểm tra, để lại chỗ trống cho câu đáp đúng và câu đáp sai, mà lần lượt xử lý một câu trả lời đúng và một câu trả lời sai.

Listing 12.27.
Implementing the arithmetic quiz (ArithState.idr)

Điều này tương tự như việc triển khai bài kiểm tra ở cuối chương 11, nhưng thay vì truyền dòng số ngẫu nhiên và điểm số làm tham số, bạn coi mỗi cái trong số chúng như là trạng thái mà bạn đọc và ghi theo yêu cầu. Điều này đơn giản hóa định nghĩa của bài kiểm tra, nhưng làm cho định nghĩa của ConsoleIO phức tạp hơn.

Danh sách tiếp theo cho thấy cách bạn có thể triển khai đúng và sai, mỗi cái sẽ sửa đổi trạng thái bằng cách sử dụng addCorrect và addWrong, tương ứng, như đã được định nghĩa trong phần trước.

Listing 12.28.
Processing correct and wrong answers by updating the game state (ArithState.idr)

Ở giai đoạn này, bạn đã có một mô tả đầy đủ về một bài quiz toán tương tác mà lấy số ngẫu nhiên và điểm số hiện tại từ trạng thái. Nó cũng tổng cộng:

*ArithState> :total quiz Main.quiz is Total

Nhưng để chạy quiz, bạn sẽ cần mở rộng hàm runCommand để hỗ trợ các lệnh mới của bạn.

12.3.6.
Running interactive and stateful programs: executing the quiz

Cũng như với hàm runState mà bạn đã viết để xử lý các phép toán trong kiểu State tùy chỉnh ở mục 12.2, hàm run đã được cập nhật sẽ cần xử lý trạng thái trò chơi hiện tại. Nó cũng sẽ cần đọc từ một luồng số ngẫu nhiên (cho Get-Random) và thực hiện I/O trên console. Bảng liệt kê sau đây cho thấy cách tất cả những điều này được ghi nhận trong một loại mới cho runCommand.

Listing 12.29.
A new type and skeleton definition for `runCommand` (ArithState.idr)

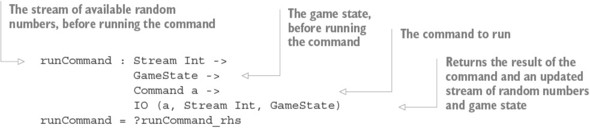
Danh sách 12.30 cung cấp định nghĩa hoàn chỉnh của hàm runCommand. Lưu ý rằng, trong từng trường hợp, bạn cần trả về kết quả của lệnh cũng như chỉ ra cách mỗi lệnh ảnh hưởng đến luồng số ngẫu nhiên và trạng thái trò chơi.

Listing 12.30.
The complete definition of `runCommand` (ArithState.idr)

Tương tự, bạn cần cập nhật hàm run để nhận một luồng các số nguyên ngẫu nhiên và trạng thái trò chơi ban đầu. Giống như hàm runCommand, hàm run cũng trả về kết quả của việc chạy chương trình, cùng với luồng và trạng thái trò chơi đã được cập nhật. Dưới đây là phiên bản mới của hàm run, hỗ trợ trạng thái trò chơi.

Listing 12.31.
Running a `ConsoleIO` program consisting of a potentially infinite stream of `Command` (ArithState.idr)

run : Fuel -> Stream Int -> GameState -> ConsoleIO a -> IO (Maybe a, Stream Int, GameState) run fuel rnds state (Quit val) = do pure (Just val, rnds, state) run (More fuel) rnds state (Do c f) = do (res, newRnds, newState) <- runCommand rnds state c run fuel newRnds newState (f res) run Dry rnds state p = pure (Nothing, rnds, state)

Như trong chương 11, bạn sử dụng Fuel để chỉ ra khoảng thời gian bạn sẵn sàng cho phép một chương trình tương tác có thể vô hạn chạy, vì vậy phần của kiểu trả về đại diện cho kết quả của việc thực thi chương trình, kiểu ConsoleIO a, có kiểu Maybe a, để nắm bắt khả năng hết Fuel.

Cuối cùng, danh sách tiếp theo cho thấy cách bạn cập nhật chương trình chính để khởi tạo luồng số ngẫu nhiên và trạng thái trò chơi.

Listing 12.32.
A `main` program that initializes the arithmetic quiz with a random number stream and an initial state (ArithState.idr)

Cũng như việc triển khai bài kiểm tra ở cuối chương 11, bạn tách biệt các chuỗi lệnh kết thúc (sử dụng loại Command) khỏi các chuỗi thao tác I/O đa phương tiện trong console có thể không kết thúc (sử dụng loại ConsoleIO). Ngoài ra, bạn mở rộng loại Command để cho phép đọc và ghi lại trạng thái của trò chơi tương tự như việc triển khai của State. Nếu bạn định nghĩa một loại cụ thể cho các lệnh mà một ứng dụng có thể thực thi, bạn có thể làm cho loại đó chính xác như bạn cần, có thể mô tả tác động của mỗi thao tác đối với một sự trừu tượng của trạng thái hệ thống. Bạn sẽ thấy nhiều hơn về những gì bạn có thể đạt được bằng cách làm theo mẫu này và những đảm bảo mà bạn có thể đưa ra về các chương trình tương tác có trạng thái trong chương tiếp theo.

Exercises

Write an updateGameState function with the following type:
```
updateGameState : (GameState -> GameState) -> Command ()
```
You can test it by using it in the definitions of correct and wrong instead of GetGameState and PutGameState. For example:
```
correct : ConsoleIO GameState correct = do PutStr "Correct!\n" updateGameState addCorrect quiz
```
Implement the Functor, Applicative, and Monad interfaces for Command.

You could define records for representing an article on a social news website as follows, along with the number of times the article has been upvoted or downvoted:

record Votes where constructor MkVotes upvotes : Integer downvotes : Integer record Article where constructor MkArticle title : String url : String score : Votes initPage : (title : String) -> (url : String) -> Article initPage title url = MkArticle title url (MkVotes 0 0)

Write a function to calculate the overall score of a given article, where the score is calculated from the number of downvotes subtracted from the number of upvotes. It should have the following type:

getScore : Article -> Integer

You can test it with the following example articles:

badSite : Article badSite = MkArticle "Bad Page" "http://example.com/bad" (MkVotes 5 47) goodSite : Article goodSite = MkArticle "Good Page" "http://example.com/good" (MkVotes 101 7)

At the REPL, you should see the following:

*ex_12_3> getScore goodSite 94 : Integer *ex_12_3> getScore badSite -42 : Integer

Write addUpvote and addDownvote functions that modify an article’s score up or down. They should have the following types:

addUpvote : Article -> Article addDownvote : Article -> Article

You can test these at the REPL as follows:

*ex_12_3> addUpvote goodSite MkArticle "Good Page" "http://example.com/good" (MkVotes 102 7) : Article *ex_12_3> addDownvote badSite MkArticle "Bad Page" "http://example.com/bad" (MkVotes 5 48) : Article *ex_12_3> getScore (addUpvote goodSite) 95 : Integer

12.4. Summary

Many algorithms read and write state. For example, when labeling the nodes of a tree in depth-first order, you can keep track of the state of the labels while traversing the tree.
You can manage state by using the generic State type to describe operations on the state along with a runState function to execute those operations.
You can define your own State type as a sequence of Get and Put operations.
Defining Functor, Applicative, and Monad for the State type gives you access to several generic functions from the Idris library.
When writing interactive programs with state, you can define a Command type to describe an interface consisting of console I/O and state management operations.
Record types can represent more complex nested state.
Idris provides a concise syntax for assigning new values to fields in nested records.
Idris also provides a syntax (using $=) for updating a field in a nested record by applying a function to the value in that field.

Chapter 13.
State machines: verifying protocols in types

Chương này đề cập đến

Specifying protocols in types
Describing preconditions and postconditions of operations
Using dependent types in state

Trong chương trước, bạn đã thấy cách quản lý trạng thái có thể thay đổi bằng cách định nghĩa một loại để đại diện cho các chuỗi lệnh trong một hệ thống, và một hàm để thực hiện những lệnh đó. Điều này theo một mẫu thường gặp: kiểu dữ liệu mô tả một chuỗi các phép toán, và hàm diễn giải chuỗi đó trong một ngữ cảnh cụ thể. Ví dụ, State mô tả các chuỗi phép toán có trạng thái, và runState diễn giải những phép toán đó với một trạng thái ban đầu cụ thể.

Trong chương này, chúng ta sẽ xem xét một trong những lợi thế của việc sử dụng kiểu để mô tả các chuỗi thao tác và giữ chức năng thực thi tách biệt. Nó cho phép bạn làm cho các mô tả chính xác hơn, để một số thao tác chỉ có thể được thực hiện khi trạng thái có một hình thức cụ thể. Ví dụ, một số thao tác yêu cầu truy cập vào một tài nguyên, chẳng hạn như một tay cầm tệp hoặc kết nối cơ sở dữ liệu, trước khi chúng được thực thi:

You need an open file handle to read from a file successfully.
You need a connection to a database before you can run a query on the database.

Khi bạn viết các chương trình làm việc với các tài nguyên như thế này, bạn thực sự đang làm việc với một máy trạng thái. Một khách hàng cơ sở dữ liệu có thể có hai trạng thái, chẳng hạn như Đóng và Kết nối, ám chỉ đến trạng thái kết nối của nó với cơ sở dữ liệu. Một số thao tác (chẳng hạn như truy vấn cơ sở dữ liệu) chỉ hợp lệ trong trạng thái Kết nối; một số thao tác (chẳng hạn như kết nối với cơ sở dữ liệu) chỉ hợp lệ trong trạng thái Đóng; và một số thao tác (chẳng hạn như kết nối và đóng) cũng thay đổi trạng thái của hệ thống. Hình 13.1 minh họa hệ thống này.

Figure 13.1.
A state transition diagram showing the high-level operation of a database. It has two possible states, `Closed` and `Connected`. Its three operations, `Connect`, `Query`, and `Close`, are only valid in specific states.

Các máy trạng thái như hình minh họa trong hình 13.1 tồn tại, một cách ngầm, trong nhiều hệ thống thực tế. Khi bạn triển khai các hệ thống giao tiếp, chẳng hạn, qua mạng hoặc sử dụng các quy trình đồng thời, bạn cần đảm bảo mỗi bên tuân theo cùng một mẫu giao tiếp, nếu không, hệ thống có thể rơi vào tình trạng deadlock hoặc hành xử theo cách khác không mong đợi. Mỗi bên theo một máy trạng thái, nơi việc gửi hoặc nhận một tin nhắn đưa hệ thống tổng thể vào một trạng thái mới, vì vậy điều quan trọng là mỗi bên phải tuân theo một giao thức được định nghĩa rõ ràng. Trong Idris, chúng tôi có một hệ thống kiểu biểu đạt, vì vậy nếu có một mô hình cho một giao thức, thì tốt nhất là diễn đạt điều đó trong một kiểu, để bạn có thể sử dụng kiểu đó giúp thực hiện giao thức một cách chính xác.

Trong chương này, bạn sẽ thấy cách để tạo ra các máy trạng thái như cái được minh họa trong hình 13.1 một cách rõ ràng trong kiểu. Bằng cách này, bạn có thể chắc chắn rằng bất kỳ hàm nào mô tả chính xác một chuỗi hành động đều tuân theo giao thức được định nghĩa bởi một máy trạng thái. Không chỉ vậy, bạn có thể áp dụng cách tiếp cận dựa trên kiểu để định nghĩa các chuỗi hành động bằng cách sử dụng các khoảng trống và phát triển tương tác. Chúng ta sẽ bắt đầu với một số ví dụ tương đối trừu tượng để minh họa cách bạn có thể mô tả các máy trạng thái trong kiểu, mô hình hóa các trạng thái và hoạt động trên một cánh cửa và một máy bán hàng tự động.

13.1. State machines: tracking state in types

Bạn đã từng triển khai các chương trình có trạng thái bằng cách định nghĩa một kiểu mô tả các lệnh để đọc và ghi trạng thái. Với các loại phụ thuộc, bạn có thể làm cho các loại lệnh này chính xác hơn và bao gồm bất kỳ chi tiết nào liên quan đến trạng thái của hệ thống trong chính kiểu đó.

Ví dụ, hãy xem xét cách thể hiện trạng thái của một cánh cửa với chuông cửa. Một cánh cửa có thể ở một trong hai trạng thái, mở (được biểu diễn là DoorOpen) hoặc đóng (được biểu diễn là DoorClosed), và chúng tôi sẽ cho phép ba thao tác:

Opening the door, which moves the system from the DoorClosed state to the DoorOpen state
Closing the door, which moves the system from the DoorOpen state to the DoorClosed state
Ringing the doorbell, which we’ll only allow when the door is in the DoorClosed state

Hình 13.2 là một sơ đồ chuyển trạng thái cho thấy các trạng thái mà hệ thống có thể ở và cách mỗi hoạt động thay đổi trạng thái tổng thể.

Figure 13.2.
A state transition diagram showing the states and operations on a door

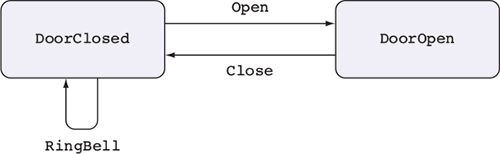
Nếu bạn có thể định nghĩa các chuyển trạng thái này trong một kiểu, thì một mô tả có kiểu đúng về một chuỗi các phép toán phải tuân theo đúng các quy tắc được hiển thị trong sơ đồ chuyển trạng thái. Hơn nữa, bạn sẽ có thể sử dụng các khoảng trống và chỉnh sửa tương tác để tìm hiểu các phép toán nào là hợp lệ tại một thời điểm cụ thể trong chuỗi.

Trong phần này, bạn sẽ thấy cách định nghĩa máy trạng thái như cửa trong một loại phụ thuộc. Đầu tiên, chúng tôi sẽ triển khai một mô hình của cửa, và sau đó chúng tôi sẽ mô hình hóa các trạng thái phức tạp hơn trong mô hình của một máy bán hàng tự động đơn giản. Trong mỗi trường hợp, chúng tôi sẽ tập trung vào mô hình các chuyển trạng thái, thay vì một triển khai cụ thể của máy.

13.1.1.
Finite state machines: modeling a door as a type

Máy trạng thái trong hình 13.2 mô tả một giao thức để sử dụng cửa đúng cách bằng cách chỉ ra các thao tác hợp lệ trong trạng thái nào, và các thao tác đó ảnh hưởng đến trạng thái như thế nào. Danh sách 13.1 cho thấy một cách để biểu diễn các thao tác có thể có. Điều này cũng bao gồm một bộ tạo (>>=) để thực hiện chuỗi và một bộ tạo Pure để sản xuất các giá trị thuần túy.

Listing 13.1.
Representing operations on a door as a command type (Door.idr)

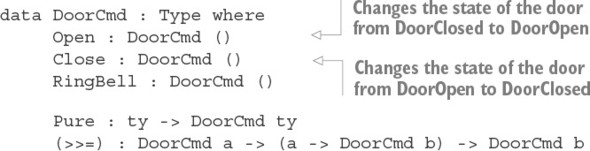
Reminder: (>>=) and do notation

Hãy nhớ rằng cú pháp do được dịch thành các phép áp dụng của (>>=).

Với DoorCmd, bạn có thể viết các hàm như sau, mô tả một chuỗi các thao tác để rung chuông cửa và mở sau đó đóng cửa, đúng theo quy trình sử dụng cửa.

doorProg : DoorCmd () doorProg = do RingBell Open Close

Thật không may, bạn cũng có thể mô tả các chuỗi thao tác không hợp lệ không tuân theo giao thức, chẳng hạn như sau, khi bạn cố gắng mở một cánh cửa hai lần, và sau đó bấm chuông cửa khi cánh cửa đã mở:

doorProgBad : DoorCmd () doorProgBad = do Open Open RingBell

Bạn có thể tránh điều này và giới hạn các chức năng với DoorCmd cho các chuỗi hoạt động hợp lệ tuân theo giao thức bằng cách theo dõi trạng thái của cửa trong kiểu của các hoạt động DoorCmd. Danh sách sau đây cho thấy cách thực hiện điều này, mô tả chính xác các chuyển trạng thái được thể hiện trong hình 13.2 trong các kiểu của các lệnh.

Listing 13.2.
Modeling the door state machine in a type, describing state transitions in the types of the commands (Door.idr)

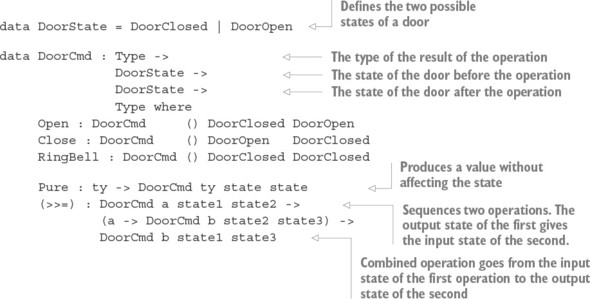
Mỗi loại lệnh đều nhận ba đối số:

The type of the value produced by the command
The input state of the door; that is, the state the door must be in before you can execute the operation
The output state of the door; that is, the state the door will be in after you execute the operation

Việc triển khai hàm sau đây sẽ mô tả một chuỗi hành động bắt đầu và kết thúc với cánh cửa đóng.

doorProg : DoorCmd () DoorClosed DoorClosed

Argument order in DoorCmd

Lưu ý rằng kiểu mà một chuỗi các phép toán tạo ra là tham số đầu tiên cho DoorCmd, và nó được theo sau bởi các trạng thái đầu vào và đầu ra. Đây là một quy ước phổ biến khi định nghĩa các kiểu để mô tả sự chuyển trạng thái, và nó sẽ trở nên quan trọng trong chương 14 khi chúng ta xem xét các máy trạng thái phức tạp hơn liên quan đến lỗi và phản hồi từ môi trường.

Nói chung, nếu bạn có một giá trị của kiểu DoorType ty trướcState sauState, nó mô tả một chuỗi các hành động của cửa tạo ra một giá trị của kiểu ty; nó bắt đầu với cửa ở trạng thái trướcState; và nó kết thúc với cửa ở trạng thái sauState.

13.1.2.
Interactive development of sequences of door operations

Để thấy cách các kiểu trong DoorCmd có thể giúp bạn viết đúng các chuỗi hoạt động, hãy cùng tái triển khai doorProg. Chúng ta sẽ viết điều này giống như trước: bấm chuông cửa, mở cửa và đóng cửa.

Nếu bạn viết nó theo từng bước, bạn sẽ thấy cách kiểu dữ liệu thể hiện những thay đổi trong trạng thái của cánh cửa qua từng hành động.

Define— Begin with the skeleton definition:

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = ?doorProg_rhs

Refine, type—Add an action to ring the doorbell:
```
doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell ?doorProg_rhs
```
If you check the type of ?doorProg_rhs now, you’ll see that it should be a sequence of actions that begins and ends with the door in the DoorClosed state:
```
-------------------------------------- doorProg_rhs : DoorCmd () DoorClosed DoorClosed
```

Refine, type—Next, add an action to open the door:

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open ?doorProg_rhs

If you check the type of ?doorProg_rhs now, you’ll see that it should begin with the door in the DoorOpen state instead:

-------------------------------------- doorProg_rhs : DoorCmd () DoorOpen DoorClosed

Refine failure—If you add an extra Open now, with the door already in the DoorOpen state, you’ll get a type error:

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open Open ?doorProg_rhs

The error says that the type of Open is an operation that starts in the DoorClosed state, but the expected type starts in the DoorOpen state:

Door.idr:20:15: When checking right hand side of doorProg with expected type DoorCmd () DoorClosed DoorClosed When checking an application of constructor Main.>>=: Type mismatch between DoorCmd () DoorClosed DoorOpen (Type of Open) and DoorCmd a DoorOpen state2 (Expected type) Specifically: Type mismatch between DoorClosed and DoorOpen

Refine— Instead, complete the definition by closing the door:

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open Close

Defining preconditions and postconditions in types

Loại doorProg bao gồm các trạng thái đầu vào và đầu ra cung cấp các điều kiện tiên quyết và hậu quả cho chuỗi (cửa phải được đóng cả trước và sau chuỗi). Nếu định nghĩa vi phạm bất kỳ điều nào, bạn sẽ gặp lỗi kiểu.

Ví dụ, bạn có thể quên đóng cửa.

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open

Trong trường hợp này, bạn sẽ nhận được một lỗi kiểu.

Door.idr:18:15: When checking right hand side of doorProg with expected type DoorCmd () DoorClosed DoorClosed When checking an application of constructor Main.>>=: Type mismatch between DoorCmd () DoorClosed DoorOpen (Type of Open) and DoorCmd () DoorClosed DoorClosed (Expected type) Specifically: Type mismatch between DoorOpen and DoorClosed

Lỗi này đề cập đến bước cuối cùng và nói rằng Open chuyển từ DoorClosed sang DoorOpen, nhưng loại mong đợi là chuyển từ DoorClosed sang DoorClosed.

Bằng cách định nghĩa DoorCmd theo cách này, với các trạng thái đầu vào và đầu ra rõ ràng trong kiểu, bạn đã định nghĩa điều gì có nghĩa là một chuỗi các thao tác cửa là hợp lệ. Và bằng cách viết doorProg một cách từng bước, với một chuỗi các bước và một chỗ trống cho phần còn lại của định nghĩa, bạn có thể thấy trạng thái của cửa ở mỗi giai đoạn bằng cách nhìn vào kiểu của chỗ trống.

Cửa có chính xác hai trạng thái, CửaĐóng và CửaMở, và bạn có thể mô tả chính xác khi nào bạn thay đổi trạng thái từ trạng thái này sang trạng thái kia trong các loại hoạt động của cửa. Nhưng không phải tất cả các hệ thống đều có một số lượng trạng thái chính xác mà bạn có thể xác định trước. Tiếp theo, chúng ta sẽ xem xét cách bạn có thể mô hình hóa các hệ thống với số lượng trạng thái có thể vô hạn.

13.1.3.
Infinite states: modeling a vending machine

Trong phần này, chúng ta sẽ mô hình hóa một máy bán hàng tự động bằng cách sử dụng phát triển dựa trên kiểu, viết các kiểu mô tả rõ ràng trạng thái đầu vào và đầu ra của từng thao tác. Như một sự đơn giản hóa, máy chỉ chấp nhận một loại tiền xu (xu £1) và phân phối một sản phẩm (thanh sô-cô-la). Dù vậy, có thể có số lượng tiền xu hoặc thanh sô-cô-la tùy ý trong máy, vì vậy số trạng thái khả dĩ không phải là hữu hạn.

Bảng 13.1 mô tả các hoạt động cơ bản của một máy bán hàng tự động, cùng với trạng thái của máy trước và sau mỗi hoạt động.

Table 13.1.
Vending machine operations, with input and output states represented as `Nat`

Tiền xu (trước)	Sô cô la (trước)	Hoạt động	Tiền xu (sau)	Sô cô la (sau)
pounds	chocs	Insert coin	S pounds	chocs
S pounds	S chocs	Vend chocolate	pounds	chocs
pounds	chocs	Return coins	Z	chocs

Giống như ví dụ về cửa, mỗi thao tác đều có điều kiện tiên quyết và điều kiện hậu quả:

Precondition— The number of coins and amount of chocolate that must be in the machine before the operation
Postcondition— The number of coins and amount of chocolate in the machine after the operation.

Bạn có thể đại diện cho trạng thái của máy dưới dạng một cặp hai số tự nhiên, số đầu tiên đại diện cho số tiền xu trong máy và số thứ hai đại diện cho số viên sô-cô-la.

VendState : Type VendState = (Nat, Nat)

Danh sách tiếp theo cho thấy một đại diện của trạng thái máy bán hàng dưới dạng kiểu Idris, với các chuyển trạng thái từ bảng 13.1 được viết rõ ràng trong các loại thao tác MachineCmd.

Listing 13.3.
Modeling the vending machine in a type, describing state transitions in the types of commands (Vending.idr)

Để hoàn thành mô hình, bạn cần có khả năng tuần tự hóa các lệnh. Bạn cũng cần có khả năng đọc đầu vào từ người dùng: các lệnh mà bạn đang xác định mô tả những gì máy móc làm, nhưng cũng có một giao diện người dùng bao gồm những điều sau đây:

A coin slot
A vend button, for dispensing chocolate
A change button, for returning any unused coins

Bạn có thể mô hình hóa những hoạt động này trong một kiểu dữ liệu để mô tả các đầu vào có thể của người dùng. Danh sách 13.4 cho thấy mô hình hoàn chỉnh của máy bán hàng tự động, bao gồm các hoạt động bổ sung để hiển thị tin nhắn (Display), nạp đầy máy (Refill) và đọc các hành động của người dùng (GetInput).

Listing 13.4.
The complete model of vending machine state (Vending.idr)

13.1.4.
A verified vending machine description

Danh sách 13.5 cho thấy cấu trúc của một hàm mô tả các chuỗi thao tác đã được xác minh cho một máy bán hàng tự động sử dụng các chuyển trạng thái được định nghĩa bởi MachineCmd. Miễn là nó được kiểm tra kiểu, bạn biết rằng bạn đã sắp xếp đúng các thao tác, và bạn sẽ không bao giờ thực hiện một thao tác mà không đáp ứng điều kiện tiên quyết của nó.

Listing 13.5.
A main loop that reads and processes user input to the vending machine (Vending.idr)

Có các lỗ để bán và nạp lại. Trong mỗi trường hợp, bạn cần kiểm tra rằng số lượng tiền xu và sô cô la thỏa mãn các điều kiện tiên quyết của chúng. Nếu bạn cố gắng bán mà không kiểm tra điều kiện tiên quyết, Idris sẽ báo lỗi:

Idris sẽ báo lỗi vì bạn chưa kiểm tra xem có tiền xu trong máy và thanh chocolate có sẵn hay không, vì vậy điều kiện tiên quyết có thể không được thỏa mãn.

Vending.idr:67:13: When checking right hand side of vend with expected type MachineIO (pounds, chocs) When checking an application of function Main.MachineDo.>>=: Type mismatch between MachineCmd () (S pounds1, S chocs2) (pounds1, chocs2) (Type of Vend) and MachineCmd () (pounds, chocs) (pounds1, chocs2) (Expected type) Specifically: Type mismatch between S chocs1 and chocs

Lỗi cho biết rằng trạng thái đầu vào phải có dạng (S pounds1, S chocs2), nhưng thay vào đó nó có dạng (pounds, chocs).

Bạn có thể giải quyết vấn đề này bằng cách ghép mẫu trên các đối số ngụ ý, pounds và chocs, để đảm bảo chúng ở dạng đúng, hoặc hiển thị lỗi nếu không. Danh sách sau đây cho thấy các định nghĩa của vend và refill thực hiện điều này.

Listing 13.6.
Adding definitions of `vend` and `refill` that check that their preconditions are satisfied (Vending.idr)

Với cả cửa và máy bán hàng, chúng tôi đã sử dụng kiểu để mô hình hóa các trạng thái của một hệ thống vật lý. Trong mỗi trường hợp, kiểu cung cấp một sự tr抽象 về trạng thái mà hệ thống đang ở trước và sau mỗi thao tác, và các giá trị trong kiểu mô tả các chuỗi thao tác hợp lệ. Chúng tôi chưa triển khai một hàm chạy để thực hiện các chuyển đổi trạng thái cho cả DoorCmd hay MachineCmd, nhưng trong mã đi kèm với cuốn sách này, có sẵn trực tuyến, bạn sẽ tìm thấy mã thực hiện một mô phỏng bảng điều khiển của máy bán hàng.

Trong phần tiếp theo, bạn sẽ thấy một ví dụ cụ thể hơn về việc theo dõi trạng thái trong kiểu dữ liệu, thực hiện một cấu trúc dữ liệu ngăn xếp. Tôi sẽ sử dụng ví dụ này để minh họa cách bạn có thể thực thi các lệnh trong thực tế.

Exercises

Change the RingBell operation so that it works in any state, rather than only when the door is closed. You can test your answer by seeing that the following function type-checks:
```
doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open RingBell Close
```
The following (incomplete) type defines a command for a guessing game, where the input and output states are the number of remaining guesses allowed:
```
data GuessCmd : Type -> Nat -> Nat -> Type where Try : Integer -> GuessCmd Ordering ?in_state ?out_state Pure : ty -> GuessCmd ty state state (>>=) : GuessCmd a state1 state2 -> (a -> GuessCmd b state2 state3) -> GuessCmd b state1 state3
```
The Try command returns an Ordering that says whether the guess was too high, too low, or correct, and that changes the number of available guesses. Complete the type of Try so that you can only make a guess when there’s at least one guess allowed, and so that guessing reduces the number of guesses available. If you have a correct answer, the following definition should type-check:
```
threeGuesses: GuessCmd () 3 0 threeGuesses = do Try 10 Try 20 Try 15 Pure ()
```
Also, the following definition shouldn’t type-check:
```
noGuesses : GuessCmd () 0 0 noGuesses = do Try 10 Pure ()
```

The following type defines the possible states of matter:

data Matter = Solid | Liquid | Gas

Define a MatterCmd type in such a way that the following definitions type-check:

iceSteam : MatterCmd () Solid Gas iceSteam = do Melt Boil steamIce : MatterCmd () Gas Solid steamIce = do Condense Freeze

Additionally, the following definition should not type-check:

overMelt : MatterCmd () Solid Gas overMelt = do Melt Melt

13.2. Dependent types in state: implementing a stack

Bạn đã thấy cách mô hình hóa các trạng thái chuyển tiếp trong một kiểu cho hai ví dụ trừu tượng: một cái cửa (đại diện cho việc nó mở hay đóng trong kiểu của nó) và một máy bán hàng tự động (đại diện cho nội dung của nó trong kiểu). Việc lưu trữ thông tin trừu tượng này trong kiểu của các thao tác là đặc biệt hữu ích khi bạn cũng có dữ liệu cụ thể liên quan đến dữ liệu trừu tượng đó. Ví dụ, nếu bạn đang mô tả dữ liệu có kích thước cụ thể, và kiểu của một thao tác cho bạn biết nó thay đổi kích thước của dữ liệu như thế nào, bạn có thể sử dụng Vect như là một đại diện cụ thể. Bạn sẽ biết độ dài cần thiết của Vect đầu vào và đầu ra từ kiểu của mỗi thao tác.

Trong phần này, bạn sẽ thấy cách hoạt động của nó bằng cách thực hiện các thao tác trên cấu trúc dữ liệu ngăn xếp. Ngăn xếp là một cấu trúc dữ liệu theo nguyên tắc vào sau ra trước, nơi bạn có thể thêm các mục vào và loại bỏ chúng từ đỉnh của ngăn xếp, và chỉ có mục ở trên cùng là có thể truy cập được. Ngăn xếp hỗ trợ ba thao tác:

Push—Adds a new item to the top of the stack
Pop—Removes the top item from the stack, provided that the stack isn’t empty
Top—Inspects the top item on the stack, provided that the stack isn’t empty

Giống như các thao tác trên máy bán hàng tự động, mỗi thao tác này đều có một điều kiện tiền đề mô tả trạng thái đầu vào cần thiết và một điều kiện hậu đề mô tả trạng thái đầu ra. Bảng 13.2 mô tả những điều này, cung cấp kích thước ngăn xếp cần thiết trước mỗi thao tác và kích thước ngăn xếp sau khi thực hiện thao tác.

Table 13.2.
Stack operations, with input and output stack sizes represented as `Nat`

Kích thước ngăn xếp (trước)	Hoạt động	Kích thước ngăn xếp (sau)
height	Push element	S height
S height	Pop element	height
S height	Inspect top element	S height

Bạn sẽ diễn đạt các điều kiện tiên quyết và điều kiện hậu quả trong các kiểu của mỗi thao tác. Khi bạn đã định nghĩa các thao tác trên một ngăn xếp, bạn sẽ triển khai một hàm để thực hiện các chuỗi thao tác ngăn xếp bằng cách sử dụng một đại diện cụ thể của ngăn xếp với chiều cao trong kiểu của nó. Bởi vì bạn đang sử dụng chiều cao của ngăn xếp trong các chuyển tiếp trạng thái, một đại diện cụ thể tốt cho một ngăn xếp là Vect. Bạn biết rằng, ví dụ, một ngăn xếp các số nguyên có chiều cao 10 chứa chính xác 10 số nguyên, vì vậy bạn có thể đại diện điều này như một giá trị của kiểu Vect 10 Integer.

Cuối cùng, bạn sẽ thấy một ví dụ về ngăn xếp đang hoạt động, triển khai một máy tính tương tác dựa trên ngăn xếp.

13.2.1.
Representing stack operations in a state machine

Cũng như với DoorCmd và MachineCmd trong phần 13.1, chúng tôi sẽ mô tả các thao tác trên một ngăn xếp trong một loại phụ thuộc và đặt các thuộc tính quan trọng của trạng thái đầu vào và đầu ra một cách rõ ràng trong loại đó. Ở đây, thuộc tính của trạng thái mà chúng tôi quan tâm là chiều cao của ngăn xếp.

Danh sách 13.7 cho thấy cách bạn có thể biểu diễn các phép toán trong bảng 13.2 bằng mã, mô tả cách mỗi phép toán ảnh hưởng đến chiều cao của ngăn xếp. Trong ví dụ này, bạn chỉ lưu trữ các giá trị kiểu Integer trên ngăn xếp, nhưng bạn có thể mở rộng StackCmd để cho phép ngăn xếp tổng quát bằng cách tham số hóa qua kiểu phần tử trong ngăn xếp.

Listing 13.7.
Representing operations on a stack data structure with the input and output heights of the stack in the type (Stack.idr)

Bạn đang sử dụng một Vect để đại diện cho ngăn xếp, vì vậy mỗi lần bạn thêm một phần tử vào vector hoặc loại bỏ một phần tử, bạn sẽ thay đổi kiểu của vector. Do đó, bạn đang đại diện cho trạng thái biến phụ thuộc bằng cách đưa các tham số liên quan vào kiểu (độ dài của Vect) trong chính kiểu StateCmd.

Sử dụng StackCmd, bạn có thể viết các chuỗi hoạt động trên ngăn xếp mà ở đó chiều cao đầu vào và đầu ra của ngăn xếp được thể hiện rõ trong các kiểu dữ liệu. Ví dụ, hàm sau đây đẩy hai số nguyên vào ngăn xếp, lấy ra hai số nguyên và sau đó trả về tổng của chúng:

testAdd : StackCmd Integer 0 0 testAdd = do Push 10 Push 20 val1 <- Pop val2 <- Pop Pure (val1 + val2)

Các loại của các constructor trong StackCmd đảm bảo rằng sẽ luôn có một phần tử trên ngăn xếp khi bạn cố gắng gọi Pop. Ví dụ, nếu bạn chỉ đẩy một số nguyên trong testAdd, Idris sẽ báo lỗi:

Khi bạn cố gắng định nghĩa testAdd như thế này, Idris báo lỗi:

Stack.idr:27:22: When checking right hand side of testAdd with expected type StackCmd Integer 0 0 When checking an application of constructor Main.>>=: Type mismatch between StackCmd Integer (S height) height (Type of Pop) and StackCmd a 0 height2 (Expected type) Specifically: Type mismatch between S height and 0

Lỗi này, và đặc biệt là sự không khớp giữa chiều cao S và 0, có nghĩa là bạn có một ngăn xếp có chiều cao 0, nhưng Pop cần một ngăn xếp chứa ít nhất một phần tử.

Cách tiếp cận này tương tự như các hàm có trạng thái được định nghĩa trong chương 12, ở đây sử dụng Push và Pop để mô tả cách bạn đang sửa đổi và truy vấn trạng thái. Như với các mô tả trước đó về chuỗi các thao tác có trạng thái, bạn sẽ cần viết một hàm riêng để chạy những chuỗi đó.

13.2.2.
Implementing the stack using Vect

Danh sách 13.8 cho thấy cách thực hiện một hàm thực thi các thao tác trên ngăn xếp. Điều này giống như runState mà bạn đã thấy trong chương 12, nhưng ở đây bạn nhận một đầu vào Vect có chiều cao đúng như nội dung của ngăn xếp.

Listing 13.8.
Executing a sequence of actions on a stack, using a `Vect` to represent the stack’s contents

Nếu bạn thử chạy runStack với testAdd, truyền vào một ngăn xếp ban đầu rỗng, bạn sẽ thấy rằng nó trả về tổng của hai phần tử mà bạn đẩy vào, và ngăn xếp cuối cùng là rỗng.

*Stack> runStack [] testAdd (30, []) : (Integer, Vect 0 Integer)

Bạn cũng có thể định nghĩa các hàm như sau, hàm này cộng hai phần tử trên cùng của ngăn xếp và đưa kết quả trở lại ngăn xếp:

doAdd : StackCmd () (S (S height)) (S height) doAdd = do val1 <- Pop val2 <- Pop Push (val1 + val2)

Trạng thái đầu vào S (chiều cao S) có nghĩa là ngăn xếp phải có ít nhất hai phần tử, nhưng có thể có bất kỳ chiều cao nào khác. Nếu bạn thử thực hiện doAdd với một ngăn xếp ban đầu chứa hai phần tử, bạn sẽ thấy rằng nó tạo ra một ngăn xếp chứa một phần tử duy nhất là tổng của hai phần tử đầu vào.

*Stack> runStack [2,3] doAdd ((), [5]) : ((), Vect 1 Integer)

Nếu trạng thái đầu vào chứa nhiều hơn hai phần tử, bạn sẽ thấy rằng nó tạo ra một ngăn xếp có chiều cao nhỏ hơn một so với chiều cao đầu vào. Ví dụ, một ngăn xếp đầu vào là [2, 3, 4] dẫn đến một ngăn xếp đầu ra có giá trị [2 + 3, 4]:

*Stack> runStack [2,3,4] doAdd ((), [5, 4]) : ((), Vect 2 Integer)

Bạn có thể thêm hai phần tử trên ngăn xếp kết quả bằng cách gọi doAdd một lần nữa:

*Stack> runStack [2,3,4] (do doAdd; doAdd) ((), [9]) : ((), Vect 1 Integer)

Nhưng việc cố gắng thêm một doAdd nữa sẽ gây ra lỗi kiểu, vì chỉ còn một phần tử trên ngăn xếp.

*Stack> runStack [2,3,4] (do doAdd; doAdd; doAdd) (input):1:34:When checking an application of constructor Main.>>=: Type mismatch between StackCmd () (S (S height)) (S height) (Type of doAdd) and StackCmd ty 1 outHeight (Expected type) Specifically: Type mismatch between S height and 0

Lỗi này có nghĩa là bạn cần có S (chiều cao S) phần tử trên ngăn xếp (tức là, ít nhất hai phần tử) nhưng bạn chỉ có chiều cao S (tức là, ít nhất một, nhưng không nhất thiết phải nhiều hơn). Bằng cách đặt chiều cao của ngăn xếp trong kiểu, bạn đã chỉ định rõ ràng các điều kiện tiền đề và hậu đề cho mỗi thao tác, vì vậy bạn sẽ nhận được lỗi kiểu nếu vi phạm bất kỳ điều nào trong số này.

13.2.3.
Using a stack interactively: a stack-based calculator

Nếu bạn thêm các lệnh để đọc từ và ghi vào bảng điều khiển, bạn có thể viết một ứng dụng bảng điều khiển để thao tác với stack và triển khai một máy tính dựa trên stack. Người dùng có thể nhập một số, điều này sẽ đẩy số vào stack, hoặc nhập "add", điều này sẽ cộng hai mục trên cùng của stack, đẩy kết quả vào stack và hiển thị kết quả. Một phiên làm việc điển hình có thể như sau:

Hình 13.3 cho thấy cách thức mà mỗi đầu vào hợp lệ trong phiên này ảnh hưởng đến nội dung của ngăn xếp. Mỗi khi người dùng nhập một số nguyên, kích thước ngăn xếp tăng lên một, và mỗi khi người dùng nhập lệnh cộng, kích thước ngăn xếp giảm đi một, miễn là có hai mục để cộng.

Figure 13.3.
How each user input affects the contents of the stack

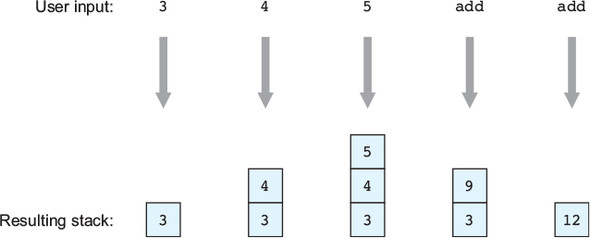
Để triển khai chương trình ngăn xếp tương tác này, bạn sẽ cần mở rộng StackCmd để hỗ trợ đọc và ghi từ và đến bảng điều khiển. Danh sách sau đây cho thấy StackCmd trong một tệp mới, StackIO.idr, được mở rộng với hai lệnh: GetStr và PutStr.

Listing 13.9.
Extending `StackCmd` to support console I/O with the commands `GetStr` and `PutStr` (StackIO.idr)

Dependent states in the Effects library

Tôi đã đề cập đến thư viện Effects trong chương 12, cho phép bạn kết hợp các hiệu ứng như trạng thái và đầu vào/đầu ra console mà không cần phải định nghĩa một kiểu mới, như StackCmd ở đây. Thư viện Effects hỗ trợ mô tả các chuyển đổi trạng thái và trạng thái phụ thuộc như trong StackCmd. Tôi sẽ không mô tả thêm về thư viện Effects trong cuốn sách này, nhưng việc tìm hiểu về các nguyên tắc của trạng thái phụ thuộc ở đây sẽ có nghĩa là bạn sẽ có thể dễ dàng học cách sử dụng thư viện Effects linh hoạt hơn.

Bạn cũng sẽ cần cập nhật runStack để hỗ trợ hai lệnh mới. Bởi vì GetStr và PutStr mô tả các hành động tương tác, bạn sẽ cần cập nhật kiểu của runStack để trả về các hành động IO. Đây là runStack đã được cập nhật.

Listing 13.10.
Updating `runStack` to support the interactive commands `GetStr` and `PutStr` (StackIO.idr)

runStack : (stk : Vect inHeight Integer) -> StackCmd ty inHeight outHeight -> IO (ty, Vect outHeight Integer) runStack stk (Push val) = pure ((), val :: stk) runStack (val :: stk) Pop = pure (val, stk) runStack (val :: stk) Top = pure (val, val :: stk) runStack stk GetStr = do x <- getLine pure (x, stk) runStack stk (PutStr x) = do putStr x pure ((), stk) runStack stk (Pure x) = pure (x, stk) runStack stk (x >>= f) = do (x', newStk) <- runStack stk x runStack newStk (f x')

Cũng giống như với máy bán hàng tự động, bạn sẽ mô tả các chuỗi vô hạn các thao tác StackCmd trong các hàm tổng quát bằng cách định nghĩa một kiểu StackIO riêng để mô tả các luồng thao tác ngăn xếp vô hạn. Danh sách sau đây cho thấy cách bạn có thể định nghĩa StackIO và cách chạy các chuỗi StackIO, với một trạng thái ban đầu cho ngăn xếp.

Listing 13.11.
Defining infinite sequences of interactive stack operations (StackIO.idr)

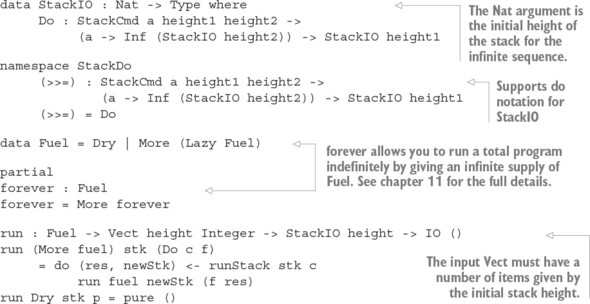
Máy tính tương tác tuân theo một mẫu tương tự như việc triển khai máy bán hàng tự động. Danh sách tiếp theo cho thấy một phác thảo của vòng lặp chính, đọc một đầu vào, phân tích nó thành loại lệnh, và xử lý lệnh nếu đầu vào là hợp lệ.

Listing 13.12.
Outline of an interactive stack-based calculator (StackIO.idr)

Bạn vẫn cần định nghĩa strToInput, hàm phân tích cú pháp đầu vào của người dùng, và tryAdd, hàm thêm hai phần tử ở đầu ngăn xếp, nếu có thể. Danh sách sau đây cho thấy định nghĩa của strToInput.

Listing 13.13.
Reading user input for the stack-based calculator (StackIO.idr)

Cuối cùng, danh sách tiếp theo hiển thị định nghĩa của tryAdd. Giống như vend và refill trong việc triển khai máy bán hàng, bạn cần phải kiểm tra trạng thái ban đầu để đảm bảo rằng có đủ mặt hàng trên ngăn xếp để thêm vào.

Listing 13.14.
Adding the top two elements on the stack, if they’re present (StackIO.idr)

Bạn có thể kiểm tra rằng stackCalc là tổng ở REPL:

*StackIO> :total stackCalc Main.stackCalc is Total

Bằng cách tách biệt thành phần lặp (StackIO) khỏi thành phần kết thúc (StackCmd), và bằng cách chỉ định các kiểu chính xác cho các phép toán, bạn có thể chắc chắn rằng stackCalc có ít nhất các thuộc tính sau đây, miễn là nó là toàn phần:

It will continue running indefinitely.
It will never crash due to user input that isn’t handled.
It will never crash due to a stack overflow.

Exercises

Add user commands to the stack-based calculator for subtract and multiply. You can test these as follows:
```
*ex_13_2> :exec > 5 > 3 > subtract 2 > 8 > multiply 16
```
Add a negate user command to the stack-based calculator for negating the top item on the stack. You can test this as follows:
```
> 10 > negate -10
```
Add a discard user command that removes the top item from the stack. You can test this as follows:
```
> 3 > 4 > discard Discarded 4 > add Fewer than two items on the stack
```
Add a duplicate user command that duplicates the top item on the stack. You can test this as follows:
```
> 2 > duplicate Duplicated 2 > add 4
```

13.3. Summary

Data types can model state machines by using each data constructor to describe a state transition.
You can describe how a command changes the state of a system by giving the input and output states of the system as part of the command’s type.
Developing sequences of state transitions interactively, using holes, means you can check the required input and output states of a sequence of commands.
Types can model infinite state spaces as well as finite states.
Sequences of commands give verified sequences of state transitions because a sequence of commands will only type-check if it describes a valid sequence of state transitions.
You can represent mutable dependently typed state by putting the arguments to the dependent type in the state transitions. For example, you can use the length of a vector to represent the height of a stack.

Chapter 14.
Dependent state machines: handling feedback and errors

Chương này đề cập đến

Handling errors in state transitions
Developing protocol implementations interactively
Guaranteeing security properties in types

Như bạn đã thấy trong chương trước, bạn có thể mô tả các chuyển đổi trạng thái hợp lệ của một máy trạng thái trong một kiểu phụ thuộc, được chỉ mục bởi trạng thái đầu vào yêu cầu của một phép toán (điều kiện tiên quyết) và trạng thái đầu ra (điều kiện hậu quả). Bằng cách định nghĩa các chuyển đổi trạng thái hợp lệ trong kiểu, bạn có thể chắc chắn rằng một chương trình đã kiểm tra kiểu sẽ được đảm bảo mô tả một chuỗi chuyển đổi trạng thái hợp lệ.

Bạn đã thấy hai ví dụ, một mô tả về một cánh cửa và một mô phỏng về một máy bán hàng tự động, và trong mỗi trường hợp, chúng tôi đã đưa ra các loại chính xác cho các hoạt động để mô tả cách chúng ảnh hưởng đến trạng thái. Nhưng chúng tôi đã không xem xét khả năng rằng bất kỳ hoạt động nào cũng có thể thất bại:

What if, when you try to open the door, it’s jammed? What if, even though you’ve run the Open operation, it’s still in the DoorClosed state?
What if, when you insert a coin in the vending machine, the machine rejects the coin?

Trong hầu hết các tình huống thực tế, khi bạn cố gắng gán các kiểu chính xác để mô tả một máy trạng thái, bạn sẽ cần xem xét khả năng thao tác thất bại hoặc một phản hồi không mong đợi:

Like the DoorState, you might represent the state of a file handle (open or closed) in a type, but if you try to open a file, the file might not exist or you might not have permission to open it.
You might represent a secure communication protocol in a state machine, but whether you can progress in the protocol depends on receiving valid responses from the network to any request you send.
You might represent the state of a bank’s automated teller machine (ATM) in a type (waiting for a card, waiting for PIN entry, and so on), but you can only move to a state where the machine can dispense cash if checking the user’s PIN is successful.

Trong những trường hợp này, bạn không hoàn toàn kiểm soát cách mà trạng thái hệ thống thay đổi. Bạn có thể yêu cầu thay đổi trạng thái (mở một tệp, gửi một tin nhắn, v.v.) nhưng việc trạng thái thay đổi trong thực tế phụ thuộc vào phản hồi mà bạn nhận được từ môi trường. Trong chương này, bạn sẽ thấy cách xử lý khả năng một thao tác thất bại bằng cách cho phép một trạng thái chuyển tiếp phụ thuộc vào kết quả của thao tác.

Bạn cũng sẽ thấy cách xử lý các thay đổi trạng thái có thể phụ thuộc vào đầu vào của người dùng—chúng ta sẽ xem xét các chuyển đổi trạng thái liên quan đến việc mô hình hóa một máy ATM, nơi đầu vào của người dùng xác định xem máy có thể phát tiền hay không. Chúng ta sẽ bắt đầu bằng cách xem lại mô hình của cánh cửa từ chương 13 và xem cách xử lý khả năng rằng cánh cửa có thể bị kẹt, khiến cho thao tác Mở bị thất bại.

14.1. Dealing with errors in state transitions

Trong chương trước, bạn đã định nghĩa một kiểu dữ liệu DoorCmd để mô hình hóa các chuyển đổi trạng thái trên một cánh cửa, như đã minh họa bởi sơ đồ chuyển đổi trạng thái trong hình 14.1.

Figure 14.1.
A state transition diagram showing the states and operations on a door

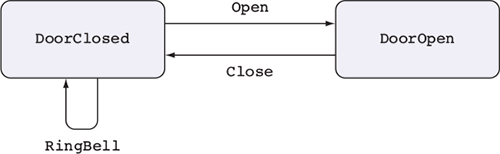
Danh sách 14.1 tóm tắt định nghĩa của DoorCmd, mô hình hóa hệ thống chuyển trạng thái trong hình 14.1.

Listing 14.1.
Modeling the door state machine in a type

data DoorState = DoorClosed | DoorOpen data DoorCmd : Type -> DoorState -> DoorState -> Type where Open : DoorCmd () DoorClosed DoorOpen Close : DoorCmd () DoorOpen DoorClosed RingBell : DoorCmd () DoorClosed DoorClosed Pure : ty -> DoorCmd ty state state (>>=) : DoorCmd a state1 state2 -> (a -> DoorCmd b state2 state3) -> DoorCmd b state1 state3

Trong mô hình này, bạn hoàn toàn kiểm soát cách mỗi hoạt động chuyển từ trạng thái này sang trạng thái khác. Ví dụ, loại trạng thái Mở mà nó luôn bắt đầu với một cánh cửa ở trạng thái CửaĐóng, và nó luôn kết thúc với một cánh cửa ở trạng thái CửaMở.

Open : DoorCmd () DoorClosed DoorOpen

Thực tế không phải lúc nào cũng thuận lợi, tuy nhiên! Nếu bạn thực hiện điều này với một số phần cứng thực sự, chẳng hạn như một cánh cửa trượt được điều khiển bằng cách nhấn nút, bạn sẽ cần phải xem xét khả năng xảy ra sự cố phần cứng như cánh cửa bị kẹt. Trong phần này, chúng ta sẽ cải tiến mô hình cánh cửa để nắm bắt khả năng xảy ra lỗi này, và xem xét cách điều này ảnh hưởng đến việc triển khai các chương trình theo giao thức.

14.1.1.
Refining the door model: representing failure

Mở có thể thất bại do cửa bị kẹt, vì vậy chúng ta cần một cách để biểu thị liệu nó có thành công hay không. Chúng ta có thể định nghĩa một kiểu định danh để mô tả các kết quả có thể của việc mở cửa:

data DoorResult = OK | Jammed

Sau đó, thay vì trả về giá trị đơn vị, Open có thể trả về một DoorResult. Chúng ta có thể thử kiểu sau cho Open:

Open : DoorCmd DoorResult DoorClosed DoorOpen

Rất tiếc, điều này không hoàn toàn đúng vì nó vẫn nói rằng việc mở cửa khiến cửa ở trạng thái DoorOpen, bất kể điều gì xảy ra. Chúng ta cần tìm cách diễn đạt rằng việc Mở cửa khiến cửa ở trạng thái DoorClosed hoặc DoorOpen, tùy thuộc vào giá trị của DoorResult mà nó tạo ra. Hình 14.2 minh họa máy trạng thái mà chúng ta muốn triển khai.

Figure 14.2.
A state transition diagram showing the states and operations on a door, where opening the door might fail

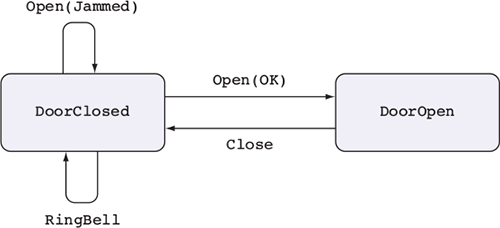
Bạn có thể đạt được điều này bằng cách thay đổi kiểu của DoorCmd để cho phép trạng thái đầu ra được tính toán từ giá trị trả về. Hình 14.3 minh họa cách bạn có thể tinh chỉnh kiểu của DoorCmd để đạt được điều này.

Figure 14.3.
New type for `DoorCmd`, where the output state of an operation is computed from the return value of the operation

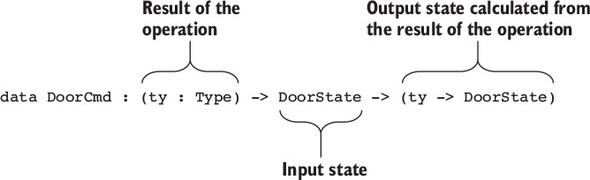
Ở đây, bạn đã đặt tên cho kiểu trả về của thao tác, ty, và đã nói rằng trạng thái đầu ra được tính toán bởi một hàm nhận ty làm đầu vào. Bây giờ, khi bạn định nghĩa kiểu của Open (và thực tế là tất cả các thao tác DoorCmd), bạn đưa ra một biểu thức cho trạng thái đầu ra, giải thích cách mà trạng thái đầu ra được tính toán từ giá trị trả về, có kiểu DoorResult:

Open : DoorCmd DoorResult DoorClosed (\res => case res of OK => DoorOpen Jammed => DoorClosed)

Điều này mã hóa chính xác những gì sơ đồ chuyển trạng thái trong hình 14.2 minh họa. Cụ thể, trạng thái đầu ra của Open có thể là một trong các trạng thái sau:

DoorOpen—If Open returns OK
DoorClosed—If Open returns Jammed

Mặc dù bạn sẽ không biết giá trị của res cho đến khi thực hiện thao tác, nhưng bạn ít nhất có thể sử dụng kiểu để giải thích các trạng thái có thể có của cánh cửa dựa trên kết quả của Open. Danh sách 14.2 cho thấy khai báo kiểu DoorCmd hoàn chỉnh sau khi tinh chỉnh này. Nó cũng thêm Display, vì vậy bạn có thể hiển thị các thông báo ghi log nếu cần thiết.

Listing 14.2.
The refined `DoorCmd` type, allowing the output state of each operation to be computed from the return value of the operation (DoorJam.idr)

Calculating output state with const

Đây là loại hằng số, được định nghĩa trong Prelude:

*DoorJam> :t const const : a -> b -> a

Nó bỏ qua đối số thứ hai và trả về đối số đầu tiên. Vì vậy, nếu bạn nói const Door-Closed cho trạng thái đầu ra của một thao tác, điều đó sẽ cho bạn một hàm mà bỏ qua kết quả của hàm và luôn trả về DoorClosed.

Trong định nghĩa trước của DoorCmd, trong danh sách 14.1, bạn đã sử dụng toán tử (>>=) để giải thích rằng trạng thái đầu ra của phép toán đầu tiên nên là trạng thái đầu vào của phép toán thứ hai:

(>>=) : DoorCmd a state1 state2 -> (a -> DoorCmd b state2 state3) -> DoorCmd b state1 state3

Bây giờ nó hơi phức tạp hơn, vì giá trị trả về của phép toán đầu tiên ảnh hưởng đến trạng thái đầu vào của phép toán thứ hai:

(>>=) : DoorCmd a state1 state2_fn -> ((res : a) -> DoorCmd b (state2_fn res) state3_fn) -> DoorCmd b state1 state3_fn

Điều này hoạt động như sau:

The first operation returns a value of type a, and the output state is computed from a state2_fn function once you know the result of the operation.
When you come to the second operation, you’ll know the result of the first operation, named res, so it has an input state of state2_fn res.
The combined operation has an input state of state1 (the input state of the first operation) and an output state computed from the result of the second operation, using state3_fn.

Việc định nghĩa DoorCmd theo cách này mang lại cho bạn độ chính xác hơn trong việc xác định các chuyển trạng thái, và điều đó có nghĩa là khi bạn định nghĩa các hàm sử dụng DoorCmd, các loại hoạt động yêu cầu bạn thực hiện bất kỳ kiểm tra cần thiết nào trước khi tiếp tục. Ví dụ, sau khi bạn cố gắng mở cửa, bạn không thể thực hiện bất kỳ thao tác cửa nào khác cho đến khi bạn đã kiểm tra kết quả. Chúng ta sẽ xem xét cách thức hoạt động này bằng cách xem lại ví dụ trước đó của chúng ta, doorProg.

14.1.2.
A verified, error-checking, door-protocol description

Trong chương 13, bạn đã triển khai một hàm sử dụng DoorCmd như một chuỗi hành động để rung chuông, mở và sau đó đóng cửa, và bạn đã sử dụng các kiểu để xác minh rằng chuỗi hành động là hợp lệ. Bạn đã viết doorProg như sau:

doorProg : DoorCmd () DoorClosed DoorClosed doorProg = do RingBell Open Close

Bây giờ mà bạn đã tinh chỉnh loại DoorCmd để trạng thái đầu ra được tính toán từ kết quả của phép toán, bạn sẽ cần viết loại này theo cách khác:

doorProg : DoorCmd () DoorClosed (const DoorClosed)

Điều này có nghĩa là, trạng thái đầu ra không bị ảnh hưởng bởi kết quả, nên bạn sử dụng const, cái sẽ bỏ qua tham số thứ hai và trả về tham số đầu tiên mà không thay đổi. Nhưng nếu bạn cố gắng triển khai doorProg như trước, mà không kiểm tra kết quả của Open, bạn sẽ gặp lỗi:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell Open Close

Lỗi xảy ra khi bạn cố gắng sử dụng Close. Kiểu của nó yêu cầu trạng thái đầu vào là DoorOpen, nhưng thực tế trạng thái đầu vào được tính toán từ kết quả của Open.

When checking an application of constructor Main.>>=: Type mismatch between DoorCmd () DoorOpen (const DoorClosed) (Type of Close) and DoorCmd () ((\res => case res of OK => DoorOpen Jammed => DoorClosed) _) (\value => DoorClosed) (Expected type)

Để xem cách tránh vấn đề này, bạn có thể phát triển doorProg một cách tương tác, bắt đầu từ điểm sau:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell Open ?doorProg_rhs

Debugging type errors using holes

Nếu bạn gặp lỗi kiểu mà khó hiểu khi đứng một mình, thường thì một ý tưởng hay là thay thế phần gây lỗi của chương trình bằng một chỗ trống (như chúng tôi đã làm bằng cách thay thế Close bằng ?doorProg_rhs), để xem kiểu mong đợi là gì, cùng với bất kỳ biến cục bộ nào trong phạm vi.

Type, refine—If you check the type of ?doorProg_rhs, you’ll see this:
```
-------------------------------------- doorProg_rhs : DoorCmd () (case _ of OK => DoorOpen Jammed => DoorClosed) (\value => DoorClosed)
```
The output state you see here arises from the definition of const in the Prelude, and it’s a function that ignores its argument value and returns DoorClosed. The input state you’re looking for is calculated from some value, _. This value is the result of Open, which you haven’t named. Let’s call it jam:
```
doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell jam <- Open ?doorProg_rhs
```

Type— You’ll now see that the input state of the next operation is calculated from the value of jam:

 jam : DoorResult -------------------------------------- doorProg_rhs : DoorCmd () (case jam of OK => DoorOpen Jammed => DoorClosed) (\value => DoorClosed)

Define, type—Because the input state depends on the value of jam, you can make progress by inspecting the value of jam:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell jam <- Open case jam of case_val => ?doorProg_rhs

You’ll now see that the input state depends on the value of case_val:

 case_val : DoorResult jam : DoorResult -------------------------------------- doorProg_rhs : DoorCmd () (case case_val of OK => DoorOpen Jammed => DoorClosed) (\value => DoorClosed)

Define, type—If you case-split on case_val, you should see that each branch of the case has a different type, calculated from the specific value of case_val:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell jam <- Open case jam of OK => ?doorProg_rhs_1 Jammed => ?doorProg_rhs_2

In ?doorProg_rhs_1, for example, jam has the value OK, so the door must have successfully opened:

 jam : DoorResult -------------------------------------- doorProg_rhs_1 : DoorCmd () DoorOpen (\value => DoorClosed)

In ?doorProg_rhs_2, on the other hand, the door is jammed, so it’s still in the DoorClosed state:

 jam : DoorResult -------------------------------------- doorProg_rhs_2 : DoorCmd () DoorClosed (\value => DoorClosed)

Refine— To complete the definition, you can display a log message in each case, and if the door is open, close it again:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell jam <- Open case jam of OK => do Display "Glad To Be Of Service" Close Jammed => Display "Door Jammed"

Loại Mở có nghĩa là bạn cần kiểm tra trạng thái của cửa trước khi thực hiện bất kỳ thao tác nào khác cần biết trạng thái của cửa. Cụ thể, bạn không thể Đóng cửa trừ khi bạn đã mở thành công nó. Tuy nhiên, bạn không cần phải kiểm tra ngay lập tức. Ví dụ, bạn có thể hiển thị một thông điệp giữa việc mở cửa và kiểm tra kết quả.

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell jam <- Open Display "Trying to open the door" case jam of OK => do Display "Glad To Be Of Service" Close Jammed => Display "Door Jammed"

Điều này là hợp lệ, vì điều kiện tiên quyết trên Display không yêu cầu cửa phải ở một trạng thái cụ thể; bất kỳ trạng thái nào cũng được, và Display sẽ không thay đổi trạng thái đó.

Sử dụng các ràng buộc theo mẫu, mà bạn đã thấy lần đầu trong chương 5, bạn cũng có thể định nghĩa doorProg một cách ngắn gọn hơn, như sau:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell OK <- Open | Jammed => Display "Door Jammed" Display "Glad To Be Of Service" Close

Điều này cung cấp một con đường mặc định qua chuỗi hành động, khi Open trả về OK, và một hành động thay thế khi Open trả về Jammed. Việc sử dụng các ràng buộc theo mẫu giúp dễ dàng hơn trong việc viết các chuỗi hành động dài hơn, trong đó một số hành động có thể thất bại. Ví dụ, bạn có thể mở và đóng cửa hai lần và từ bỏ chuỗi nếu bất kỳ hành động nào thất bại:

doorProg : DoorCmd () DoorClosed (const DoorClosed) doorProg = do RingBell OK <- Open | Jammed => Display "Door Jammed" Display "Glad To Be Of Service" Close OK <- Open | Jammed => Display "Door Jammed" Display "Glad To Be Of Service" Close

Ví dụ này mô tả một giao thức trong kiểu dữ liệu, và nó nói rõ nơi mà một thao tác có thể thất bại. Trong doorProg, kiểu của Open có nghĩa là bạn cần kiểm tra kết quả của nó trước khi có thể tiến hành với bất kỳ thao tác nào khác thay đổi trạng thái.

The type of Pure

Loại Pure trong DoorCmd cho phép bạn định nghĩa các hàm như sau, trong đó việc gọi Pure thay đổi trạng thái:

logOpen : DoorCmd DoorResult DoorClosed (\res => case res of OK => DoorOpen Jammed => DoorClosed) logOpen = do Display "Trying to open the door" OK <- Open | Jammed => do Display "Jammed" Pure Jammed Display "Success" Pure OK

Nếu bạn thay thế dòng cuối cùng, Pure OK, bằng một lỗ, ?pure_ok, bạn sẽ thấy rằng nó có trạng thái đầu vào là DoorOpen, và trạng thái đầu ra (của toàn bộ hàm logOpen) cần là một hàm tính toán trạng thái đầu ra của nó:

pure_ok : DoorCmd DoorResult DoorOpen (\res => case res of OK => DoorOpen Jammed => DoorClosed)

Loại Pure được thiết kế để hoạt động trong tình huống này:

Pure : (res : ty) -> DoorCmd ty (state_fn res) state_fn

Ở đây, state_fn là hàm chứa khối case, và Pure phải nhận OK như một đối số để có trạng thái đầu vào đúng cho ?pure_ok.

Bạn bây giờ đã có một định nghĩa của DoorCmd mô tả chính xác giao thức để mở và đóng cửa, nắm bắt khả năng xảy ra lỗi. Nhưng bạn chưa thấy cách mà hàm chạy tương ứng hoạt động, nơi mà kết quả của một thao tác Mở sẽ được sản xuất trong thực tế. Chúng ta sẽ xem xét điều này tiếp theo, trong bối cảnh của một ví dụ lớn hơn: một máy ATM. Chúng ta cũng sẽ xem xét cách mà trạng thái có thể thay đổi theo đầu vào của người dùng.

14.2. Security properties in types: modeling an ATM

Bạn có thể sử dụng các trạng thái rõ ràng trong các loại thao tác để đảm bảo, thông qua kiểm tra kiểu, rằng hệ thống chỉ thực hiện các thao tác quan trọng về an ninh khi ở trạng thái hợp lệ để làm như vậy. Ví dụ, một máy ATM chỉ nên phát tiền khi người dùng đã đưa thẻ vào và nhập đúng mã PIN. Đây là một chuỗi thao tác điển hình trên một máy ATM:

A user inserts their bank card.
The machine prompts the user for their PIN, to check that the user is entitled to use the card.
If PIN entry is successful, the machine prompts the user for an amount of money, and then dispenses cash.

Nếu người dùng nhập đúng mã PIN, máy sẽ được ở trạng thái sẵn sàng để rút tiền; ngược lại, nó sẽ không được như vậy. Trong phần này, chúng ta sẽ định nghĩa một mô hình cho ATM và xem cách thay đổi trạng thái của máy, dựa trên đầu vào của người dùng.

Security property of the ATM

Trong mô hình này, chúng tôi sẽ bỏ qua một số chi tiết nhỏ hơn của ngân hàng, chẳng hạn như truy cập và cập nhật tài khoản ngân hàng của người dùng, cũng như kiểm tra mã PIN một cách an toàn, điều này sẽ được thực hiện bằng các máy trạng thái riêng biệt. Chúng tôi sẽ tập trung vào một thuộc tính bảo mật quan trọng mà chúng tôi muốn duy trì: máy chỉ được phát tiền khi có thẻ hợp lệ trong máy.

Như với mô hình cửa, chúng ta sẽ bắt đầu bằng cách định nghĩa các trạng thái có thể của máy ATM và các thao tác có thể thay đổi trạng thái của máy ATM. Khi chúng ta biết cách các thao tác ảnh hưởng đến trạng thái, chúng ta có thể định nghĩa một kiểu dữ liệu để biểu diễn các thao tác trên máy.

14.2.1.
Defining states for the ATM

Một cây ATM đang chờ người dùng bắt đầu một tương tác, chờ người dùng nhập mã PIN, hoặc sẵn sàng phát tiền mặt sau khi xác thực mã PIN. Vì vậy, một cây ATM, trong mô hình của chúng tôi, có thể ở một trong các trạng thái sau:

Ready—The ATM is ready and waiting for a card to be inserted.
CardInserted—There is a card inside the ATM, but the system has not yet checked a PIN entry against the card.
Session—There is a card inside the ATM and the user has entered a valid PIN for the card, so a validated session is in progress.

Chúng tôi sẽ xác thực thẻ bằng cách kiểm tra xem người dùng nhập đúng mã PIN hay không. Trong máy bán hàng tự động ở chương 13, bạn cũng cần kiểm tra xem đầu vào có hợp lệ hay không, nhưng trong trường hợp đó, bạn có thể kiểm tra lệnh ở mức cục bộ. Ở đây, chúng tôi sẽ giả định rằng có một dịch vụ bên ngoài để kiểm tra mã PIN, vì vậy chúng tôi sẽ không biết cho đến khi chạy chương trình rằng đầu vào nào sẽ dẫn đến trạng thái nào.

Máy hỗ trợ các thao tác cơ bản sau, mỗi thao tác có thể có các điều kiện tiên quyết và điều kiện hậu quả trên trạng thái của máy:

InsertCard—Waits for a user to insert a card
EjectCard—Ejects a card from the machine, as long as there’s a card in the machine
GetPIN—Reads a user’s PIN, as long as there’s a card in the machine
CheckPIN—Checks whether an entered PIN is valid
Dispense—Dispenses cash as long as there’s a validated card in the machine
GetAmount—Reads from the user an amount to dispense
Message—Displays a message to the user

Hình 14.4 minh họa cách mà những thao tác này ảnh hưởng đến trạng thái của máy.

Figure 14.4.
A state machine describing the states and operations on an ATM. This omits operations (such as `GetAmount`) that are valid in all states.

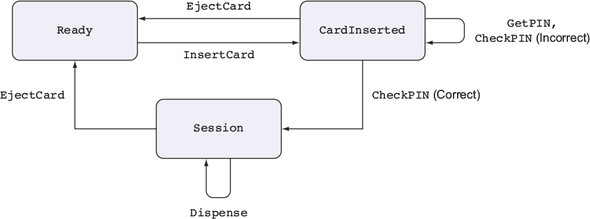
Sau khi đã xác định các trạng thái và xem cách mà các hoạt động cấp cao mà máy thực hiện có thể ảnh hưởng đến các trạng thái, chúng ta giờ đây có thể định nghĩa một loại cho ATM mô tả các chuyển tiếp trạng thái như mô tả trong hình 14.4.

14.2.2.
Defining a type for the ATM

Liệt kê 14.3 định nghĩa một kiểu ATMCmd đại diện cho các chuyển tiếp trạng thái của các thao tác trên một máy ATM bằng mã Idris. Nó cũng bao gồm GetAmount và Message, là hợp lệ trong mọi trạng thái và không ảnh hưởng đến trạng thái, cùng với các thao tác thông thường Pure và (>>=). Kiểu của EjectCard được đơn giản hóa một chút; chúng ta sẽ tinh chỉnh điều này trong phần 14.2.4.

Listing 14.3.
A type for representing the commands of an ATM, and how they affect the ATM’s state (ATM.idr)

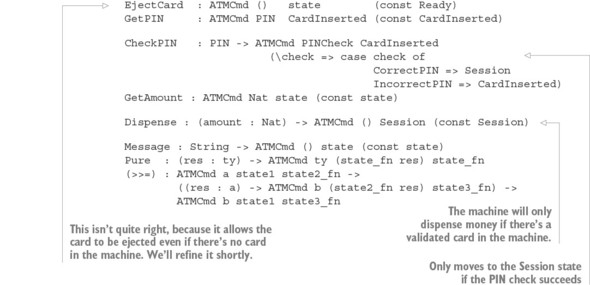
Sử dụng ATMCmd, bạn có thể viết một hàm mô tả một phiên giao dịch trên máy ATM, từ việc người dùng đưa thẻ vào đến việc máy phát tiền. Danh sách 14.4 cho thấy phần đầu của một hàm atm chờ người dùng đưa thẻ vào, yêu cầu mã PIN và sau đó kiểm tra kết quả. Tôi đã để lại một khoảng trống cho phần còn lại của chuỗi, trong đó chúng ta sẽ kiểm tra mã PIN và phát tiền nếu mã PIN hợp lệ.

Listing 14.4.
An `atm` function describing a sequence of operations on an ATM (ATM.idr)

Bạn có thể hoàn thành ATM như sau:

Type, define—If you check the type of the ?atm_rhs hole, you’ll see that you begin in a state that depends on the value of pinOK, and you need to end in the Ready state:

 pin : Vect 4 Char pinOK : PINCheck -------------------------------------- atm_rhs : ATMCmd () (case pinOK of CorrectPIN => Session IncorrectPIN => CardInserted) (\value => Ready)

The type here suggests you can proceed by checking the value of pinOK:

atm : ATMCmd () Ready (const Ready) atm = do InsertCard pin <- GetPIN pinOK <- CheckPIN pin case pinOK of CorrectPIN => ?atm_rhs_1 IncorrectPIN => ?atm_rhs_2

Type— If you check ?atm_rhs_1 and ?atm_rhs_2, you’ll see that the state is different in each case. In ?atm_rhs_1, the PIN was found to be valid, so you have a validated session:
```
 pinOK : PINCheck pin : Vect 4 Char -------------------------------------- atm_rhs_1 : ATMCmd () Session (\value => Ready)
```
In ?atm_rhs_2, on the other hand, the PIN was found to be invalid, so you’re still in the CardInserted state:
```
 pinOK : PINCheck pin : Vect 4 Char -------------------------------------- atm_rhs_2 : ATMCmd () CardInserted (\value => Ready)
```

Refine— In ?atm_rhs_1, you can now dispense cash, so you can prompt for an amount and dispense that:

case pinOK of CorrectPIN => do cash <- GetAmount Dispense cash ?atm_rhs_1 IncorrectPIN => ?atm_rhs_2

Type, refine—The input state of ?atm_rhs_1 is still Session, so before you finish you need to get back to the Ready state:

 pin : Vect 4 Char pinOK : PINCheck cash : Nat -------------------------------------- atm_rhs_1 : ATMCmd () Session (\value => Ready)

You can achieve this by ejecting the card:

case pinOK of CorrectPIN => do cash <- GetAmount Dispense cash EjectCard IncorrectPIN => ?atm_rhs_2

Refine— For ?atm_rhs_2, the PIN was invalid, so the simplest thing to do is eject the card, leading to the following completed definition:

atm : ATMCmd () Ready (const Ready) atm = do InsertCard pin <- GetPIN pinOK <- CheckPIN pin case pinOK of CorrectPIN => do cash <- GetAmount Dispense cash EjectCard IncorrectPIN => EjectCard

Có những cách khác mà bạn có thể định nghĩa máy rút tiền tự động (ATM). Ví dụ, sẽ rất hữu ích để hiển thị thông báo cho người dùng. Ngoài ra, trong thực tế, các máy ATM thường không kiểm tra mã PIN cho đến ngay trước khi phát tiền mặt. Liệt kê tiếp theo cho thấy cách triển khai máy ATM theo cách thay thế này.

Listing 14.5.
An alternative implementation of `atm`, including messages to the user and checking the PIN later (ATM.idr)

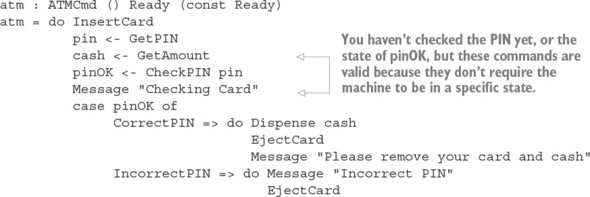
Miễn là bạn chỉ thực hiện các hành động khi máy ở trong trạng thái phù hợp, và miễn là bạn đảm bảo rằng mọi con đường thông qua các hành động trong ATM đều kết thúc ở trạng thái Sẵn sàng, bạn có thể triển khai các chi tiết theo cách bạn muốn. Nếu ATM đã được kiểm tra kiểu, bạn có thể chắc chắn rằng bạn đã duy trì thuộc tính bảo mật quan trọng: máy chỉ sẽ phát tiền khi có thẻ trong máy và mã PIN đã được nhập chính xác.

14.2.3.
Simulating an ATM at the console: executing ATMCmd

Để thử nghiệm chức năng ATM, bạn có thể viết một mô phỏng console của một cây ATM tạo ra các hành động IO cho một mô tả ATMCmd:

runATM : ATMCmd res inState outState_fn -> IO res

Cho một chuỗi ATMCmd tạo ra một kết quả có kiểu res, bắt đầu trong trạng thái inState, và tính toán trạng thái kết quả với outState_fn, runATM sẽ cung cấp một chuỗi hành động IO tạo ra một kết quả, res. Hãy mã hóa cứng một PIN hợp lệ duy nhất cho mô phỏng này:

testPIN : Vect 4 Char testPIN = ['1', '2', '3', '4']

Danh sách dưới đây hiển thị một mô phỏng bảng điều khiển của máy ATM sử dụng mã PIN được mã hóa sẵn này. Trong mô phỏng này, nhiều lệnh yêu cầu nhập liệu trên bảng điều khiển và trả về giá trị đã đọc.

Listing 14.6.
A console simulation of an ATM (ATM.idr)

Bạn đã định nghĩa máy ATM dưới dạng một loại, với các lệnh mô tả từng chuyển trạng thái trên máy ATM, và một hàm runATM riêng biệt để diễn giải những lệnh đó trong ngữ cảnh IO. Bằng cách tách biệt mô tả khỏi triển khai, bạn có thể viết các bộ diễn giải khác nhau cho các ngữ cảnh khác nhau, theo yêu cầu. Cụ thể, bạn không muốn mã hóa cứng một mã PIN trên một thiết bị thật!

14.2.4.
Refining preconditions using auto-implicits

Một đặc điểm của máy trạng thái trong hình 14.4 mà kiểu ATMCmd không hoàn toàn nắm bắt được là việc rút thẻ chỉ nên được phép khi có thẻ trong máy. Thay vào đó, bạn có kiểu sau:

EjectCard : ATMCmd () state (const Ready)

Có nghĩa là, bạn có thể thử tháo thẻ ở bất kỳ trạng thái nào, ngay cả khi không có thẻ trong máy. Nhưng chỉ có hai trạng thái khi việc tháo thẻ là hợp lệ: CardInserted và Session. Bạn không nên có thể viết hàm sau, vì máy đang tháo thẻ ở trạng thái Ready:

badATM : ATMCmd () Ready (const Ready) badATM = EjectCard

Bằng cách nào đó, bạn cần cả hai loại sau để làm việc với EjectCard:

EjectCard : ATMCmd () CardInserted (const Ready) EjectCard : ATMCmd () Session (const Ready)

Một bộ tạo dữ liệu như EjectCard không thể có hai loại khác nhau. Tuy nhiên, bạn có thể định nghĩa một predicate trên ATMState cho phép bạn hạn chế các trạng thái đầu vào có thể của EjectCard chỉ cho những trạng thái hợp lệ. Chúng ta đã thảo luận về predicate trong chương 9, và bạn có thể định nghĩa một predicate HasCard mô tả các trạng thái mà máy chứa thẻ:

data HasCard : ATMState -> Type where HasCI : HasCard CardInserted HasSession : HasCard Session

Bạn chỉ có thể xây dựng một giá trị của loại HasCard khi trạng thái là một trong hai trạng thái Card-Inserted hoặc Session, do đó bạn có thể tinh chỉnh loại của EjectCard như sau:

EjectCard : HasCard state -> ATMCmd () state (const Ready)

Nếu bạn làm điều này, bạn sẽ cần phải cung cấp các giá trị kiểu HasCard một cách rõ ràng khi sử dụng EjectCard. Ví dụ:

insertEject : ATMCmd () Ready (const Ready) insertEject = do InsertCard EjectCard HasCI

Việc phải viết các giá trị rõ ràng cho hàm đánh giá sẽ trở nên nhàm chán rất nhanh. Thay vào đó, bạn có thể sử dụng một hàm đánh giá tự động, điều mà bạn cũng đã thấy trong chương 9:

EjectCard : {auto prf : HasCard state} -> ATMCmd () state (const Ready)

Bây giờ, bạn có thể sử dụng EjectCard như trước, và để Idris tìm giá trị chính xác cho predicate bằng cách tìm kiếm qua các constructor dữ liệu có thể có cho HasCard để xem có bất kỳ constructor nào hợp lệ không:

insertEject : ATMCmd () Ready (const Ready) insertEject = do InsertCard EjectCard

Đối với badATM, Idris không nên có khả năng tìm thấy một giá trị phù hợp:

badATM : ATMCmd () Ready (const Ready) badATM = EjectCard

Trong trường hợp này, Idris sẽ báo lỗi, nói rằng nó cần tìm một giá trị kiểu HasCard Ready cho điều kiện EjectCard, nhưng không thể tìm thấy.

When checking argument prf to constructor Main.EjectCard: Can't find a value of type HasCard Ready

Tất cả các định nghĩa trước đây của bạn, bao gồm hai phiên bản của atm và hàm thực thi runATM, sẽ hoạt động mà không cần thay đổi gì với phiên bản tinh chế của EjectCard này.

Exercises

The following type outlines a security system in which a user can log in with a password and then read a secret message, although there are some gaps:

data Access = LoggedOut | LoggedIn data PwdCheck = Correct | Incorrect data ShellCmd : (ty : Type) -> Access -> (ty -> Access) -> Type where Password : String -> ShellCmd PwdCheck ?password_in ?password_out Logout : ShellCmd () ?logout_in ?logout_out GetSecret : ShellCmd String ?getsecret_in ?getsecret_out PutStr : String -> ShellCmd () state (const state) Pure : (res : ty) -> ShellCmd ty (state_fn res) state_fn (>>=) : ShellCmd a state1 state2_fn -> ((res : a) -> ShellCmd b (state2_fn res) state3_fn) -> ShellCmd b state1 state3_fn

Fill in the holes in the following types:

Password—Reads a password and changes the state to LoggedIn or LoggedOut, depending on whether the password was correct
Logout—Changes the state from LoggedIn to LoggedOut
GetSecret—Reads a secret message as long as the state is LoggedIn

The following function should type-check if you have the correct answer:

session : ShellCmd () LoggedOut (const LoggedOut) session = do Correct <- Password "wurzel" | Incorrect => PutStr "Wrong password" msg <- GetSecret PutStr ("Secret code: " ++ show msg ++ "\n") Logout

The following functions should not type-check:

sessionBad : ShellCmd () LoggedOut (const LoggedOut) sessionBad = do Password "wurzel" msg <- GetSecret PutStr ("Secret code: " ++ show msg ++ "\n") Logout noLogout : ShellCmd () LoggedOut (const LoggedOut) noLogout = do Correct <- Password "wurzel" | Incorrect => PutStr "Wrong password" msg <- GetSecret PutStr ("Secret code: " ++ show msg ++ "\n")

When inserting a coin into the vending machine defined in chapter 13, the machine could reject the coin. You can represent this by changing the types of MachineCmd and InsertCoin. An operation in MachineCmd can change the state based on its result:
```
data MachineCmd : (ty : Type) -> VendState -> (ty -> VendState) -> Type
```
Then, InsertCoin can return whether or not the coin insertion was successful and change the state accordingly:
```
InsertCoin : MachineCmd CoinResult (pounds, chocs) (\res => case res of Inserted => (S pounds, chocs) Rejected => (pounds, chocs))
```
Define the CoinResult type, and then make this change to MachineCmd in Vending .idr. Also, refine the types of the other commands and the implementation of machineLoop as necessary.

14.3. A verified guessing game: describing rules in types

Ví dụ kết thúc trong chương này, chúng ta sẽ xem cách bạn có thể sử dụng một kiểu để đại diện cho các quy tắc của một trò chơi một cách chính xác, và đảm bảo rằng bất kỳ triển khai nào của trò chơi đều tuân theo các quy tắc đúng. Chúng ta sẽ xem lại một ví dụ từ chương 9, trò chơi đoán chữ Hangman.

Để tóm tắt cách thức hoạt động này, bạn đã định nghĩa một loại WordState để đại diện cho trạng thái của trò chơi. WordState được định nghĩa như sau, bao gồm số lần đoán và số chữ cái còn lại như các tham số:

Bạn cũng đã định nghĩa một loại Finished để thể hiện khi một trò chơi hoàn thành, hoặc vì không còn chữ cái nào để đoán trong từ (nên người chơi đã thắng), hoặc vì không còn lần đoán nào (nên người chơi đã thua):

Dựa vào những điều này, bạn đã định nghĩa một vòng lặp chính gọi là game, vòng lặp này nhận một WordState với cả các dự đoán và chữ cái còn lại, và lặp cho đến khi trò chơi hoàn thành:

game : WordState (S guesses) (S letters) -> IO Finished

Trong việc triển khai, bạn đã sử dụng kiểu để giúp dẫn bạn đến một triển khai hoạt động. Nhưng bạn cũng có thể đã viết một triển khai không chính xác của trò chơi bằng cách sử dụng kiểu này. Ví dụ, triển khai sau đây của trò chơi cũng sẽ được gán kiểu tốt, nhưng sai, vì nó trả về trạng thái trò chơi thua ở tất cả các trường hợp:

game : WordState (S guesses) (S letters) -> IO Finished game state = pure (Lost (MkWordState "ANYTHING" ['A']))

Mặc dù kiểu dữ liệu cho phép bạn diễn đạt chính xác trạng thái trò chơi và giúp bạn gán kiểu cho các thao tác trung gian (chẳng hạn như xử lý một phỏng đoán), nhưng nó không đảm bảo rằng việc triển khai tuân theo đúng quy tắc của trò chơi. Trong triển khai trước đó, người chơi không thể thắng!

Trong phần này, thay vì định nghĩa một loại WordState và sau đó tin rằng game sẽ tuân theo các quy tắc của trò chơi một cách chính xác, chúng tôi sẽ định nghĩa các quy tắc của trò chơi một cách chính xác trong một loại trạng thái. Cũng như DoorCmd thể hiện khi nào chúng ta có thể thực hiện các thao tác trên một cánh cửa, và ATMCmd thể hiện khi nào chúng ta có thể thực hiện các thao tác trên một máy ATM, chúng ta có thể định nghĩa một loại GameCmd phụ thuộc, biểu thị khi nào việc thực hiện các thao tác cụ thể trong một trò chơi là hợp lệ, và tác động của những thao tác đó sẽ như thế nào. Tương tự như các ví dụ về cửa và ATM, chúng ta sẽ bắt đầu bằng cách định nghĩa các trạng thái và các thao tác có thể thực hiện trên các trạng thái đó.

14.3.1.
Defining an abstract game state and operations

Đầu tiên, chúng ta sẽ suy nghĩ về cách định nghĩa các quy tắc của trò chơi theo những cách trừu tượng, mà không lo lắng về chi tiết của việc triển khai. Một trò chơi có thể ở một trong các trạng thái sau:

NotRunning—There is no game currently in progress. Either the game hasn’t started and there’s no word yet to guess, or the game is complete.
Running—There is a game in progress, and the player has a number of guesses remaining and letters still to guess.

Trong trường hợp của Running, chúng tôi sẽ chú thích trạng thái với số lượng dự đoán và số chữ cái còn lại, giống như chúng tôi đã làm với WordState trước đó, vì điều này có nghĩa là chúng tôi sẽ có thể mô tả chính xác khi nào một trò chơi đã thắng (không còn chữ cái nào để đoán) hoặc thua (không còn lượt đoán). Chúng tôi có thể biểu thị các trạng thái khả thi trong kiểu dữ liệu sau:

data GameState : Type where NotRunning : GameState Running : (guesses : Nat) -> (letters : Nat) -> GameState

Sau đó, chúng tôi sẽ hỗ trợ một số thao tác cơ bản để thao tác với trạng thái trò chơi:

NewGame—Initializes a game with a word for the player to guess
Guess—Allows the player to guess a letter
Won—Declares that the player has won the game
Lost—Declares that the player has lost the game

Hình 14.5 minh họa cách mà các thao tác cơ bản này ảnh hưởng đến trạng thái trò chơi. Có thêm các điều kiện tiên quyết về Đã thắng và Đã thua: chúng ta chỉ có thể tuyên bố rằng người chơi đã thắng trò chơi nếu không còn chữ cái nào để đoán, và chúng ta chỉ có thể tuyên bố rằng người chơi đã thua nếu không còn lượt đoán nào.

Figure 14.5.
State transition diagram for Hangman. The `Running` state also holds the number of letters and guesses remaining. `Won` requires the number of letters to be zero, and `Lost` requires the number of guesses to be zero.

Bước tiếp theo là biểu diễn các trạng thái chuyển tiếp này một cách chính xác trong một kiểu phụ thuộc, bao gồm các quy tắc cụ thể về số lượng dự đoán và chữ cái cần thiết cho mỗi phép toán để hợp lệ.

14.3.2.
Defining a type for the game state

Chúng tôi sẽ định nghĩa một loại GameCmd mô tả các thao tác có thể thực hiện ảnh hưởng đến GameState.

Danh sách tiếp theo cho thấy các loại NewGame, Won và Lost từ hình 14.5. Như thường lệ, Pure và (>>=) được bao gồm để bạn có thể giới thiệu các giá trị thuần túy và các thao tác tuần tự.

Listing 14.7.
Beginning to define `GameCmd` (Hangman.idr)

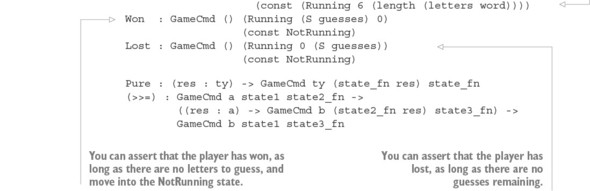
Bạn có thể lấy các chữ cái khác nhau trong một từ bằng cách sử dụng các chữ cái, sau đó chuyển đổi từ đó thành chữ in hoa, sau đó chuyển đổi nó thành một danh sách ký tự, và cuối cùng xóa bất kỳ phần tử trùng lặp nào:

Danh sách 14.8 thêm một phép đoán vào GameCmd. Kiểu của phép đoán có một điều kiện tiên quyết và một điều kiện hậu quả giải thích cách mà phép đoán ảnh hưởng đến trò chơi:

As a precondition, there must be at least one guess available (S guesses) and at least one letter still to guess (S letters), or attempting to guess a letter won’t type-check.
As a postcondition, the number of guesses will reduce if the guess was incorrect, and the number of letters will reduce if the guess was correct.

Listing 14.8.
Adding a `Guess` operation (Hangman.idr)

Cuối cùng, để có thể triển khai trò chơi với giao diện người dùng, bạn sẽ cần thêm các lệnh để hiển thị trạng thái trò chơi hiện tại, hiển thị bất kỳ tin nhắn nào và đọc một dự đoán từ người dùng:

data GameCmd : (ty : Type) -> GameState -> (ty -> GameState) -> Type where {- Continued from Listing 14.8 -} ShowState : GameCmd () state (const state) Message : String -> GameCmd () state (const state) ReadGuess : GameCmd Char state (const state)

Hiển thị trạng thái trò chơi nên hiển thị các chữ cái đã biết trong từ mục tiêu và số lần đoán còn lại. Ví dụ, nếu từ mục tiêu là TESTING và bạn đã đoán được chữ T, với sáu lần đoán còn lại, ShowState nên hiển thị như sau:

T--T--- 6 guesses left

Khi bạn thực sự triển khai trò chơi, việc hỗ trợ các vòng lặp trò chơi kéo dài vô thời hạn là rất hữu ích. Ví dụ, khi một người chơi kết thúc một trò chơi, họ có thể muốn bắt đầu một trò chơi mới. Danh sách tiếp theo định nghĩa một loại GameLoop, sử dụng Inf để ghi chú rằng việc thực thi có thể tiếp tục vô hạn.

Listing 14.9.
A type for describing potentially infinite game loops (Hangman.idr)

Bạn có thể sử dụng các phép toán trong GameLoop và GameCmd để định nghĩa hàm sau, hàm này triển khai một vòng lặp trò chơi:

gameLoop : GameLoop () (Running (S guesses) (S letters)) (const NotRunning)

Khi bạn có một cài đặt gameLoop được gõ đúng và đầy đủ, bạn sẽ biết rằng đó là một cài đặt hợp lệ của các quy tắc. Cả trò chơi và người chơi sẽ không thể gian lận bằng cách phá vỡ các quy tắc như được định nghĩa trong GameCmd. Bạn chỉ có thể gọi gameLoop trên một trò chơi được khởi tạo đúng cách, với một từ cần đoán, và bất kỳ cài đặt nào cũng phải là một cài đặt hoàn chỉnh của trò chơi vì cách duy nhất để kết thúc một GameLoop là gọi Exit, điều này yêu cầu trò chơi phải ở trạng thái NotRunning.

14.3.3.
Implementing the game

Chúng tôi sẽ triển khai gameLoop một cách tương tác và xem trạng thái của trò chơi tiến triển như thế nào bằng cách kiểm tra các loại khi chúng tôi tiến hành.

Để bắt đầu, bạn có thể tạo một định nghĩa khung, đưa các dự đoán và chữ cái từ loại vào phạm vi, vì bạn sẽ cần kiểm tra chúng để xem tiến trình của người chơi sau này.

gameLoop : GameLoop () (Running (S guesses) (S letters)) (const NotRunning) gameLoop {guesses} {letters} = ?gameLoop_rhs

Để triển khai gameLoop, hãy thực hiện các bước sau:

Refine— At the start of each iteration of gameLoop, you’ll display the current state of the game using ShowState, read a guess from the user, and then check whether it was correct:
```
gameLoop : GameLoop () (Running (S guesses) (S letters)) (const NotRunning) gameLoop {guesses} {letters} = do ShowState g <- ReadGuess ok <- Guess g ?gameLoop_rhs
```

Type, define—If you check the type of ?gameLoop_rhs now, you’ll see that the current state of the game depends on whether the guess was correct or not:

 letters : Nat guesses : Nat g : Char ok : GuessResult -------------------------------------- gameLoop_rhs : GameLoop () (case ok of Correct => Running (S guesses) letters Incorrect => Running guesses (S letters)) (\value => NotRunning)

To make progress, you’ll need to inspect ok to establish which state the game is in:

gameLoop : GameLoop () (Running (S guesses) (S letters)) (const NotRunning) gameLoop {guesses} {letters} = do ShowState g <- ReadGuess ok <- Guess g case ok of Correct => ?gameLoop_rhs_1 Incorrect => ?gameLoop_rhs_2

Type, define—In ?gameLoop_rhs_1, the guess was correct, so the number of letters remaining is reduced, as you can see by checking its type:
```
 ok : GuessResult letters : Nat guesses : Nat g : Char -------------------------------------- gameLoop_rhs_1 : GameLoop () (Running (S guesses) letters) (\value => NotRunning)
```
You can only continue with gameLoop if there are both letters and guesses remaining, because its input state is Running (S guesses) (S letters). To decide how to continue, you’ll need to check the current value of letters:
```
case ok of Correct => case letters of Z => ?gameLoop_rhs_3 S k => ?gameLoop_rhs_4 Incorrect => ?gameLoop_rhs_2
```
Refine— In ?gameLoop_rhs_3, there are no letters left to guess, so the player has won. You can declare that the player has won with Won, moving to the Not-Running state. Then display the final state and exit:
```
case ok of Correct => case letters of Z => do Won ShowState Exit S k => ?gameLoop_rhs_4 Incorrect => ?gameLoop_rhs_2
```
You need to Exit explicitly, because Exit is the only way to break out of a GameLoop. You can only Exit a game in the NotRunning state.

Refine— In ?gameLoop_rhs_4, there are still letters to guess, so you can display a message and continue with gameLoop:

case ok of Correct => case letters of Z => do Won ShowState Exit S k => do Message "Correct" gameLoop Incorrect => ?gameLoop_rhs_2

Trường hợp không đúng hoạt động tương tự, kiểm tra xem có còn lượt đoán hay không và tuyên bố rằng người chơi đã thua nếu không còn. Danh sách dưới đây cung cấp định nghĩa đầy đủ, để tham khảo.

Listing 14.10.
A complete implementation of `gameLoop` (Hangman.idr)

gameLoop : GameLoop () (Running (S guesses) (S letters)) (const NotRunning) gameLoop {guesses} {letters} = do ShowState g <- ReadGuess ok <- Guess g case ok of Correct => case letters of Z => do Won ShowState Exit S k => do Message "Correct" gameLoop Incorrect => case guesses of Z => do Lost ShowState Exit (S k) => do Message "Incorrect" gameLoop

Bạn cũng cần khởi tạo trò chơi. Ví dụ, bạn có thể viết một hàm để thiết lập một trò chơi mới, sau đó khởi động gameLoop:

hangman : GameLoop () NotRunning (const NotRunning) hangman = do NewGame "testing" gameLoop

Cho đến nay, bạn chỉ mới định nghĩa một kiểu dữ liệu mô tả các hành động trong trò chơi. Hàm gameLoop mô tả các chuỗi hành động trong một trò chơi Hangman hợp lệ theo quy tắc. Để chạy trò chơi, bạn sẽ cần định nghĩa một đại diện cụ thể của trạng thái trò chơi và một hàm chuyển đổi một GameLoop thành một chuỗi các hành động IO.

14.3.4.
Defining a concrete game state

Trong ví dụ về ngăn xếp ở chương 13, chúng ta có một trạng thái trừu tượng của ngăn xếp (số lượng mục trên ngăn xếp), và một trạng thái cụ thể được đại diện bởi một mảng Vect có độ dài phù hợp. Tương tự, GameState là trạng thái trừu tượng của một trò chơi, chỉ mô tả liệu trò chơi có đang diễn ra hay không, và nếu có, thì còn lại bao nhiêu lần đoán và có bao nhiêu chữ cái.

Để chạy một trò chơi, bạn cần xác định một trạng thái trò chơi cụ thể tương ứng, bao gồm từ mục tiêu cụ thể và những chữ cái nào vẫn cần được đoán. Danh sách sau đây định nghĩa một loại trò chơi với một đối số GameState, đại diện cho dữ liệu cụ thể liên quan đến một trạng thái trò chơi trừu tượng.

Listing 14.11.
Representing the concrete game state (Hangman.idr)

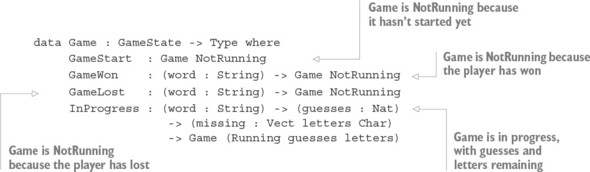
Thật tiện lợi khi định nghĩa một triển khai Show cho Game để bạn có thể dễ dàng hiển thị một đại diện chuỗi về tiến trình của trò chơi.

Listing 14.12.
A `Show` implementation for `Game` (Hangman.idr)

Bạn có thể sử dụng Game để theo dõi trạng thái trò chơi cụ thể. Khi bạn thực hiện một GameLoop, bạn sẽ lấy trạng thái trò chơi cụ thể làm đầu vào và trả về một kết quả cùng với trạng thái trò chơi đã được cập nhật:

Bạn sử dụng Fuel, vì nó có khả năng chạy các vòng lặp. Cụ thể, khi bạn đọc một Giả định từ người chơi, đầu vào hợp lệ duy nhất là một ký tự chữ cái đơn, vì vậy bạn sẽ cần tiếp tục yêu cầu nhập cho đến khi nó hợp lệ.

Nếu bạn hết nhiên liệu, GameResult cần nói rằng việc thực hiện đã thất bại. Ngược lại, nó cần lưu trữ kết quả của hoạt động và trạng thái mới. Quan trọng là, loại của trạng thái mới có thể phụ thuộc vào kết quả; ví dụ, số lần đoán khả dụng khác nhau tùy thuộc vào việc Guess trả về Đúng hay Sai. Do đó, một GameResult là một trong những điều sau:

A pair of the result produced by executing the game and the output state, with a type calculated from the result
An error, if run ran out of fuel

Bạn có thể định nghĩa GameResult như sau:

`outstate_fn được bao gồm trong kiểu GameResult vì như vậy bạn sẽ rõ ràng trong kiểu về cách bạn đang tính toán trạng thái đầu ra của Game.`

Bây giờ bạn đã có một kiểu dữ liệu để đại diện cho trạng thái cụ thể của một trò chơi—mà nhận trạng thái trừu tượng làm đối số—cùng với một đại diện cho kết quả, bạn đã sẵn sàng để triển khai hàm run.

14.3.5.
Running the game: executing GameLoop

Danh sách tiếp theo phác thảo định nghĩa của hàm run cho GameLoop. Hàm này sử dụng một hàm khác, runCmd, để thực thi GameCmd. Hiện tại, vẫn còn thiếu định nghĩa của hàm runCmd.

Listing 14.13.
Running the game loop (Hangman.idr)

Trong quá trình thực thi, khi thành công, bạn sử dụng pure để trả về một cặp kết quả và trạng thái mới. Bởi vì bạn sẽ thường trả về kết quả theo hình thức này khi thực thi một lệnh, bạn có thể định nghĩa một hàm trợ giúp, ok, để làm cho điều này ngắn gọn hơn:

ok : (res : ty) -> Game (outstate_fn res) -> IO (GameResult ty outstate_fn) ok res st = pure (OK res st)

Sử dụng ok, bạn có thể tinh chỉnh điều khoản cuối cùng của run thành như sau:

run (More fuel) st Exit = ok () st

Danh sách 14.14 cung cấp một định nghĩa phác thảo của runCmd, để lại các chỗ trống cho các trường hợp Guess và ReadGuess. Trong các trường hợp khác, bạn sử dụng ok để cập nhật trạng thái theo yêu cầu của kiểu và thực hiện các hành động IO khi cần thiết.

Listing 14.14.
Outline definition of `runCmd` (Hangman.idr)

Khi một trò chơi đang diễn ra, trạng thái trò chơi sử dụng bộ khởi tạo InProgress của Game, có kiểu sau:

*Hangman> :t InProgress InProgress : String -> (guesses : Nat) -> Vect letters Char -> Game (Running guesses letters)

Tham số thứ ba là một vector các chữ cái vẫn chưa được đoán. Vì vậy, trong trường hợp đoán, bạn kiểm tra xem ký tự đã đoán có nằm trong vector các chữ cái còn thiếu hay không:

Bạn đã định nghĩa removeElem một cách tương tác trong chương 9 của phiên bản trước của trò chơi Hangman. Để tiện lợi, tôi sẽ lặp lại ở đây:

removeElem : (value : a) -> (xs : Vect (S n) a) -> {auto prf : Elem value xs} -> Vect n a removeElem value (value :: ys) {prf = Here} = ys removeElem {n = Z} value (y :: []) {prf = There later} = absurd later removeElem {n = (S k)} value (y :: ys) {prf = There later} = y :: removeElem value ys

Cuối cùng, bạn cần định nghĩa trường hợp ReadGuess, trường hợp này đọc một ký tự từ người chơi. Đầu vào chỉ hợp lệ nếu đó là một ký tự chữ cái, vì vậy bạn sẽ lặp lại cho đến khi người chơi nhập một đầu vào hợp lệ:

Trường hợp này có thể lặp vô hạn nếu người dùng cứ tiếp tục nhập vào dữ liệu không hợp lệ, vì vậy runCmd nhận Fuel làm tham số và tiêu tốn nhiên liệu mỗi khi có đầu vào không hợp lệ. Kết quả là runCmd vẫn hoàn toàn vì nó hoặc tiêu tốn nhiên liệu hoặc xử lý một lệnh trong mỗi cuộc gọi đệ quy. Điều quan trọng là runCmd phải hoàn toàn, vì điều đó có nghĩa là bạn biết rằng việc thực thi một GameCmd sẽ tiếp tục tiến triển miễn là còn có các lệnh để thực thi.

Bạn đang ở trong vị trí để viết chương trình chính, sử dụng forever để đảm bảo rằng, trong thực tế, run sẽ không bao giờ hết nhiên liệu. Hãy thêm đoạn sau vào cuối Hangman.idr:

Bạn bây giờ có thể thực thi trò chơi tại REPL. Dưới đây là một ví dụ:

*Hangman> :exec ------- 6 guesses left Guess: t Correct T--T--- 6 guesses left Guess: x Incorrect T--T--- 5 guesses left Guess: g Correct T--T--G 5 guesses left Guess: bad Invalid input Guess:

Trong ví dụ này, chúng tôi đã tách riêng phần mô tả các quy tắc, trong GameCmd và GameLoop, khỏi việc thực thi các quy tắc, trong runCmd và run. Về cơ bản, GameCmd và GameLoop định nghĩa một giao diện để xây dựng một trò chơi Hangman hợp lệ, đúng theo các quy tắc. Bất kỳ hàm tổng quát nào có kiểu định nghĩa đúng sử dụng các kiểu này phải là một triển khai chính xác của các quy tắc, nếu không nó sẽ không được kiểm tra kiểu!

14.4. Summary

You can get feedback from the environment by using the result of an operation to compute the output state of a command.
A system might be in a different state after running a command, depending on whether the command was successful.
Defining preconditions on operations allows you to express security properties in types, such as when it’s valid for an ATM to dispense cash.
A system might change state according to whether a user’s input is valid in the current environment, such as whether a PIN or password is correct.
Predicates and auto implicits help you describe valid input states of operations precisely.
You can describe the rules of a game precisely in a type, so that a function that type-checks must be a valid implementation of the rules.
You use an abstract state type to describe what operations do, and a concrete state, depending on the abstract state, to describe their corresponding implementations.

Chapter 15.
Type-safe concurrent programming

Chương này đề cập đến

Using concurrency primitives
Defining a type for describing concurrent processes
Using types to ensure concurrent processes communicate consistently

Trong Idris, một giá trị của loại IO () mô tả một chuỗi hành động để tương tác với người dùng và hệ điều hành, mà hệ thống thời gian chạy thực hiện tuần tự. Nghĩa là, nó chỉ thực hiện một hành động tại một thời điểm. Bạn có thể gọi một chuỗi các hành động tương tác là một tiến trình.

Cũng như thực hiện các hành động theo tuần tự trong một quy trình duy nhất, thường rất hữu ích khi có thể thực hiện nhiều quy trình đồng thời và cho phép các quy trình đó giao tiếp với nhau. Trong chương này, tôi sẽ giới thiệu lập trình đồng thời trong Idris.

Message passing

Lập trình đồng thời là một chủ đề lớn, và có nhiều cách tiếp cận khác nhau mà mỗi cách có thể làm đầy một cuốn sách riêng. Chúng ta sẽ xem xét một số ví dụ nhỏ về tính đồng thời dựa trên truyền thông điệp, nơi các tiến trình tương tác với nhau bằng cách gửi tin nhắn. Truyền thông điệp được hỗ trợ như một nguyên thủy bởi hệ thống chạy Idris. Trên thực tế, việc gửi một tin nhắn đến một tiến trình và nhận phản hồi tương ứng với việc gọi một phương thức trả về kết quả trong một ngôn ngữ hướng đối tượng.

Lập trình đồng thời có nhiều lợi thế:

You can continue to interact with a user while a large computation runs. For example, a user can continue browsing a web page while a large file downloads.
You can display feedback on the progress of a large computation running in another process, such as displaying a progress bar for a download.
You can take full advantage of the processing power of modern CPUs, dividing work between multiple processes running on separate CPU cores.

Chương này trình bày một ví dụ lớn hơn về phát triển dựa trên kiểu. Đầu tiên, tôi sẽ giới thiệu các kiểu nguyên thủy cho lập trình đồng thời trong Idris và mô tả những vấn đề có thể xảy ra trong quá trình đồng thời nói chung. Sau đó, tôi sẽ trình bày một nỗ lực ban đầu về một kiểu để mô tả các quá trình đồng thời. Nỗ lực ban đầu này sẽ có một số thiếu sót, vì vậy chúng ta sẽ tinh chỉnh nó và đạt được một kiểu cho phép các quá trình giao tiếp với nhau một cách an toàn và nhất quán.

15.1. Primitives for concurrent programming in Idris

Thư viện cơ sở Idris cung cấp một mô-đun, System.Concurrency.Channels, bao gồm các nguyên thủy để khởi động các tiến trình đồng thời và cho phép các tiến trình này giao tiếp với nhau. Điều này cho phép bạn, về lý thuyết, viết các ứng dụng sử dụng hiệu quả CPU của bạn và vẫn duy trì tính phản hồi ngay cả khi thực hiện các phép tính phức tạp.

Tuy nhiên, bất chấp những ưu điểm của nó, lập trình đồng thời nổi tiếng là dễ mắc lỗi. Nhu cầu cho nhiều tiến trình tương tác với nhau làm tăng đáng kể độ phức tạp của một chương trình. Ví dụ, nếu bạn đang hiển thị thanh tiến trình trong khi một tệp đang được tải về, tiến trình tải tệp cần phối hợp với tiến trình hiển thị thanh tiến trình để biết được đã tải về bao nhiêu tệp. Độ phức tạp này dẫn đến những cách mới mà các chương trình có thể thất bại trong thời gian chạy:

Deadlock— Two or more processes are waiting for each other to perform some action before they can continue.
Race conditions— The behavior of a system depends on the ordering of actions in multiple concurrent processes.

Hệ quả của tình huống deadlock là các tiến trình liên quan bị đứng yên, không còn chấp nhận đầu vào hoặc cho ra đầu ra. Hai tiến trình đồng thời - hãy gọi chúng là client và server - có thể rơi vào tình trạng deadlock nếu client đang chờ nhận một tin nhắn từ server trong khi server cũng đang chờ nhận một tin nhắn từ client. Nếu điều này xảy ra, cả client và server sẽ đứng yên.

Cac điều kiện đua có thể khó xác định hơn. Đoạn mã giả trong hình 15.1 cho client và server minh họa một điều kiện đua, nơi giá trị của biến chia sẻ var phụ thuộc vào thứ tự mà các thao tác đồng thời được thực hiện. Chúng ta sẽ giả định rằng các thao tác Đọc và Ghi lần lượt đọc và ghi giá trị của một biến có thể thay đổi được chia sẻ, vì vậy Đọc var đọc giá trị của biến chia sẻ var.

Figure 15.1.
Pseudocode for `client` and `server`, in which each process reads and writes a shared variable, `var`. This could lead to an unexpected result if lines A and C are executed before lines C and D.

Ở đây, khách hàng và máy chủ thực thi song song, và giá trị cuối cùng của biến tùy thuộc vào thứ tự mà các thao tác A, B, C và D được thực thi. A sẽ luôn chạy trước B, và C trước D, nhưng mặt khác có sáu cách sắp xếp khả thi cho các thao tác. Bảng 15.1 liệt kê các cách sắp xếp này và giá trị kết quả của biến trong mỗi trường hợp, giả sử giá trị ban đầu là 1.

Table 15.1.
Value of `var` for each sequence of operations in figure 15.1, given an initial value of `1` for `var`

Lệnh tác chiến	Giá trị của biến
A, B, C, D	3
A, C, B, D	2
A, C, D, B	2
C, A, B, D	2
C, A, D, B	2
C, D, A, B	3

Như bảng cho thấy, với giá trị ban đầu của biến là 1, có hai kết quả khả thi cho biến, tùy thuộc vào thứ tự mà các thao tác Đọc và Ghi được thực hiện. Ở đây, chỉ có hai tiến trình với hai thao tác mỗi tiến trình. Khi các chương trình phát triển, khả năng xảy ra kết quả không xác định kiểu này trở nên lớn hơn rất nhiều.

Sau này trong chương này, bằng cách sử dụng nhiều kỹ thuật mà chúng ta đã thảo luận trước đó trong cuốn sách này, bạn sẽ thấy cách viết các chương trình đồng thời trong Idris, tránh những vấn đề như tình trạng chết (deadlock) và điều kiện đua (race conditions). Nhưng trước tiên, bạn cần hiểu các nguyên thủy mà thư viện cơ sở của Idris cung cấp cho lập trình đồng thời và xem những loại vấn đề bạn sẽ gặp phải khi viết các quy trình cần phải phối hợp với nhau.

15.1.1.
Defining concurrent processes

Trong một chương trình Idris hoàn chỉnh, hàm chính, có kiểu IO (), mô tả các hành động mà hệ thống thời gian chạy sẽ thực hiện khi chương trình được chạy. Do đó, hàm chính mô tả các hành động được thực hiện trong một tiến trình duy nhất.

Các hành động mà chúng tôi đã sử dụng mô tả các hoạt động I/O trên console và file, nhưng hệ thống runtime cũng hỗ trợ các hành động để khởi động các quy trình mới và gửi tin nhắn giữa các quy trình. Có các phép toán nguyên thủy cho các hành động sau:

Creating a new process. Each process is associated with a unique process identifier (PID).
Sending a message to a process identified by its PID.
Receiving a message from another process.

Hình 15.2 minh họa một cách mà chúng ta có thể sử dụng truyền tin nhắn để viết các quy trình đồng thời giao tiếp với nhau. Trong hình này, main và adder là hai quy trình Idris, chạy đồng thời, trong đó mỗi quy trình có thể gửi tin nhắn cho quy trình kia.

Figure 15.2.
Message-passing between processes. A `main` process sends an `Add 2 3` message to an `adder` process, which replies by sending a `5` message back to `main`.

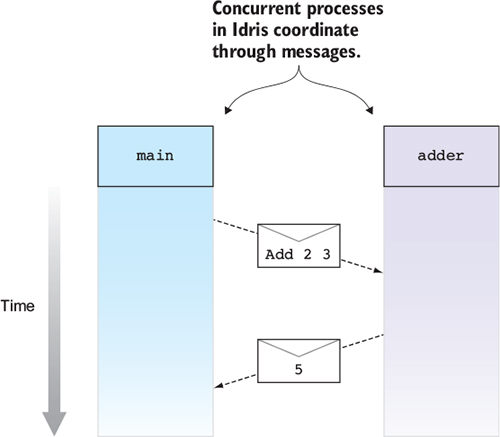
Tin nhắn mà main gửi đến adder sử dụng định dạng sau:

data Message = Add Nat Nat

Trong ví dụ này, sau khi main gửi thông điệp "Thêm 2 3" đến quá trình cộng, nó mong đợi nhận được phản hồi với kết quả của phép cộng 2 và 3. Bằng cách này, bạn có thể sử dụng các quá trình chạy đồng thời để triển khai các dịch vụ phản hồi các yêu cầu được gửi bởi các quá trình khác. Ở đây, chúng ta có một dịch vụ thực hiện phép cộng, chạy trong một quá trình riêng biệt.

Tôi sẽ sử dụng điều này như một ví dụ liên tục về các quá trình đồng thời. Tiếp theo, bạn sẽ thấy cách sử dụng các nguyên tố đồng thời mà Idris cung cấp để triển khai một dịch vụ cộng trong một quá trình riêng biệt, và cách sử dụng dịch vụ đó từ main.

15.1.2.
The Channels library: primitive message passing

Mô-đun System.Concurrency.Channels, trong thư viện cơ sở, định nghĩa các kiểu dữ liệu và hành động cho phép các quá trình Idris tạo ra các quá trình mới và giao tiếp với nhau. Nó định nghĩa các kiểu sau:

PID—Represents a process identifier. Every process is associated with a PID that allows you to set up a communication channel with the process.
Channel—A link between two processes. It defines a communication channel along which you can send messages.

Mô-đun System.Concurrency.Channels cũng định nghĩa các hàm sau đây để tạo ra quy trình mới và thiết lập các kênh giao tiếp:

spawn—Creates a new process for executing a sequence of actions of type IO (), and if successful returns its PID.
connect—Initiates a communication channel to a running process.
listen—Waits for another process to initiate a communication. When another process connects, it sets up a communication channel with that process.

Cuối cùng, mô-đun định nghĩa các thao tác để gửi và nhận tin nhắn trên một Kênh. Chúng ta sẽ xem xét định nghĩa kiểu trong System.Concurrency.Channels ngay sau đây, nhưng trước tiên hãy xem cách các quá trình và kênh được thiết lập cho các quá trình chính và cộng. Quá trình chính hoạt động như sau:

Starts the adder process using spawn
Sets up a communication channel to adder using connect
Sends an Add 2 3 message on the channel
Receives a reply on the channel with the result

Tương ứng, quá trình cộng sẽ hoạt động như sau:

Waits for another process to initiate a communication using listen and sets up a new communication channel when another process connects
Receives a message on the channel containing the numbers to be added
Sends a message on the channel with the result
Returns to step 1, waiting for the next request

Quá trình adder cung cấp một dịch vụ lâu dài chờ đợi các yêu cầu đến và gửi phản hồi cho những yêu cầu đó. Một khi main đã khởi động quá trình adder, bất kỳ quá trình nào khác cũng có thể gửi yêu cầu đến adder, miễn là nó biết PID của adder.

Danh sách đầu tiên hiển thị các khai báo kiểu cho các kênh và PID trong System.Concurrency.Channels cũng như các hàm mà bạn có thể sử dụng để tạo quy trình và thiết lập các kênh truyền thông.

Listing 15.1.
Channels and PIDs (defined in `System.Concurrency.Channels`)

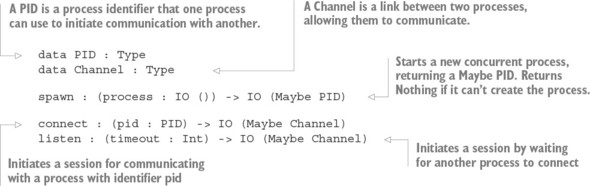
Khi bạn lắng nghe một kết nối hoặc kết nối đến một quá trình khác, không có gì đảm bảo rằng bạn sẽ thành công trong việc thiết lập một kênh giao tiếp. Có thể không có kết nối nào đến, hoặc quá trình mà bạn đang kết nối có thể không còn hoạt động nữa. Vì vậy, để ghi lại khả năng thất bại, các hàm connect và listen trả về một giá trị có kiểu Maybe Channel.

Bạn có thể sử dụng spawn, listen và connect để thiết lập adder và main như hai quá trình tách biệt. Danh sách sau đây phác thảo một chương trình thiết lập các quá trình, để lại khoảng trống cho các phần của quá trình gửi tin nhắn cho nhau.

Listing 15.2.
Outline of a program that sets up an `adder` process (AdderChannel.idr)

Bây giờ bạn đã thiết lập các quy trình và kênh, main có thể gửi tin nhắn cho adder, và adder có thể trả lời. Bạn có thể sử dụng các nguyên tắc sau:

unsafeSend—Sends a message of any type
unsafeRecv—Receives a message of an expected type

Như các tên gọi đã chỉ ra, các nguyên thủy này không an toàn, vì chúng không cung cấp cách để kiểm tra rằng người gửi và người nhận đang mong đợi các tin nhắn được gửi theo một thứ tự cụ thể, hoặc rằng họ đang gửi và nhận các tin nhắn của các loại nhất quán. Tuy nhiên, tạm thời chúng ta sẽ sử dụng chúng để hoàn thành việc triển khai main và adder. Sau này, trong phần 15.2, bạn sẽ thấy cách để tạo ra các phiên bản an toàn đảm bảo rằng các quá trình gửi và nhận tin nhắn theo một giao thức nhất quán.

Why support an unsafe Channel type?

Có thể bạn sẽ ngạc nhiên khi biết rằng Idris, một ngôn ngữ được thiết kế để hỗ trợ phát triển dựa trên kiểu, lại hỗ trợ các nguyên thủy đồng thời không an toàn như vậy thay vì những thứ tinh vi hơn. Lý do là có nhiều phương pháp có thể để triển khai các chương trình đồng thời an toàn theo cách dựa trên kiểu, và bằng cách cung cấp các nguyên thủy cơ bản không an toàn, Idris không bị giới hạn chỉ ở một trong số đó. Bạn sẽ thấy một phương pháp như vậy ngay sau đây.

Danh sách dưới đây hiển thị các khai báo kiểu cho những phép toán nguyên thủy này, được định nghĩa trong System.Concurrency.Channels.

Listing 15.3.
Primitive message passing (defined in `System.Concurrency.Channels`)

unsafeSend : Channel -> (val : a) -> IO Bool unsafeRecv : (expected : Type) -> Channel -> IO (Maybe expected)

Trong danh sách tiếp theo, bạn có thể hoàn thành định nghĩa của phép cộng bằng cách nhận yêu cầu từ người gửi và sau đó gửi phản hồi. Với unsafeRecv, bạn khẳng định rằng yêu cầu có kiểu là Message.

Listing 15.4.
Complete definition of `adder` (AdderChannel.idr)

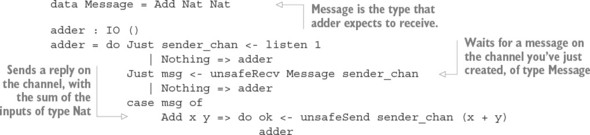
Tương tự, danh sách dưới đây cho thấy định nghĩa hoàn chỉnh của hàm main, gửi một thông điệp bằng unsafeSend và nhận một phản hồi có kiểu Nat bằng unsafeRecv.

Listing 15.5.
Complete definition of `main` (AdderChannel.idr)

Nếu bạn biên dịch và thực thi main bằng :exec tại REPL, bạn sẽ thấy rằng nó nhận được kết quả 5 từ adder:

*AdderChannel> :exec main 5

Điều này chỉ hoạt động vì bạn đã đảm bảo rằng main và adder đồng ý với một mẫu giao tiếp. Khi main gửi một thông điệp qua một kênh, quá trình adder đang mong đợi nhận một thông điệp trên kênh tương ứng của nó, và ngược lại.

15.1.3.
Problems with channels: type errors and blocking

Kênh cung cấp một phương pháp cơ bản để thiết lập liên kết giữa các tiến trình và gửi tin nhắn qua các liên kết đó. Tuy nhiên, các loại unsafeSend và unsafeRecv không cung cấp bất kỳ đảm bảo nào về cách mà các tiến trình phối hợp với nhau. Do đó, rất dễ mắc phải sai lầm.

Ví dụ, adder gửi một Nat để phản hồi lại main, nhưng nếu main đang mong đợi nhận một String thì sao?

Trong trường hợp này, việc thực thi hàm main sẽ hoạt động một cách không dự đoán được, và rất có thể sẽ gặp sự cố, bởi vì trong thời gian chạy có sự không nhất quán giữa kiểu của thông điệp nhận được và kiểu mong đợi. Không có điều gì trong các kiểu của unsafeSend và unsafeRecv giải thích cách mà việc gửi và nhận được phối hợp giữa hai quá trình, vì vậy Idris sẵn sàng chấp nhận main là hợp lệ mặc dù sự phối hợp này, trong trường hợp này, là không đúng.

Một vấn đề khác xảy ra nếu các thao tác unsafeSend và unsafeReceive không tương ứng trong mỗi quy trình. Ví dụ, main có thể gửi một tin nhắn thứ hai trên cùng một kênh và mong đợi một phản hồi:

Mặc dù đoạn mã này kiểm tra loại thành công, khi bạn cố gắng thực thi nó, nó sẽ in phản hồi đầu tiên từ adder nhưng bị chặn khi chờ phản hồi thứ hai. Sau khi adder tạo kênh bằng cách lắng nghe, nó chỉ trả lời một tin nhắn trên kênh đó.

Mặc dù các kênh tự chúng không an toàn, bạn có thể sử dụng chúng như một cấu trúc cơ bản để định nghĩa giao tiếp an toàn theo kiểu. Chúng ta sẽ định nghĩa một kiểu để mô tả sự phối hợp giữa các quá trình giao tiếp, và sau đó viết một hàm chạy để thực thi mô tả đó bằng cách sử dụng các cấu trúc không an toàn. Dù cuối cùng bạn sẽ cần phải sử dụng các cấu trúc đó, nhưng bạn có thể đóng gói tất cả các chi tiết trong một kiểu duy nhất, mang tính mô tả mà bạn có thể sử dụng để phát triển hệ thống giao tiếp theo hướng kiểu.

15.2. Defining a type for safe message passing

Trong hệ thống thời gian chạy Idris, các quá trình đồng thời hoạt động độc lập với nhau. Không có bộ nhớ chia sẻ, và cách duy nhất mà các quá trình có thể giao tiếp với nhau là thông qua việc gửi tin nhắn cho nhau. Bởi vì không có bộ nhớ chia sẻ, không có các điều kiện đua do truy cập vào trạng thái chia sẻ đồng thời, nhưng có một số vấn đề khác cần xem xét:

How can you ensure that the type of the message that main sends is the same type that adder expects to receive?
What happens if main sends a message to adder, but adder doesn’t reply?
What happens if adder has stopped running when main sends a message?
How can you prevent the situation where main and adder are both waiting for a message from each other?

Trong phần này, bạn sẽ thấy cách giải quyết các vấn đề này bằng cách định nghĩa một kiểu Quy trình, cho phép bạn mô tả các quy trình giao tiếp có kiểu dữ liệu đúng.

Types and concurrent programming

Hỗ trợ cho các kiểu trong lập trình đồng thời thường khá hạn chế trong các ngôn ngữ lập trình chính thống, với một số ngoại lệ, chẳng hạn như các kênh kiểu trong Go. Một khó khăn là, bên cạnh các kiểu tin nhắn mà một kênh có thể truyền tải, bạn cũng cần phải suy nghĩ về giao thức cho việc truyền tin nhắn. Nói cách khác, bên cạnh việc quyết định nội dung gửi đi (kiểu), bạn cũng cần phải nghĩ về thời điểm gửi nó (giao thức).

Tuy nhiên, đã có nhiều nghiên cứu đáng kể về các loại cho lập trình đồng thời, nổi bật nhất là nghiên cứu về kiểu phiên (session types) bắt đầu với bài báo năm 1993 của Kohei Honda "Các kiểu cho Tương tác Đôi". Kiểu mà chúng ta sẽ triển khai trong phần này là một trường hợp của kiểu phiên với một giao thức tối thiểu, trong đó một khách hàng gửi một tin nhắn và sau đó nhận một phản hồi. Nếu bạn quan tâm đến việc khám phá thêm, một bài báo gần đây (năm 2016) mang tên "Chứng nhận Dữ liệu trong Các Kiểu Phiên Đa Bên" của Bernardo Toninho và Nobuko Yoshida, mô tả một cách sử dụng các loại trong các chương trình đồng thời phức tạp hơn.

Chúng tôi sẽ không thực hiện đúng việc triển khai này ngay lần đầu tiên. Như thường thấy trong phát triển dựa trên kiểu, chúng tôi sẽ nhận ra rằng cần phải tinh chỉnh kiểu để giải quyết các vấn đề xuất hiện sau nỗ lực đầu tiên của chúng tôi. Chúng tôi sẽ bắt đầu bằng việc định nghĩa một kiểu cụ thể cho dịch vụ cộng, và sau đó sẽ tinh chỉnh nó để hỗ trợ các dịch vụ tổng quát mà được đảm bảo sẽ phản hồi các yêu cầu không giới hạn.

15.2.1.
Describing message-passing processes in a type

Trước đó, tôi đã mô tả hai vấn đề với kiểu Channel nguyên thủy làm cho lập trình đồng thời, ở dạng nguyên thủy này, không an toàn:

There’s no way to check that a response to a request has the correct type.
There’s no way to check the correspondence between sending and receiving messages in communicating processes.

Chúng ta sẽ giải quyết cả hai vấn đề này bằng cách định nghĩa một kiểu để mô tả quy trình và sau đó tinh chỉnh nó khi cần thiết để hỗ trợ các tính năng truyền tin mà chúng ta cần.

Để bắt đầu, bạn có thể định nghĩa một loại quy trình hỗ trợ các hành động IO, xây dựng các giá trị thuần khiết và sắp xếp thứ tự.

Listing 15.6.
A type for describing processes (Process.idr)

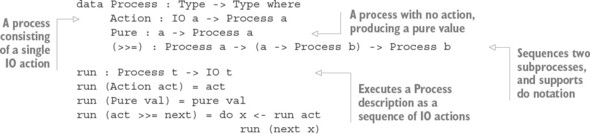
Using IO in Action

Bằng cách sử dụng IO trong hành động, bạn có thể bao gồm các hành động IO tùy ý trong các quá trình, chẳng hạn như ghi vào console hoặc đọc đầu vào của người dùng. Điều này hơi quá chung chung, vì các hành động IO bao gồm, bên cạnh những thứ khác, các nguyên thủy giao tiếp không an toàn. Bạn có thể hạn chế điều này bằng cách định nghĩa một loại lệnh chính xác hơn (xem chương 11 để biết ví dụ), nhưng chúng ta sẽ giữ lại IO cho ví dụ này.

Hiện tại, Process chỉ là một lớp bao bọc cho các chuỗi hành động IO. Bước tiếp theo là mở rộng nó để hỗ trợ việc tạo ra các tiến trình mới. Bạn có thể định nghĩa một kiểu dữ liệu để đại diện cho các tiến trình có thể nhận một Thông điệp, sử dụng PID từ System.Concurrency.Channels:

data MessagePID = MkMessage PID

Tiếp theo, bạn có thể thêm một hàm khởi tạo vào Process mô tả một hành động phát sinh một quá trình mới và trả về MessagePID của quá trình đó, nếu nó thành công.

Spawn : Process () -> Process (Maybe MessagePID)

Bạn cũng cần mở rộng run để có thể thực thi lệnh Spawn mới. Lệnh này tạo một tiến trình mới bằng cách sử dụng nguyên thủy spawn và sau đó trả về một MessagePID chứa PID mới.

run (Spawn proc) = do Just pid <- spawn (run proc) | Nothing => pure Nothing pure (Just (MkMessage pid))

Adding new constructors

Hãy nhớ rằng sau khi bạn thêm constructor Spawn, bạn có thể thêm các trường hợp còn thiếu để chạy trong Atom bằng cách nhấn Ctrl-Alt-A khi con trỏ ở trên tên run.

Tiếp theo, bạn có thể thêm lệnh để cho phép các tiến trình gửi tin nhắn cho nhau. Trong các ví dụ trước, tiến trình chính đã gửi yêu cầu loại Message và chờ đợi các phản hồi tương ứng loại Nat. Bạn có thể gói gọn hành vi này trong một lệnh Request duy nhất:

Request : MessagePID -> Message -> Process (Maybe Nat)

Lý do để trả về Maybe Nat, thay vì Nat, là vì bạn không có bất kỳ đảm bảo nào rằng quá trình mà MessagePID đề cập vẫn đang chạy. Khi bạn thực hiện một yêu cầu, bạn sẽ cần kết nối với quá trình xử lý yêu cầu, gửi cho nó một tin nhắn và sau đó chờ đợi phản hồi.

Encapsulating primitives in the Process type

Bạn vẫn cần sử dụng unsafeSend và unsafeRecv, nhưng bằng cách đóng gói chúng trong kiểu dữ liệu Process, bạn biết rằng chỉ có một nơi trong chương trình của bạn sử dụng các nguyên thủy không an toàn. Bạn cần cẩn thận để định nghĩa đúng, nhưng một khi bạn làm điều đó, bạn biết rằng bất kỳ chương trình truyền tin nào được thực hiện dựa trên kiểu Process sẽ tuân theo giao thức truyền tin một cách chính xác.

Quá trình cộng chờ một tin nhắn đến, tính toán kết quả và gửi lại phản hồi cho người yêu cầu. Bạn có thể đóng gói hành vi này trong một lệnh Respond đơn.

Respond : ((msg : Message) -> Process Nat) -> Process (Maybe Message)

Điều này nhận một hàm làm tham số, hàm này, khi được cung cấp một thông điệp nhận được từ một yêu cầu, sẽ tính toán giá trị Nat để gửi lại. Nó trả về một giá trị có kiểu Maybe Message, có thể là Nothing, nếu nó không xử lý được thông điệp đến, hoặc ở dạng Just msg, nếu nó đã xử lý một thông điệp đến (msg). Điều này hữu ích nếu bạn cần thực hiện bất kỳ xử lý nào thêm với thông điệp đến, ngay cả sau khi đã gửi phản hồi.

Khi bạn chạy lệnh Respond, bạn sẽ chờ một giây cho một tin nhắn và sau đó, nếu có tin nhắn, tính toán phản hồi và gửi lại.

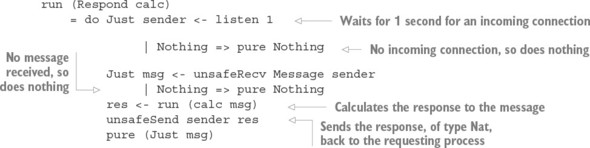
Alternative implementations for Respond

Việc cài đặt này của trường hợp Respond sẽ chờ trong 1 giây nếu không có tin nhắn đến. Một cài đặt thay thế, linh hoạt hơn, có thể cho phép người dùng chỉ định thời gian chờ. Ví dụ, nếu không có yêu cầu đến, có thể sẽ không hợp lý khi tiếp tục chờ đợi nếu một quy trình còn công việc khác phải làm.

Danh sách 15.7 cho thấy cách bạn có thể định nghĩa adder và main bằng cách sử dụng Process. Chúng tôi sẽ gọi chúng là procAdder và procMain để phân biệt với các phiên bản trước. Trong procAdder, bạn sử dụng Respond để giải thích cách phản hồi một Tin nhắn, và trong procMain, bạn sử dụng Request để gửi một tin nhắn đến một quá trình được khởi tạo.

Listing 15.7.
Implementing a type-safe adder process (Process.idr)

Bạn có thể thử điều này tại REPL, sử dụng run để chuyển procMain thành một chuỗi các hành động IO:

*Process> :exec run procMain 5

Khác với phiên bản trước, procMain không thể mong đợi nhận được một chuỗi thay vì một số tự nhiên, vì kiểu của Request không cho phép điều đó. Bạn cũng đã bao gói giao thức giao tiếp trên một kênh bằng cách sử dụng Request và Respond, vì vậy bạn biết rằng bạn sẽ không gửi hoặc nhận quá nhiều tin nhắn sau khi tạo một kênh.

Là một nỗ lực đầu tiên, điều này đã cải thiện hơn so với việc triển khai nguyên thủy với Channel, nhưng còn nhiều cách bạn có thể cải thiện nó. Ví dụ, procAdder không phải là tổng quát:

*Process> :total procAdder Main.procAdder is possibly not total due to recursive path: Main.procAdder

Điều này có thể trở thành vấn đề, vì một quy trình không tổng quát có thể không phản hồi thành công các yêu cầu. Là một sự tinh chỉnh đầu tiên, bạn có thể sửa đổi loại Quy trình, và tương ứng là định nghĩa về việc thực hiện, để các quy trình chạy vô hạn như proc-Adder trở thành tổng quát.

15.2.2.
Making processes total using Inf

Như bạn đã thấy trong chương 11, bạn có thể đánh dấu các phần dữ liệu là có thể vô hạn bằng cách sử dụng Inf:

Inf : Type -> Type

Bạn có thể nói rằng một hàm là tổng quát nếu nó tạo ra một tiền tố hữu hạn của các trình dựng dữ liệu của một kết quả vô hạn có kiểu đúng trong thời gian hữu hạn. Trong thực tế, điều này có nghĩa là bất cứ khi nào bạn sử dụng một giá trị có kiểu Inf, nó cần phải là một tham số của một trình dựng dữ liệu hoặc một chuỗi lồng nhau của các trình dựng dữ liệu.

Bạn đã thấy nhiều cách sử dụng Inf để định nghĩa các quá trình có thể vô hạn trong các chương 11 và 12. Ở đây, bạn có thể sử dụng nó để đánh dấu rõ ràng các phần của một quá trình lặp lại bằng cách thêm trình xây dựng sau vào Process:

Loop : Inf (Process a) -> Process a

Để tham khảo, danh sách tiếp theo cho thấy định nghĩa hiện tại của Quy trình, bao gồm Vòng lặp, được định nghĩa trong tệp mới, ProcessLoop.idr.

Listing 15.8.
New `Process` type, extended with `Loop` (ProcessLoop.idr)

Sử dụng Loop, bạn có thể định nghĩa procAdder như sau, ghi chú rõ ràng rằng lời gọi đệ quy đến procAdder là một quá trình có khả năng vô hạn:

procAdder : Process () procAdder = do Respond (\msg => case msg of Add x y => Pure (x + y)) Loop procAdder

Phiên bản này của procAdder là tổng:

*ProcessLoop> :total procAdder Main.procAdder is Total

Bằng cách sử dụng một bộ khởi tạo vòng lặp rõ ràng, bạn có thể đánh dấu các phần vô hạn của một Quy trình để ít nhất bạn có thể chắc chắn rằng bất kỳ đệ quy vô hạn nào đều được dự định. Hơn nữa, như bạn sẽ thấy trong phần tiếp theo, điều này sẽ cho phép bạn tinh chỉnh Quy trình hơn nữa để bạn có thể kiểm soát chính xác khi nào một quy trình được phép lặp lại.

Bạn cũng cần mở rộng hàm run để hỗ trợ Loop. Cách đơn giản nhất là thực hiện hành động trực tiếp:

run (Loop act) = run act

Thật không may, định nghĩa mới về chạy này không hoàn toàn vì bộ kiểm tra tính toàn vẹn (đúng!) không tin rằng hành động là một chuỗi nhỏ hơn Loop hành động.

*ProcessLoop> :total run Main.run is possibly not total due to recursive path: Main.run, Main.run, Main.run

Giống như các quá trình vô hạn trong chương 11, bạn có thể định nghĩa một kiểu dữ liệu Fuel để đưa ra một giới hạn rõ ràng cho việc thực thi. Mỗi lần bạn lặp, bạn sẽ giảm số lượng Fuel có sẵn. Danh sách sau đây cho thấy cách bạn có thể mở rộng hàm run để nó kết thúc khi hết Fuel, theo mẫu mà bạn đã thấy trong chương 11.

Listing 15.9.
New `run` function, with an execution limit (ProcessLoop.idr)

Hãy nhớ rằng bạn có thể tạo ra một lượng nhiên liệu vô hạn và cho phép các quá trình chạy vô thời hạn bằng cách sử dụng một hàm một phần duy nhất, mãi mãi:

partial forever : Fuel forever = More forever

Sử dụng một hàm vĩnh viễn duy nhất để xác định thời gian cho một quá trình không xác định cho phép chạy có nghĩa là bạn giảm thiểu số lượng hàm không tổng quát mà bạn cần. Bởi vì hàm chạy là tổng quát, bạn biết rằng nó sẽ tiếp tục thực hiện các hành động của quá trình miễn là còn hành động để thực hiện. Để tiện lợi, bạn cũng có thể định nghĩa một hàm để khởi tạo một quá trình và loại bỏ kết quả của nó:

partial runProc : Process () -> IO () runProc proc = do run forever proc pure ()

Sau đó, bạn có thể thử thực hiện procMain như sau, điều này sẽ hiển thị kết quả là 5 như trước.

*ProcessLoop> :exec runProc procMain 5

Sử dụng Loop, bạn có thể viết các quy trình lặp mãi mãi và là tổng quát bằng cách rõ ràng về thời điểm chúng lặp. Thật không may, tuy nhiên, vẫn không có đảm bảo rằng một quy trình lặp sẽ phản hồi bất kỳ tin nhắn nào. Ví dụ, bạn có thể định nghĩa procAdder như sau:

procAdderBad1 : Process () procAdderBad1 = do Action (putStrLn "I'm out of the office today") Loop procAdderBad1

Hoặc thậm chí như thế này:

procAdderBad2 : Process () procAdderBad2 = Loop procAdderBad2

Cả hai chương trình này đều được kiểm tra kiểu và đều được xác minh là tổng quát, nhưng không chương trình nào sẽ phản hồi lại bất kỳ thông điệp nào vì không có lệnh Respond. Trong trường hợp của proc-AdderBad2, nó được coi là tổng quát vì lời gọi đệ quy đến proc-AdderBad2 là một tham số của bộ tạo Loop, vì vậy nó sẽ tạo ra một tiền tố hữu hạn của các bộ tạo. Do đó, việc tổng quát khi sử dụng Loop không đủ để đảm bảo rằng một tiến trình sẽ phản hồi lại yêu cầu.

The meaning of totality, in practice

Toàn vẹn có nghĩa là bạn được đảm bảo rằng một hàm hoạt động đúng như cách được mô tả bởi kiểu của nó, vì vậy nếu kiểu không đủ chính xác, thì lời hứa đó cũng không chính xác! Với Process, kiểu không đủ chính xác để đảm bảo rằng một quy trình chứa lệnh Respond trước bất kỳ vòng lặp nào.

Hơn nữa, loại Quy trình rất cụ thể cho vấn đề viết một dịch vụ đồng thời để thêm số. Thế còn nếu bạn muốn viết các dịch vụ khác? Bạn không muốn phải viết một loại Quy trình khác cho mọi loại dịch vụ mà bạn có thể muốn tạo ra.

Để giải quyết những vấn đề này, bạn sẽ cần tinh chỉnh loại Quy trình theo hai cách nữa:

In section 15.2.3, you’ll refine it to ensure that a server process responds to requests on every iteration of a Loop.
In section 15.2.4, you’ll see how to use first-class types to allow Process to respond to any kind of message.

15.2.3.
Guaranteeing responses using a state machine and Inf

Trong chương 13, bạn đã thấy cách đảm bảo rằng các hệ thống sẽ thực hiện các hành động cần thiết theo đúng thứ tự bằng cách biểu diễn một máy trạng thái trong một kiểu. Một quy trình máy chủ như adder có thể ở một trong nhiều trạng thái, tùy thuộc vào việc nó đã nhận và xử lý yêu cầu hay chưa:

NoRequest—It has not yet serviced any requests.
Sent—It has sent a response to a request.
Complete—It has completed an iteration of a loop and is ready to service the next request.

Hình 15.3 minh họa cách mà các lệnh Respond và Loop ảnh hưởng đến trạng thái của một quy trình.

Figure 15.3.
A state transition diagram showing the states and operations in a server process. A process begins in the `NoRequest` state and must end in the `Complete` state, meaning that it has responded to at least one request.

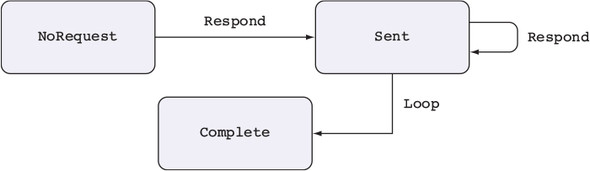
Nếu bạn có một quy trình bắt đầu ở trạng thái NoRequest và kết thúc ở trạng thái Complete, bạn có thể chắc chắn rằng nó đã phản hồi một yêu cầu, vì cách duy nhất để đạt được trạng thái Complete là gọi Respond. Bạn cũng có thể chắc chắn rằng nó đang tiếp tục nhận yêu cầu, vì cách duy nhất để đạt được trạng thái Complete là gọi Loop. Bằng cách thể hiện trạng thái của một quy trình trong loại của nó, bạn có thể đưa ra những đảm bảo mạnh mẽ hơn về cách mà quy trình đó hoạt động.

Bạn có thể tinh chỉnh loại Quy trình để biểu thị các trạng thái trước và sau khi quy trình được thực thi:

Các trạng thái trong loại cho biết các điều kiện tiên quyết và hậu quả của một quy trình. Ví dụ:

Process () NoRequest Complete is the type of a process that responds to a request and then loops.
Process () NoRequest Sent is the type of a process that responds to one or more requests and then terminates.
Process () NoRequest NoRequest is the type of a process that responds to no requests and then terminates.

Danh sách 15.10 hiển thị Quy trình tinh chỉnh, nơi loại của mỗi lệnh giải thích cách nó ảnh hưởng đến trạng thái tổng thể của quy trình. Trong định nghĩa này, khi không có điều kiện tiên quyết nào về trạng thái và không có thay đổi trong trạng thái, cả trạng thái đầu vào và đầu ra đều là st.

Listing 15.10.
Annotating the `Process` type with its input and output states (ProcessState.idr)

Return type of Request

Trước đây, bạn đã gửi các yêu cầu loại Message và nhận các phản hồi loại Maybe Nat. Bạn đã sử dụng Maybe vì bạn không có đảm bảo rằng dịch vụ vẫn đang hoạt động, vì vậy yêu cầu có thể bị thất bại. Bây giờ, bạn đã thiết lập trạng thái Process để các dịch vụ sẽ luôn phản hồi các yêu cầu. Nếu bạn gửi một yêu cầu, bạn được đảm bảo nhận được phản hồi loại Nat trong một khoảng thời gian hữu hạn.

Khi bạn sử dụng định nghĩa mới này, không có cách nào để một hàm có thể gọi Loop trừ khi hàm đó có thể thỏa mãn điều kiện tiên quyết là nó đã gửi một phản hồi cho một yêu cầu. Hơn nữa, Loop cũng là cách duy nhất để một quá trình đạt đến trạng thái Hoàn thành. Do đó, bạn chỉ có thể gọi Loop trên một quá trình mà được đảm bảo là đang lặp lại, vì quá trình đó phải bắt đầu ở trạng thái NoRequest và kết thúc ở trạng thái Hoàn thành.

Bạn vẫn có thể định nghĩa procAdder như trước, vì mỗi lệnh đều thỏa mãn điều kiện tiên quyết, và loại của nó bây giờ chỉ ra rằng nó phải phản hồi một yêu cầu và sau đó lặp lại:

procAdder : Process () NoRequest Complete procAdder = do Respond (\msg => case msg of Add x y => Pure (x + y)) Loop procAdder

Hai phiên bản không đúng đã được định nghĩa trước đó, tuy nhiên, chúng không còn được kiểm tra kiểu vì các lệnh không đáp ứng các điều kiện tiên quyết do Process đưa ra khi bạn cố gắng sử dụng chúng. Ví dụ, bạn có thể thử định nghĩa sau:

procAdderBad1 : Process () NoRequest Complete procAdderBad1 = do Action (putStrLn "I'm out of the office today") Loop procAdder

Idris báo cáo một lỗi vì không có Respond trước vòng lặp:

ProcessState.idr:63:21: When checking right hand side of procAdderBad1 with expected type Process () NoRequest Complete When checking an application of constructor Main.>>=: Type mismatch between Process a Sent Complete (Type of Loop _) and Process () NoRequest Complete (Expected type) Specifically: Type mismatch between Sent and NoRequest

Thông báo lỗi này có nghĩa là khi bạn gọi Loop, quá trình dự kiến phải ở trạng thái Đã Gửi, nhưng tại thời điểm này nó đang ở trạng thái Không Yêu Cầu, chưa gửi bất kỳ phản hồi nào. Bạn sẽ nhận được một thông báo lỗi tương tự vì lý do tương tự với định nghĩa sau:

procAdderBad2 : Process () NoRequest Complete procAdderBad2 = Loop procAdderBad2

Để thực thi các chương trình sử dụng Quy trình tinh chỉnh, bạn sẽ cần sửa đổi run và runProc. Trước tiên, bạn cần thay đổi kiểu của chúng:

run : Fuel -> Process t in_state out_state -> IO (Maybe t) runProc : Process () in_state out_state -> IO ()

Các định nghĩa chủ yếu vẫn giữ nguyên như các phiên bản trước. Thay đổi duy nhất là trong định nghĩa của trường hợp Yêu cầu trong quá trình chạy, bây giờ mà bạn biết rằng một Yêu cầu sẽ luôn nhận được phản hồi trong thời gian hữu hạn:

Return value of run

Nếu quá trình không thành công vì lý do nào đó, nó sẽ trả về Nothing. Cho đến bây giờ, điều này chỉ có thể xảy ra nếu nó hết nhiên liệu. Bạn đã thiết lập Quy trình để người gửi và người nhận được phối hợp, vì vậy, ít nhất là về lý thuyết, việc giao tiếp không thể thất bại. Nếu việc giao tiếp thất bại, thì có thể có lỗi trong việc triển khai quá trình hoặc một lỗi nghiêm trọng hơn trong thời gian chạy, vì vậy bạn cũng có thể trả về Nothing trong trường hợp này.

Bạn cũng sẽ cần sửa đổi kiểu của procMain để phù hợp với kiểu Process đã được tinh chỉnh. Kiểu này rõ ràng chỉ ra rằng procMain không có ý định phản hồi bất kỳ yêu cầu nào đến vì nó kết thúc ở trạng thái NoRequest.

procMain : Process () NoRequest NoRequest

Thật tiện lợi khi định nghĩa các từ đồng nghĩa cho kiểu cho các client, như procMain, và cho các dịch vụ, như procAdder. Chúng đều sử dụng Process, nhưng chúng khác nhau về cách chúng ảnh hưởng đến trạng thái của quá trình:

Service : Type -> Type Service a = Process a NoRequest Complete Client : Type -> Type Client a = Process a NoRequest NoRequest

Danh sách dưới đây cho thấy các định nghĩa được tinh chỉnh của procAdder và procMain sử dụng các từ đồng nghĩa kiểu này cho các quy trình máy khách và máy chủ.

Listing 15.11.
Refined definitions of `procAdder` and `procMain` (ProcessState.idr)

Nếu bạn thử điều này tại REPL, bạn sẽ thấy nó hiển thị 5 như trước.

*ProcessState> :exec runProc procMain 5

Bạn bây giờ có một định nghĩa về Quy trình với những đảm bảo sau đây, được đảm bảo bởi các điều kiện tiên quyết và điều kiện hậu quả trong định nghĩa của Quy trình:

All requests of type Message are sent responses of type Nat.
Every process started with Spawn is guaranteed to loop indefinitely and respond to requests on every iteration.
Therefore, every time a process sends a Request to a service started with Spawn, it will receive a response in finite time as long as the service is defined by a total function.

Điều này có nghĩa là bạn có thể viết các chương trình đồng thời an toàn về kiểu dữ liệu mà không bị deadlock, vì mỗi yêu cầu đều được đảm bảo sẽ nhận được phản hồi vào một thời điểm nào đó. Nhưng ở giai đoạn này, nó chỉ cho phép bạn viết một loại dịch vụ—một loại dịch vụ nhận một Thông điệp và gửi lại một số tự nhiên. Nó sẽ hữu ích hơn rất nhiều nếu bạn có thể định nghĩa các quy trình truyền thông điệp tổng quát với các tương tác do người dùng định nghĩa giữa người gửi và người nhận. Như bạn sẽ thấy, bạn có thể đạt được điều này với một sự tinh chỉnh cuối cùng cho Process.

15.2.4.
Generic message-passing processes

Khi một quy trình nhận được một yêu cầu có dạng Add x y, nó sẽ gửi lại một phản hồi thuộc loại Nat. Bạn có thể biểu diễn mối quan hệ này giữa các loại yêu cầu và phản hồi trong một hàm cấp độ loại:

AdderType : Message -> Type AdderType (Add x y) = Nat

Chức năng này mô tả giao diện mà Process hỗ trợ: nếu nó nhận được một tin nhắn có dạng Add x y, nó sẽ gửi phản hồi có kiểu Nat. Bạn có thể định nghĩa các giao diện khác theo cách này; ví dụ, danh sách sau đây cung cấp một mô tả về giao diện cho một quy trình đáp ứng các yêu cầu thực hiện các thao tác trên danh sách.

Listing 15.12.
Describing an interface for `List` operations

Nói chung, một giao diện cho một quy trình là một hàm như AdderType hoặc ListType, tính toán một loại phản hồi từ một yêu cầu. Thay vì xác định một loại cụ thể mà các quy trình có thể gửi và nhận, bạn có thể bao gồm giao diện như một phần của loại quy trình bằng cách thêm một tham số bổ sung cho giao diện, như hình 15.4 cho thấy.

Figure 15.4.
A refined `Process` type, including the interface that the process responds to as part of the type

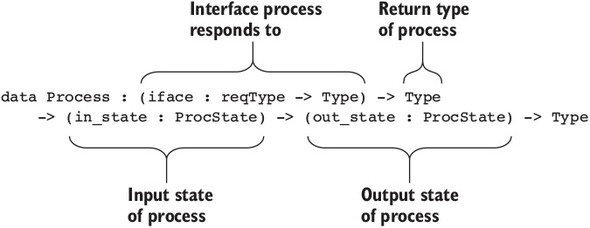
Request type of Process

Tham số iface trong Process bao gồm một biến kiểu, reqType. Đây là một tham số ngầm định, và nó xác định loại tin nhắn mà tiến trình có thể nhận. Idris sẽ suy diễn reqType từ tham số iface. Ví dụ, trong procAdder, iface là AdderType, vì vậy reqType phải là Message.

Chúng ta sẽ đến với định nghĩa tinh tế của Quy trình sớm thôi. Khi nó được định nghĩa, dịch vụ procAdder sẽ phản hồi với một giao diện được định nghĩa bởi AdderType:

procAdder : Process AdderType () NoRequest Complete

Một số quá trình, như procMain, không phản hồi bất kỳ yêu cầu nào. Bạn có thể làm điều này rõ ràng trong kiểu bằng cách định nghĩa các giao diện của chúng như sau:

NoRecv : Void -> Type NoRecv = const Void

Nhớ từ chương 8 rằng Void là kiểu rỗng, không có giá trị. Bởi vì bạn không bao giờ có thể tạo ra một giá trị của kiểu Void, một quá trình cung cấp giao diện NoRecv sẽ không bao giờ nhận được yêu cầu. Bạn có thể sử dụng nó trong kiểu sau cho procMain:

procMain : Process NoRecv () NoRequest NoRequest

Bạn cũng cần định nghĩa lại các từ đồng nghĩa kiểu Service và Client để bao gồm mô tả giao diện. Một Service có một giao diện, nhưng một Client không nhận bất kỳ yêu cầu nào:

Service : (iface : reqType -> Type) -> Type -> Type Service iface a = Process iface a NoRequest Complete Client : Type -> Type Client a = Process NoRecv a NoRequest NoRequest

Khi bạn tạo một tiến trình mới, bạn nhận được một PID cho tiến trình mới đó dưới dạng MessagePID. Bạn chỉ nên gửi tin nhắn đến một tiến trình khi các tin nhắn phù hợp với giao diện của tiến trình đó, vì vậy bạn có thể làm rõ MessagePID để bao gồm giao diện mà nó hỗ trợ trong kiểu của nó:

data MessagePID : (iface : reqType -> Type) -> Type where MkMessage : PID -> MessagePID iface

Bây giờ, nếu bạn có một PID kiểu MessagePID AdderType, bạn biết rằng bạn có thể gửi các tin nhắn kiểu Message cho nó, vì đó là kiểu đầu vào của AdderType.

Tổng hợp tất cả những điều này, bạn có thể tinh chỉnh Process để mô tả giao diện của chính nó và rõ ràng về thời điểm an toàn để gửi một yêu cầu của một loại cụ thể đến một Process khác. Danh sách tiếp theo hiển thị các loại đã được tinh chỉnh cho Request, Respond và Spawn.

Listing 15.13.
Refining `Process` to include its interface in the type, part 1 (ProcessIFace.idr)

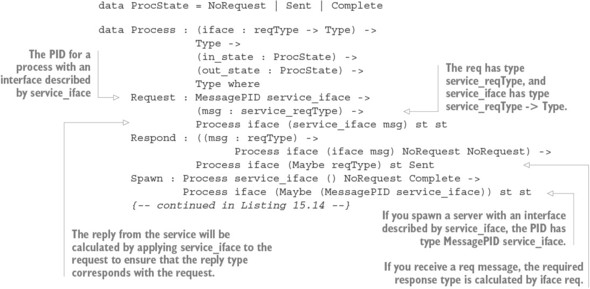
Danh sách sau đây hoàn thành định nghĩa tinh chỉnh của Process, thêm Loop, Action, Pure và (>>=). Trong mỗi trường hợp, tất cả những gì bạn cần làm là thêm một tham số iface cho Process.

Listing 15.14.
Refining `Process` to include its interface in the type, part 2 (ProcessIFace.idr)

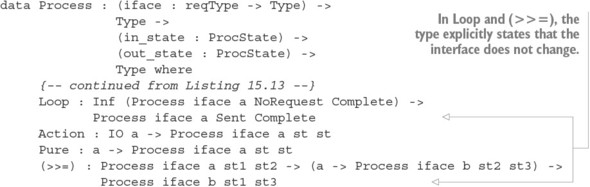
Cuối cùng, bạn cần cập nhật run và runProc cho định nghĩa quy trình đã được tinh chỉnh. Danh sách 15.15 cho thấy những thay đổi bạn cần thực hiện đối với run. Bạn chỉ cần sửa đổi các trường hợp cho Request và Respond để làm rõ về các loại tin nhắn mà một quy trình mong đợi nhận được.

Listing 15.15.
Updating `run` for the refined `Process` (ProcessIFace.idr)

Đối với runProc, bạn chỉ cần thay đổi kiểu của nó để thêm tham số iface vào Process:

partial runProc : Process iface () in_state out_state -> IO () runProc proc = do run forever proc pure ()

Khi thiết kế các kiểu dữ liệu, đặc biệt là những kiểu cung cấp các đảm bảo mạnh mẽ như Process, thường thì một ý tưởng tốt là bắt đầu bằng cách cố gắng giải quyết một vấn đề cụ thể trước khi chuyển sang giải pháp tổng quát hơn. Ở đây, chúng tôi bắt đầu với một kiểu cho Process chỉ hỗ trợ các kiểu thông điệp và phản hồi cụ thể (Message và Nat). Chỉ sau khi điều đó hoạt động, chúng tôi mới sử dụng các hàm cấp kiểu để tạo ra một kiểu Process tổng quát.

15.2.5.
Defining a module for Process

Khi bạn đã định nghĩa một kiểu tổng quát, điều hữu ích là tạo một mô-đun mới để làm cho kiểu đó và các hàm hỗ trợ của nó có sẵn cho những người dùng khác. Chúng tôi sẽ định nghĩa một mô-đun mới, ProcessLib.idr, định nghĩa Process và các định nghĩa hỗ trợ và xuất khẩu chúng khi cần thiết.

Danh sách tiếp theo cho thấy cấu trúc tổng thể của mô-đun, bỏ qua các định nghĩa nhưng thêm các sửa đổi xuất khẩu vào mỗi khai báo.

Listing 15.16.
Defining `Process` in a module, omitting definitions (ProcessLib.idr)

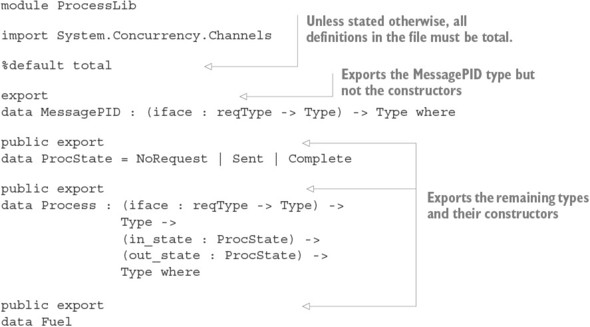
Các định nghĩa hoàn chỉnh giống như những định nghĩa bạn đã thấy cho MessagePID, ProcState, Process và Fuel. Hãy nhớ từ chương 10 rằng đối với các khai báo dữ liệu, một bộ sửa đổi xuất có thể là một trong những điều sau đây:

export—The type constructor is exported but not the data constructors.
public export—The type and data constructors are exported.

Danh sách sau đây cho thấy cách bạn có thể xuất khẩu các chức năng hỗ trợ.

Listing 15.17.
Supporting function types for `Process`, omitting definitions (ProcessLib.idr)

Đối với các hàm, một bộ sửa đổi xuất có thể là một trong những điều sau đây:

export—The type is exported but not the definition.
public export—The type and definition are exported.

Trừ khi có lý do cụ thể để xuất định nghĩa cũng như kiểu, tốt hơn là chỉ sử dụng xuất, ẩn chi tiết của định nghĩa. Ở đây, bạn sử dụng xuất công khai cho Client và Service vì đây là các từ đồng nghĩa kiểu, và các mô-đun khác sẽ cần biết rằng chúng được định nghĩa dựa trên Process.

Bây giờ, khi bạn đã định nghĩa Process và một mô-đun ProcessLib riêng biệt xuất khẩu các định nghĩa liên quan, chúng ta có thể thử nghiệm thêm nhiều ví dụ. Để kết thúc phần này, chúng ta sẽ xem hai ví dụ về việc triển khai các chương trình đồng thời sử dụng loại Process tổng quát này. Đầu tiên, chúng ta sẽ triển khai một quy trình sử dụng ListType, đã được định nghĩa trước đó trong danh sách 15.12, và sau đó chúng ta sẽ xem một ví dụ lớn hơn sử dụng đồng thời để chạy một quy trình ở chế độ nền để đếm số từ trong một tệp.

15.2.6.
Example 1: List processing

Để chứng minh cách bạn có thể sử dụng Process để định nghĩa các dịch vụ khác ngoài procAdder, chúng ta sẽ bắt đầu với một dịch vụ phản hồi các yêu cầu thực hiện các chức năng trên List. Giao diện của dịch vụ được định nghĩa bởi một hàm ListType. Nó cung cấp hai hoạt động: Length và Append.

data ListAction : Type where Length : List elem -> ListAction Append : List elem -> List elem -> ListAction ListType : ListAction -> Type ListType (Length xs) = Nat ListType (Append {elem} xs ys) = List elem

Chúng tôi sẽ định nghĩa một dịch vụ procList phản hồi các yêu cầu trên giao diện này. Nó có kiểu sau:

procList : Service ListType ()

Bạn có thể định nghĩa procList một cách từng bước, thực hiện các bước sau:

Define, type—As with procAdder, you can implement procList as a loop that responds to a request on each iteration:
```
procList : Service ListType () procList = do Respond (\msg => ?procList_rhs) Loop procList
```
Looking at the ?procList_rhs type here, you can see that the type you need to produce is calculated from the msg you receive:
```
 msg : ListAction -------------------------------------- procList_rhs : Process ListType (ListType msg) NoRequest NoRequest
```

Define— Because the type you need to produce depends on the value of msg, you can continue the definition with a case statement, inspecting msg:

procList : Service ListType () procList = do Respond (\msg => case msg of case_val => ?procList_rhs) Loop procList

Case splitting on case_val produces this:

procList : Service ListType () procList = do Respond (\msg => case msg of Length xs => ?procList_rhs_1 Append xs ys => ?procList_rhs_2) Loop procList

Type, refine—For ?procList_rhs_1, if you check the type, you’ll see that you need to produce a Nat for the result of Length xs:

 msg : ListAction a : Type xs : List elem -------------------------------------- procList_rhs_1 : Process ListType Nat NoRequest NoRequest

You can refine ?procList_rhs_1 as follows:

procList : Service ListType () procList = do Respond (\msg => case msg of Length xs => Pure (length xs) Append xs ys => ?procList_rhs_2) Loop procList

Refine— To refine ?procList_rhs_2, you need to provide a List elem, and you can complete the definition as follows:

procList : Service ListType () procList = do Respond (\msg => case msg of Length xs => Pure (length xs) Append xs ys => Pure (xs ++ ys)) Loop procList

Sau khi hoàn thành procList, bạn có thể thử nghiệm nó bằng cách khởi động nó trong một tiến trình và gửi các yêu cầu tới nó. Danh sách dưới đây định nghĩa một tiến trình gửi hai yêu cầu đến một instance của procList và hiển thị kết quả của chúng.

Listing 15.18.
A main program that uses the `procList` service (ListProc.idr)

Bạn có thể thử điều này tại REPL như sau:

*ListProc> :exec runProc procMain 3 [1, 2, 3, 4, 5, 6]

Giống như procAdder, procList lặp lại, chờ đợi các yêu cầu đến và xử lý chúng khi cần thiết, nhưng nó không thực hiện bất kỳ phép toán nào khác trong khi chờ đợi yêu cầu. Các tiến trình đồng thời trở nên hữu ích hơn nhiều nếu, thay vì dành thời gian chờ đợi và giữ yên lặng cho các yêu cầu từ các tiến trình khác, chúng cũng thực hiện một số phép toán. Trong ví dụ tiếp theo, bạn sẽ thấy cách làm điều này.

15.2.7.
Example 2: A word-counting process

Khi bạn định nghĩa các dịch vụ, bạn có thể xác định các yêu cầu riêng biệt để khởi động một hành động và nhận kết quả của hành động đó. Ví dụ, nếu bạn đang định nghĩa một dịch vụ đếm từ, bạn có thể cho phép một khách hàng thực hiện các bước sau:

Send a request to a word-count service to load a file and count the number of words in the file.
While the word-count service is processing, the client continues its own work, such as reading input and producing output.
Send a second request to the word-count service to ask how many words were in the file.

Trong ví dụ này, bạn sẽ định nghĩa dịch vụ đếm từ dựa trên bản ghi WCData và hàm doCount được định nghĩa trong danh sách 15.19. Hàm này nhận nội dung của một tệp, dưới dạng chuỗi, và tạo ra một cấu trúc chứa số lượng từ và số dòng trong nội dung đó.

Listing 15.19.
A small function to count the number of words and lines in a `String` (WordCount.idr)

Bạn có thể xem một ví dụ về điều này đang hoạt động tại REPL:

*WordCount> doCount "test test\ntest" MkWCData 2 3 : WCData

Mục tiêu là triển khai một quy trình cung cấp dịch vụ đếm từ. Thay vì tải và đếm số từ trong một yêu cầu duy nhất, bạn có thể cung cấp hai lệnh:

CountFile—Given a filename, loads that file and counts the number of words in it
GetData—Given a filename, returns the WCData structure for that file, as long as the file has already been processed with CountFile

Thay vì trả về chính cấu trúc WCData, CountFile sẽ trả về ngay lập tức và tiếp tục tải tệp trong một quy trình riêng biệt. Điều này có nghĩa là một yêu cầu bắt đầu nhiệm vụ và một yêu cầu khác sẽ truy xuất kết quả. Điều này sẽ cho phép người yêu cầu tiếp tục công việc của họ trong khi dịch vụ đếm từ đang xử lý tệp. Đoạn mã dưới đây cho thấy giao diện và một định nghĩa sơ bộ cho dịch vụ đếm từ.

Listing 15.20.
Interface for the word-count service (WordCount.idr)

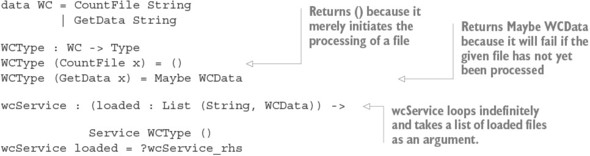
Chúng ta sẽ đến định nghĩa của wcService trong giây lát. Danh sách tiếp theo cho thấy cách bạn có thể gọi nó và tiếp tục thực hiện các hành động tương tác ở chế độ nền trong khi wcService đang xử lý một tệp trong nền.

Listing 15.21.
Using the word-count service (WordCount.idr)

Danh sách 15.22 trình bày một triển khai chưa hoàn chỉnh của wcService cho thấy cách nó phản hồi các lệnh CountFile và GetData. Hai phần của định nghĩa còn thiếu:

Loading and processing the requested file
Looping, with the new file information added to the input, loaded

Listing 15.22.
Responding to commands in `wcService` (WordCount.idr)

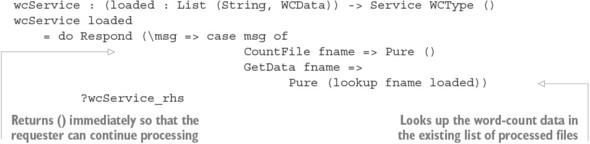
Để xử lý đầu vào, bạn có thể xem giá trị trả về từ Respond. Hãy nhớ rằng Respond có kiểu sau:

Respond : ((msg : reqType) -> Process iface (iface msg) NoRequest NoRequest) -> Process iface (Maybe reqType) st Sent

Giá trị trả về từ Respond, loại Maybe reqType, cho bạn biết tin nhắn nào, nếu có, đã được nhận. Nếu wcService nhận lệnh CountFile, nó có thể tải và xử lý tệp cần thiết trước khi xử lý đầu vào tiếp theo của nó.

Danh sách tiếp theo cho thấy một sự tinh chỉnh thêm của wcService, vẫn bao gồm một lỗ trống cho chức năng xử lý tệp.

Listing 15.23.
Incomplete implementation of `wcService` (WordCount.idr)

Để xem bạn cần làm gì để hoàn thành wcService, bạn có thể kiểm tra loại của ?countFile:

 loaded : List (String, WCData) fname : String msg2 : Maybe WC st2 : ProcState a : Type -------------------------------------- countFile : List (String, WCData) -> String -> Process WCType (List (String, WCData)) Sent Sent

`countFile cần phải là một hàm nhận vào danh sách hiện tại của dữ liệu tệp đã xử lý và một tên tệp, rồi trả về một danh sách cập nhật về dữ liệu tệp đã xử lý. Danh sách tiếp theo cho thấy cách định nghĩa nó bằng cách sử dụng doCount, được định nghĩa trước đó, để xử lý nội dung của tệp.`

Listing 15.24.
Loading a file and counting words (WordCount.idr)

Updating the hole for countFile

Hãy nhớ rằng bạn cần định nghĩa countFile trước khi sử dụng nó trong wcService. Sau khi bạn đã định nghĩa countFile, đừng quên thay thế lỗ ?countFile bằng một lời gọi đến countFile.

Bây giờ bạn đã định nghĩa countFile, bạn có thể thử thực thi procMain, điều này sẽ khởi động wcService, yêu cầu đếm số từ trong một tệp, test.txt, và sau đó hiển thị kết quả. Bạn sẽ cần tạo một tệp test.txt với nội dung giống như sau:

test test test test test test test

Bạn có thể thực thi procMain tại REPL như sau:

Với Process, bạn đã định nghĩa một loại cho phép bạn mô tả các quy trình thực thi đồng thời và giải thích cách các quy trình có thể gửi tin nhắn cho nhau một cách an toàn, theo một giao thức:

A service must respond to every message it receives, on a specific interface, and continue responding in a loop.
A client can then send a message to a process, with the correct interface, and be sure of receiving a reply of the correct type.

Điều này không giải quyết tất cả các vấn đề lập trình song song có thể, nhưng bạn đã định nghĩa một kiểu dữ liệu bao gói hành vi của một loại chương trình đồng thời. Nếu một hàm mô tả một loại Process được kiểm tra kiểu và là tổng quát, bạn có thể yên tâm rằng nó sẽ không gặp phải tình trạng deadlock và rằng tất cả các yêu cầu sẽ nhận được phản hồi. Nếu bạn sau này tinh chỉnh Process thêm, chẳng hạn bằng cách cho phép những mô tả phức tạp hơn về các tương tác giữa các tiến trình, bạn sẽ có thể triển khai các mô hình phức tạp hơn của các chương trình đồng thời.

15.3. Summary

Concurrent programming involves multiple processes executing simultaneously.
Processes in Idris cooperate with each other by sending messages.
The System.Concurrency.Channels library provides primitive, but unsafe, operations for message passing.
Primitive operations are unsafe because they provide no guarantees about when processes send and receive messages, or about the correspondence between the types of sent and received messages.
You can define a type for describing safe message-passing processes, implemented using Channel as a primitive.
Using Inf, you can guarantee that looping processes continue to perform IO actions.
By defining a state machine in the type, you can be sure that a process will respond to messages on every iteration of a loop.
The type of a process can be generic and describe the types of messages to which a process will respond.

Appendix A.
Installing Idris and editor modes

Phụ lục này giải thích cách cài đặt Idris. Có các bản phân phối nhị phân đã được xây dựng sẵn cho Mac và Windows, hoặc bạn có thể cài đặt từ mã nguồn trên bất kỳ hệ điều hành theo kiểu Unix nào. Nó cũng mô tả cách cài đặt chế độ Idris trong trình soạn thảo văn bản Atom.

The Idris compiler and environment

Tại thời điểm viết, Idris có sẵn dưới dạng phân phối nhị phân cho Windows và Mac OS từ http://idris-lang.org/download. Điều này bao gồm trình biên dịch và REPL, cùng với Prelude, thư viện cơ bản và nhiều thư viện được đóng góp hỗ trợ các cấu trúc dữ liệu khác nhau, mạng lưới và lập trình với tác dụng phụ.

Trong các phần tiếp theo, tôi sẽ mô tả cách cài đặt Idris, có thể là dưới dạng tệp nhị phân hoặc từ mã nguồn. Trong cả hai trường hợp, để kiểm tra rằng Idris đã được cài đặt thành công, bạn có thể chạy lệnh idris --version, lệnh này sẽ báo cáo phiên bản Idris đang được cài đặt:

$ idris --version 1.0

Mac OS

Phiên bản mới nhất của Idris luôn có sẵn dưới dạng gói nhị phân, có thể tải xuống tại http://idris-lang.org/pkgs/idris-current.pkg. Để có thể biên dịch và chạy các chương trình của bạn, bạn cũng cần cài đặt Xcode, có sẵn từ App Store.

Để cài đặt Idris, bạn có thể làm theo các bước sau:

Download idris-current.pkg.
Ensure that Xcode is installed from the App Store.
Open idris-current.pkg and follow the instructions. This will install the Idris binary to /usr/local/bin/idris.

Bạn cũng có thể cài đặt phiên bản mới nhất qua Homebrew (http://brew.sh/):

$ brew install idris

Windows

Các tệp nhị phân đã được xây dựng sẵn của Idris có sẵn tại https://github.com/idris-lang/Idris-dev/wiki/Windows-Binaries. Các tệp nhị phân này bao gồm tất cả những gì cần thiết để biên dịch và chạy các chương trình Idris.

Unix-like platforms, installing from source

Idris được triển khai bằng Haskell, và một bản phân phối nguồn có sẵn từ trình quản lý gói Haskell, Hackage (http://hackage.haskell.org/). Đây là một lựa chọn tốt nếu bạn đang sử dụng hệ điều hành mà không có bản phát hành nhị phân nào, hoặc nếu bạn cần nhiều kiểm soát hơn về cách Idris được thiết lập.

Để cài đặt, hãy làm theo những bước sau:

Install the Haskell Platform, available from www.haskell.org/downloads.
The Haskell Platform includes a command-line tool, cabal, for installing applications and libraries from the central Hackage repository. Assuming you’re in a Unix-like environment, you can install Idris to an executable at /usr/local/bin/idris with the following commands:
```
$ cabal update $ cabal install idris --program-prefix=/usr/local
```

Editor modes

Trong phần này, tôi sẽ mô tả cách cài đặt chế độ Idris cho việc chỉnh sửa tương tác dựa trên kiểu trong trình soạn thảo văn bản Atom, được sử dụng xuyên suốt cuốn sách này. Tôi cũng sẽ cung cấp cho bạn một số điểm gợi ý về các chế độ trình soạn thảo cho Emacs và Vim.

Atom

Atom có sẵn cho tất cả các nền tảng chính tại http://atom.io/. Bạn có thể cài đặt tiện ích mở rộng để chỉnh sửa các chương trình Idris như sau:

Go to Preferences.
Go to the Install tab.
Search for the language-idris package.
There should be one search result. Click the Install button for this result.
You’ll need to tell the language-idris package where the Idris binary is installed. To do this, first go to the Packages tab.
Click on Settings in the language-idris box.
Under the Settings heading, enter the path where the Idris binary is installed. On this page, you can also change the keyboard shortcuts and various other features.

Other editors

Vào thời điểm viết, chế độ biên tập cũng có sẵn cho Vim và Emacs:

Vim extension—https://github.com/idris-hackers/idris-vim
Emacs mode—https://github.com/idris-hackers/idris-mode

Trong mỗi trường hợp, hướng dẫn cài đặt, cấu hình và sử dụng đều được cung cấp.

Appendix B.
Interactive editing commands

Trong suốt cuốn sách, tôi mô tả việc xây dựng các chương trình Idris tương tác thông qua các lệnh chỉnh sửa trong Atom. Bảng sau tóm tắt các lệnh này để dễ tham khảo.

Table 1.
Interactive editing commands in Atom

Phím tắt	Lệnh	Mô tả
Ctrl-Alt-A	Add definition	Adds a skeleton definition for the name under the cursor
Ctrl-Alt-C	Case split	Splits a definition into pattern-matching clauses for the name under the cursor
Ctrl-Alt-D	Documentation	Displays documentation for the name under the cursor
Ctrl-Alt-L	Lift hole	Lifts a hole to the top level as a new function declaration
Ctrl-Alt-M	Match	Replaces a hole with a case expression that matches on an intermediate result
Ctrl-Alt-R	Reload	Reloads and type-checks the current buffer
Ctrl-Alt-S	Search	Searches for an expression that satisfies the type of the hole name under the cursor
Ctrl-Alt-T	Type-check name	Displays the type of the name under the cursor
Ctrl-Alt-W	with block insertion	Adds a with block after the current line, containing a new pattern-matching clause with an extra argument

Appendix C.
REPL commands

Vòng lặp đọc-đánh giá-in (REPL) của Idris cung cấp một số lệnh để đánh giá và kiểm tra các biểu thức và kiểu dữ liệu, biên dịch chương trình và tìm kiếm tài liệu, cùng với nhiều tính năng khác. Tôi sẽ giới thiệu một số lệnh này trong suốt cuốn sách; bảng dưới đây liệt kê các lệnh được sử dụng phổ biến nhất, nhưng còn nhiều lệnh khác có sẵn. Để biết thêm chi tiết, hãy gõ :? tại REPL.

Table 1.
Idris REPL commands

Lệnh	Lập luận	Mô tả
<expression>	None	Displays the result of evaluating the expression. The variable it contains the result of the most recent evaluation.
:t	<expression>	Displays the type of the expression.
:total	<name>	Displays whether the function with the given name is total.
:doc	<name>	Displays documentation for name.
:let	<definition>	Adds a new definition.
:exec	<expression>	Compiles and executes the expression. If none is given, compiles and executes main.
:c	<output file>	Compiles to an executable with the entry point main.
:r	None	Reloads the current module.
:l	<filename>	Loads a new file.
:module	<module name>	Imports an extra module for use at the REPL.
:printdef	<name>	Displays the definition of name.
:apropos	<word>	Searches function names, types, and documentation for the given word.
:search	<type>	Searches for functions with the given type.
:browse	<namespace>	Displays the names and types defined in the given namespace.
:q	None	Exits the REPL.

Appendix D.
Further reading

Phụ lục này liệt kê một số tài nguyên khác mà bạn có thể tìm hiểu thêm về lập trình hàm, kiểu dữ liệu và các cơ sở lý thuyết của Idris. Các tài nguyên được phân nhóm theo chủ đề, kèm theo một bình luận ngắn về từng tài nguyên.

Functional programming in Haskell

Idris bị ảnh hưởng nặng nề bởi Haskell, bao gồm cú pháp, các tính năng ngôn ngữ và nhiều thư viện chuẩn của nó. Đặc biệt, các giao diện trong Idris có mối liên hệ chặt chẽ với các lớp kiểu của Haskell. Nếu bạn muốn tìm hiểu sâu hơn về Haskell, bạn có thể xem qua những cuốn sách sau:

Learn Haskell by Will Kurt (Manning, 2017) covers Haskell and functional programming concepts, including several practical examples, with particular emphasis on Haskell’s type system.
Programming in Haskell, 2nd ed. by Graham Hutton (Cambridge University Press, 2016) introduces the core features of Haskell and pure functional programming, and it covers many of the more advanced features of Haskell.
Thinking Functionally with Haskell by Richard Bird (Cambridge University Press, 2014) teaches programming from first principles using Haskell, particularly emphasizing techniques for reasoning mathematically about programs.

Other languages and tools with expressive type systems

Nhiều ngôn ngữ khác đã xuất hiện như một kết quả của nghiên cứu học thuật về việc sử dụng loại để lý luận về tính chính xác của chương trình. Đây là một số ví dụ:

Agda (http://wiki.portal.chalmers.se/agda/pmwiki.php)—Supports type-driven development using dependent types in the same way as Idris, but with a stronger emphasis on theorem proving.
F* (www.fstar-lang.org/)—A functional programming language that aims to support program verification using refinement types, which are types augmented with a predicate that describes properties of values in that type.
Coq (https://coq.inria.fr/)—A proof management system based on dependent types with support for extracting functional programs from proofs.

Theoretical foundations

Idris dựa trên nhiều thập kỷ nghiên cứu về lý thuyết loại phụ thuộc. Bạn có thể tìm hiểu thêm về các nền tảng lý thuyết từ các nguồn sau:

Type Theory and Functional Programming by Simon Thompson (Addison Wesley, 1991). This book is now out of print, but it’s available online from the author’s website (www.cs.kent.ac.uk/people/staff/sjt/TTFP/). It provides an accessible introduction to type theory, including its foundations and applications.
Software Foundations by Benjamin Pierce et al. (2016; www.cis.upenn.edu/~bcpierce/sf/current/index.html). This is a course on the mathematical underpinnings of software, from first principles, using Coq. It’s instructive to reproduce the examples in Idris!
Types and Programming Languages by Benjamin Pierce (MIT Press, 2002). This textbook provides a comprehensive introduction to type systems and the basic theory of programming languages.
“Propositions as Types” by Philip Wadler (Communications of the ACM, December 2015; http://cacm.acm.org/magazines/2015/12/194626-propositions-as-types). This paper gives a deep but accessible account of the relationship between logic and programming languages, and in particular the idea that a type in a programming language corresponds to a logical proposition and that a program corresponds to a proof of that proposition.

Total functional programming

Trong suốt cuốn sách này, tôi nói về giá trị của việc viết các hàm tổng quát, và trong chương 10 tôi giới thiệu về các view, cung cấp một cách để viết các hàm tổng quát. Có một số kỹ thuật khác, trong đó một số được mô tả trong các tài liệu sau:

“Elementary Strong Functional Programming” by David Turner (Lecture Notes in Computer Science 1022 (1995):1–13). In this paper, David Turner argues in favor of writing total functions, describing many of the benefits and giving some basic techniques for writing total functions.
“Why Dependent Types Matter” by Thorsten Altenkirch, Conor McBride and James McKinna (2004). This paper, available online (www.cs.nott.ac.uk/~psztxa/publ/ydtm.pdf), describes an earlier dependently typed language, Epigram, emphasizing the importance of totality in dependently typed programming.
“Modelling general recursion in type theory” by Ana Bove and Venanzio Capretta (Mathematical Structures in Computer Science 15 (2005):671–708). Here, the authors describe a way to formalize recursive programs by defining a data type to describe the computational structure of the program.

Types for concurrency

Chương 15 trình bày một cách triển khai các chương trình đồng thời an toàn về kiểu, nhưng nó sử dụng một dạng chương trình đồng thời rất đơn giản. Bạn có thể tìm hiểu thêm về kiểu lập trình đồng thời bằng cách đọc về các kiểu phiên, lần đầu tiên được Kohei Honda mô tả vào năm 1993. Có nhiều nguồn tài liệu, nhưng các bài báo sau đây cung cấp một điểm khởi đầu:

“Types for Dyadic Interaction” by Kohei Honda (Lecture Notes in Computer Science 715 (1993):509–523). This paper introduced the concept of session types, describing a type system for encoding interactions between two processes.
“Multiparty Asynchronous Session Types” by Kohei Honda, Nobuko Yoshida, and Marco Carbone (Principles of Programming Languages, 2008). This paper extends the idea of session types to communicating systems with more than two participants.

Appendix

Vòng lặp đọc - đánh giá - in (REPL) của Idris cung cấp một số lệnh. Các lệnh phổ biến nhất, được liệt kê dưới đây, sẽ được giới thiệu trong suốt cuốn sách này.

Lệnh	Luận cứ	Mô tả
<expression>	None	Displays the result of evaluating the expression. The variable it contains the result of the most recent evaluation.
:t	<expression>	Displays the type of the expression.
:total	<name>	Displays whether the function with the given name is total.
:doc	<name>	Displays documentation for name.
:let	<definition>	Adds a new definition.
:exec	<expression>	Compiles and executes the expression. If none is given, compiles and executes main.
:c	<output file>	Compiles to an executable with the entry point main.
:r	None	Reloads the current module.
:l	<filename>	Loads a new file.
:module	<module name>	Imports an extra module for use at the REPL.
:printdef	<name>	Displays the definition of name.
:apropos	<word>	Searches function names, types, and documentation for the given word.
:search	<type>	Searches for functions with the given type.
:browse	<namespace>	Displays the names and types defined in the given namespace.
:q	None	Exits the REPL.

Appendix

Các lệnh Atom được sử dụng để xây dựng tương tác các dự án Idris được đề cập trong cuốn sách này được chi tiết dưới đây.

Phím tắt	Lệnh	Mô tả
Ctrl-Alt-A	Add definition	Adds a skeleton definition for the name under the cursor
Ctrl-Alt-C	Case split	Splits a definition into pattern-matching clauses for the name under the cursor
Ctrl-Alt-D	Documentation	Displays documentation for the name under the cursor
Ctrl-Alt-L	Lift hole	Lifts a hole to the top level as a new function declaration
Ctrl-Alt-M	Match	Replaces a hole with a case expression that matches on an intermediate result
Ctrl-Alt-R	Reload	Reloads and type-checks the current buffer
Ctrl-Alt-S	Search	Searches for an expression that satisfies the type of the hole name under the cursor
Ctrl-Alt-T	Type-check name	Displays the type of the name under the cursor
Ctrl-Alt-W	with block insertion	Adds a with block after the current line, containing a new pattern-matching clause with an extra argument

Index

[BIỂU TƯỢNG][A][B][C][D][E][F][G][H][I][J][L][M][N][O][P][Q][R][S][T][U][V][W][Z]

SYMBOL

_ (gạch dưới), 2, 3 :: toán tử, 2, 3 :instruct command :r lệnh . hàm /= phương thức, 2 % mặc định tổng chú thích + toán tử ++ toán tử, 2 = kiểu == toán tử, 2, 3 >>= toán tử $ toán tử, 2 $= toán tử

A

hàm vô lý tham số tích lũy Thêm lệnh addCorrect hàm addDownvote hàm adder hàm AdderType hàm addition addPositives hàm addToData hàm addToStore hàm addUpvote hàm addWrong hàm allLengths, tinh chỉnh loại hàm vô danh Cách xử lý Append tập tin AppendVec.idr giao diện Applicative định nghĩa cho State cú pháp do tổng quát bằng cách sử dụng tham số tự động ngầm định định nghĩa hàm với số lượng tham số thay đổi hàm addition hàm printf arithInputs cú pháp số học ví dụ trắc nghiệm số học danh sách vô hạn quy trình vô hạn trạng thái thực thi trắc nghiệm triển khai trắc nghiệm bản ghi lồng cập nhật giá trị trường bản ghi cập nhật các trường bản ghi bằng cách áp dụng hàm ví dụ ATM định nghĩa trạng thái xác định loại cho tinh chỉnh điều kiện tiên quyết bằng cách sử dụng auto-implicits mô phỏng tại console kiểu ATMCmd Nguyên tử lệnh kiểu dữ liệu và mẫu định nghĩa hàm bằng cách sử dụng khớp mẫu từ khóa tự động auto-implicits tổng quan tinh chỉnh điều kiện tiên quyết bằng cách sử dụng

B

- Hàm khởi tạo ràng buộc - Kiểu Bool - Các giá trị Boolean - Các tham số ngầm định ràng buộc - Đóng ngoặc - Các kiểu dữ liệu tích hợp, 2

C

công cụ cabal, Haskell các trình xây dựng chính thống khối case biểu thức case, sử dụng trong kiểu tách case, 2, 3 câu lệnh case hàm cast, 2 Giao diện Cast, chuyển đổi giữa các kiểu với trường hợp catchall thư viện Channels hằng ký tự hàm checkEqNat, 2, 3, 4 trạng thái Closed kiểu Command chú thích mô hình truyền thông các kiểu tổng hợp danh sách hàm với tổng quan bộ dữ liệu lập trình đồng thời kết nối trạng thái Connected các chương trình ConsoleIO hằng số các kiểu tổng quát bị ràng buộc so sánh với Eq và Ord các triển khai bị ràng buộc định nghĩa phương thức mặc định định nghĩa ràng buộc Eq Ord kiểm tra sự bằng nhau với Eq các giao diện được định nghĩa trong Prelude Cast định nghĩa các kiểu số Show các giao diện tham số hóa bởi Type -> Type Foldable Functor Monad và Applicative các kiểu bị ràng buộc luồng điều khiển ràng buộc khớp mẫu tạo ra các giá trị thuần khiết trong các định nghĩa tương tác viết các định nghĩa tương tác với vòng lặp Control.Monad.State, 2 hàm correct lệnh CountFile hàm countFrom, 2 hàm covering, 2 hàm cycle

D

trừu tượng dữ liệu lưu trữ dữ liệu Duyệt nội dung của kho lưu trữ với các chế độ xem Mô-đun Data.List.Views Data.Primitives.Views, 2 kiểu DataStore tinh chỉnh sử dụng bản ghi cho tình trạng chết cứng kiểu Dec hàm decEq khả năng quyết định Dec DecEq biến cố giảm hàm Delay, 2 máy trạng thái phụ thuộc mô tả quy tắc trong kiểu định nghĩa trạng thái trò chơi trừu tượng và các hoạt động định nghĩa trạng thái trò chơi cụ thể định nghĩa kiểu cho trạng thái trò chơi thực hiện trò chơi chạy trò chơi lỗi trong các chuyển đổi trạng thái thuộc tính bảo mật trong kiểu định nghĩa các trạng thái định nghĩa kiểu tinh chỉnh các điều kiện tiên quyết bằng cách sử dụng auto-implicits mô phỏng tại bảng điều khiển các loại phụ thuộc định nghĩa định nghĩa các vector lập chỉ số các vector với các số giới hạn ví dụ phân loại phương tiện đọc và xác thực cặp phụ thuộc đọc các vector từ bảng điều khiển đọc các vector có độ dài không xác định xác thực độ dài vector hàm describeHelper, 2 describeListEnd, 2 DivBy bộ tạo Do từ khóa do cách viết do, 2, 3 mở rộng cho các quy trình vô hạn tuần tự hóa các lệnh với tuần tự hóa các biểu thức với loại Maybe sử dụng Monad và Applicative doAdd hàm doCount ví dụ về các thao tác cửa phát triển tương tác của các chuỗi thao tác mô hình hóa cửa dưới dạng một kiểu đại diện cho lỗi mô tả giao thức cửa đã được xác minh và kiểm tra lỗi trạng thái DoorClosed, 2, 3 kiểu DoorCmd, 2, 3 trạng thái DoorOpen, 2, 3 doorProg, 2 kiểu DoorResult DoorState

E

Thư viện hiệu ứng Cách xác định điều kiện cho phần tử các đối số ngầm định tự động quyết định thành viên của các vectơ đảm bảo một giá trị nằm trong các vectơ loại bỏ các phần tử khỏi Vect, 2 Chế độ Emacs hàm rỗng kiểu rỗng, 2 các loại phân loại, định nghĩa Ràng buộc Eq Giao diện Eq các triển khai có ràng buộc định nghĩa phương thức mặc định định nghĩa bằng cách sử dụng giao diện và triển khai kiểm tra sự bình đẳng Hằng số Eq ty kiểu EqNat, 2 biểu thức bằng nhau các loại bình đẳng quyết định Dec DecEq kiểu rỗng đảm bảo tương đương của dữ liệu với = loại exactLength, 2nd biểu diễn sự bằng nhau của Nats dưới dạng một kiểu manipulating equalities kiểm tra sự bằng nhau của Nats lập luận về sự bằng nhau nối các vectơ ủy quyền chứng minh và viết lại cho các lỗ hổng đảo ngược các vectơ cấu trúc viết lại kiểm tra kiểu và đánh giá hàm equalSuffix evalState hàm exactLength, 2, 3 tệp ExactLength.idr execState bộ sửa đổi xuất khẩu kiểu Expr

F

Loại mặt Giá trị sai filterKeys Tham số kết thúc, lập chỉ mục với số giới hạn Loại hoàn thành tiền tố hữu hạn Các loại bậc nhất định nghĩa các hàm với số lượng tham số thay đổi hàm cộng hàm printf các sơ đồ Loại DataStore hiển thị các mục trong kho lỗ hổng phân tích các mục theo xuất hiện các biểu thức với Maybe sử dụng cú pháp do cập nhật các hàm cấp loại đồng nghĩa loại sử dụng các biểu thức case trong các loại với việc khớp mẫu Giao diện Foldable, giảm cấu trúc bằng cách sử dụng Hàm Force, 2 Hàm forever, 2, 3 Chuỗi định dạng Loại Format Giao diện Fractional Phương thức fromInteger Loại Fuel, 2 Định nghĩa hàm địa phương tổng quan hàm, 2 ẩn danh định nghĩa bằng khớp mẫu định nghĩa với số lượng tham số thay đổi hàm cộng Xuất ra định dạng, một hàm printf an toàn với loại cấp cao hơn định nghĩa địa phương bán phần áp dụng một phần toàn bộ, 2, 3 cấp loại đồng nghĩa loại sử dụng các biểu thức case trong các loại với việc khớp mẫu các loại của hạn chế tổng quan biến trong sử dụng tham số ngầm trong viết tổng quát Giao diện Functor, 2 áp dụng các hàm qua cấu trúc với định nghĩa cho State

G

Loại GameLoop, 2, 3 Trạng thái trò chơi kiểu tổng quát, định nghĩa lấy lệnh Lệnh GetData lấy lệnh nhập Lệnh GetLine, 2 hàm getPrefix, 2 GetRandom Lệnh GetStr getStringOrInt hàm getValues trạng thái toàn cục hàm greet hàm guess ví dụ trò chơi đoán định nghĩa trạng thái trò chơi trừu tượng và các hoạt động định nghĩa trạng thái trò chơi cụ thể định nghĩa loại cho trạng thái trò chơi triển khai chạy

H

Trò chơi đoán từ Hangman Ví dụ hoàn thiện triển khai trò chơi cấp cao Quyết định tính hợp lệ của đầu vào Định nghĩa để xác thực đầu vào của người dùng Xử lý các dự đoán Đại diện cho trạng thái của trò chơi Hàm trò chơi cấp cao Haskell headUnequal hàm phụ trợ Ở đây giá trị không gian tên phân cấp Hàm bậc cao Lỗ hổng sửa lỗi biên dịch bằng cách ủy quyền cho các chứng minh và viết lại cho Homebrew

I

Ngôn ngữ lập trình Idris như một ngôn ngữ lập trình hàm thuần túy hàm tổng quát và hàm riêng biệt tính thuần khiết và tính minh bạch tham chiếu chương trình có tác động bên ngoài kiểm tra kiểu chú thích biên dịch và chạy chương trình kiểu tổng hợp hàm với danh sách danh sách túp lê chế độ trình soạn thảo Atom các trình soạn thảo khác kiểu bậc nhất hàm ẩn danh hàm bậc cao định nghĩa cục bộ áp dụng một phần kiểu và định nghĩa của viết generic với loại bị ràng buộc viết generic với biến trong kiểu lỗ hổng cài đặt biên dịch và môi trường Mac OS nền tảng giống Unix Windows tính tương tác REPL (vòng lặp đọc-đánh giá-in) kiểu Boolean ký tự và chuỗi chuyển đổi số học khoảng trắng tham số ẩn ràng buộc và không ràng buộc nhu cầu cho sử dụng trong các hàm từ khóa không thể Kiểu Inf ty Kiểu Inf, 2 đảm bảo phản hồi bằng cách sử dụng máy trạng thái và biến các quá trình thành tổng quát bằng cách sử dụng danh sách vô hạn ví dụ đố toán học gán nhãn các phần tử trong xử lý sản xuất kiểu dữ liệu Stream hàm tổng quát quá trình vô hạn ví dụ đố toán học miêu tả thực thi mở rộng ký hiệu do cho tạo cấu trúc vô hạn bằng cách sử dụng các kiểu Lazy kiểu InfIO toán tử infix, 2 InfList xử lý đầu vào và đầu ra dòng điều khiển gán kết hợp mẫu sản xuất giá trị thuần túy trong định nghĩa tương tác viết định nghĩa tương tác với vòng lặp kiểu generic IO toán tử >>= ký hiệu do đánh giá và thực thi chương trình tương tác đọc và xác thực các kiểu phụ thuộc cặp phụ thuộc đọc vector từ bảng điều khiển đọc vector có chiều dài không xác định xác thực chiều dài vector hàm đầu vào giao diện Integral cửa hàng dữ liệu tương tác duy trì trạng thái một cách tương tác trong chính phân tích đầu vào người dùng xử lý các lệnh đại diện cho cửa hàng các thao tác tương tác lập trình tương tác dòng điều khiển đọc và xác thực các kiểu phụ thuộc với kiểu generic IO khai báo giao diện các giao diện được định nghĩa trong Prelude Cast định nghĩa các kiểu số Show so sánh generic các thực hiện bị ràng buộc định nghĩa phương thức mặc định định nghĩa Eq bằng cách sử dụng giao diện và thực hiện Ord kiểm tra tính bình đẳng với Eq được tham số hóa bởi Type -> Type Foldable Functor Monad và Applicative hành động IO, 2, 3 IO Hoàn thành kiểu generic IO toán tử >>= ký hiệu do đánh giá và thực thi chương trình tương tác isInt hàm isList hàm isSuffix isValidString, 2 biến it hàm items hàm iterate

J

phương thức join

L

hàm labelFrom hàm labelWith, 2 gói language-idris chú thích lười kiểu lười, tạo ra các cấu trúc vô hạn bằng cách sử dụng phép toán độ dài cho phép xây dựng bộ phát sinh đồng dư tuyến tính Danh sách Char Danh sách elem lắng nghe ListLast, 2 các hàm danh sách với việc khớp mục cuối cùng trong quá trình đảo ngược snoc hàm ListType trạng thái có thể thay đổi cục bộ trạng thái cục bộ hàm logOpen biến xây dựng Loop hàm loopPrint, 2 vòng lặp, viết các định nghĩa tương tác với

M

MáyCmd, 2 hàm chính duy trì trạng thái một cách tương tác trong hàm chính tổng quan, 2 hàm ánh xạ các ma trận phép toán liên quan đến các hàm, các phép toán và kiểu, chuyển vị Loại đối tượng Có thể elemen Loại có thể, sử dụng cú pháp do hàm maybeAdd các bài kiểm tra thành viên, các tham số ẩn tự động, xác định thành viên của các véc tơ, đảm bảo một giá trị nằm trong các véc tơ, loại bỏ các phần tử khỏi Vect, 2 sắp xếp hòa trộn hàm mergeSort, 2, 3 MessagePID khai báo phương thức MkData đối số MkWordState các mô-đun, trong Idris giao diện Monad xác định cho State, cú pháp do tổng quát sử dụng giao diện MonadState trạng thái có thể thay đổi, đại diện bằng các cặp, loại State, ví dụ xuyên qua cây, xuyên qua cây với State khối tương hỗ hàm myReverse, 2 hàm myReverseHelper

N

tên miền Nats biểu thị sự bình đẳng của như một loại tổng quan, 2, 3 kiểm tra sự bình đẳng của giao diện Neg trạng thái kế tiếp constructor Nil các chương trình không xác định thành phần không kết thúc hàm noRec giao diện NoRecv trạng thái NoRequest không có trong Nil không có trong đuôi trạng thái NotRunning giao diện Num numargs các loại và giá trị số định nghĩa

O

hàm occurrences Giao diện Ord xác định các thứ tự với tổng quan, 2

P

cặp, đại diện cho trạng thái có thể thay đổi hàm đối xứng loại tham số hóa phân tích theo lược đồ phân tích lệnh, 2 phân tích tiền tố hàm từng phần ứng dụng một phần của các hàm khớp mẫu mở rộng bằng các kiểu nhìn, trừu tượng dữ liệu định nghĩa và sử dụng kiểu nhìn khám phảit kiểu nhìn đệ quy cú pháp cho mở rộng hàm cấp kiểu với ràng buộc khớp mẫu PID (định danh quá trình) hàm cộng loại cộng giao hoán plusSuccRightSucc plusZeroRightNeutral hàm Đa giác hàm Vị trí điều kiện điều kiện Elem tham số tự động ẩn quyết định thành viên của vector đảm bảo một giá trị có trong các vector xóa phần tử khỏi Vect, 2nd ví dụ trò chơi đoán Hangman hoàn tất triển khai trò chơi cấp cao quyết định tính hợp lệ của đầu vào điều kiện để xác thực đầu vào của người dùng xử lý các lần đoán đại diện cho trạng thái của trò chơi hàm trò chơi cấp cao các nguyên thủy, cho lập trình đồng thời thư viện Kênh định nghĩa các quy trình đồng thời lỗi kiểu và chặn hàm printf, 2, 3 PrintfType printLn, 2 lĩnh vực vấn đề procAdder định danh quá trình. Xem PID. quá trìnhNhập module ProcessLib procMain, 2 ProcState xuất công khai bộ tạo thuần khiết, 2 hàm thuần khiết ngôn ngữ lập trình hàm thuần khiết các hàm từng phần và tổng quát tính thuần khiết tính minh bạch tham chiếu các chương trình có tác dụng phụ. Xem thêm ngôn ngữ lập trình Idris. tính thuần khiết lệnh PutStr, 2, 3

Q

Lệnh thoát chức năng đố vui, 2, 3, 4

R

điều kiện cạnh tranh hàm ngẫu nhiên, 2 hoạt động đọc hàm readGuess readInput, 2 khai báo bản ghi đệ quy định nghĩa kiểu đệ quy cái nhìn đệ quy module Data.List.Views lồng với khối danh sách snoc với cấu trúc tính minh bạch tham chiếu Refl (phản xạ) hàm removeElem hàm repeat REPL (vòng lặp đọc-đánh giá-in), 2 hàm repl Lệnh Respond trả về giá trị hàm reverse cấu trúc rewrite, 2, 3 rewriteCons rewriteNil hoạt động RingBell hàm run, 2, 3, 4, 5 runCommand, 2 kiểu RunIO Trạng thái đang chạy runProc hàm runState, 2, 3, 4, 5

S

chức năng sameS, 2 lược đồ sửa lỗi biên dịch bằng cách sử dụng lỗ trống loại DataStore tinh chỉnh sử dụng bản ghi để hiển thị các mục trong kho tổng quan phân tích các mục theo sắp xếp biểu thức với Maybe sử dụng cú pháp do cập nhật chức năng SchemaType, 2 trạng thái gửi setDifficulty lệnh SetSchema loại hình dạng chức năng show Giao diện Show, chuyển đổi sang String với chức năng showPrec ShowState các chương trình có tác dụng phụ chức năng size chức năng sort sắp xếp vectơ spawn SplitList SplitNil SplitOne SplitRec SplitRecPair ví dụ máy tính dựa trên ngăn xếp StackCmd, 2 ngăn xếp triển khai bằng cách sử dụng Vect đại diện cho các phép toán ví dụ máy tính dựa trên ngăn xếp trạng thái quiz số học định nghĩa bản ghi lồng nhau thực thi triển khai cập nhật giá trị trường bản ghi cập nhật trường bản ghi bằng cách áp dụng các hàm cài đặt tùy chỉnh của xác định Functor, Applicative và Monad giao diện xác định State và runState trạng thái có thể thay đổi đại diện bằng cặp loại State ví dụ duyệt cây duyệt cây với State máy trạng thái phụ thuộc mô tả quy tắc trong các loại lỗi trong các chuyển tiếp trạng thái các thuộc tính bảo mật trong các loại đảm bảo phản hồi bằng cách sử dụng Inf và triển khai ngăn xếp đại diện cho các phép toán ví dụ máy tính dựa trên ngăn xếp sử dụng Vect theo dõi trạng thái trong các loại ví dụ hoạt động cửa ra vào ví dụ máy bán hàng, phần thứ 2 Kiểu State Nat ty Loại State định nghĩa duyệt cây với hàm storeView cái nhìn StoreView kiểu dữ liệu Stream loại Stream dòng, danh sách vô hạn ví dụ quiz số học gán nhãn các phần tử trong xử lý sản xuất loại dữ liệu Stream các hàm tổng hợp chuỗi ký tự StringOrInt, 2 strToInput chức năng sucNotZero module Hệ thống module System.Concurrency.Channels, 2

T

- không bằng nhau - hàm take - hàm takeN - kết thúc lệnh theo miền cụ thể lệnh sắp xếp với ký hiệu do - testAdd - testStore - testTree - Hàm khởi tạo - kiểu ThreeEq - hàm thời gian - hàm toBinary - hàm tổng quát thực hiện các quá trình vô hạn như tổng quan, 2 - totalREPL - hàm duyệt - kiểu dữ liệu Cây - phần tử cây - hàm treeLabel - treeLabelWith - ví dụ duyệt cây tổng quan với State - hàm trim - giá trị True - lệnh Try - bộ - kiểu TupleVect - Giao diện tham số hóa kiểu -> Kiểu áp dụng hàm trên cấu trúc với Functor ký hiệu do tổng quát sử dụng Monad và Applicative giảm cấu trúc sử dụng Foldable - từ đồng nghĩa kiểu - kiểm tra kiểu - phát triển điều khiển bởi kiểu ví dụ máy rút tiền tự động lập trình đồng thời kiểu phụ thuộc ma trận, phép toán liên quan quá trình khái niệm kiểu, được định nghĩa - hàm cấp độ kiểu - kiểu Booleans tính toán từ đồng nghĩa kiểu hàm cấp độ kiểu với khớp mẫu sử dụng biểu thức case trong kiểu ký tự và chuỗi kiểm tra kiểm tra và đánh giá của tổ hợp danh sách bộ generic có ràng buộc so sánh với Eq và Ord giao diện được định nghĩa trong Prelude giao diện được tham số hóa bởi Kiểu -> Kiểu chuyển đổi được định nghĩa phụ thuộc mô tả quy tắc trong định nghĩa trạng thái trò chơi trừu tượng và các thao tác định nghĩa trạng thái trò chơi cụ thể định nghĩa kiểu cho trạng thái trò chơi triển khai trò chơi chạy trò chơi rỗng bằng nhau khả quyết định kiểu rỗng đảm bảo tính tương đương của dữ liệu với lập luận về tính bằng nhau cấp một định nghĩa hàm với số lượng tham số biến đổi lược đồ hàm cấp độ kiểu hàm có ràng buộc biến trong trong Atom số, 2 thuộc tính bảo mật trong định nghĩa các trạng thái định nghĩa kiểu làm tinh chỉnh điều kiện tiên quyết sử dụng auto-implicits mô phỏng tại bảng điều khiển theo dõi trạng thái trong ví dụ thao tác cửa ví dụ máy bán hàng, lần thứ 2 do người dùng định nghĩa định nghĩa định nghĩa phụ thuộc cửa hàng dữ liệu tương tác - lập trình đồng thời an toàn theo kiểu các nguyên thủy cho thư viện Channels định nghĩa các quá trình đồng thời lỗi kiểu và chặn kiểu cho việc truyền tin an toàn định nghĩa mô-đun mô tả các quá trình các quá trình tổng quát đảm bảo phản hồi sử dụng máy trạng thái và Inf ví dụ xử lý danh sách làm cho các quá trình tổng quát sử dụng Inf ví dụ quá trình đếm từ

U

các tham số ngầm định không ràng buộc gạch dưới (_), 2, 3 giao diện không có phần tử các kiểu hợp nhất, định nghĩa unsafeReceive unsafeSend, 2 hàm updateGameState các kiểu dữ liệu do người dùng định nghĩa định nghĩa các kiểu liệt kê các kiểu tổng quát các kiểu đệ quy các kiểu hợp nhất định nghĩa phụ thuộc định nghĩa vector lập chỉ mục vector với các số giới hạn ví dụ phân loại phương tiện kho dữ liệu tương tác duy trì trạng thái một cách tương tác trong main phân tích đầu vào của người dùng xử lý lệnh đại diện cho kho dữ liệu

V

Định nghĩa predicate ValidInput quyết định tính hợp lệ của đầu vào tổng quan valToString Kích thước Vect Chuỗi Loại Vect, triển khai ngăn xếp bằng cách sử dụng vectors thêm vào tự động tinh chỉnh quyết định thành viên của định nghĩa đảm bảo một giá trị nằm trong lập chỉ mục với các số có giới hạn sử dụng Fin đọc từ console có độ dài không xác định tinh chỉnh loại của hàm allLengths loại bỏ các phần tử từ, 2 đảo ngược sắp xếp xác thực độ dài ví dụ máy bán hàng mô hình máy bán hàng mô tả đã xác minh các khung nhìn trừu tượng dữ liệu kho dữ liệu mô-đun trong Idris duyệt nội dung của kho định nghĩa và sử dụng xây dựng các khung nhìn khớp phần tử cuối cùng trong danh sách sắp xếp gộp đảo ngược danh sách với các khối đệ quy mô-đun Data.List.Views lồng với các khối danh sách snoc với cấu trúc phần mở rộng Vim Khung nhìn VList Kiểu Void kiểu rỗng tổng quan, 2

W

WCData dịch vụ wc khi hàm nơi cấu trúc khoảng trắng với các khối lồng ghép tổng quan cú pháp cho việc khớp mẫu mở rộng với cấu trúc, 2 kiểu WordState, 2 hoạt động ghi hàm sai

Z

Hàm zeroNotSuc zipInputs

List of Figures

Chương 1. Tổng quan

Hình 1.1. Đỉnh của một đồ chơi phân loại hình dạng. Các hình dạng tương ứng với các loại đồ vật sẽ vừa với các lỗ.

Hình 1.2. Các trạng thái và các thao tác hợp lệ trên một máy ATM. Mỗi thao tác chỉ hợp lệ trong các trạng thái cụ thể và có thể thay đổi trạng thái của máy. CheckPIN chỉ thay đổi trạng thái nếu mã PIN nhập vào là chính xác.

Hình 1.3. Hai quá trình đồng thời tương tác, chính và bộ cộng. Quá trình chính gửi một yêu cầu đến bộ cộng, sau đó bộ cộng gửi phản hồi trở lại cho quá trình chính.

Hình 1.4. Một hàm thuần khiết, nhận đầu vào và tạo ra đầu ra mà không có tác dụng phụ nào quan sát được

Hình 1.5. Các hàm thuần túy, nói chung, chỉ nhận đầu vào và không có tác động phụ có thể quan sát được.

Hình 1.6. Một chương trình có tác dụng phụ, đọc đầu vào từ một tệp, in kết quả và trả về kết quả.

Chương 2. Bắt đầu với Idris

Hình 2.1. Các thành phần của một định nghĩa hàm

Hình 2.2. Định nghĩa một biến cục bộ: trong biểu thức sau từ khóa in, x có giá trị là 50.

Chương 3. Phát triển tương tác với kiểu dữ liệu

Hình 3.1. Khớp mẫu (x :: xs) cho các đầu vào [1] và [2,3,4,5]

Hình 3.2. Tính toán độ dài của các từ trong một danh sách. Lưu ý rằng mỗi đầu vào có một đầu ra tương ứng, vì vậy độ dài của vector đầu ra luôn bằng với độ dài của vector đầu vào.

Hình 3.3. Đại diện của một ma trận dưới dạng các vectơ hai chiều. Bên trái, ma trận được thể hiện bằng ký hiệu toán học. Ma trận giống hệt được biểu diễn trong Idris bên phải.

Hình 3.4. Các thành phần của vector bạn đang chuyển vị (x và xs), cùng với kết quả của việc chuyển vị xs, và kết quả tổng thể mong đợi.

Chương 4. Kiểu dữ liệu do người dùng định nghĩa

Hình 4.1. Định nghĩa kiểu dữ liệu Hướng (Direction.idr)

Hình 4.2. Các hình dạng được đại diện dưới dạng kiểu hợp nhất. Hình tam giác nhận hai số thực, cho cạnh đáy và chiều cao; Hình chữ nhật nhận hai số thực, cho chiều rộng và chiều cao; Hình tròn nhận một số thực cho bán kính.

Hình 4.3. Một hình ảnh ví dụ kết hợp ba hình dạng được dịch chuyển đến các vị trí khác nhau.

Hình 4.4. Định nghĩa kiểu dữ liệu Either

Hình 4.5. Ghép các phần tử tương ứng của [1,2,3,4] và ["one","two","three","four"] bằng cách sử dụng zip

Chương 5. Chương trình tương tác: xử lý đầu vào và đầu ra

Hình 5.1. Đánh giá biểu thức putStrLn (show (47 * 2)) và sau đó thực thi các hành động kết quả.

Hình 5.2. Một thao tác tương tác để đọc một chuỗi và sau đó phản hồi nội dung của nó bằng cách sử dụng toán tử >>=. Các kiểu của mỗi biểu thức con được chỉ ra.

Hình 5.3. Biến đổi cú pháp do thành biểu thức sử dụng toán tử >>= khi sắp xếp các hành động. Giá trị được tạo ra bởi hành động, kiểu ty, bị bỏ qua, như được chỉ ra bởi dấu gạch dưới.

Hình 5.4. Chuyển đổi cú pháp do thành biểu thức sử dụng toán tử >>= khi ràng buộc một biến và tuần tự thực hiện các hành động.

Hình 5.5. Cú pháp của cặp phụ thuộc. Lưu ý rằng phần tử đầu tiên được đặt tên, có thể được sử dụng trong kiểu của phần tử thứ hai.

Chương 6. Lập trình với các kiểu dữ liệu hạng nhất

Hình 6.1. Hành vi của một hàm cộng với số lượng tham số biến đổi

Hình 6.2. Hành vi của hàm printf với các chuỗi định dạng khác nhau

Hình 6.3. Dịch một chuỗi định dạng thành mô tả định dạng

Hình 6.4. Hai kho dữ liệu khác nhau, với các sơ đồ khác nhau. Sơ đồ 1 yêu cầu dữ liệu có kiểu (Int, String), và sơ đồ 2 yêu cầu dữ liệu có kiểu (String, String, Int).

Hình 6.5. Chuyển đổi ký hiệu do sang biểu thức sử dụng toán tử (>>=)

Chương 7. Giao diện: sử dụng kiểu tổng quát hạn chế

"Hình 7.1. Khai báo giao diện Eq"

Hình 7.2. Tiêu đề thực hiện có ràng buộc

Hình 7.3. Gập cây con bên trái với bộ tích lũy ban đầu. Điều này cho bạn 0 + 1 + 2 + 3 = 6.

Hình 7.4. Gập nhánh bên phải, khởi tạo với kết quả của việc gập nhánh bên trái. Điều này cho bạn 6 + 5 + 6 + 7 = 24.

Chương 8. Bình đẳng: biểu thị mối quan hệ giữa các dữ liệu

Hình 8.1. Viết lại một kiểu bằng chứng bình đẳng

Chương 10. Các chế độ xem: mở rộng việc ghép mẫu

Hình 10.1. Khớp mẫu (x :: xs) cho các đầu vào [1] và [2,3,4,5]

Hình 10.2. Khớp mẫu (xs ++ [x]) cho các đầu vào [1] và [2,3,4,5]

Hình 10.3. Cú pháp cho cấu trúc with

Hình 10.4. Sắp xếp một danh sách bằng cách sử dụng thuật toán sắp xếp hợp nhất: chia danh sách thành hai nửa, sắp xếp hai nửa, và sau đó hợp nhất các nửa đã sắp xếp lại với nhau.

Chương 11. Dòng và quy trình: làm việc với dữ liệu vô hạn

Hình 11.1. Gán nhãn các phần tử của một danh sách bằng cách lấy các phần tử từ một luồng số vô hạn. Luồng chứa một số lượng phần tử vô hạn, nhưng bạn chỉ lấy bao nhiêu phần tử cần thiết để gán nhãn cho các phần tử trong danh sách hữu hạn.

Hình 11.2. Tạo ra các giá trị của một cấu trúc vô hạn. Sự Trì hoãn có nghĩa là Idris chỉ thực hiện cuộc gọi đệ quy đến countFrom khi nó được yêu cầu bởi Force.

Hình 11.3. Biến đổi cú pháp do thành biểu thức sử dụng toán tử >>= khi sắp xếp các hành động

Chương 12. Viết chương trình với trạng thái

Hình 12.1. Gán nhãn cho một cây, theo chiều sâu. Mỗi nút được gán nhãn bằng một số nguyên.

Hình 12.2. Gán nhãn các cây con. Cây con bên trái được gán nhãn từ 1 đến 3, và cây con bên phải được gán nhãn từ 5 đến 6.

Hình 12.3. Cú pháp để trả về một bản ghi mới với một trường được cập nhật.

Chương 13. Máy trạng thái: xác minh giao thức trong kiểu dữ liệu

Hình 13.1. Một sơ đồ chuyển trạng thái cho thấy hoạt động cấp cao của một cơ sở dữ liệu. Nó có hai trạng thái khả thi, Đóng và Kết nối. Ba hoạt động của nó, Kết nối, Truy vấn và Đóng, chỉ hợp lệ trong những trạng thái cụ thể.

Hình 13.2. Một sơ đồ chuyển trạng thái cho thấy các trạng thái và hoạt động trên một cánh cửa

Hình 13.3. Cách mà mỗi đầu vào của người dùng ảnh hưởng đến nội dung của ngăn xếp

Chương 14. Máy trạng thái phụ thuộc: xử lý phản hồi và lỗi

Hình 14.1. Sơ đồ chuyển trạng thái mô tả các trạng thái và hoạt động của một cánh cửa.

Hình 14.2. Một sơ đồ chuyển trạng thái hiển thị các trạng thái và hoạt động trên một cánh cửa, trong đó việc mở cửa có thể thất bại.

Hình 14.3. Loại mới cho DoorCmd, trong đó trạng thái đầu ra của một thao tác được tính toán từ giá trị trả về của thao tác.

Hình 14.4. Một máy trạng thái mô tả các trạng thái và hoạt động trên một máy ATM. Điều này bỏ qua các hoạt động (như GetAmount) có giá trị trong tất cả các trạng thái.

Hình 14.5. Sơ đồ chuyển trạng thái cho trò chơi Đoán chữ. Trạng thái Đang chạy cũng ghi lại số lượng chữ cái và số lần đoán còn lại. Trạng thái Thắng yêu cầu số lượng chữ cái phải bằng không, và trạng thái Thua yêu cầu số lần đoán phải bằng không.

Chương 15. Lập trình đồng thời an toàn kiểu dữ liệu

Hình 15.1. Giả thuyết mã cho khách hàng và máy chủ, trong đó mỗi tiến trình đọc và ghi một biến chia sẻ, var. Điều này có thể dẫn đến kết quả không mong đợi nếu dòng A và C được thực hiện trước dòng C và D.

Hình 15.2. Truyền thông điệp giữa các tiến trình. Một tiến trình chính gửi một thông điệp Cộng 2 3 đến một tiến trình cộng, và nó trả lời bằng cách gửi một thông điệp 5 trở lại tiến trình chính.

Hình 15.3. Một sơ đồ chuyển trạng thái cho thấy các trạng thái và hoạt động trong một quy trình máy chủ. Một quy trình bắt đầu ở trạng thái NoRequest và phải kết thúc ở trạng thái Complete, có nghĩa là nó đã phản hồi ít nhất một yêu cầu.

Hình 15.4. Một loại quy trình tinh chỉnh, bao gồm giao diện mà quy trình phản hồi như là một phần của loại này.

List of Tables

Chương 1. Tổng quan

Bảng 1.1. Các loại đầu vào và đầu ra cho các phép toán ma trận. Các tên x, y và z mô tả, chung chung, cách mà các kích thước của đầu vào và đầu ra liên quan đến nhau.

Bảng 1.2. Thêm các danh sách kiểu cụ thể. Khác với các kiểu đơn giản, nơi không có sự khác biệt giữa các kiểu danh sách đầu vào và đầu ra, các kiểu phụ thuộc cho phép chiều dài được mã hóa trong kiểu.

Bảng 1.3. Thêm danh sách kiểu, nói chung. Biến kiểu mô tả các mối quan hệ giữa các đầu vào và đầu ra, mặc dù các đầu vào và đầu ra chính xác không được biết đến.

Chương 3. Phát triển tương tác với kiểu dữ liệu

Bảng 3.1. Các lệnh chỉnh sửa tương tác trong Atom

Chương 7. Giao diện: sử dụng loại tổng quát có ràng buộc

Bảng 7.1. Tóm tắt các giao diện số và các triển khai của chúng

Chương 13. Máy trạng thái: xác minh các giao thức trong kiểu dữ liệu

Bảng 13.1. Hoạt động máy bán hàng tự động, với trạng thái đầu vào và đầu ra được biểu diễn dưới dạng Nat

Bảng 13.2. Các thao tác ngăn xếp, với kích thước ngăn xếp đầu vào và đầu ra được biểu diễn dưới dạng Nat.

Chương 15. Lập trình đồng thời an toàn kiểu dữ liệu

Bảng 15.1. Giá trị của var cho mỗi chuỗi thao tác trong hình 15.1, với giá trị ban đầu là 1 cho var

Phụ lục B. Các lệnh chỉnh sửa tương tác

Bảng 1. Các lệnh chỉnh sửa tương tác trong Atom

Phụ lục C. Lệnh REPL

Bảng 1. Lệnh REPL Idris

List of Listings

Chương 1. Tổng quan

Danh sách 1.1. Nối các danh sách được đọc từ một tệp (mã giả)

Danh sách 1.2. Xin chào, thế giới Idris! (Hello.idr)

Danh sách 1.3. Một chương trình có lỗi kiểu

Danh sách 1.4. Tính toán một kiểu, cho một giá trị Boolean (FCTypes.idr)

Chương 2. Bắt đầu với Idris

Danh sách 2.1. Một chương trình Idris hoàn chỉnh để tính toán độ dài trung bình của từ (Average.idr)

Danh sách 2.2. Một hàm để gấp đôi một số nguyên (Double.idr)

Danh sách 2.3. Một kiểu tổng quát, bị ràng buộc cho các kiểu số (Generic.idr)

Danh sách 2.4. Định nghĩa bốn phần và xoay bằng cách sử dụng hàm bậc cao (HOF.idr)

Danh sách 2.5. Biến cục bộ với let (Let_Where.idr)

Danh sách 2.6. Định nghĩa hàm cục bộ với where (Let_Where.idr)

Danh sách 2.7. Tính toán độ dài trung bình của từ trong một chuỗi (Average.idr)

Danh sách 2.8. Quy tắc bố trí áp dụng cho trung bình (Average.idr)

Danh sách 2.9. Quy tắc bố trí, được áp dụng không chính xác

Danh sách 2.10. Đảo ngược chuỗi tương tác (Reverse.idr)

Danh sách 2.11. Hiển thị chiều dài trung bình của các từ một cách tương tác (AveMain.idr)

Chương 3. Phát triển tương tác với kiểu dữ liệu

Danh sách 3.1. Tính toán độ dài của từ bằng cách khớp mẫu trên danh sách (WordLength.idr)

Danh sách 3.2. Vectors: danh sách với độ dài được mã hóa trong kiểu (Vectors.idr)

Danh sách 3.3. Một định nghĩa khung của insSort trên các vector với loại khởi đầu (VecSort.idr)

Danh sách 3.4. Định nghĩa đầy đủ về phép chuyển vị ma trận (Matrix.idr)

Chương 4. Các kiểu dữ liệu do người dùng định nghĩa

Danh sách 4.1. Các loại và bộ tạo dữ liệu từ :doc

Danh sách 4.2. Định nghĩa loại Hình và tính diện tích của nó (Shape.idr)

Danh sách 4.3. Xác định một loại Hình ảnh một cách đệ quy, bao gồm các Hình dạng và các Hình ảnh nhỏ hơn (Picture.idr)

Danh sách 4.4. Hình ảnh từ hình 4.3 được thể hiện bằng mã (Picture.idr)

Danh sách 4.5. Tính tổng diện tích của tất cả các hình trong một Bức tranh (Picture.idr)

Danh sách 4.6. Một kiểu chung, Maybe, nắm bắt khả năng thất bại.

Liệt kê 4.7. Định nghĩa cây nhị phân (Tree.idr)

Danh sách 4.8. Chèn một giá trị vào cây tìm kiếm nhị phân (Tree.idr)

Danh sách 4.9. Một cây tìm kiếm nhị phân với ràng buộc sắp xếp trong loại (BSTree.idr)

Danh sách 4.10. Định nghĩa một loại phụ thuộc cho các phương tiện, với nguồn năng lượng của chúng trong loại (vehicle.idr)

Danh sách 4.11. Đọc và cập nhật thuộc tính của Xe cộ

Danh sách 4.12. Định nghĩa vector (Vect.idr)

Danh sách 4.13. Triển khai tổng quan của kho dữ liệu (DataStore.idr)

Danh sách 4.14. Một loại dữ liệu để đại diện cho kho dữ liệu (DataStore.idr)

Danh sách 4.15. Dự đoán kích thước và nội dung của một kho dữ liệu (DataStore.idr)

Danh sách 4.16. Thêm một mục mới vào kho dữ liệu (DataStore.idr)

Danh sách 4.17. Chương trình tương tác để tính tổng các giá trị đầu vào cho đến khi một giá trị âm được đọc (SumInputs.idr)

Danh sách 4.18. Phân tích một chuỗi lệnh và tham số thành một Lệnh (DataStore.idr)

Danh sách 4.19. Xử lý các đầu vào Thêm mục và Thoát (DataStore.idr)

Danh sách 4.20. Triển khai đầy đủ của một kho dữ liệu đơn giản (DataStore.idr)

Chương 5. Các chương trình tương tác: xử lý đầu vào và đầu ra

Danh sách 5.1. Một chương trình tương tác đơn giản, đọc tên của người dùng và hiển thị lời chào (Hello.idr)

Danh sách 5.2. Một hàm để hiển thị một lời nhắc, đọc một chuỗi, và sau đó hiển thị độ dài của nó, sử dụng >>= để tuần tự hóa các hành động IO (PrintLength.idr)

Danh sách 5.3. Một hàm để hiển thị một thông báo, đọc một chuỗi, và sau đó hiển thị độ dài của nó bằng cách sử dụng cú pháp do để tuần tự hóa các hành động IO (PrintLength.idr)

Danh sách 5.4. Đọc và xác thực một số (ReadNum.idr)

Danh sách 5.5. Đọc và xác thực một cặp số từ bảng điều khiển (ReadNum.idr)

Danh sách 5.6. Đọc và xác thực một cặp số từ bảng điều khiển, ngắn gọn (ReadNum.idr)

Danh sách 5.7. Hiển thị một đồng hồ đếm ngược, tạm dừng một giây giữa mỗi lần lặp lại (Loops.idr)

Danh sách 5.8. Tiếp tục đếm ngược cho đến khi người dùng không muốn chạy nữa (Loops.idr)

Danh sách 5.9. Đọc một Vect có độ dài đã biết từ bảng điều khiển (ReadVect.idr)

Danh sách 5.10. Đọc một Vect có độ dài không xác định từ bảng điều khiển (ReadVect.idr)

Danh sách 5.11. Đọc một Vect có độ dài không xác định từ bảng điều khiển, trả về một cặp phụ thuộc (DepPairs.idr)

Danh sách 5.12. Định nghĩa hoàn chỉnh của zipInputs (DepPairs.idr)

Chương 6. Lập trình với các kiểu bậc nhất

Danh sách 6.1. Định nghĩa một đa giác bằng cách sử dụng đồng nghĩa kiểu (TypeSynonym.idr)

Danh sách 6.2. Một hàm tính toán một kiểu từ một Bool (TypeFuns.idr)

Danh sách 6.3. Một hàm để tính toán kiểu cho bọ cộng n (Adder.idr)

Danh sách 6.4. Một bộ cộng tổng quát hoạt động cho bất kỳ kiểu số nào (Adder.idr)

Danh sách 6.5. Đại diện cho chuỗi định dạng dưới dạng kiểu dữ liệu (Printf.idr)

Danh sách 6.6. Tính toán kiểu của printf từ một chỉ định định dạng (mở rộng Printf.idr)

Danh sách 6.7. Hàm trợ giúp cho printf, xây dựng một chuỗi từ một định dạng (Printf.idr)

Danh sách 6.8. Định nghĩa cấp cao của printf, với một chuyển đổi từ String sang Format (Printf.idr)

Bảng 6.9. Phác thảo của loại DataStore đã được tinh chỉnh, với mô tả Schema và việc dịch Schema sang các loại cụ thể đều chưa được xác định (DataStore.idr)

Danh sách 6.10. Định nghĩa Lược đồ và chuyển đổi Lược đồ sang kiểu cụ thể

Danh sách 6.11. Triển khai DataStore dưới dạng một bản ghi, với các chức năng chiếu được tự động tạo.

Danh sách 6.12. Một định nghĩa đã được sửa đổi của addToStore sử dụng kiểu DataStore đã tinh chỉnh.

Danh sách 6.13. Phiên bản cũ của getEntry, với lỗi trong việc áp dụng chỉ số

Danh sách 6.14. Sửa đổi getEntry bằng cách chèn một lỗ để chuyển đổi nội dung của kho thành một chuỗi có thể hiển thị.

Danh sách 6.15. Phiên bản cũ của processInput, với lỗi trong việc áp dụng addToStore.

Danh sách 6.16. Lệnh, được tinh chỉnh để được tham số hóa bởi sơ đồ trong kho dữ liệu.

Danh sách 6.17. Cập nhật parseCommand để phân tích cú pháp các đầu vào tuân theo sơ đồ

Danh sách 6.18. Cập nhật processInput và main, với một schema mặc định

Danh sách 6.19. Triển khai tóm tắt của parseBySchema, sử dụng một hàm parsePrefix chưa được định nghĩa để phân tích một tiền tố của đầu vào theo một sơ đồ.

Danh sách 6.20. Phân tích một tiền tố của đầu vào theo một lược đồ cụ thể

Danh sách 6.21. Cấu trúc dữ liệu Lệnh với một lệnh mới để cập nhật sơ đồ

Danh sách 6.22. Phân tích mô tả Schema và mở rộng trình phân tích cho Lệnh để hỗ trợ thiết lập một schema mới.

Danh sách 6.23. Xử lý lệnh SetSchema, cập nhật mô tả schema trong DataStore

Danh sách 6.24. Thêm hai Maybe Ints (Maybe.idr)

Danh sách 6.25. Thêm hai Maybe Ints bằng cách sử dụng (>>=) thay vì phân tích trường hợp trực tiếp.

Danh sách 6.26. Thêm hai Maybe Ints bằng cách sử dụng cú pháp do thay vì sử dụng (>>=) trực tiếp.

Chương 7. Giao diện: sử dụng các loại tổng quát có ràng buộc

Danh sách 7.1. Giao diện Eq (được định nghĩa trong Prelude)

Danh sách 7.2. Triển khai Eq cho Vật chất (Eq.idr)

Danh sách 7.3. Giao diện Eq với định nghĩa phương thức mặc định

Danh sách 7.4. Giao diện Ord, mở rộng Eq (được định nghĩa trong Prelude)

Danh sách 7.5. Một kiểu dữ liệu bản ghi và một tập hợp để được sắp xếp (Ord.idr)

Danh sách 7.6. Triển khai Eq và Ord cho Album

Danh sách 7.7. Giao diện Show (được định nghĩa trong Prelude)

Danh sách 7.8. Hệ thống phân cấp giao diện số (được định nghĩa trong Prelude)

Danh sách 7.9. Một kiểu dữ liệu biểu thức số học và một bộ đánh giá (Expr.idr)

Danh sách 7.10. Các triển khai của Num và Neg cho Expr (Expr.idr)

Danh sách 7.11. Giao diện Cast (được định nghĩa trong Prelude)

Danh sách 7.12. Giao diện Functor và một triển khai cho List (được định nghĩa trong Prelude)

Danh sách 7.13. Triển khai Functor cho Cây (Tree.idr)

Danh sách 7.14. Triển khai Functor cho vectơ (được định nghĩa trong Data.Vect)

Danh sách 7.15. Giao diện Foldable (được định nghĩa trong Prelude)

Danh sách 7.16. Triển khai Foldable cho List (được định nghĩa trong Prelude)

Danh sách 7.17. Giao diện Monad (được định nghĩa trong Prelude)

Danh sách 7.18. Giao diện Applicative (được định nghĩa trong Prelude)

Chương 8. Bình đẳng: diễn đạt mối quan hệ giữa dữ liệu

Danh sách 8.1. Một định nghĩa về Vect và định nghĩa kiểu và khung của exactLength (ExactLength.idr)

Danh sách 8.2. Đại diện cho các số tự nhiên bằng nhau dưới dạng một kiểu (EqNat.idr)

Danh sách 8.3. Kiểm tra tính bằng nhau của các số tự nhiên với EqNat (EqNat.idr)

Danh sách 8.4. Định nghĩa khái niệm của một loại bình đẳng tổng quát

Danh sách 8.5. Kiểm tra sự bình đẳng giữa Nats bằng cách sử dụng kiểu bình đẳng tổng quát (CheckEqMaybe.idr)

Liệt kê 8.6. Triển khai hàm append trên các vector với các đối số của + được hoán đổi trong kiểu trả về (AppendVec.idr)

Liệt kê 8.7. Hoàn thành phép nối trên các vector bằng cách thêm các chứng minh viết lại cho append_nil và append_xs (AppendVec.idr)

Danh sách 8.8. Dec: xác định chính xác rằng một thuộc tính là có thể quyết định được.

Danh sách 8.9. Kiểm tra xem Nats có bằng nhau hay không, với kiểu chính xác (CheckEqDec.idr)

Danh sách 8.10. Giao diện DecEq (được định nghĩa trong Prelude)

Danh sách 8.11. Triển khai exactLength sử dụng decEq (ExactLengthDec.idr)

Chương 9. Đại lượng: diễn đạt giả định và hợp đồng trong kiểu dữ liệu

Danh sách 9.1. Kiểu phụ thuộc Elem, biểu thị rằng một giá trị được đảm bảo có trong một vector (được định nghĩa trong Data.Vect)

Danh sách 9.2. Loại bỏ một phần tử khỏi một vector, với một hợp đồng được chỉ định trong loại sử dụng Elem (RemoveElem.idr)

Danh sách 9.3. Định nghĩa removeElem sử dụng tham số tự động (RemoveElem.idr)

Danh sách 9.4. Định nghĩa Elem và isElem bằng tay (ElemType.idr)

Liệt kê 9.5. Định nghĩa hoàn chỉnh của isElem (ElemType.idr)

Danh sách 9.6. Một bài kiểm tra Boolean để xác định xem một giá trị có trong một vector hay không (ElemBool.idr)

Danh sách 9.7. Trạng thái trò chơi (Hangman.idr)

Danh sách 9.8. Xác định chính xác khi nào một trò chơi ở trạng thái hoàn thành (Hangman.idr)

Danh sách 9.9. Hàm trò chơi cấp cao (Hangman.idr)

Danh sách 9.10. Đọc một dự đoán từ bảng điều khiển, đảm bảo rằng nó là hợp lệ (Hangman.idr)

Danh sách 9.11. Loại hàm xử lý dự đoán của người dùng (Hangman.idr)

Danh sách 9.12. Chứng minh rằng một chuỗi đầu vào phải là đầu vào hợp lệ hoặc không hợp lệ (Hangman.idr)

Danh sách 9.13. Hàm trò chơi cấp cao nhất (Hangman.idr)

Danh sách 9.14. Một chương trình chính để thiết lập một trò chơi (Hangman.idr)

Chương 10. Quan điểm: mở rộng khớp mẫu

Danh sách 10.1. Kiểu phụ thuộc ListLast, cung cấp các mẫu thay thế cho một danh sách (DescribeList.idr)

Danh sách 10.2. Mô tả một danh sách dưới dạng ListLast (DescribeList.idr)

Danh sách 10.3. Nỗ lực ban đầu trong việc mergeSort với một mẫu không hợp lệ (MergeSort.idr)

Danh sách 10.4. Một cái nhìn về danh sách cung cấp các mẫu cho danh sách rỗng, danh sách đơn lẻ và kết hợp các danh sách (MergeSort.idr)

Danh sách 10.5. Định nghĩa một hàm bao phủ cho SplitList (MergeSort.idr)

Danh sách 10.6. Kiểu SnocList, tham số hóa trên danh sách tương đương (SnocList.idr)

Liệt kê 10.7. Triển khai hàm bao phủ snocList

Danh sách 10.8. Giao diện SplitRec từ Data.List.Views

Danh sách 10.9. Điểm khởi đầu cho việc triển khai tổng thể của mergeSort, sử dụng SplitRec (MergeSortView.idr)

Danh sách 10.10. Một mô-đun định nghĩa các hình dạng và tính toán diện tích (Shape.idr)

Danh sách 10.11. Xuất Shape dưới dạng kiểu dữ liệu trừu tượng (Shape_abs.idr)

Danh sách 10.12. Cửa hàng dữ liệu, với một lược đồ (DataStore.idr)

Danh sách 10.13. Các hàm để truy cập cửa hàng (DataStore.idr)

Danh sách 10.14. Một giao diện để duyệt qua các mục trong một kho dữ liệu (DataStore.idr)

Danh sách 10.15. Một cơ sở dữ liệu được điền với một số dữ liệu thử nghiệm (TestStore.idr)

Danh sách 10.16. Một hàm để chuyển đổi nội dung của cửa hàng thành danh sách các mục (TestStore.idr)

Chương 11. Dòng dữ liệu và quy trình: làm việc với dữ liệu vô hạn

Danh sách 11.1. Gán nhãn cho từng phần tử của danh sách bằng một số nguyên (Label.idr)

Danh sách 11.2. Một kiểu dữ liệu của các danh sách vô hạn (InfList.idr)

Danh sách 11.3. Kiểu dữ liệu trừu tượng Inf, dùng để trì hoãn các phép toán có thể vô hạn.

Danh sách 11.4. Định nghĩa countFrom như một danh sách vô hạn (InfList.idr)

Danh sách 11.5. Lấy một phần hữu hạn từ một danh sách vô hạn, với Force và Delay ngầm định (InfList.idr)

Danh sách 11.6. Kiểu dữ liệu Stream và một số hàm, được định nghĩa trong Prelude

Danh sách 11.7. Gán nhãn cho từng phần tử của một Danh sách bằng cách sử dụng Stream (Streams.idr)

Danh sách 11.8. Một bài kiểm tra số học, sử dụng một Stream các số cho các câu hỏi (Arith.idr)

Danh sách 11.9. Tạo ra một dòng số ngẫu nhiên giả từ một hạt giống (Arith.idr)

Danh sách 11.10. Tạo đầu vào phù hợp cho bài kiểm tra (Arith.idr)

Danh sách 11.11. Các quá trình tương tác vô hạn (InfIO.idr)

Danh sách 11.12. Một quá trình vô hạn liên tục hiển thị một thông điệp (InfIO.idr)

Danh sách 11.13. Chuyển đổi một biểu thức có kiểu InfIO thành một hành động IO có thể thực thi (InfIO.idr)

Danh sách 11.14. Chuyển đổi một biểu thức của loại InfIO thành một hành động IO có thể thực thi chạy trong thời gian hữu hạn (InfIO.idr)

Danh sách 11.15. Tạo nhiên liệu vô hạn (InfIO.idr)

Danh sách 11.16. Định nghĩa nội bộ của Inf và Lazy

Danh sách 11.17. Định nghĩa cú pháp do cho các chuỗi hành động vô hạn

Danh sách 11.18. Thiết lập InfIO (ArithTotal.idr)

Danh sách 11.19. Định nghĩa một hàm tổng quiz (ArithTotal.idr)

Danh sách 11.20. Hoàn thiện việc triển khai với main (ArithTotal.idr)

Danh sách 11.21. Liên tục chào người dùng, chạy mãi mãi (Greet.idr)

Danh sách 11.22. Kiểu RunIO, mô tả các quá trình có thể vô hạn với một lệnh Quit bổ sung (RunIO.idr)

Danh sách 11.23. Liên tục chào người dùng, thoát khi không có đầu vào (RunIO.idr)

Danh sách 11.24. Chuyển đổi một biểu thức có kiểu RunIO ty thành một hành động có thể thực thi có kiểu IO ty (RunIO.idr)

Danh sách 11.25. Các chương trình tương tác chỉ hỗ trợ I/O console (ArithCmd.idr)

Danh sách 11.26. Thực thi chương trình ConsoleIO (ArithCmd.idr)

Danh sách 11.27. Bài kiểm tra toán, được viết dưới dạng chương trình ConsoleIO (ArithCmd.idr)

Danh sách 11.28. Một hàm chính thực hiện bài kiểm tra và hiển thị điểm số cuối cùng (ArithCmd.idr)

Danh sách 11.29. Tách các thành phần của bài kiểm tra thành các hàm riêng biệt (ArithCmd.idr)

Danh sách 11.30. Định nghĩa một kiểu để đại diện cho đầu vào người dùng, và một lệnh tổng hợp để đọc và phân tích đầu vào (ArithCmdDo.idr)

Danh sách 11.31. Mở rộng Lệnh để cho phép các chuỗi lệnh (ArithCmdDo.idr)

Danh sách 11.32. Tạo hai định nghĩa của (>>=) trong các không gian tên riêng biệt (ArithCmdDo.idr)

Danh sách 11.33. Triển khai readInput bằng lệnh tuần tự (ArithCmdDo.idr)

Danh sách 11.34. Định nghĩa bài kiểm tra sử dụng readInput như một lệnh tổng hợp để hiển thị một thông báo và đọc đầu vào của người dùng (ArithCmdDo.idr)

Chương 12. Viết chương trình với trạng thái

Danh sách 12.1. Gán nhãn cho mỗi phần tử của danh sách bằng cách sử dụng Stream (Streams.idr)

Danh sách 12.2. Định nghĩa về cây nhị phân và một ví dụ (TreeLabel.idr)

Danh sách 12.3. Gắn nhãn một Cây với một luồng nhãn (TreeLabel.idr)

Danh sách 12.4. Trạng thái và các hàm liên quan, được định nghĩa trong Control.Monad.State

Danh sách 12.5. Một hàm có trạng thái tăng giá trị trạng thái theo một giá trị cho trước (State.idr)

Danh sách 12.6. Định nghĩa treeLabelWith như một chuỗi các thao tác có trạng thái (TreeLabelState.idr)

Danh sách 12.7. Hàm cấp cao nhất để gán nhãn cho các nút trong cây, theo thứ tự sâu, từ trái sang phải (TreeLabelState.idr)

Danh sách 12.8. Một kiểu để mô tả các phép toán có trạng thái (TreeLabelType.idr)

Danh sách 12.9. Định nghĩa treeLabelWith như một chuỗi các thao tác có trạng thái (TreeLabelType.idr)

Danh sách 12.10. Chạy một thao tác gán nhãn (TreeLabelType.idr)

Danh sách 12.11. Hàm gán nhãn cây, gọi run với một luồng nhãn khởi đầu (TreeLabelType.idr)

Danh sách 12.12. Sử dụng when và traverse (Traverse.idr)

Danh sách 12.13. Thêm các số nguyên dương từ một danh sách vào một trạng thái (StateMonad.idr)

Danh sách 12.14. Giao diện Monad

Danh sách 12.15. Các giao diện Functor và Applicative

Danh sách 12.16. Triển khai Applicative và Monad cho State (StateMonad.idr)

Danh sách 12.17. Xác định các triển khai Functor, Applicative và Monad cùng nhau (StateMonad.idr)

Danh sách 12.18. Các chương trình tương tác chỉ hỗ trợ I/O console (ArithState.idr)

Danh sách 12.19. Chạy các chương trình tương tác (ArithState.idr)

Danh sách 12.20. Mở rộng kiểu Command để hỗ trợ trạng thái trò chơi (ArithState.idr)

Danh sách 12.21. Đại diện cho trạng thái trò chơi dưới dạng bản ghi lồng nhau (ArithState.idr)

Danh sách 12.22. Hiển thị cài đặt cho GameState (ArithState.idr)

Danh sách 12.23. Thiết lập một trường bản ghi bằng cách so khớp mẫu (ArithState.idr)

Danh sách 12.24. Cài đặt trường bản ghi sử dụng cú pháp cập nhật bản ghi (ArithState.idr)

Danh sách 12.25. Cài đặt các trường bản ghi lồng nhau bằng cú pháp cập nhật bản ghi (ArithState.idr)

Danh sách 12.26. Cập nhật các trường bản ghi lồng bằng cách áp dụng trực tiếp các hàm lên giá trị hiện tại của trường (ArithState.idr)

Danh sách 12.27. Triển khai bài kiểm tra toán (ArithState.idr)

Danh sách 12.28. Xử lý các câu trả lời đúng và sai bằng cách cập nhật trạng thái trò chơi (ArithState.idr)

Danh sách 12.29. Một loại mới và định nghĩa khung cho runCommand (ArithState.idr)

Danh sách 12.30. Định nghĩa hoàn chỉnh của runCommand (ArithState.idr)

Danh sách 12.31. Chạy chương trình ConsoleIO gồm một luồng lệnh (Command) tiềm năng vô tận (ArithState.idr)

Danh sách 12.32. Một chương trình chính khởi tạo bài kiểm tra toán học với một luồng số ngẫu nhiên và một trạng thái ban đầu (ArithState.idr)

Chương 13. Máy trạng thái: xác minh các giao thức trong kiểu dữ liệu

Danh sách 13.1. Đại diện cho các thao tác trên một cánh cửa dưới dạng loại lệnh (Door.idr)

Danh sách 13.2. Mô hình hóa máy trạng thái cửa trong một kiểu, mô tả các chuyển tiếp trạng thái trong các kiểu của các lệnh (Door.idr)

Danh sách 13.3. Mô hình máy bán hàng trong một kiểu, mô tả các chuyển trạng thái trong các kiểu lệnh (Vending.idr)

Danh sách 13.4. Mô hình hoàn chỉnh của trạng thái máy bán hàng (Vending.idr)

Danh sách 13.5. Một vòng lặp chính đọc và xử lý đầu vào của người dùng cho máy bán hàng (Vending.idr)

Danh sách 13.6. Thêm các định nghĩa của vend và refill kiểm tra rằng các điều kiện tiên quyết của chúng được thỏa mãn (Vending.idr)

Danh sách 13.7. Đại diện cho các phép toán trên cấu trúc dữ liệu ngăn xếp với chiều cao đầu vào và đầu ra của ngăn xếp trong loại (Stack.idr)

Danh sách 13.8. Thực hiện một chuỗi hành động trên ngăn xếp, sử dụng Vect để biểu diễn nội dung của ngăn xếp.

Danh sách 13.9. Mở rộng StackCmd để hỗ trợ I/O console với các lệnh GetStr và PutStr (StackIO.idr)

Danh sách 13.10. Cập nhật runStack để hỗ trợ các lệnh tương tác GetStr và PutStr (StackIO.idr)

Danh sách 13.11. Định nghĩa các chuỗi vô hạn của các thao tác ngăn xếp tương tác (StackIO.idr)

Danh sách 13.12. Phác thảo của một máy tính dựa trên ngăn xếp tương tác (StackIO.idr)

Danh sách 13.13. Đọc đầu vào người dùng cho máy tính dựa trên ngăn xếp (StackIO.idr)

Danh sách 13.14. Thêm hai phần tử trên cùng của ngăn xếp, nếu chúng có mặt (StackIO.idr)

Chương 14. Các máy trạng thái phụ thuộc: xử lý phản hồi và lỗi

Liệt kê 14.1. Mô hình hóa máy trạng thái cửa trong một loại

Danh sách 14.2. Kiểu DoorCmd tinh chỉnh, cho phép trạng thái đầu ra của mỗi hoạt động được tính toán từ giá trị trả về của hoạt động (DoorJam.idr)

Danh sách 14.3. Một kiểu để đại diện cho các lệnh của một ATM và cách chúng ảnh hưởng đến trạng thái của ATM (ATM.idr)

Danh sách 14.4. Một hàm atm mô tả một chuỗi các thao tác trên máy ATM (ATM.idr)

Danh sách 14.5. Một triển khai thay thế của atm, bao gồm tin nhắn cho người dùng và kiểm tra PIN sau (ATM.idr)

Danh sách 14.6. Một mô phỏng console của một cây ATM (ATM.idr)

Danh sách 14.7. Bắt đầu định nghĩa GameCmd (Hangman.idr)

Danh sách 14.8. Thêm thao tác Đoán (Hangman.idr)

Danh sách 14.9. Một loại để mô tả các vòng lặp trò chơi có thể vô hạn (Hangman.idr)

Danh sách 14.10. Triển khai hoàn chỉnh của gameLoop (Hangman.idr)

Danh sách 14.11. Đại diện cho trạng thái trò chơi cụ thể (Hangman.idr)

Danh sách 14.12. Một triển khai Show cho Game (Hangman.idr)

Danh sách 14.13. Chạy vòng lặp trò chơi (Hangman.idr)

Liệt kê 14.14. Định nghĩa tóm tắt của runCmd (Hangman.idr)

Chương 15. Lập trình song song an toàn kiểu dữ liệu

Danh sách 15.1. Kênh và PID (được định nghĩa trong System.Concurrency.Channels)

Danh sách 15.2. Phác thảo của một chương trình thiết lập một quá trình cộng (AdderChannel.idr)

Danh sách 15.3. Truyền tin nguyên thủy (được định nghĩa trong System.Concurrency.Channels)

Danh sách 15.4. Định nghĩa hoàn chỉnh của bộ cộng (AdderChannel.idr)

Danh sách 15.5. Định nghĩa hoàn chỉnh của main (AdderChannel.idr)

Danh sách 15.6. Một kiểu để mô tả các quá trình (Process.idr)

Danh sách 15.7. Triển khai một quy trình bộ cộng an toàn kiểu (Process.idr)

Danh sách 15.8. Loại quy trình mới, được mở rộng với Vòng lặp (ProcessLoop.idr)

Danh sách 15.9. Hàm chạy mới, với giới hạn thực thi (ProcessLoop.idr)

Danh sách 15.10. Ghi chú loại Quy trình với các trạng thái đầu vào và đầu ra của nó (ProcessState.idr)

Danh sách 15.11. Các định nghĩa tinh chỉnh của procAdder và procMain (ProcessState.idr)

Danh sách 15.12. Mô tả một giao diện cho các thao tác trên danh sách

Danh sách 15.13. Quá trình tinh chế để bao gồm giao diện của nó trong kiểu, phần 1 (ProcessIFace.idr)

Danh sách 15.14. Quy trình tinh chế để bao gồm giao diện của nó trong kiểu, phần 2 (ProcessIFace.idr)

Danh sách 15.15. Cập nhật chạy cho quy trình đã tinh chỉnh (ProcessIFace.idr)

Danh sách 15.16. Định nghĩa Process trong một module, bỏ qua các định nghĩa (ProcessLib.idr)

Danh sách 15.17. Các loại hàm hỗ trợ cho Process, bỏ qua định nghĩa (ProcessLib.idr)

Danh sách 15.18. Một chương trình chính sử dụng dịch vụ procList (ListProc.idr)

Danh sách 15.19. Một hàm nhỏ để đếm số lượng từ và dòng trong một chuỗi (WordCount.idr)

Danh sách 15.20. Giao diện cho dịch vụ đếm từ (WordCount.idr)

Danh sách 15.21. Sử dụng dịch vụ đếm từ (WordCount.idr)

Danh sách 15.22. Phản hồi các lệnh trong wcService (WordCount.idr)

Danh sách 15.23. Triển khai chưa hoàn chỉnh của wcService (WordCount.idr)

Danh sách 15.24. Tải một tệp và đếm số từ (WordCount.idr)

Type-Driven Development with Idris

Edwin Brady

Copyright

Brief Table of Contents

Table of Contents

Preface

Acknowledgments

About this Book

Who should read this book

Roadmap

Code conventions and downloads

Author Online

Other online resources

About the Author

About the Cover Illustration

Part 1. Introduction

Chapter 1. Overview

Types and tests

1.1. What is a type?

Figure 1.1. The top of a shape-sorter toy. The shapes correspond to the types of objects that will fit through the holes.

1.2. Introducing type-driven development

1.2.1. Matrix arithmetic

Table 1.1. Input and output types for matrix operations. The names x, y, and z describe, in general, how the dimensions of the inputs and outputs are related.

1.2.2. An automated teller machine

Figure 1.2. The states and valid operations on an ATM. Each operation is valid only in specific states and can change the state of the machine. CheckPIN changes the state only if the entered PIN is correct.

State machines and types

1.2.3. Concurrent programming

Figure 1.3. Two interacting concurrent processes, main and adder. The main process sends a request to adder, which then sends a response back to main.

Types versus testing for concurrent programs

1.2.4. Type, define, refine: the process of type-driven development

1.2.5. Dependent types

Table 1.2. Appending specific typed lists. Unlike simple types, where there’s no difference between the input and output list types, dependent types allow the length to be encoded in the type.

Lists and vectors

Table 1.3. Appending typed lists, in general. Type variables describe the relationships between the inputs and outputs, even though the exact inputs and outputs are unknown.

Type variables

Introductory exercises

1.3. Pure functional programming

1.3.1. Purity and referential transparency

Figure 1.4. A pure function, taking inputs and producing outputs with no observable side effects

Figure 1.5. Pure functions, in general, take only inputs and have no observable side effects.

1.3.2. Side-effecting programs

Listing 1.1. Appending lists read from a file (pseudocode)

Figure 1.6. A side-effecting program, reading inputs from a file, printing the result, and returning the result

1.3.3. Partial and total functions

Total functions and long-running programs

1.4. A quick tour of Idris

1.4.1. The interactive environment

Installing Idris

1.4.2. Checking types

1.4.3. Compiling and running Idris programs

Listing 1.2. Hello, Idris World! (Hello.idr)

Whitespace significance

The REPL prompt

1.4.4. Incomplete definitions: working with holes

Listing 1.3. A program with a type error

1.4.5. First-class types

Listing 1.4. Calculating a type, given a Boolean value (FCTypes.idr)

1.5. Summary

Chapter 2. Getting started with Idris

Listing 2.1. A complete Idris program to calculate average word length (Average.idr)

2.1. Basic types

The Prelude

2.1.1. Numeric types and values

Subtraction with Nats

“the” expressions

2.1.2. Type conversions using cast

2.1.3. Characters and strings

Function syntax

2.1.4. Booleans

Inequality

2.2. Functions: the building blocks of Idris programs

2.2.1. Function types and definitions

Listing 2.2. A function to double an Int (Double.idr)

Figure 2.1. The components of a function definition

Type declarations are required!

2.2.2. Partially applying functions

2.2.3. Writing generic functions: variables in types

The id function

Variable names in types

2.2.4. Writing generic functions with constrained types

Part 1.
Introduction

Chapter 1.
Overview

Figure 1.1.
The top of a shape-sorter toy. The shapes correspond to the types of objects that will fit through the holes.

1.2.1.
Matrix arithmetic

Table 1.1.
Input and output types for matrix operations. The names `x`, `y`, and `z` describe, in general, how the dimensions of the inputs and outputs are related.

1.2.2.
An automated teller machine

Figure 1.2.
The states and valid operations on an ATM. Each operation is valid only in specific states and can change the state of the machine. `CheckPIN` changes the state only if the entered PIN is correct.

1.2.3.
Concurrent programming

Figure 1.3.
Two interacting concurrent processes, `main` and `adder`. The `main` process sends a request to `adder`, which then sends a response back to `main`.

1.2.4.
Type, define, refine: the process of type-driven development

1.2.5.
Dependent types

Table 1.2.
Appending specific typed lists. Unlike simple types, where there’s no difference between the input and output list types, dependent types allow the length to be encoded in the type.

Table 1.3.
Appending typed lists, in general. Type variables describe the relationships between the inputs and outputs, even though the exact inputs and outputs are unknown.

1.3.1.
Purity and referential transparency

Figure 1.4.
A pure function, taking inputs and producing outputs with no observable side effects

Figure 1.5.
Pure functions, in general, take only inputs and have no observable side effects.

1.3.2.
Side-effecting programs

Listing 1.1.
Appending lists read from a file (pseudocode)

Figure 1.6.
A side-effecting program, reading inputs from a file, printing the result, and returning the result

1.3.3.
Partial and total functions

1.4.1.
The interactive environment

1.4.2.
Checking types

1.4.3.
Compiling and running Idris programs

Listing 1.2.
Hello, Idris World! (Hello.idr)

1.4.4.
Incomplete definitions: working with holes

Listing 1.3.
A program with a type error

1.4.5.
First-class types

Listing 1.4.
Calculating a type, given a Boolean value (FCTypes.idr)

Chapter 2.
Getting started with Idris

Listing 2.1.
A complete Idris program to calculate average word length (Average.idr)

2.1.1.
Numeric types and values

2.1.2.
Type conversions using cast

2.1.3.
Characters and strings

2.1.4.
Booleans

2.2.1.
Function types and definitions

Listing 2.2.
A function to double an `Int` (Double.idr)

Figure 2.1.
The components of a function definition

2.2.2.
Partially applying functions

2.2.3.
Writing generic functions: variables in types

2.2.4.
Writing generic functions with constrained types

Listing 2.3.
A generic type, constrained to numeric types (Generic.idr)

2.2.5.
Higher-order function types

Listing 2.4.
Defining `quadruple` and `rotate` using a higher-order function (HOF.idr)

2.2.6.
Anonymous functions

2.2.7.
Local definitions: let and where

Figure 2.2.
A local variable definition: in the expression after the `in` keyword, `x` has the value `50`.

Listing 2.5.
Local variables with `let` (Let_Where.idr)

Listing 2.6.
Local function definitions with `where` (Let_Where.idr)

2.3.1.
Tuples

2.3.2.
Lists

2.3.3.
Functions with lists

Listing 2.7.
Calculating the average word length in a string (Average.idr)

2.4.1.
Whitespace significance: the layout rule

Listing 2.8.
The layout rule applied to `average` (Average.idr)

Listing 2.9.
The layout rule, applied incorrectly

2.4.2.
Documentation comments

2.4.3.
Interactive programs

Listing 2.10.
Reversing strings interactively (Reverse.idr)

Listing 2.11.
Displaying average word lengths interactively (AveMain.idr)

Part 2.
Core Idris

Chapter 3.
Interactive development with types

3.1.1.
Interactive command summary

Table 3.1.
Interactive editing commands in Atom

3.1.2.
Defining functions by pattern matching

Figure 3.1.
Matching the pattern `(x :: xs)` for inputs `[1]` and `[2,3,4,5]`

Listing 3.1.
Calculating word lengths by pattern matching on the list (WordLength.idr)

3.1.3.
Data types and patterns

Listing 3.2.
Vectors: lists with lengths encoded in the type (Vectors.idr)

3.2.1.
Refining the type of allLengths

Figure 3.2.
Calculating the lengths of words in a list. Notice that each input has a corresponding output, so the length of the output vector is always the same as the length of the input vector.

3.2.2.
Type-directed search: automatic refining

3.2.3.
Type, define, refine: sorting a vector

Listing 3.3.
A skeleton definition of `insSort` on vectors with an initial type (VecSort.idr)

Figure 3.3.
Representation of a matrix as two-dimensional vectors. On the left, the matrix is in mathematical notation. The same matrix is represented in Idris on the right.

3.3.1.
Matrix operations and their types

3.3.2.
Transposing a matrix

Figure 3.4.
The components of the vector you’re transposing (`x` and `xs`), along with the result of transposing `xs`, and the expected overall result

Listing 3.4.
Complete definition of matrix transposition (Matrix.idr)

3.4.1.
The need for implicit arguments

3.4.2.
Bound and unbound implicits